一种交通噪声预测概率统计分析模型

汪小黎

(商洛学院,数学与计算机应用学院， 陕西，商洛 726000)

0 引言

道路交通的发展给人们的生活带来诸多便利，然而也给城市带来了严重的噪声污染[1-2]。准确的交通噪声预测是交通噪声控制的前提，也是环境管理的重要任务。

目前流行的交通噪声预测模型有2种：稳态计算模型[3]和动态仿真模型[4-6]。稳态计算模型可以根据一段时间内的平均交通量、平均车速等来预测一段时间内的平均交通噪声。虽然稳态计算模型能预测一段时间内的等效噪声级或时间平均噪声级，然而无法计算噪声的动态变化。

动态仿真模型不仅可用于预测一段时间内的等效声级，还可用于预测噪声级的逐秒动态变化。此外，该方法通常通过结合动态交通仿真模型、车辆噪声排放模型和声音传播模型来工作。随着计算机技术的发展，动态仿真模型在交通噪声预测中的应用越来越广泛。李锋等[5]对环形交叉口的实时交通流进行动态模拟，再结合单辆机动车的噪声排放模型以及传播衰减模型，计算得到环形交叉口的交通噪声。王超等[6]对斜坡道路进行噪声动态模拟，并给出了高架斜坡道路的声场分布规律。李晓等[7]提出了以车流密度为变量的噪声源动态声源辐射计算模型。付乐宜等[8]以Web端Mapbox为展示平台，基于交通噪声模型和GPS轨迹数据，实现噪声数据的立体动态化显示。动态仿真模型计算复杂。而且，在动态仿真模型中，几乎所有的车辆噪声排放模型都是与车速和车型相关的固定代数表达式，这使得在实际情况下很难表示各种噪声排放。

为了简化交通流模拟的过程，保持预测参数的多样性和准确性，本文基于蒙特卡罗方法设计了交通流模型，并提出了一种基于车辆噪声排放概率分布模型的交通噪声预测方法。

1 模型介绍

1.1 自由流道路模型

如图1所示，当汽车在道路上行驶时接收点的声压级可以表示为

图1 自由流道路模型示意图

Lj=Lj,0+Lj,D+Lj,other

(1)

式中，Lj,0表示在标准距离处测得的单个车辆的声压级，可视为单个车辆的发射噪声,Lj,D表示距离衰减,Lj,other表示其他因素引起的噪声衰减，如空气吸收和屏障屏蔽等。

一般情况下，Lj,0表示为在标准距离d0=7.5 m处测量的单个车辆声压级。然而，不同车辆的噪声排放不是固定的，且在一定的分布范围内波动。因此，本文假设每种车辆在每一特定速度范围内的噪声排放服从一定的分布，其概率密度函数可以表示为

y=f(Lj,0)

(2)

通过对大量试验数据的分析，将车辆按重量分为若干种类型，并将每种类型的车辆进一步分为若干速度等级，得到概率密度函数f(Lj,0)。

距离衰减可以表示为

(3)

式中，d0表示测量单车噪声排放时的参考距离，通常情况取7.5 m,d表示车辆到接收点的距离，通常取决于车辆在道路上的坐标(用x表示)和从接收点到道路的垂直距离(用r表示)。假设影响接收点的道路长度为l(m)，x在l范围内服从均匀分布，其概率密度函数定义如，

(4)

为排除研究路段外车辆的影响，建议接收点与路段的视角大于150，且l的值为400 m。

将道路上的交通流分为两个方向，通过将方向1内车辆的所有声功率相加，计算方向1在任何时刻产生的噪声，计算公式为

(5)

其中,m表示道路上的车辆数量。在直线道路上自由流动的情况下，m服从泊松分布，其概率密度函数定义为

(6)

式中，k是道路上的平均车辆数，且与每小时交通量Q和速度v(m/s)有关，具体定义为

(7)

方向2在任何时刻(Li,2)产生的噪声可以使用相同的方法计算。然后，将两个方向的声功率相加即可得到瞬时声级，

Li=10lg(100.1·Li,1+100.1·Li,2)

(8)

1.2 控制流道路模型

对于控制流道路，本文通过停车线将车道分为两段，l1和l2(m)。同样地，为了确保接收点与路段的视角大于150，建议l1和l2为200 m。交通灯控制下的车辆运行过程如图2所示。假设交通信号灯的信号周期为T，红灯时间和绿灯时间分别为TR和TG，T表示从红灯亮起信号周期的第t次。因此，t在(0,T)范围内服从均匀分布。在任何时期的第t秒，控制流道路模型总结如下。

图2 控制流道路模型示意图

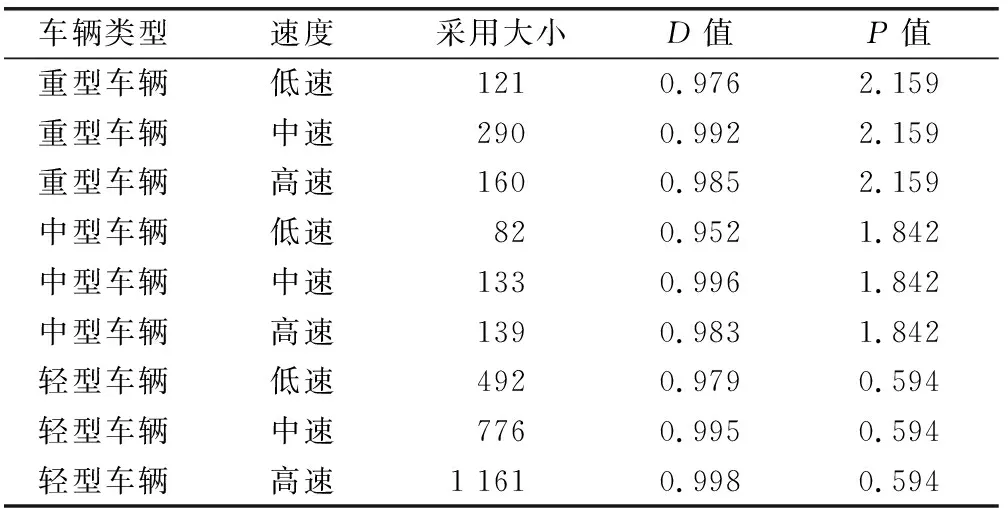
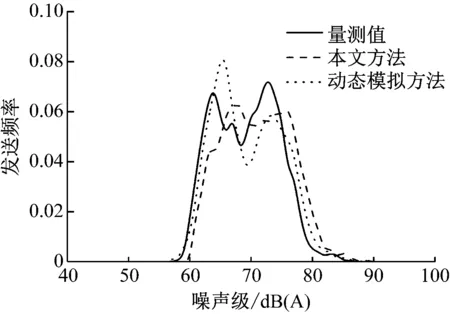
当交通灯为红色(0

匀分布，且ls表示平均车头时距。目前，上一次绿灯放行的排队头车行驶了TG+t(s)，尾车行驶了t(s)。因此，l2内的车辆数m2,R更新为

(9)

式中，ht表示交通流的平均车头时距，即队列中2个连续车辆之间的时间间隔,V表示离开交通流的平均速度,l2/V表示车辆离开l2所需的时间。类似地，lx,2在(Vt,l2)范围内服从均匀分布。

当交通灯为绿色(TR

(10)

式中，m1,t服从泊松分布，即λ=Qt/3 600。lx1在(-m1,G·ls,0)范围内服从均匀分布。此时l2内的车辆数m2,G存在为两种情况：①当t-TT

(11)

1.3 噪声排放模型

本节选择交通量小、100 m左右无明显反光的直线道路作为实验场景。声级计设置在距离地面1.2 m，距离道路两侧行车道7.5 m。车辆分为三类：长度小于6 m，重量小于2 t的轻型车辆；长度大于10 m或重量大于12 t的重型车辆；中型车辆，即除轻型车辆或重型车辆以外的任何车辆。对3 300辆汽车(包括2 429辆轻型车、354辆中型车和517辆重型车)通过声级计时的噪声排放进行了测量。每辆车的速度都被雷达测速仪记录下来。

此外，车辆的速度分为3个等级：低速(0-20 km/h)、中速(20-50 km/h)和高速(50 km/h以上)。进一步，对各车速等级各车型的噪声排放进行正态性检验[9]，如表1所示。正态性检验的结果表明，各组噪声排放数据的显著性水平均大于0.05。虽然少数几组数据的显著性水平相对较低(如低速重型车辆和高速中型车辆)，数据近似服从正态分布。因此，式(2)(Lj,0的概率密度函数)可以表示为

表1 车辆噪声排放正态性检验统计结果

(12)

2 模型计算

本节假定任何给定时刻的交通噪声可通过蒙特卡罗方法[10]进行模拟。根据不同道路情况，可将交通噪声分为两种来源：其一为自由流道路模型；其二为控制流道路模型。各模型具体介绍如下。

2.1 自由流道路模型

步骤1：生成一个表示车辆数量的随机数m，且服从泊松分布(式(6))；

步骤2：根据每个参数的概率分布，随机生成m组车辆参数(表示m辆车，如车型、坐标、速度等)；

步骤3：重复步骤1和步骤2，为其他方向行驶的车辆生成参数；

步骤4：根据第2步产生的速度和噪声排放模型，随机生成每辆车的噪声排放值。同时，计算每辆车在接收点产生的噪声级(式(3))。最后，将所有车辆的噪声功率相加，得到给定时刻所有车辆的噪声级；

步骤5：重复上述计算N次，得到N个瞬时噪声级；

步骤6：计算等效连续声级Leq、统计声级L10、L50和L90，以及这些瞬时噪声级的一段时间内交通噪声的概率分布。

2.2 控制流道路模型

步骤1：生成一个随机数t，表示均匀分布t～U[0,T]之后的第t个信号周期；

步骤2：生成车辆数量随机数m1,R，m2,R或m1,G，m2,G；

其余步骤与自由流道路的步骤相同。

3 模型验证

本节选取重庆市自由流道路(菜袁路)和控制流道路(中兴路)进行了模型验证的现场测量。噪音水平由声级计记录，声级计安装在离路边5 m、离地1.2 m处。对于典型的控制流道路，声级计同时设置在停车线下游10 m、30 m和50 m处。通过摄像机记录同时的交通流量，并计算轻型、中型和重型车辆的双向交通量。此外，利用雷达测速仪记录车速，得到道路的速度分布。测量了道路宽度、车道数等几何参数。同时,记录红绿灯时间和红绿灯周期。对大约四分之一的车辆速度进行了测量与统计分析。实验过程均由作者本人独立完成。测试过程中所使用的实验设备部分参数如表2所示。

表2 实验设备部分参数

图3为自由流道路上，车速主要集中在40～70 km/h；图4为控制流道路上，车速分为停车线前减速流和停车线后加速流两种情况。减速流的速度分布比加速流宽。原因是车流比较少，所以有些车辆需要在停车线前减速，有些车辆不需要减速但可以直接通过。

图3 自由流道路统计分析

图4 控制流道路统计分析

表3为各调查道路的交通量和速度水平情况。应注意的是，对于控制流道路，表3仅给出了车辆进出交叉口时测量速度的分布，当车辆即将停止或刚开始运行时的速度被归类为“低速”(表3中未反映出这一点，但在计算中予以考虑)。

表3 实验测试统计情况

进一步将实测交通量、车速概率分布、车型概率分布、道路几何参数等交通参数代入模型。同时，计算每秒钟的随机瞬时噪声级，对噪声水平值进行概率分布统计，并将结果与动态交通噪声模拟方法给出的结果以及实测结果进行对比。图5和图6分别显示了自由流道路和控制流道路在1 h内收集的噪声级值的概率分布。可以看出，动态模拟方法因噪声发射规律比较单一，具有弱离散性，使得声级分布更集中于某些区域，峰值更高；本文所提模型的结果更随机，更加符合实际情况。此外，两种方法的结果显示自由流道路附近的噪声级呈“单峰”分布，而控制流道路附近的噪声级呈“双峰”分布。分析其原因是交通流在红绿灯控制下不连续，绿灯时的交通噪声水平明显高于红灯时。

图5 自由流道路噪声级概率分布

图6 控制流道路噪声级概率分布

4 总结

解决交通噪声是环境管理的关键任务之一。然而针对交通噪声的模拟数据与实测数据存在一定的误差，这将进一步影响交通噪声级概率分布预测的结果。为此，本文对基于蒙特卡罗方法的交通流模型进行了研究，提出了自由流与控制率交通模型，并根据模型对道路交通噪声进行了预测。