电力行业景气分析指标体系构建与景气指数趋势预测

彭放， 刘化龙， 李博

(1.国网电网有限公司大数据中心， 北京 100052； 2.国网信通亿力科技有限责任公司， 福建， 福州 350003)

0 引言

电力行业的发展是经济增长的有力支撑，可以说电力行业是国民经济的晴雨表、经济建设的先行者，然而与此同时我们也需要明确认识到经济高速增长是不可持续的。近年来，面临产能过剩、结构失衡等诸多难题，电力消费与经济发展密切相关，从对电力数据的分析结果中可以判断出经济形势走向。因此，本文对电力行业的景气指数进行深入研究，力求通过科学手段对未来发展趋势进行预测，为整体宏观调控奠定理论基础。

1 景气分析总体概述

1.1 基础概念

景气分析是一种经济周期统计分析方法，在经济研究的各个领域都有应用，在各行各业的企业运营过程中，经常出现经济波动现象，研究这种周期性增长与缩减、扩张与萎缩的经济波动现象的方法称为景气分析法。

1.2 发展现状

景气分析研究已有近一百多年的发展历史，纵观整体发展历程，理论体系已经相对完善，而且已经应用于各行各业的行业分析以及监测预警，是很多国家监测经济发展的重要方法。目前国内外的研究方法主要包括KL信息量法、主成分分析法、时差相关系统法等[1]。

1.3 分析理论与指标划分

景气分析是一种经济周期统计方法，根据指标在时序上的差异，按先后顺序将指标划分为先行指标、一致指标、滞后指标3大类，以此构成分析体系。其中，先行指标指的是循环波动比景气循环转折提前显示变动的指标；一致指标指的是循环转折变化的时间与景气循环转折基本接近的指标；滞后指标指的是比景气循环转折出现的要晚的指标。由此计算得出景气扩展指数(DI)与景气合成指数(CI)，可体现经济景气的增长或衰减趋势、强弱变化。

一般来说，研究景气的基准指标选取的是国内生产总值，循环选取的是增长周期的波动循环。得到基准指标之后，根据时差分析选择先行指标与滞后指标，各分类的作用与划分规则如表1所示。

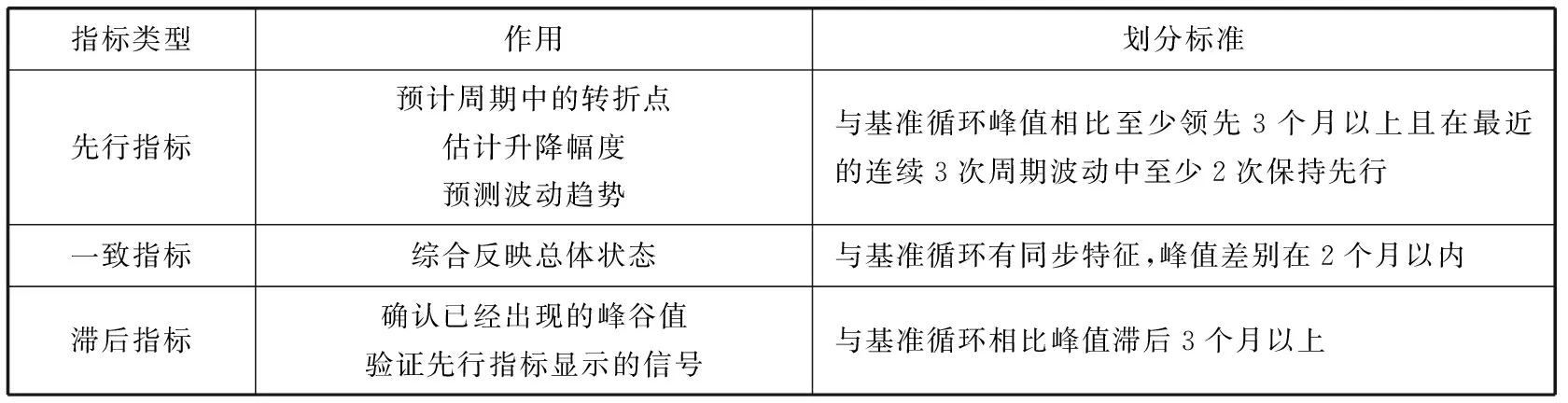
表1 景气指标分类

1.4 指标选取原则

影响行业景气波动的因素有很多，既包括行业本身生产活动的影响，也包括上下游及相关联的其他产业的影响，还包括国家政策、国际局势等等具有随机性的因素，所以在选取景气指标时，应遵循以下原则。

(1) 全面：不能只强调某一片面的指标，需要全方位多维度进行分析评价。

(2) 灵敏：无论是先行指标还是一致指标、滞后指标，选择时特征一定要明显。

(3) 及时：景气分析的指标数据时效性一定要高，否则无法达到预测目的。

(4) 准确：准确是分析的基本保障，否则全部分析都失去意义[2]。

2 数据预处理

2.1 数据补充

电力行业的源数据多种多样，基于目前的信息化采集手段，难免会有部分缺失，对于残缺的数据需要根据数据量的多少利用不同的值进行替代与补充，同时对于补充的数据做敏感性分析，避免个别指标错误导致影响整个分析体系。本文采用的方法如下。

1) 缺失数据补充

(1) 少量缺失：利用前后时期的均值进行替代补充

(1)

(2) 大量数据缺失：利用已有数据与全国数据的占比的平均值与全国数据相乘来替代补充

(2)

(3) 全部缺失又重要的数据：利用全国数据进行替代。

2) 敏感性分析

(1) 回归计算：对包含与不包含插入值的2个序列进行回归计算

(3)

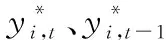
(2) 敏感系数计算：

(4)

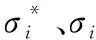
综上所述，若敏感系统在0.8到1.2之间，则认为所补缺失值合理，否则按1%递增或递减，直到达到目标范围。

2.2 标准化处理

为消除量纲的影响，将指标归一化为同向指标，本文采用功效系统法对数据做标准化，将各项指标最小值设为60，最大值设为100。最终值越大越景气的为正向指标，值越小越不景气的为逆向指标，其功效化公式为

(5)

其中，yit为第i个指标t季度的数值。

3 关键算法

3.1 Census X-12法季节调整

为识别和预估时间序列的不同组成部分，了解走向趋势与业务周期，需要做季节性调整，剔除季节和特定日期对最终分析的影响，科学把握宏观经济形势。本文采用Census X-12方法进行季节调整，设YT代表无奇异值的季度时间序列，可分解为趋势循环项、季节项和随机要素项[3]。具体步骤如下。

(1) 初始估计

趋势循环项初始估计：

(6)

随机要素项初始估计：

(7)

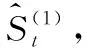
(8)

其中，

(9)

(10)

(2) 计算趋势循环要素与季节因子估计值

利用Henderson移动平均公式计算暂定值：

(11)

(12)

通过3*5项移动平均计算暂定S值

(13)

得到第二次预估的季节调整结果：

(14)

其中，

(15)

(3) 计算趋势循环要素与季节因子最终值

根据上述步骤获得最终值

(16)

其中，

(17)

3.2 Kalman滤波算法

本文基于Kalman滤波法对空间模型进行估计，具体步骤如下。

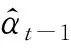
(18)

假设初始状态向量与扰动项服从正态分布，估计误差的协方差矩阵为

(19)

最终得出

(20)

4 电力行业景气指数研究

4.1 指标体系

电力行业景气指数指标体系的构建，首先要考虑电力行业本身的指标，包括总量、当前结构、发展潜能、用电价格等多方面，其次还需要考虑石油、煤炭等上游产业的影响，另外还需要对水泥、化纤等下游产业进行关联的分析，因此本文选取其中的关键因素构建电力行业的景气指标体系如表2所示。

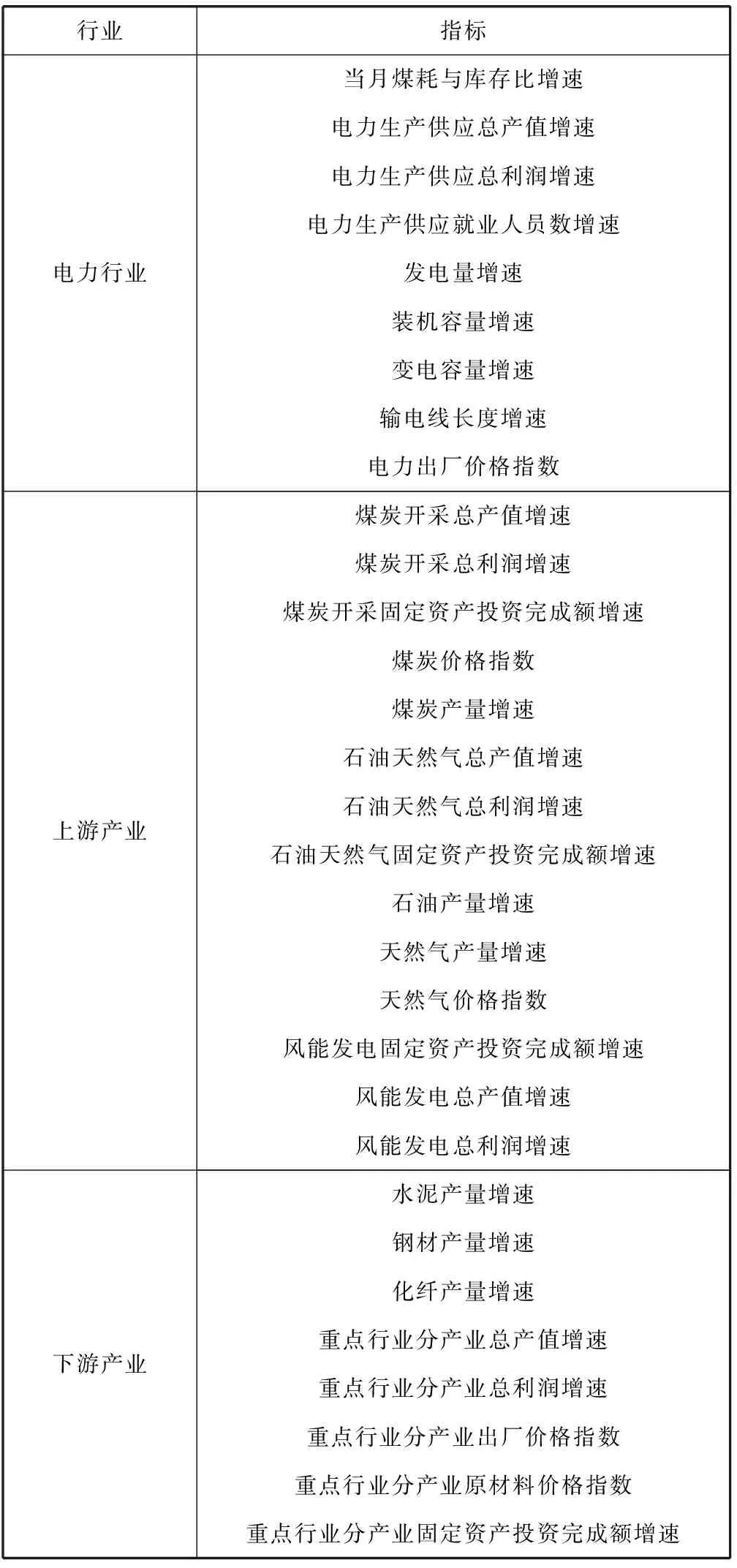
表2 电力行业景气分析指标体系

4.2 模型构建

设yt为k*1维向量，代表t时期可观测的变量，平稳部分，ct为标量，代表t时期景气指数真值，c为不可观测的景气指数，则

yt=h(ct)+utt=1,…,Tc=c1,c2,…,cT

(21)

将ct,ut看做随机过程，对不可观测的ct进行估计，得到

(22)

其中，L为延迟算子，

Θi=diag(θi1,…,θik);H=diag(h1,…,hk);

LCt=ct-1,Lut=ut-1

(23)

根据状态变量αt=(ct,ct-1,…,ct-p+1,ut,ut-r+1)(p+kr)×1；干扰项ξt=(ht,0,…,0,εt,0,…,0)(p+kr)×1;∑=diag(1,0p-1,h1,h2,…,hk,0(k-1)r)

得到目标值：

(24)

其中，Ik为k×k单位阵，0k,k为k×k阶零矩阵。

4.3 测算流程

电力行业景气指数需要准确反映出行业的整体运行情况以及未来发展趋势，基于指数模型体系，通过残缺值替代补充、敏感性分析、标准化处理、季节调整等变换后，根据指标的历史波动幅度对不同区域进行测算打分，最终得到综合评分[4-5]。测算流程如图1所示。

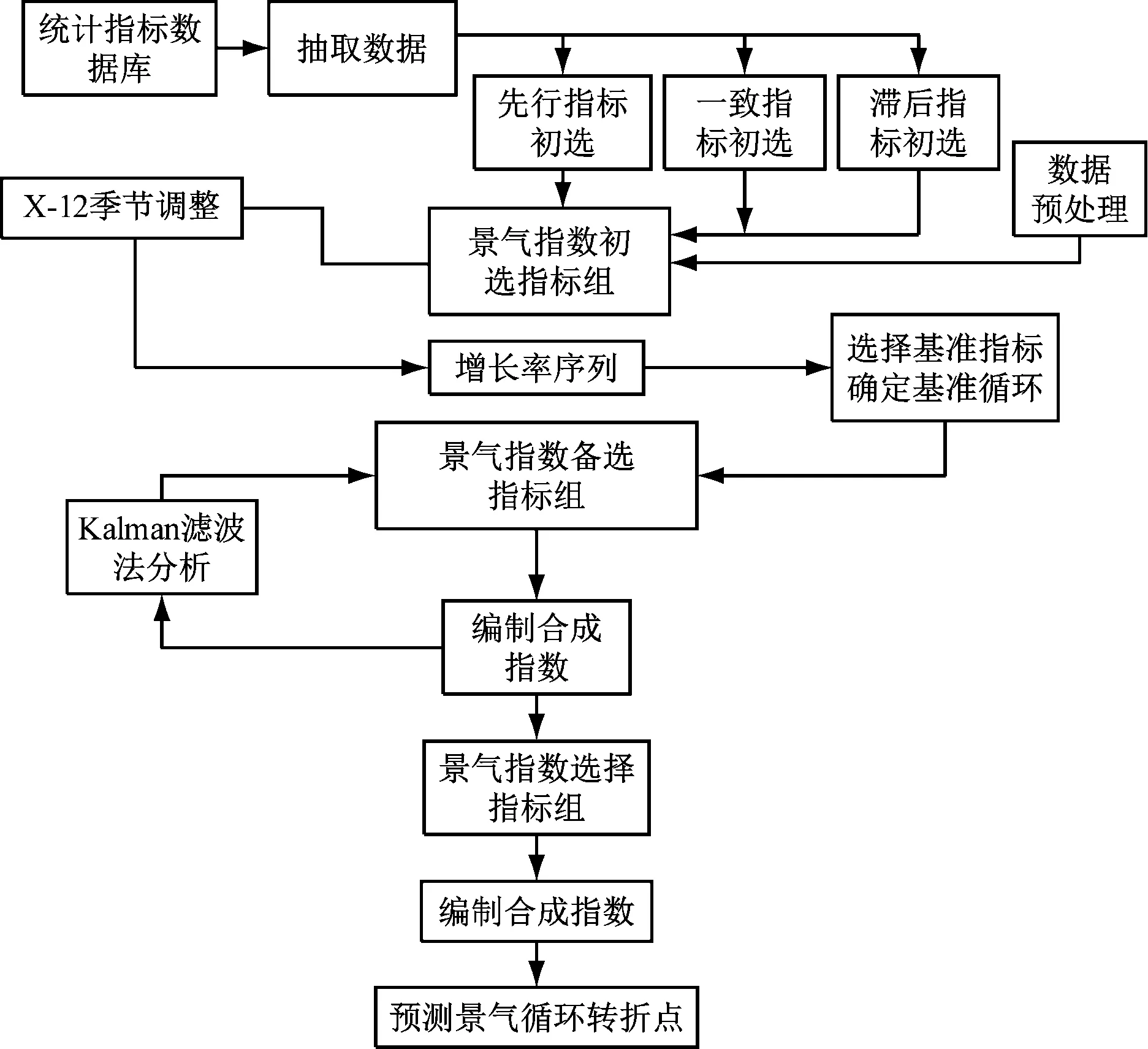
图1 电力行业景气指数测算流程

5 预测结果验证

基于本文上述构建的指标体系与模型，对电力行业景气指数与宏观经济景气指数进行验证，结果表明从2013年到2019年，大致有2个完整的循环，第二个周期的波动程度略低，2019年以前电力行业景气指数大约提前1～2个月，而2019年之后则有滞后1～2个月的趋势，可以预测未来的周期波动逐渐趋于缓慢。由此可以证明，本文构建的电力行业景气指数可以较好的体现未来的发展趋势[6]。

6 总结

不同时期会产生不同的波动规律，本文构建了电力行业的景气指数，通过科学算法来对发展趋势进行预估与判断。虽然指标体系已经初步建立，还还存在很大不足之处，例如数据筛选方法的科学合理性、选取数据范围、指标选取合理性等方面还需继续研究与改善。