基于大数据分析技术的高校毕业就业预测模型

李沛林

(云南省互联网应急中心， 云南，昆明 650011)

0 引言

随着高校不断的扩招，高校毕业生人数在不断增加，毕业生的就业竞争越来越激烈，社会就业压力增大，毕业生就业情况直接关系社会的稳定[1]。一般高校都有相应的毕业生就业管理系统，系统中全面保存学生的就业信息，可以对这些信息进行分析，找到影响高校毕业生就业的因素，并给高校就业工作者提供有价值的参考信息和建议，而高校毕业生就业预测就是一个重要的研究方向[2-4]。

对于高校毕业生就业预测问题，许多学者做了各种尝试，当前存在许多有效的高校毕业生就业预测方法。如有学者提出了基于灰色理论的高校毕业生就业预测方法[5-6]，该方法将高校毕业生就业问题看作一个灰色问题，通过拟合输入和输出之间的关系，进行高校毕业生就业预测，该方法简单，建模效率高，但是由于其简化了高校毕业生就业预测问题，因此高校毕业生就业预测结果不可靠[7]。随后出现了基于神经网络的高校毕业生就业预测方法，通过模拟人类大脑神经网络的工作原理进行建模[8-9]，但是人工神经网络需要问题的先验知识，缺陷十分明显，如高校毕业生就业预测建模过于复杂，高校毕业生就业预测误差大等[10]。近几年，出现了基于支持向量机的高校毕业生就业方法[11]，该方法不存在神经网络的缺陷，高校毕业生就业预测效果得到了改善，但是其高校毕业生就业预测建模时间长，效率极低，无法适应当前高校毕业生就业发展要求[12]。

为了获得更高精度的高校毕业生就业预测结果，本文提出了基于大数据分析技术的高校毕业生就业预测模型(ACO-LSSVM)。首先收集高校毕业生就业相关样本数据，将其输入到大数据分析技术—支持向量机进行训练，拟合高校毕业生就业变化态势，然后采用蚁群算法根据高校毕业生就业变化态势对预测模型参数进行优化，构建最优的高校毕业生就业预测模型，最后与其它高校毕业生就业预测模型进行了对比测试，结果表明，大数据分析技术可以更好的描述高校毕业生就业变化态势，提升高校毕业生预测效果，加快高校毕业生就业预测速度，具有更高的实际应用价值。

1 基于大数据分析技术的高校毕业生就业预测方法具体设计

1.1 高校毕业生就业预测问题描述

高校毕业生就业是一个系统工程，其与多种因素相关，如高校本身的名气、学生专业、当前经济、学生本身的学习情况、学生对毕业单位的期望等，具有较强的时变性、多样性，这给高校毕业生就业预测带来一定的困难。高校毕业生就业预测问题本质就是通过一定的方法对影响因素和高校毕业生就业率之间的变化关系进行拟合，找到高校毕业生就业变化特点，根据该特点对将来高校毕业生就业变化趋势进行预测。设一个高校毕业生就业历史数据为x1,x2,…,xn，y表示将来的高校毕业生就业结果，那么高校毕业生就业预测问题可表示为

y=f(x1,x2,…,xn)

(1)

式中，f()为输入和输出之间关系的拟合函数。

为了更好的对高校毕业生就业输入和输出之间关系进行拟合，本文引入大数据分析技术中的最小二乘支持向量机对拟合函数进行建模，并引入蚁群算法确定最小二乘支持向量机参数的最优值。

1.2 大数据分析技术

最小二乘支持向量机是一种针对非线性预测问题的大数据分析技术，相对于传统支持向量机，其继承了支持向量机的优点，同时进行了一些改进，如：将损失函数变为最小二乘损失函数，不等式约束变为等式约束，优化了耗时的二次规划问题，复杂度明显减少，同时提高了求解的速度。

对于训练集：D={(xi,yi),i=1,2,…,n}，通过映射函数φ(xi)将xi∈Rd变换到高维特征空间，建立如下回归函数

f(x)=ω·φ(x)+b

(2)

式中，ω和b分别表示权向量和偏移量。

最小二乘支持向量机采用误差平方ξi作为损失函数，这样最小二乘支持向量机优化问题变为

(3)

式中，C为正则化参数且表示对超出误差范围样本的惩罚度。

引入拉格朗函数对式(3)进行求解，拉格朗函数定义如下

(4)

式中，ai表示拉格朗乘子。

最优解满足Karush-Kuhn-Tucker条件得到

(5)

同解变换后消除ω和ξi得到矩阵形式为

(6)

式中

(7)

(8)

式中，k(xi,x)具体为

(9)

式中，σ为核宽度参数。

1.3 蚁群算法最小二乘支持向量机参数

核宽度参数σ和正则化参数C影响最小二乘支持向量机的学习效果，传统方法采用人工方式随机确定或者粒子群算法确定，但是它们都存在不足，本文采用蚁群算法确定核宽度参数σ和正则化参数C的最优值，具体过程如下。

(1) 随机产生多个蚂蚁，每一个蚂蚁部署在初始节点。

(2) 对于第i只蚂蚁，计算其从节点i转到节点j的转移概率，具体计算为

(10)

(3) 每一只蚂蚁完成一次搜索后，对其经过的路径上的信息素进行更新，具体如下

(11)

(4) 增加迭代次数，如果小于最大迭代次数，返回步骤(2)继续进行，直到大于最大迭代次数为止。

(5) 将蚂蚁所经过的节点连续起来，组成一个路径，这样得到多条路径。

(6) 选择最短路径为蚁群算法的搜索结果，并对最优路径进行解码，得到参数σ和C的最优值。

1.4 基于大数据分析技术的高校毕业生就业预测建模步骤

Step1：对于某一个高校毕业生，对它们就业信息进行分析，提取与预测相关的数据。

Step2：对就业数据进行处理，剔除其中错误或者无效的数据，并划分为训练集和测试集。

Step3：采用最小二乘支持向量机对高校毕业生就业的训练集进行学习，利用蚁群算法确定核宽度参数和正则化参数的最优值。

Step4：根据核宽度参数和正则化参数的最优值建立高校毕业生就业预测模型，如图1所示。

图1 大数据分析技术的高校毕业生就业预测过程

2 仿真实验

2.1 对比方法和测试数据

为了分析大数据分析技术的高校毕业生就业预测效果，采用VC ++6.0编程实现仿真实验，并对仿真实验测试结果进行分析。为了使大数据分析技术的高校毕业生就业预测结果具有可比性，选择2种高校毕业生就业预测方法在相同仿真环境下进行对比测试，对比方法设计如下

(1) 最小二乘支持向量机的参数凭经验采用随机方式设置，该高校毕业生就业预测方法称之为LSSVM。

(2) 最小二乘支持向量机的参数通过粒子群算法设置，该高校毕业生就业预测方法称之为PSO-LSSVM。

由于高校的类型很多，本文基于国家对高校的分类情况，将高校划分为：985大学，211大学，一本大学，二本学院，高等职业技术学院，对每一种高校，选择不同数量的毕业生就业数据作为研究对象，它们数量具体分布表1所示。

表1 测试对象数据的分布

2.2 设置高校毕业生就业预测方法的参数

采用随机方式设置最小二乘支持向量机的参数，具体如表2所示。同时采用粒子群算法、蚁群算法在线优化最小二乘支持向量机的参数，根据高校毕业生就业预测误差最小化为目标，通过不断的迭代得到的参数最优值如表2所示。对表2的最小二乘支持向量机参数值进行分析可以发现，3种高校毕业生就业预测方法的参数不同，建立了不同的高校毕业生就业预测预测模型。

表2 高校毕业生就业预测方法的参数值

2.3 高校毕业生就业预测效果对比

采用高校毕业生就业预测精度和误差衡量不同方法的性能，对于每一类高校毕业生就业预测数据，随机选择1/2数据组成训练集，用于设计高校毕业生就业预测模型，其它数据对模型的性能进行分析，不同方法预测效果见图2和图3。从预测效果可以发现

图2 预测精度对比

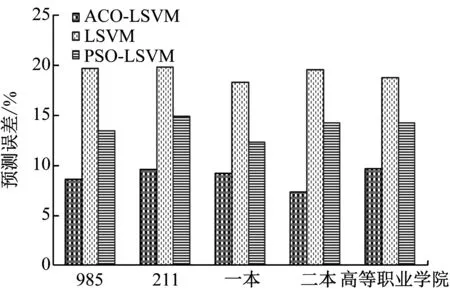
图3 预测误差对比

(1) 平均预测精度最低方法为LSSVM，其高校毕业生就业预测误差最高，这是因为随机确定参数难以建立理想的高校毕业生就业预测模型，无法描述高校毕业生就业变化特点。

(2) PSO-LSSVM的预测效果要明显优于LSSVM，这说明采用粒子群算法获得的参数要优于随机确定的参数，可以描述高校毕业生就业变化特点，提高了高校毕业生就业平均预测精度。

(3) 在本文所有方法中，ACO-LSSVM的高校毕业生就业预测效果最好，提升了高校毕业生就业平均预测精度，误差控制在高校毕业生就业实际要求范围内，获得了理想的高校毕业生就业预测结果，验证了ACO-LSSVM应用于高校毕业生就业预测中的优越性。

2.4 高校毕业生就业预测效果对比

由于当前高校毕业生数量比较大，因此对于建模方法的效率要求也越来越高，分别统计高校毕业生就业预测的训练和测试平均时间，结果如表3、表4所示。从表3可知，ACO-LSSVM的高校毕业生就业预测训练时间要明显少于LSSVM、PSO-LSSVM，同时从表4也可以发现，ACO-LSSVM的高校毕业生就业预测时间最短，主要是由于蚁群算法找到了更优的参数，最优参数加快了高校毕业生就业预测建模的速度，实际应用价值更高。

表3 高校毕业生就业预测的训练时间对比 单位:s

表4 高校毕业生就业预测的测试时间(s)对比

3 总结

高校毕业生就业一直是高校研究人员关注的焦点，其预测结果的科学性有利于高校开展就业工作，而高校毕业生就业是一个系统工程，牵涉到各方面因素很多，使得高校毕业生就业面临巨大挑战。为了有效改善当前高校毕业生就业预测效果，提出了基于大数据分析技术的高校毕业生就业预测方法，首先采用大数据分析技术拟合高校毕业生就业的变化规律，并引入群智能算法中的蚁群算法对预测模型参数进行优化，提高高校毕业生就业预测精度，测试结果表明，大数据分析技术较好的解决了当前高校毕业生就业预测中存在的一些问题，减少了高校毕业生就业预测误差，获得了比其它方法更优的预测结果，可以应用于实际的高校毕业生就业管理中。