基于源-荷-储互动的储能对风电消纳能力影响分析
程 瑜,陈 熙
(华北电力大学电气与电子工程学院,北京市 102206)
0 引言
随着具有随机性、波动性和分散性特点的新能源规模化接入电网,未来电网将呈现显著的“双侧随机性”,源网荷之间的构成形式、响应范围和交互模式较目前电网也将更趋复杂[1]。为实现“双碳”目标,提升新能源利用水平和电力系统运行效率,需要通过优化整合源侧、网侧与荷侧资源要素,以储能等先进技术和体制为支撑,实现源网荷储的深度协同[2]。所以因地制宜,适度配置储能成为推进源网荷储一体化的关键。
有关源网荷储协同优化调度的研究已有了一定的积累,但在规划层面考虑源网荷储深度协同的储能资源配置研究较少。研究较多面向微网或主动配电网,随着新能源场站大规模接入主干输电网,主干输电网调度中逐渐引入集中式电储能站[3]及需求响应资源[4]参与,构建广义源网荷储协调优化运营模式[5-6]。文献[7]针对储能辅助火电机组深度调峰建立优化调度模型,更多研究将储能作为灵活性资源纳入日前调度优化[8-11],文献[9]以最小化系统运行成本为目标,优化各类灵活性资源日前调度计划,并滚动修正日内出力;文献[10-11]考虑储能参与调频、调峰与备用辅助服务市场的应用前景,在日前阶段建立了储能多应用场景的协同优化模型。
参与调度运行的集中式储能资源配置决策已适度耦合系统运行约束,文献[12]在含储能设备的广义灵活电源规划模型加入了运行模拟校验;文献[13-15]建立了含网架结构约束[13]和低谷调峰及下备用约束[14-15]的储能配置统一优化模型,模型基于典型风出力场景,对风出力不确定性影响考虑不足;文献[16-18]基于设定的风出力不确定集合决策储能优化配置,但配置精度受限于模型中风电出力概率分布函数[16-17]或出力均值与上下限[18]对风出力不确定性映射的精准度。故现有含储能的调度模型及储能规划模型较常采用低谷调峰瓶颈约束、低谷下备用约束、弃风率指标等相对单一、静态的形式表征储能配置与风电消纳能力间的关联关系。
当前国内外学者已开展的鲁棒经济调度研究[19-22]为多维、动态展现储能配置对系统风电消纳能力影响,提供了一种可行的理论支撑。文献[20]提出调度中风电最大运行范围的评估方法;文献[21]建立风电可调度域分析模型,表征在给定运行点和备用水平下系统能够处理的风电不确定性范围;文献[22]考虑电网运行约束和再调度调节费用对实时调度灵活性的影响,提出实时调度能力及其边界计算算法。上述研究中主要计及常规机组增减出力的灵活性,对电储能、柔性负荷这类新兴灵活性资源缺乏考虑。灵活性资源的合理规划以及其对系统风电消纳能力影响的定量评价已成为高比例可再生能源电力系统建设的关键问题[23-24],储能配置对风电消纳能力影响的量化分析尚存在不足。
综上,本文基于含源-荷-储互动鲁棒经济调度,建立储能配置与风电消纳能力的关联分析模型,通过逐次生成割平面不断排除不可行点的算法,生成储能充放电调节、柔性负荷增减负荷调节与消纳风电波动范围三维变量的所有可行状态点集合构成的三维域区间,以直观刻画不同储能配置方案对系统风电消纳能力的影响,更好地实现源网荷储多资源协同增效,提升储能配置决策精益化水平。
1 储能影响风电消纳能力的问题描述
1.1 储能配置与风电消纳能力关联分析模型的构建思路
本文面向参与电网调度的集中式电化学储能资源的合理规划需求,建立储能配置与风电消纳能力的关联分析模型。模型基于源-荷-储三侧灵活性资源互动参与系统调度的背景,协同考虑源侧火电机组、荷侧可调节柔性负荷的调节能力,按调度时序分两阶段融合储能参与日前和实时2 个时间尺度的调度计划,侧重计及储能参与系统调峰、爬坡和提供旋转备用的贡献,量化分析系统对风电出力水平及其波动范围的接纳能力,以表征储能对风电消纳能力的影响。
第1 阶段,基于日前经济调度模型,量化储能在系统低谷、顶峰调峰和爬坡中的贡献;第2 阶段,在日前调度策略下,选取低谷或高峰时段,基于实时调度模型的约束条件,逐次生成割平面排除不可行点,获得满足约束的可行状态点集合的边界割平面。为了在三维空间直观刻画可行状态点集合,取可行状态点的风电波动量Δw、储能调节功率Δe、柔性负荷调节功率Δpcl这3 个变量,构成三维域区间。定义为储、荷调节与消纳风电波动范围三维域区间,表征储能、柔性负荷2 个控制因素分别提供一定调节能力时,系统消纳的风电波动范围。
三维域区间示意图如图1 所示。

图1 三维域区间定义及计算示意图Fig.1 Schematic diagram of definition and calculation of three-dimensional domain interval
图1 左侧为三维变量初始可调度区间,受灵活性设备个体运行特性约束、各条线路潮流约束等实时调度模型约束影响,逐次修正储能与柔性负荷可提供的调节能力,与常规机组调节能力共同影响系统消纳的风电波动区间,构成图1 右侧的三维域区间。
1.2 计及源-荷-储互动的协调优化调度模型
第1 阶段,计及储能与柔性负荷的参与,考虑弃风成本的影响,建立经济调度确定性优化模型。
1.2.1 目标函数

式中:T为调度周期的总时间;NG、Nw、Nes、Ncl分别为系统中的常规机组、风电机组的数量、储能与负荷的数量;c2、c1、c0为常规机组成本系数;cw、ces、ccl分别为单位弃风成本、储能的效率损失成本与柔性负荷调 节 成 本 系 数;和分 别 为 储 能 设 备k在t时 刻的 放 电 与 充 电 功 率;pi,t为 常 规 机 组i在t时 刻 的 发 电功 率;Wj,t和wj,t分 别 为 风 电 机 组j在t时 刻 的 预 测 出力与实际上网出力为柔性负荷q在t时刻的响应功率,设柔性负荷为正时代表减负荷量,为负时表示增负荷。
1.2.2 约束条件
1)功率平衡约束
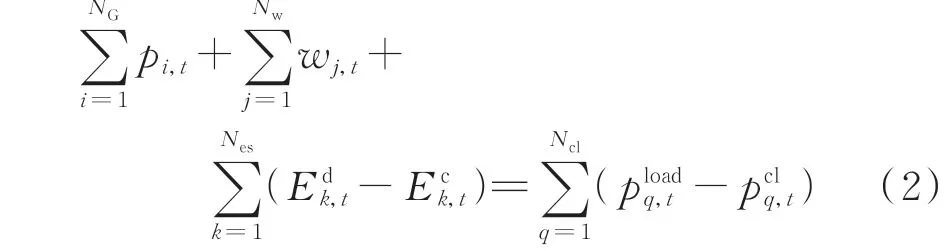

式中:πil、πjl、πkl、πql分别为常规机组i、风电机组j、储能设备k与柔性负荷q对线路l的潮流分布因子;Fl为线路l允许的最大传输功率。
3)机组出力约束

4)柔性负荷运行约束
式(7)为响应功率上限约束;本文选取可转移负荷做柔性负荷,式(8)表示可转移类型柔性负荷的总用电需求不变,净负荷响应增减总电量为0。
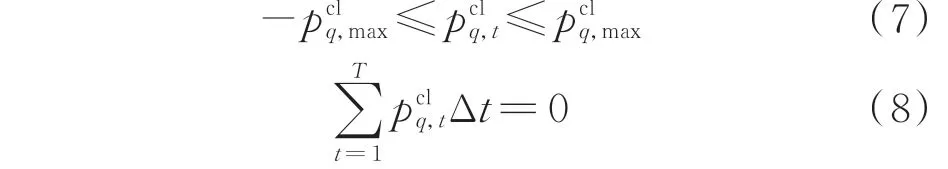
5)储能系统的运行约束
储能系统的运行约束包括充电或放电状态不同时的约束(式(9))、荷电状态约束(式(10)至式(13))和储能设备在调度周期内始末蓄电量不变的约束(式(14))。

式 中:ck,t和dk,t分 别 为 储 能 设 备k在t时 刻 的 充、放 电状态,取1 时分别表示处于充电或放电状态,取0 时分 别 表 示 未 处 于 充 电 或 放 电 状 态;Ek,t和Ek,ini分 别为储能设备k在t时刻的蓄电量与一天中的初始蓄电量;γc和γd分别为储能系统的充、放电效率;Pk和分别为储能设备k的额定功率与额定容量。
基于给定的风电出力预测曲线,求解上述经济调度确定性优化问题(式(1)至式(14)),得到经济调度 策 略 解X={p,w,Ec,Ed,c,d,pcl},对 应 为 火 电机组出力、风电实际上网出力、储能充放电功率及状态、柔性负荷响应功率的向量表示。
第2 阶段,由于考虑风电出力预测误差,在上述确定性经济调度策略的基础上,以调度机组、储能设备、柔性负荷灵活性资源实现功率平衡的再调度成本最小为优化目标,建立优化模型。
1)目标函数
灵活性资源的调度成本主要包括常规机组调节成本、储能设备充放电成本与柔性负荷调节成本。

2)约束条件
约束条件包括功率平衡约束(式(16))、线路潮流约束(式(17))、机组出力约束(式(18)和式(19))、储能运行约束(式(20)至式(22))和柔性负荷调节区间约束(式(23)),再调度策略基于确定时刻t下的经济调度策略得到,故式中省略时刻t。

式中:Δwj为t时刻风电机组j的出力波动量。
满足约束式(16)至式(23)的可行的调度策略表示为{p+,p-,Δw,Δe,Δpcl},对应为火电机组向上和向下调节功率、系统消纳的风电波动量、储能调节功率、柔性负荷调节功率的向量表示。取其中风电波动量Δw、储能调节功率Δe、柔性负荷调节功率Δpcl这3 个向量值,构成三维可行状态点Δr={Δw,Δe,Δpcl},表征系统可实现的调节状态点,即储能、柔性负荷2 个控制因素分别具备Δe、Δpcl调节能力时,系统消纳风电波动量Δw。由所有可行的三维可行状态点构成的集合RAct反映了在常规机组可上下调整的能力范围内,满足系统运行约束的储能、柔性负荷调控量与系统消纳的风电出力变化量的系统运行点的最大集合,如式(24)所示。

式中:RAct为储、荷调节与消纳风电波动范围三维域区间集合;Y={p+,p-}为常规机组可上下调节的出力范围;A、B、D、b为系数矩阵。
为量化表征系统的风电消纳能力,根据集合RAct中消纳风电波动范围维度上的边界值,定义为系统消纳的风电波动区间Wmargin,反映系统风电消纳能力大小,如式(25)所示。
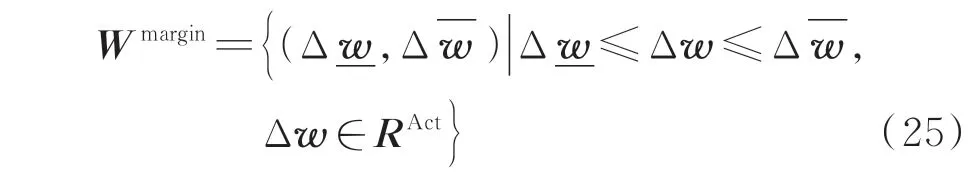
2 储能配置与风电消纳能力关联分析模型求解算法
根据式(24)对于储、荷调节与消纳风电波动范围三维域区间集合的定义描述,风电消纳能力的计算本质上是一种最大-最小问题的求解,即寻找电网在系统灵活性最糟糕的情况下,调用向上与向下灵活性调节资源松弛变量的成本最小时的调度策略边界,见式(26)。

式中:s+和s-分别对应为Y中p+、p-的松弛变量,问题(26)的约束为加入了松弛变量的常规机组出力相关约束(对应系数矩阵为A1、B1、D1、b1)以及无松弛变量的约束、柔性负荷运行约束与储能运行约束(对应系数矩阵为A2、B2、D2、b2);I为单位矩阵,矩阵维度与A1相同。
若问题(26)有解,当最优值大于0 时,表示Y需要松弛变量才能满足系统运行约束,系统灵活性不足;当问题最优值为0 时,电网仍有灵活性,集合RAct非空。
为得到问题(26)的解,通过拉格朗日函数对上述问题求对偶,将问题转化为对偶问题(27)。
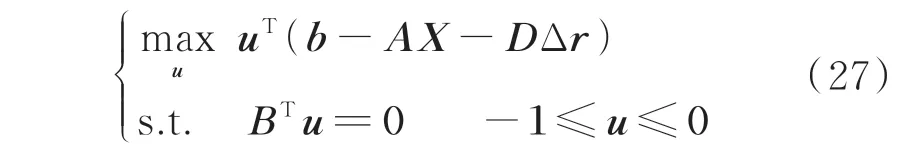
决策变量为对偶变量u,问题转化为通过对原问题中各约束进行稀缺资源定价,得到各种灵活性条件下的最优解。为得到非空集合RAct,根据强对偶性,对偶问题(27)最优解为0,有:
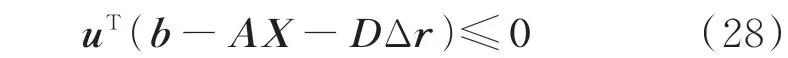
此时根据式(28),三维域区集合RAct可被重新描述为:
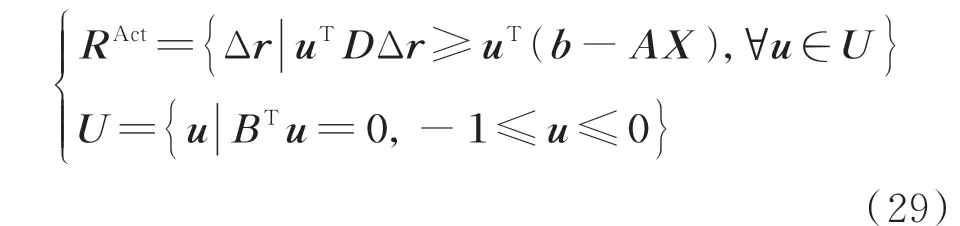
问题重新回到三维域区间集合RAct的计算,此时储能影响的三维域区间集合RAct表示为多面体,写作线性不等式,有限数量的顶点由集合U表示[21]。但由于顶点数量过多,列举所有顶点u耗时过久。文献[22]提出了一种自适应约束生成算法,通过寻找相应的关键顶点,在每次迭代中生成超平面约束,减少计算时间。结合约束生成算法,计算三维域区间集合的具体过程如下。
对于Δr*∉RAct,存在相应的u*使下式成立:
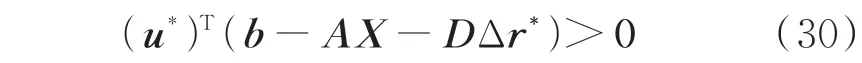
设 一 个 足 够 大 的 基 础 集 合RAct={Δr|HΔr≥h},其中H与h为系数矩阵,将不属于集合RAct的向量Δr*从中分离,直至集合内任一向量均不使式(30)成立,此时集合RAct即为所求。
为分离不属于集合RAct的向量Δr*,生成加入集合RAct的割平面约束,需要找到满足式(30)的Δr*和对应的u*,问题(26)转化为求下述双层规划问题的最大值。
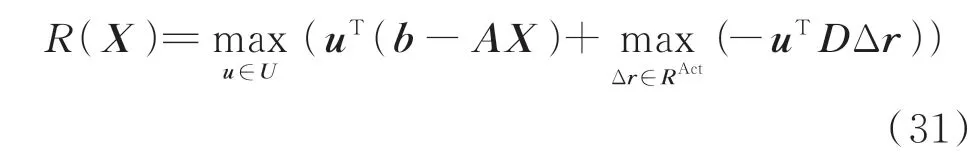
当u=0 时,R(X)=0,由式(27)可知,R(X)≥0 总成立;若R(X)=0,表示对RAct内任意X,Y非空;若R(X)>0,最优解Δr*不属于集合RAct。
对问题(31)中二次项的线性约束求对偶后,其中非线性约束为互补松弛约束。通过大M法将互补松弛约束转化为线性约束,问题(31)可转化为如下混合整数线性规划(mixed-integer linear programming problem,MILP)问题。
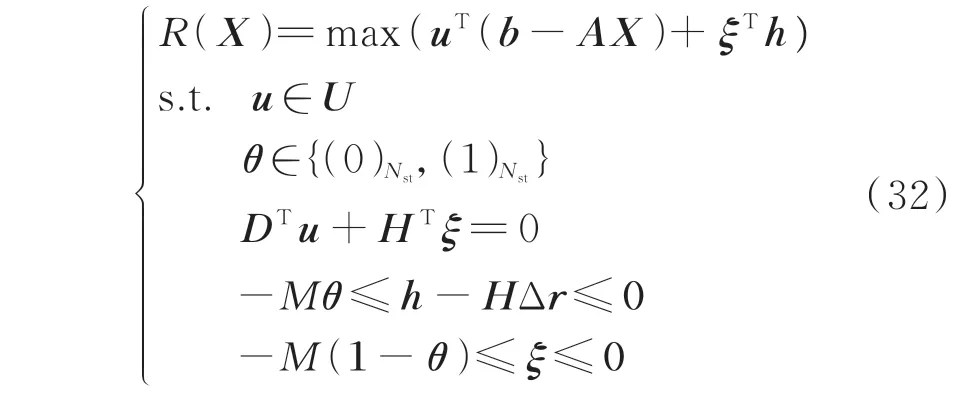
式中:ξ为线性规划问题的对偶变量;Nst为RAct中矩阵的维数;M为足够大的正数。
求解储、荷调节与消纳风电波动范围三维域区间集合式(24)转化为优化问题(32),详细推导过程见附录A。当问题(32)最优值R(X)=0 时,RAct即为所求的三维域区间集合,算法流程如附录B 图B1 所示。
3 算例分析
本文选取改进的IEEE 30 节点系统进行算例分析,网络拓扑结构见附录B 图B2,线路参数设置详见附录B 表B1。该系统含有5 台传统发电机组,分别位于节点1、2、3、5、8,机组参数设置详见附录B表B2;风电、负荷预测出力数据详见附录B 图B3 和图B4;基础场景中柔性负荷可调用的调节功率上限为50 MW;储能容量为100 MW·h,额定功率为50 MW,充、放电效率为90%。
选取典型规划场景中风电大发且负荷低谷时段,风电出力小且负荷尖峰时段的调峰瓶颈时段作为储、荷调节与消纳风电波动范围三维域区间分析的典型时段,并考虑依据后续时段的滚动运行模拟校验,修正决策适宜的储能配置容量。仿真算例运行环境为Intel i5 CPU 和16 GB 内存,本文所建MILP 模型通过调用CPLEX 求解器进行求解。
3.1 储能布点对风电消纳能力的影响分析
根据本文模型,储、荷调节与消纳风电预波动范围三维域区间的边界取决于系统运行的各项约束。考虑线路输送能力对储能发挥调节作用的约束,储能位置及其与可再生电源、柔性负荷的空间布点关系直接影响与网架约束的耦合强度。
采用本文模型,分别计算储能装置与柔性负荷不同空间布点4 种场景下的风电消纳能力。各场景储能和柔性负荷布点设置如表1 所示:场景a 中储能配置在节点6,柔性负荷布点在节点24 的PL1,设场景a 为基础场景;场景b 中储能布点调整至风电机组接入的节点7;场景c 中储能布点调整至远离风电机组且靠近柔性负荷PL1的节点23;场景d 中进一步拉大储能与柔性负荷间的电气距离,把柔性负荷调整到节点14 的PL2。

表1 不同场景中的储能与柔性负荷布点情况Table 1 Energy storage and flexible load distribution in different scenarios
基于上述4 种布点场景,分别考虑200、300、400 MW 这3 种水平的风电机组容量,对应情况1、2、3,分别按风电机组容量的20%配置储能容量,计算系统消纳的风电波动区间如表2 所示。
由表2 可知,配置储能可提升风电消纳能力,当依据风电场容量的固定比例配置储能时,例如本例都取20%,伴随系统风电容量占比的提高,配置储能对提升系统调节能力的作用将呈现相对放缓的趋势,即伴随风电装机占比的提升,需求配套储能容量占风电机组容量的比例可适当减少。
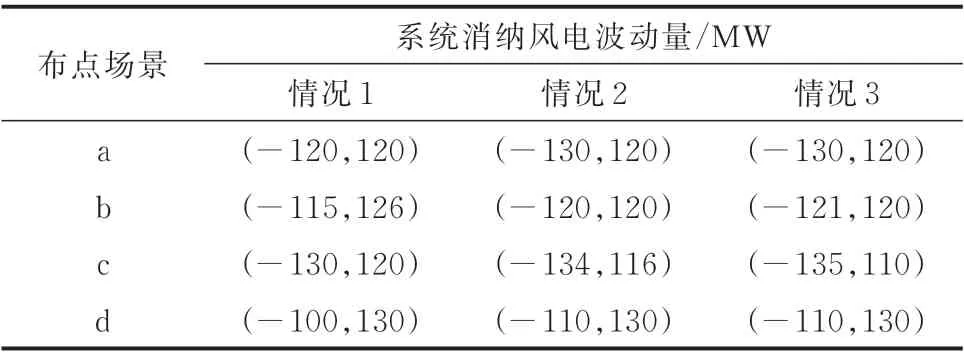
表2 不同风电机组容量的系统消纳风电波动量Table 2 Wind power accommodation fluctuations of systems with different wind turbine capacities
图2(a)展示了场景a 下储能配置与风电消纳能力关联分析三维域区间立体示意图,图中3 个坐标轴分别对应储能调节功率Δe、柔性负荷调节功率Δpcl以及消纳的风电波动范围Δw。其中,图2 分别针对风电波动量达到30 MW 与60 MW 情况做三维域区间的切割截面,各切割截面示意图如图2(b)与(d)所示。由式(29)可知,三维域区间集合由不等式方程组表示,体现储能与柔性负荷在参与日前经济调度后剩余调节能力与消纳风电波动范围,切割后二维截面图展示了限制储能、柔性负荷调节与消纳风电波动区间波动的约束边界。因此,图2(b)二维截面图的上边界U1 与下边界D5 为柔性负荷调节功率上下限约束;左边界L3 与右边界R4 为储能调节功率约束;上边界U2 为线路22-24 容量约束;当风电波动在30 MW 时,柔性负荷调控量受U1、U2 与D5 共同约束,储能放电调节量高于4.1 MW 时,柔性负荷开始受限于约束U2;当风电波动量进一步增至60 MW 时(对应图2(d)),线路22-24阻塞情况加重,此时柔性负荷调节能力上界仅受限于U2 约束,即主要受到线路22-24 容量约束。

图2 场景a 下风电波动量为30 MW 与60 MW 时的三维域区间集合示意图Fig.2 Schematic diagrams of three-dimensional domain interval set in scenario a when wind power fluctuation is 30 MW and 60 MW
图3 中绘制了表1 中各场景的储、荷调节与消纳风电波动范围三维域区间以及消纳风电波动区间在风电出力波动与储能充放电调节域平面的投影。由图3 可以看出,在系统储能和柔性负荷灵活性资源总量相同的情况下,不同储能布点场景下系统可消纳的风电波动范围基本相似,但各个场景下储、荷调节与消纳风电波动范围三维域区间的空间形状不同。
1)图3 中,图3(b)与(a)相比,三维域区间的运行范围区别不大,但图3(a)中的三维域区间由更多的平面包围形成,表明当储能分布于节点6 时,系统为平衡风电的波动量所进行的源-荷-储互动受到更多的运行约束限制;图3(b)中储能直接布点在风电场接入节点,风电机组与储能之间的互动无线路容量约束的限制,储能与风电机组之间互动将更加频繁,此时储能可在风电大发负荷低谷时段储存电能,在风电低谷负荷高峰时段放电,从而减少线路容量约束对风电出力的影响。
2)图3(c)在柔性负荷调控维度方向的三维域区间较图3(a)有大幅提升,即当风电出现波动时,在常规机组可调节出力范围内,储能与柔性负荷互动可提供更多的调节能力,这说明相较于分布在节点6 与节点7 的储能装置,选址于节点23 的储能与柔性负荷之间互动受网络约束的影响更小。
3)图3(d)在柔性负荷调控维度方向的三维域区间范围较图3(a)明显变小,此时系统灵活性主要依靠储能与常规机组互动调节能力,当柔性负荷位于节点14 的PL2时,柔性负荷与储能之间互动受系统网络约束的影响减弱,且此时系统消纳风电波动正偏差的能力受到机组向下调节能力约束的影响而达到限值。
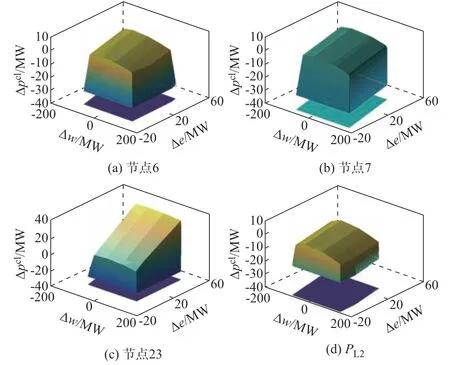
图3 不同储能并网节点的储、荷调节与消纳风电波动范围三维域区间集合示意图Fig.3 Schematic diagrams of three-dimensional domain interval set of storage,load regulation and acceptable wind power fluctuation range of different energy storage grid-connected nodes
3.2 储能容量对风电消纳能力的影响分析
系统配置不同容量的储能时,对于三维域区间的影响也会有所不同。图4 展示了同一布点处,3 种不同储能容量E(100、150、200 MW·h)的储能配置方案下调峰瓶颈时刻的风电消纳能力。表3 列出了不同容量的储能配置方案在低谷和峰荷时段,系统所能接受的风电波动区间范围。
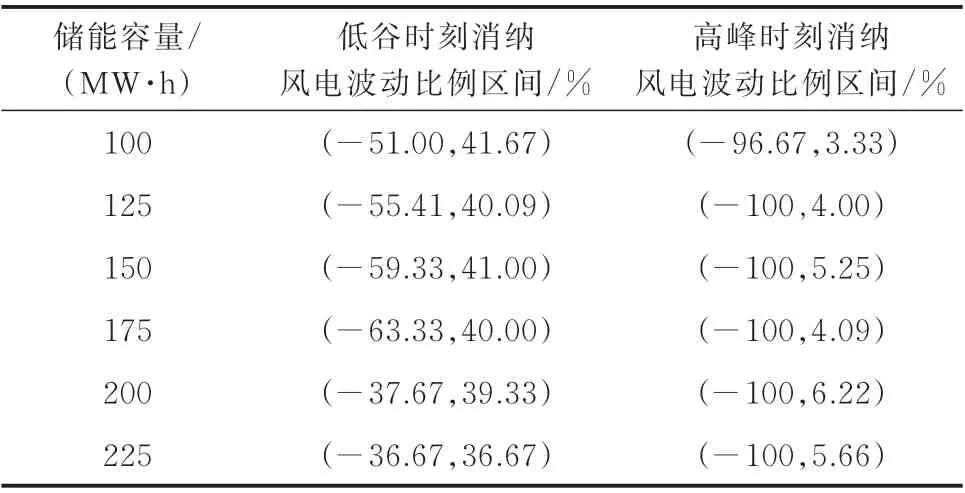
表3 不同储能容量配置下系统消纳风电波动比例区间Table 3 Wind power accommodation fluctuation ratio interval of system with different energy storage capacity configurations

图4 不同储能容量配置下储、荷调节与消纳风电波动范围三维域区间集合示意图Fig.4 Schematic diagrams of three-dimensional domain interval set of storage,load regulation and wind power accommodation fluctuation range with different energy storage capacity configurations
由图4 可知,受到风电场、储能和负荷之间的线路容量约束以及机组运行约束的影响,源、储、荷三维域区间并未随配置的储能容量增长一直扩大。
由表3 可知,算例中系统可消纳的风电波动范围随配置储能容量的增长而增大,但当储能配置容量高于175 MW·h 后,储能配置对系统应对风电出力预测偏差的调节能力的提升已达到相对饱和的状态,此时再增加储能配置容量,无法明显增大系统消纳的风电波动区间。
3.3 储荷容量配比对风电消纳能力的影响分析
随着柔性负荷接入电网的规模不断扩大,储能与柔性负荷间的容量配比关系也会影响互动域区间。本文对比分析3 种储荷配比场景:1)场景1 中储能容量E为30 MW·h,柔性负荷容量PL为70 MW;2)场景2 中储能容量E为50 MW·h,柔性负荷容量PL为50 MW;3)场景3 中储能容量E为70 MW·h,柔性负荷容量PL为30 MW。3 种场景的三维域区间集合示意图如图5 所示。

图5 不同储荷配比方案下储、荷调节与消纳风电波动范围三维域区间集合示意图Fig.5 Schematic diagrams of three-dimensional domain interval set of storage,load regulation and acceptable wind power fluctuation range with different ratios of load and storage configuration
图5(a)相比于图5(c),可调度的柔性负荷范围更大,但储能受容量约束限制,其调节能力最弱。图5(a)与(c)中系统消纳的风电波动区间范围分别为(-125 MW,117 MW)与(-126 MW,130 MW)。场景2 中储能与负荷比例相等,由图5(b)可知,系统消纳的风电波动区间为(-141 MW,124 MW),此时储能和负荷分别位于节点6 与节点24,场景2 可消纳的风电波动范围最大。因此,储能的规划需要结合荷侧柔性负荷资源规模化聚合发展布局、响应成本下降和多元化发展等因素进行合理的储能容量配置和布点规划。
3.4 调峰瓶颈后续时段消纳风电波动区间检验
调用储能资源应对调峰瓶颈时段的风电波动量,将导致储能后续时刻的荷电状态发生变化,从而影响系统在后续时刻储能可用的调节能力。故有必要进行调峰瓶颈后续时段消纳的风电波动区间检验,并根据检验结果调整修正储能配置容量。
以3.1 节中场景a 为例,算例低谷和高峰调峰瓶颈分别开始于05:00 与15:00 时,并后续各持续1 h。采用本文模型,对调峰瓶颈后续时段消纳的风电波动比例的区间进行检验,如表4 所示。

表4 调峰瓶颈后续时刻消纳风电波动比例区间检验Table 4 Test of acceptable wind power fluctuation ratio interval at subsequent moments of peak shaving bottleneck
根据表4 可知,对于低谷调峰时刻05:00,当风电波动正偏差超过3.33%(或10 MW)时,系统在后续时刻06:00 时就会缺乏调节能力以应对风电波动,可见本例中100 MW·h 的储能配置规模难以满足05:00—06:00 时低谷调峰瓶颈时段的调节能力需求;对于高峰时刻15:00 时,即使风电波动偏小20%,后续时刻16:00 系统仍消纳不超过27.00%的风电波动负偏差。受线路6-7 容量约束影响,场景a配置储能无法应对风电波动偏大20%的情况,若将储能布置在风电场节点,如场景b,风电波动偏大20%仅需配置150 MW·h 储能。因此,在储能配置决策中,需结合规划地区的低谷调峰瓶颈时段的风电功率波动范围以及调峰瓶颈持续时长,利用本文模型进行调峰瓶颈后续时段消纳的风电波动区间检测,以决策适宜的储能配置规模。
4 结语
为定量分析储能对源-荷-储互动场景下系统风电消纳能力的影响,本文采用鲁棒经济调度模型的约束生成方法,建立了储、荷调节与消纳风电波动范围三维域区间计算模型,量化表征储能、柔性负荷灵活调节能力适应风电出力波动的三维域区间边界。
1)储能与柔性负荷资源、可再生电源的空间布点是影响源网荷储互动场景下系统风电消纳能力的重要因素。受网络约束的影响较小的储能布点,源网荷储协同增效能力强。
2)由于网架约束和常规机组运行约束,增加储能配置容量对系统应对风电出力波动的调节能力的提升将会出现相对饱和的状态。结合电网网架结构及其发展规划合理配置储能容量,有利于提升储能配置的经济性,减少冗余投资。
3)不同的储能与柔性负荷的容量配比影响系统风电消纳能力提升。算例中,储能与柔性负荷采用等比例配置,系统消纳风电波动区间最大。
综上,通过三维域区间可有效刻画储能配置策略提升系统调节能力的影响,实现系统消纳风电波动范围波动区间与储能配置策略间的交互分析。市场机制下,有待进一步结合储能协同参与电能量交易和多时间尺度、不同方向调频和备用辅助服务交易的时序耦合特征,计及储能设备复杂多重复用场景,研究适应系统调节能力提升需求的储能配置策略分析模型。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

