三板溪面板堆石坝流变特性及面板脱空效应

蒋中明，杨江寅，孙 盼，廖峻慧

(1.长沙理工大学 水利工程学院，长沙 410114； 2.长沙理工大学 水沙科学与水灾害防治湖南省重点实验室， 长沙 410114； 3.云南省港航投资建设有限责任公司，昆明 650000)

1 研究背景

面板堆石坝具有安全、经济、施工速度快等优点，因而被广泛应用[1]。面板脱空是威胁到面板堆石坝安全性的重大隐患之一，其主要危害包括：一方面，面板脱空可能导致面板出现结构性裂缝，破坏大坝的防渗体系，危及大坝的运行安全[2]；另一方面，坝体流变变形将加剧面板脱空效应，劣化大坝的运行条件[3]。

根据《三板溪大坝安全监测资料分析报告》(中国水利水电科学研究院，2016)[4]，该面板堆石坝自2005年建成以来，主坝表面变形仍在继续，截至2016年底，表面最大沉降变形近0.6 m，且还未收敛。同时，面板在380～400 m高程左右出现较大范围的脱空现象，其中脱空测点M2-05x的最大脱空量达到3.0 cm。伴随面板脱空现象的出现，面板混凝土还出现了挤压破坏的现象。该工程面板在经过多次维修后(《三板溪水电站大坝面板局部破损处理及效果评价报告》，2016)[5]，仍然没有完全解决由于脱空而导致的面板破坏问题。为此，深入认识坝体变形发展和面板脱空及破坏机理是研究面板修补措施的基础。

研究表明[6-11]，坝体变形具有复杂的非线性和弹塑性特点，且存在显著的流变效应。堆石坝填筑料应力变形分析常用的本构模型有非线性邓肯张E-μ、E-B模型、双屈服面弹塑性模型和沈珠江模型等[6]。邓肯张E-B模型能反映填筑料变形的非线性特性，因而在工程界应用广泛[7-8]。堆石料流变效应数学模型主要有理论模型和经验模型两类[9]。其中，常用的经验模型有时间对数函数、指数衰减曲线和双曲线函数[10]。冉蠡等[11]的研究表明，采用Burgers流变模型分析得到的流变变形与工程实际情况吻合度较高，可以较好地反映堆石料的流变特性。

面板脱空出现的原因是面板与坝体之间存在不协调变形，这种不协调变形随着坝体后期流变变形增加而加剧。面板与坝体间的不协调变形可采用接触力学理论进行分析，进而评价面板可能产生的脱空区域及脱空值[12-18]；在数值模拟技术方面，可采用隐单元[13]和接触单元[14]来模拟面板与垫层的脱空效应。尽管目前在面板堆石坝脱空效应的研究方面取得了较多研究成果，但这些成果在面板堆石坝三维空间流变效应的脱空机制分析方面仍显不足。因此，本文针对三板溪面板堆石坝长期变形和脱空问题，在研究面板脱空定量分析方法的基础上，采用堆石体三维流变变形分析方法，结合工程实测资料，探讨其面板脱空的三维分布特征及形成机制。

2 脱空分析算法及程序二次开发

2.1 脱空分析算法

面板脱空分析的数值方法主要有3类：面板和垫层相对变形分析法[15]、基于直接约束算法的接触力学分析法[16]和隐单元模拟脱空分析法[17]。本文基于面板-垫层无厚度接触面模型，提出利用接触面单元节点的变位信息来确定面板脱空位置及脱空值。

2.1.1 脱空位置确定

面板与垫层的相对位移形式有相互嵌入、错动变位及法向脱空3类。为避免因相互嵌入引起的脱空误断，引入叉乘向量判断垫层相对于面板的位移方位,如图1所示。

图1 面板脱空关系示意图Fig.1 Schematic diagram of disengaged concrete slab

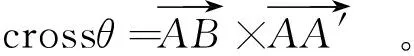
(1)

2.1.2 脱空值计算

接触面变形后AA′与AB之间夹角的余弦值计算方法为

(2)

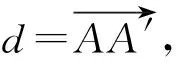
(3)

式中d为垫层网格节点A′的位移;dp为变位后节点A′相对于混凝土面板的垂直距离，即脱空量。

通过脱空值的计算可进一步排除因错动变位导致的脱空误判：当crossθ>0，dp=0且d=0时，面板与垫层保持紧密接触，且面板与垫层之间无错动；当crossθ>0，dp=0且d≠0时，面板与垫层保持紧密接触，且发生了错动变位；当crossθ<0，且d≠0时，面板与垫层处于脱空状态。

确定面板脱空位置和脱空量的前提是获得接触面单元两侧节点的位移量。本研究中混凝土面板采用摩尔-库伦弹塑性模型，各种堆石料、垫层等采用邓肯-张非线性弹性模型；在计算过程中，采用Burgers流变模型来分析堆石料及垫层等材料的流变特性对坝体变形的影响。

2.2 程序二次开发

基于FLAC3D软件平台，采用上述模型和算法开发了可计算面板堆石坝三维瞬时变形和流变变形的FISH程序，以及面板脱空计算分析的FISH程序，其计算流程如图2所示。其中n为填筑期，本次计算n值取5，Mmax为当前填筑期的最大填筑层数，K、G分别表示体积模量和剪切模量，Imax为最大接触面单元节点编号。FLAC3D软件没有提供邓肯-张模型，故同时二次开发了邓肯-张模型计算子程序。

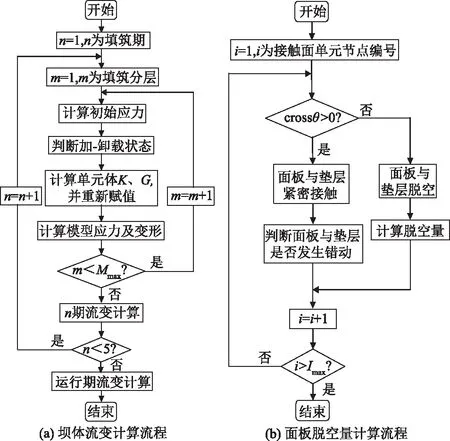
图2 坝体流变和面板脱空量计算流程Fig.2 Flow chart of computing the rheological deformation and disengaged distance of face slab

3 程序验证

为验证二次开发程序的正确性，选择文献[19]中的三板溪面板堆石坝为例进行验证。算例计算网格模型及分区示意如图3所示，模型材料从左至右依次为面板、垫层区、过渡区、上游堆石区和下游堆石区。计算考虑分期填筑的影响，面板分3期，坝体主堆石料分5期填筑。表1为计算参数取值，参数的选取依托于文献[19]及三板溪面板堆石坝监测报告。在邓肯-张模型中，参数γ为重度；K表示初始变形模量Ei的基数；Kur为lg(Eur/pa)和lg(σ3/pa)关系直线的截距，是反映土体卸载的参数；N反映Ei随σ3增长的速率；Rf为破坏比，反映(σ1-σ3)f与(σ1-σ3)u之间的关系；Kb表示K的基数；m反映K随σ3增长的速率；φ与Δφ共同表示当围压σ3不断变化时的内摩擦角。

表1 算例计算参数Table 1 Computation parameters of verification example

图3 验证算例计算网格Fig.3 Computational meshes of verification example

图4为竣工时的坝体沉降变形等值线图。由图4可知，采用笔者二次开发的程序计算得到的坝体最大沉降变形为85 cm，发生在坝体中部。宋文晶等[19]采用清华非线性K-G模型计算得到的竣工期最大沉降约为86 cm，两者结果基本一致，表明本文二次开发计算程序是正确的。

图4 坝体竣工沉降变形Fig.4 Settlement contours of dam at the completion of construction

为验证面板脱空计算模块的正确性，采用FLAC3D的Interface单元对图5所示的算例模型进行了计算。图6为FLAC3D输出的接触面接触状态标志图，其中实心圆圈表示该节点位置界面处于接触状态，空心圆圈表示该节点位置界面发生了分离。根据本文提出的接触面算法，编号为33—40,59—62,80—83的节点发生了脱空现象，脱空位置与FLAC3D软件给出的位置相同。表2给出了面板接触面脱空位置的脱空量值。由此可见，本文提出的算法不但可以判断出脱空位置，还能计算出具体的脱空量数值。

图5 脱空算法验证模型Fig.5 Model of validating the computation method for disengaged distance of face slab

图6 接触面状态分布Fig.6 Distribution of contact surface

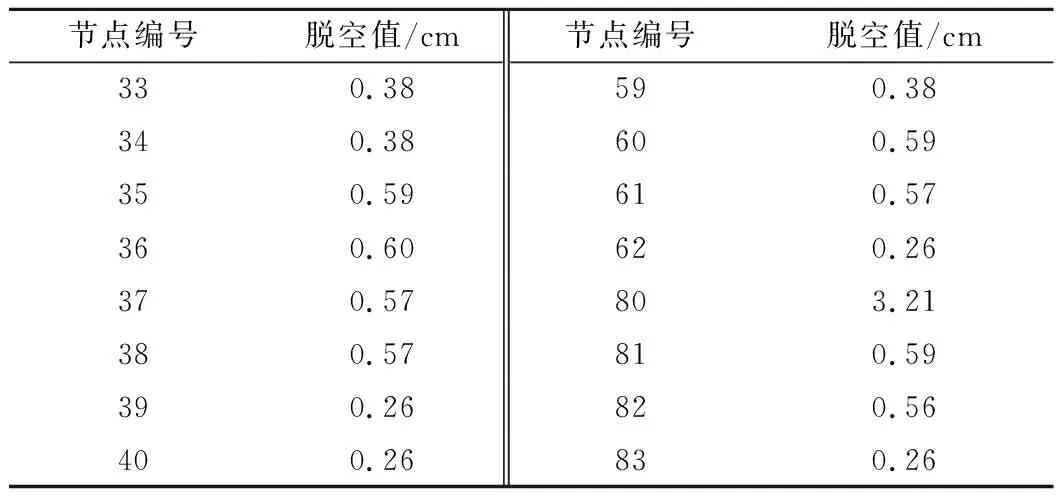
表2 接触面脱空值统计结果Table 2 Statistics of disengaged distance of contact surface

表3 邓肯张E-B模型参数Table 3 Parameters of Duncan-Chang E-B model

4 三板溪面板堆石坝变形及面板脱空分布特性研究

4.1 工程概况

三板溪工程位于贵州省境内的沅江流域，主坝为混凝土面板堆石坝，坝顶高程482.5 m，坝高185.5 m，是国内第二、世界第三的大(1)型高坝工程。坝体从上游至下游分为面板、垫层、过渡区、主堆石区和次堆石区。据三板溪大坝监测资料分析报告，面板堆石坝在运行过程中发生了显著的流变及脱空现象，为深入分析二者之间关系，采用三维流变和面板脱空分析方法对此进行研究。

4.2 计算模型

根据坝体工程实际的分区特点及施工填筑方案，建立大坝三维计算网格模型。如图7所示，取顺水流方向为x正方向，竖直向上为z轴正方向，由河道位置指向左岸为y轴正方向。坝体、地基和周围山体采用8节点六面体单元模拟，坝体与周围山体间的过渡带采用四面体单元划分。计算模型的网格节点数为36 996个，单元总数为55 202个，模型的铅直边界及底面均为位移约束边界。

图7 三维计算网格Fig.7 Three-dimensional computation meshes

本文在验证算例中虽然模拟了分层填筑对坝体最终变形的影响，但未考虑分层填筑期坝体产生的流变效应，与工程实际情况不符。为此，采用位移反分析法确定的计算参数见表3、表4。由于坝体竣工后受较大水荷载作用，坝体材料产生了压密效应而导致其流变力学性能与施工期存在较大差异。因此，对不同流变计算阶段的模型参数也进行区分，如表4所示。

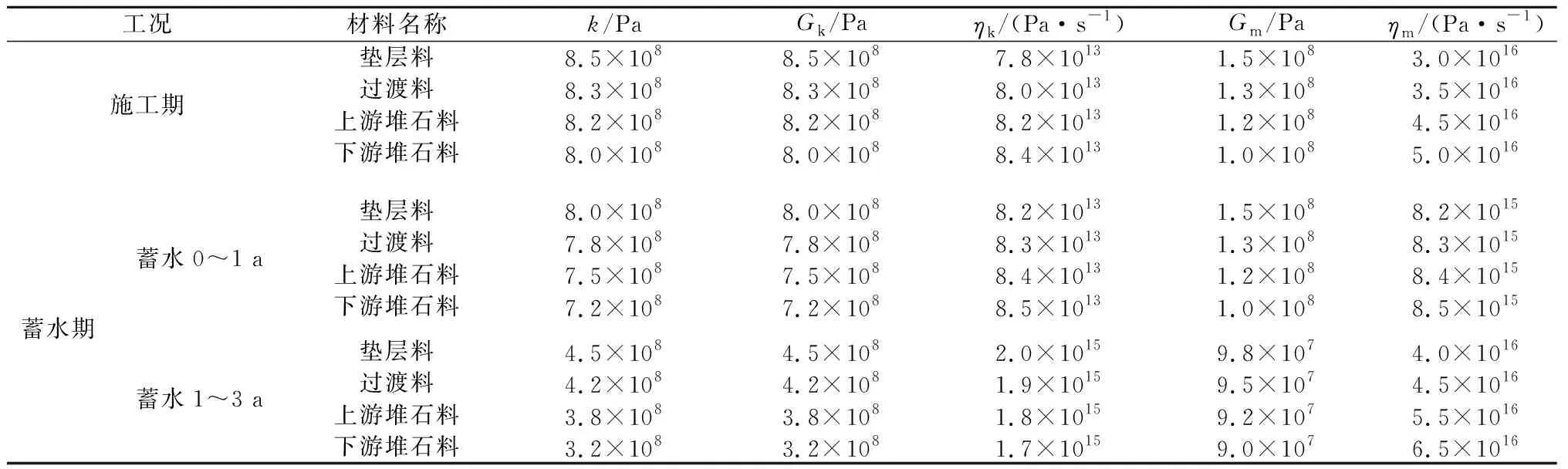
表4 流变模型参数Table 4 Rheological model parameters

三板溪工程在建设过程中，分别在主坝表面的坝顶部位和坝右0+71.8断面上布置了变形过程监测点，如图8所示。

图8 位移监测点布置Fig.8 Layout of displacement monitoring points

坝体采用5期填筑施工方案，填筑期为2003年12月1日至2005年9月15日，历时21.5个月；面板分3期施工。图9为坝体施工分层填筑顺序图，其中①—⑤表示填筑分期序号，①—⑤期施工又采

图9 坝体施工分期填筑Fig.9 Diagram of staged-filling of dam construction

取了分层填筑的方法，按顺序各填筑期的分层数量分别为5、4、3、3、2。

根据分期填筑的实际时间，拟定数值模型计算过程：首先采用邓肯张模型计算每一个填筑期产生的瞬时加载变形，随后采用流变模型对该填筑期形成的坝体结构进行流变变形计算，当前填筑期流变变形计算完成后，再进行下一填筑期瞬时加载变形计算和流变变形计算。以此类推至坝体施工模拟完成。按施工分期顺序，5个流变变形计算时间分别为5、5、3、5和3.5个月；面板竣工后蓄水前的流变计算时间为3.5个月；水库蓄水后先用邓肯张模型计算坝体在蓄水压力作用下的变形，再用流变模型计算3 a时长的流变变形。

4.3 计算成果及分析

4.3.1 坝顶及坝体测点变形过程分析

图10为坝顶典型测点的沉降变形过程线。2006年1月1日坝体开始蓄水至死水位，在瞬时蓄水荷载作用下，坝顶测点SA5-3的瞬时沉降约为0.05 m。在坝体流变效应的作用下，其沉降随时间的推移继续增加，至2006年3月14日达到约0.15 m，随后沉降值呈现稳定变化的趋势。2007年1月1日开始，水库逐渐蓄水至设计水位高程。在新增的库水压力和坝体材料流变效应的作用下，坝顶测点SA5-3沉降值又逐渐增加。该测点沉降值在2007年12月5日左右达到约0.30 m，此后呈缓慢增加的趋势。坝顶其他测点(SA5-4、SA5-5和SA5-6)都表现出同样的变化规律，但其沉降变形的数值不同。

图10 坝顶测点沉降过程线Fig.10 Settlement processes of measuring points at dam crest

坝顶沉降变形随时间的变化过程表明三板溪面板堆石坝的流变效应显著。考虑三维空间流变效应的情况下，坝顶各部位测点的沉降变形计算值与实测值在变形趋势和变形量值方面都拟合良好，说明本文采用的计算模型和计算方法能够较好地模拟出坝体表面的坝顶沉降变形过程。

图11为坝右0+071.80断面内部的测点沉降变形计算值与实测数据的对比过程线。测点SVB1-3、SVB2-4、SVB3-5和SVB4-6分别位于⑤、④、②和①填筑期填筑分层面上。图11中测点沉降计算值出现阶跃性变化的原因是数值计算方法中，假定各分期填筑荷载作用是瞬时完成的，故其变形在计算过程中也瞬时完成的。工程实际填筑加载情况则是坝体分层碾压，荷载缓慢增加，故其实测沉降值也是逐步增加的，因而导致计算结果和实测结果的变化规律在此期间出现了较大的差异性。

图11 坝体内部测点沉降过程线Fig.11 Settlement processes of measuring points inside the dam

由图11可知，坝体内部测点SVB1-3、SVB2-4、SVB3-5和SVB4-6在竣工时实测沉降变形分别为0.80、1.03、1.18、0.77 m，蓄水运行3 a后沉降变形分别增加到1.08、1.32、1.30、0.88 m，沉降变形增加的幅度分别为35%、28.1%、10.1%和14.2%。由此可见，坝体内部不同位置的测点流变变形量表现出了显著差异性；其中坝体内中下部位的流变变形量相对较小，坝体中上部位置的流变变形相对较大。

4.3.2 坝体变形空间分布特征

图12及图13为蓄水至设计水位并运行3 a后的坝体河床断面和坝轴线剖面的位移等值线。由图12可知，蓄水运行3 a后，顺河床断面坝体向上游方向的最大水平位移发生在上游坝体的中下部位，最大值有0.40 m；向下游方向的最大水平位移发生在下游坝体中下部位，最大值为0.60 m；坝体中间部位最大沉降达到1.30 m。图13表明坝轴线断面在蓄水运行3 a后，靠近岸坡处坝体的水平位移基本不变，说明两岸山体对坝体的约束作用良好，坝轴线断面最大沉降发生在断面中间部位，达到1.20 m。

图12 河床断面(0+0)位移等值线Fig.12 Displacement contours of cross section 0+0 m

图13 坝轴线断面位移等值线Fig.13 Displacement contours of longitudinal section

需要说明的一点是，本文计算得到的等值线呈锯齿状分布，这种分部规律与现有大多数文献提供的等值分布图规律不同，其原因是计算过程中考虑了坝体分期和分层填筑效应的结果，如果不考虑分层和分期填筑的影响，计算位移的等值线是光滑连续的。施工期和运行期坝轴线断面与河床断面的变形总体上均符合坝体已知变形规律。

4.3.3 堆石料流变效应对坝体变形的影响分析

表5为考虑与不考虑坝体流变特性情况下的河床断面位移特征值对比。由表5可知，堆石料的流变效应对施工期坝体的变形影响较小，对运行期坝体的变形影响则较大。蓄水运行3 a后河道断面坝体竖向位移的流变变形极值达到20.06 cm，竖向位移较不考虑流变情况下增加了14.0%。水平位移的流变变形极值为30.91 cm，变形增加幅度达到195.1%。由此可见，坝体材料流变效应对坝体各部位变形的影响程度呈现出显著的差异性，且局部流变变形较瞬时荷载变形有大幅度的增加。

表5 河床断面位移特征值对比Table 5 Comparison of characteristic values of displacement of riverbed cross section

4.3.4 面板脱空分析

图14为三板溪面板脱空监测布置图，图15为面板竣工时和蓄水运行3 a后的脱空量等值线图。工程监测报告成果(中国水利水电科学研究院，2016)表明：大坝施工完成时，面板脱空实测最大值为3 cm，出现在①、②期面板施工缝附近；截至2016年底，在M2-2、M2-3、M2-8、M2-9等位置处仍然存在明显的脱空现象，测点处的实测脱空值在2～3 cm之间变化。

图14 面板脱空监测布置示意图Fig.14 Layout of monitoring the disengagement of concrete face slab

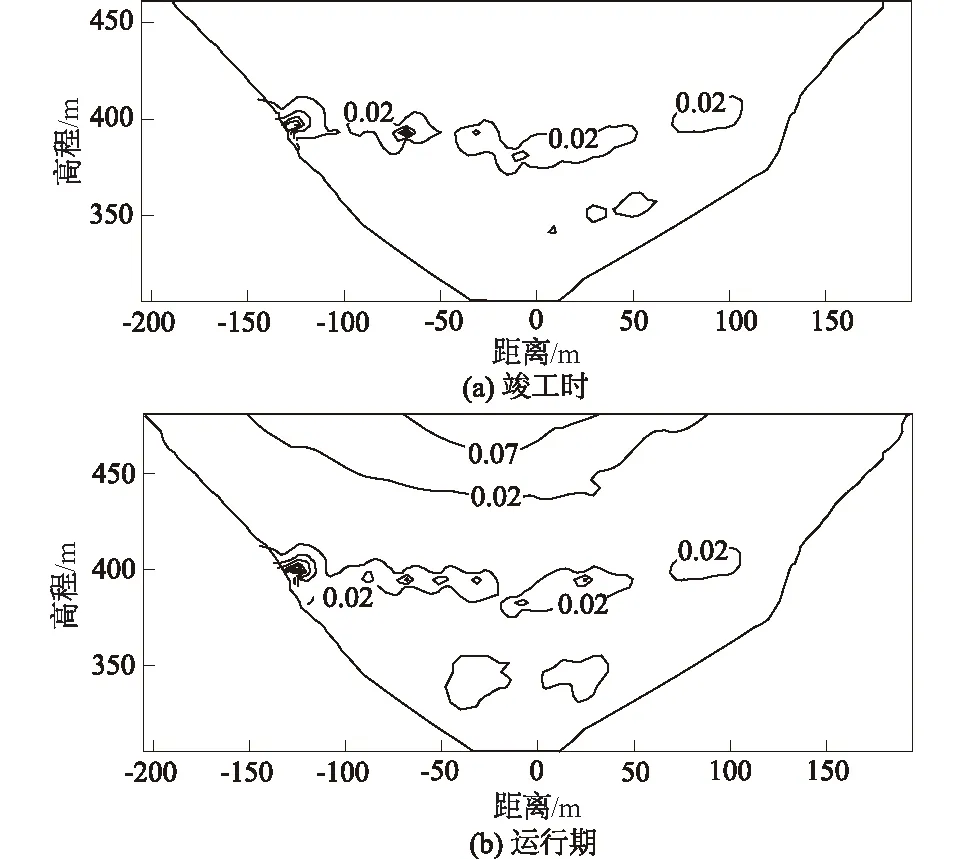
注:等值线上的数值表示面板脱空量(m)。图15 面板脱空量等值线Fig.15 Contour maps of disengaged distance of face slab

计算成果表明：大坝施工完成时，在①、②期面板施工缝附近(高程380～400 m)出现了面板脱空现象，且不同部位的最大脱空值在2～5 cm之间变化；水库蓄水运行3 a后，380～400 m高程处面板的脱空值有所增加，脱空范围的大小也有所扩展。同时，在坝顶部位的面板出现了新的脱空区，脱空范围约7 000 m2，最大脱空值为7 cm。

通过比对分析计算成果与监测成果可知：计算值与实测值基本吻合，三板溪面板堆石坝在施工期和运行期都出现了局部脱空现象。由于面板也采用了分期施工的方式，因此，前期浇筑的面板在后期填筑坝体引起的应力与变形作用下出现脱空现象。运行期的坝顶附近面板产生脱空的主要原因则是坝体后期流变变形与面板变形的不协调所导致。由于数值计算结果中产生最大脱空值的位置处没有布置测点，故根据已知测点脱空值的合理性推测该结果应该是合理的。工程竣工时和运行过程中出现的脱空位置与图15所示的计算脱空位置一致。

2008年1月水下检查结果显示：在高程382～388 m范围(①、②期面板施工缝附近)发生破损。破损长度约184 m、宽度约2～4 m、深度一般在10～25 cm不等，最深40 cm。该破损区分布位置与脱空位置一致，表明脱空与面板破坏之间存在很强的关联性。面板修补治理的同时，还需要采取面板脱空的处理措施，否则面板破坏问题无法得到根本性的解决。

5 结 论

针对三板溪面板堆石坝变形特征及脱空问题，基于堆石坝流变分析理论和接触面模型，提出了面板脱空量值和脱空范围的计算方法。在此基础上研究了三板溪面板堆石坝坝体的空间变形分布特性及其对面板脱空分布特性的影响。主要结论如下：

(1)坝体堆石料的流变效应是导致三板溪坝体后期沉降变形增加的主要因素；坝体空间应力分布的不同导致坝体不同部位的流变变形量也不相同，即流变变形呈现出强烈的非均匀分布特点。

(2)三板溪面板堆石坝的混凝土面板在施工期和运行期都出现了脱空现象，施工期脱空位置位于①期面板与②期面板交界处，脱空值范围为2～5 cm；长期运行后坝顶部位的面板出现了新的脱空区，其脱空值在2～7 cm之间。坝体流变变形是导致运行期坝顶附近面板出现脱空现象的根本原因。