冲击载荷作用下矿柱力学响应特征分析

董川龙，宁掌玄

（山西大同大学 煤炭工程学院，山西 大同 037003）

0 引 言

向深部发展是井工矿的必然发展趋势，深部开采面临着巨大挑战，如典型的“三高一扰动”特征，特别地诸如瓦斯爆炸、冲击低压等灾害频繁发生［1－4］，严重制约着矿山高效发展。 金属矿回采是通过分阶段进行的，在垂直方向上阶段之间通过矿柱隔离，为保证下阶段回采的安全，往往要在矿柱上留有一定厚度的碎石垫层，当采空区围岩发生大面积冒落时，垫层可以起到吸收冲击能和消波的作用［5－9］。 由于矿体采出后存留采空区高度比较大，因而冒落体从采空区顶部滚落到底部具有很高的动能，对矿柱形成强烈的冲击，因此有必要分析矿柱在冲击载荷作用下的力学响应，为防灾提供理论指导。

对于采空区冒落体机械冲击灾害，国内外学者鲜有人研究，但有学者研究了山体落石对结构物（例如棚硐、公路、挡土墙、混凝土梁等）的冲击响应。 何思明等［10］以实际滚石棚洞结构为原型，采用动力有限元对滚石冲击过程进行了数值仿真，研究滚石在不同冲击角度下棚洞结构的动力学响应，为滚石防护工程设计提供理论基础。 刘成清等［11］以钢筋混凝土棚洞为原型，通过ANSYS／LS－DYNA 有限元分析软件，考虑不同能量的落石冲击不同位置的情况下，分析了钢筋混凝土棚洞的动静力响应及其冲击动力系数，得到了弹塑性状态下棚洞冲击动力系数的变化规律。 刘土光等［12］采用能量原理和刚塑性材料本构模型对冲击载荷作用下的矩形加筋板结构的塑性动力响应进行了分析，认为动力响应的变形模态与静力极限变形模态相同。 许斌等［13］利用落锤试验机对一组简支配箍钢筋混凝土梁进行抗冲击性能试验研究，分析了不同冲击锤重、冲击速度和冲击能量及2 次冲击下钢筋混凝土梁的抗冲击行为，采用高速摄像机记录了各试件在冲击过程中裂缝的发生、发展直至破坏的全过程。 叶四桥等［14］选择国内外代表性的5 种冲击力算法，在设定落石尺寸、自由落高和缓冲土层厚度下进行冲击力计算结果的系统对比分析，发现国内有关规范推荐的落石冲击力算法实际计算的是落石冲击过程平均冲击力，而并非最大冲击力，从而导致工程应用中冲击力计算结果严重偏小。 叶四桥、郭绍平等［15－16］通过比对前人研究的落石冲击力计算方法，并结合试验研究，基于冲量定理，引入放大系数的概念，对前人导出的平均冲击力计算公式加以修正。 刘茂［17］以弹塑性修正的Hertz 接触理论为基础，考虑落石冲击缓冲层过程的复杂性和缓冲层厚度的影响，结合路基规范方法的落石冲击深度公式，得出落石最大冲击力计算方法。杨其新等［18］针对我国的工程实际，以若干单一化条件为基础，采用小比尺模拟棚式明洞，通过重锤自由下落到土槽的实验方法，找出落石对具有不同厚度填土缓冲层的明洞产生冲击力的变化规律，提出了计算落石冲击力的实验式，为工程设计提供基本依据。

笔者以东升庙矿11 号矿体＋850 m 水平以上采空区围岩冒落冲击隐患为研究切入点，应用类似的工程方法，建立了围岩大冒落冲击模型，视垫层与矿柱为耦合结构，进一步应用理论分析和数值模拟分析，对矿柱和垫层组合的承载体系在受冲载荷作用下力学响应进行了分析，最后从安全有效、经济合理的角度出发研究了垫层合理的设置厚度。

1 冒落模型和冲击模型的建立

东升庙铜矿位于巴彦淖尔市境内，目前主采2号和11 号矿体（图1），11 号矿体相对2 号矿体规模较小，采后极易形成空间狭小密闭采空区（图2），采空区上部围岩一旦发生冒落，会引发动力冲击灾害，严重威胁矿山的安全生产。

图1 Surpac 三维矿体模型Fig.1 Surpac three－dimensional orebody model

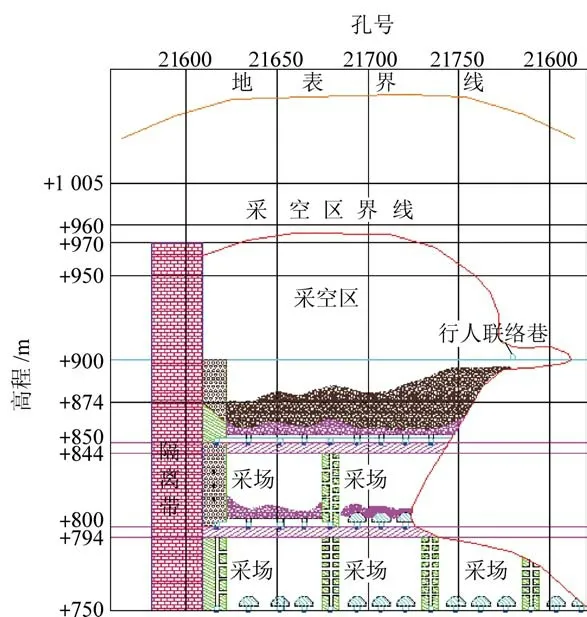
图2 11 号矿体采空区Fig.2 Goaf of No.11 orebody

以东升庙矿11 号采空区为例，虽然目前采空区没有发生整体大冒落的可能性，但随着采动的影响和采空区范围的不断扩大，局部冒落不断进行，冒落体周边很可能发生切应力集中，当围岩切应力大于其抗剪强度时，即会发生大面积垮落。 根据极限自然平衡拱理论，为了能从理论上建立求解公式，将围岩发生大冒落近似为一圆柱体（图3）。

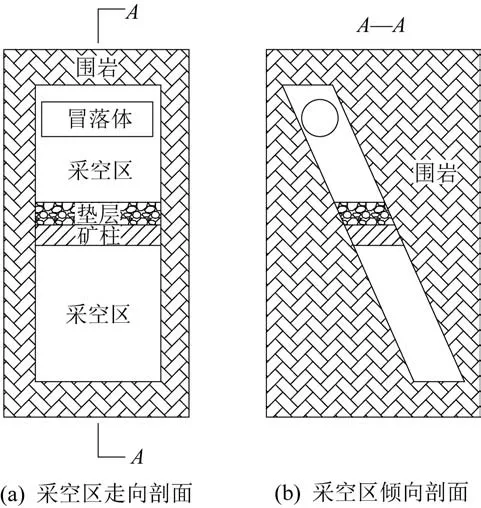
图3 围岩大冒落模型Fig.3 Large caving model of surrounding rock

根据现场试验和调查，得到冒落体力学计算参数（表1）。

表1 冒落体冲击力计算参数Table 1 Calculation parameters of falling impact force

采空区底部结构由2 部分组成：一部分是底柱和顶柱，一部分是覆盖在底柱上部一定厚度的缓冲垫层，垫层材料一般是围岩自然冒落或强制崩落围岩形成的碎石。 由于垫层的缓冲作用，冒落体的冲击力只有部分通过缓冲层传递到底柱和顶柱上。 施加在底柱和顶柱上的冲击载荷与冒落体质量、冲击速度、垫层材料的厚度等因数密切相关，大冒落体与垫层的接触关系如图4 所示。

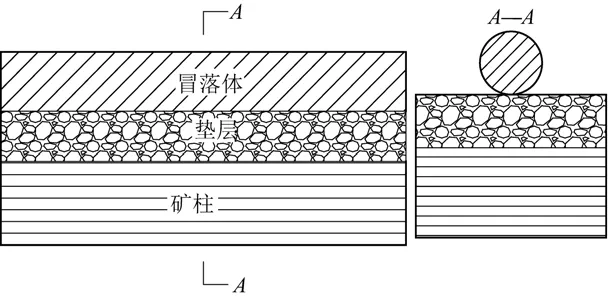
图4 冒落体冲击垫层Fig.4 Falling rock mass impacting cushion

按照材料力学理论，可将受冲矿柱简化为梁结构，根据矿柱两端约束情况不同，矿柱进一步可以简化为简支梁和固支梁（图5）。

图5 梁结构Fig.5 Beam structure

2 冲击基础理论的建立

2.1 冲击特性

将大冒落体简化为一圆柱体，将圆柱体进行分段研究，沿圆柱体长轴方向取单位长度，则可建立大冒落体冲击模型（图6）。

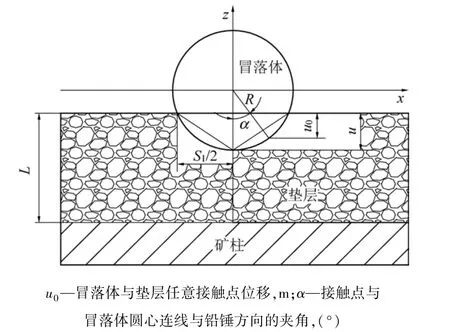
图6 冒落体冲击垫层力学模型Fig.6 Mechanical model of falling rock mass impacting cushion

根据文献［19］，应用动量定理、弹性力学理论、运动学理论，可得出冒落体对垫层的最大冲击力以及与此相对应冒落体在垫层中的位移。

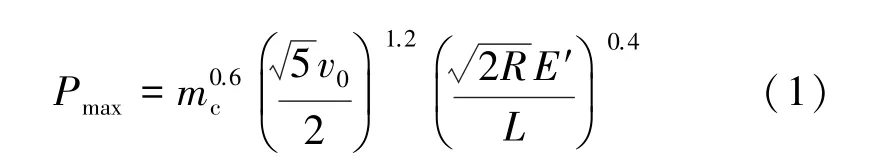
式中，Pmax为冒落体对垫层的最大冲击力，N；v0为冒落体撞击垫层的初始速度，m／s；R为冒落体横截面圆半径，m；E′ 为垫层的变形模量，Pa；L为垫层厚度，m；mc为单位长度冒落体的质量，kg。

式中，u为冒落体对垫层最大冲击时在垫层中的位移，m。

参考文献［26］，根据应力扩散理论，可以得出冲击载荷通过垫层均布载荷分散到矿柱上的长度范围。

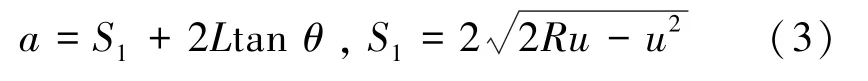
式中，a为施加在矿柱上的冲击压力分布长度，m；S1为冲击力最大时冒落体与垫层的水平接触部分长度，m；θ为应力扩散角，θ＝45°－（φ／2） ；φ为碎石垫层的内摩擦角，（°）。

作用在矿柱上的分布载荷为

式中，q为作用在矿柱上的分布载荷，Pa。

2.2 矿柱简化为梁

2.2.1 矿柱简支梁理论

对矿柱和垫层进行受力分析（图7）。

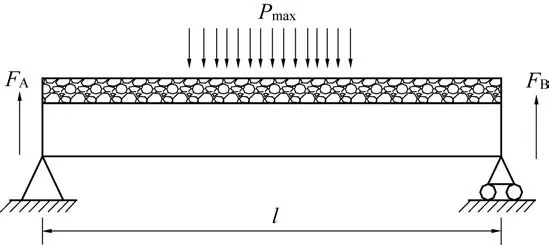
图7 矿柱和垫层受力分析Fig.7 Force analysis of pillar and chshion

根据散体材料应力扩散效应，作用于垫层上的载荷经过垫层应力扩散后，分布于矿柱上载荷范围大于直接分布于垫层上的载荷范围，又根据实际分析，在矿柱宽度方向上，冒落体尺寸基本接近于矿柱横向尺寸，因此可分析冲击载荷经垫层扩散作用后沿矿柱全宽度方向均匀分布（图8）。

根据材料力学理论，按图8 简支梁受力情况，可求得矿柱内最大剪应力、最大正应力、最大挠度。

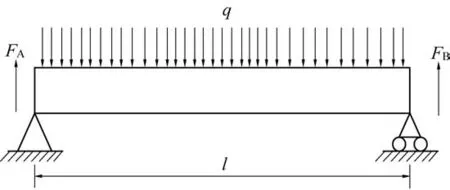
图8 矿柱受力分析Fig.8 Force analysis of pillar

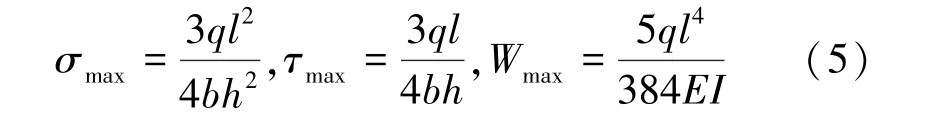
式中，σmax为矿柱内最大正应力，Pa；τmax为矿柱内最大剪应力，Pa；Wmax为矿柱最大挠度；b，h，l为矿柱的宽度、高度和长度，m；E为矿柱的弹性模量，Pa；I为矿柱矩形截面惯性矩，m4。

2.2.2 矿柱固支梁理论

对矿柱和垫层进行受力分析（图9 中M为力矩，FA、FB为支座反力）。 类似简支梁，同理对矿柱单独受力分析（图10）。

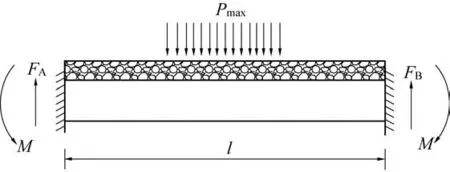
图9 矿柱和垫层受力分析Fig.9 Force analysis of pillar and chshion

图10 矿柱受力分析Fig.10 Force analysis of pillar

根据材料力学理论，按图10 固支梁受力情况，可求得矿柱内最大剪应力、最大正应力、最大挠度。

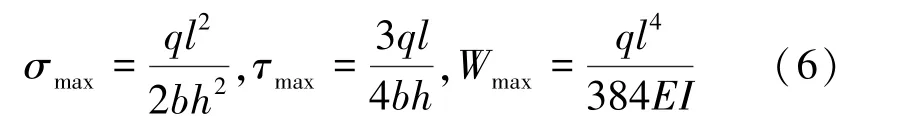
2.3 垫层厚度与矿柱力学响应量的关系

按静力等效原理，取单位长度圆柱体做研究，根据上述理论，可导出矿柱内最大正应力、最大剪应力、最大挠度与垫层厚度间的关系。

1）简支梁情况。

2）固支梁情况。

3 工程算例分析

3.1 矿柱和垫层力学响应分析

将已知条件：v0＝31 m／s，R＝6.4 m，E′ ＝60 MPa，mc＝378 126.336 kg 代入式（1）、式（2），可得冒落体对垫层最大冲击力以及此时冒落体在垫层中的位移随垫层厚度变化规律（图11）。

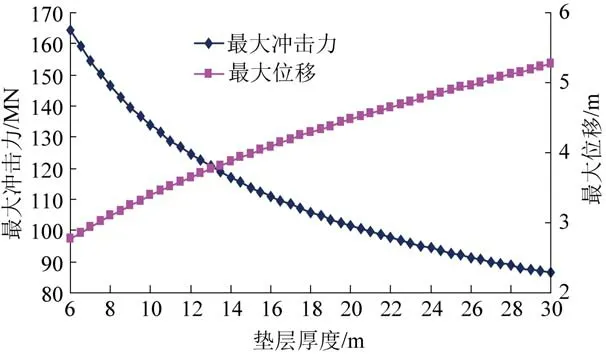
图11 冒落体最大冲击力、位移随垫层厚度变化规律Fig.11 Variation of maximum impacting force and displacement with thickness of cushion

由图11 可以看出，最大冲击力随垫层厚度增加逐渐减小，垫层厚度从最小6 m 变化到最大30 m，最大冲击力从164.363 05 MN 降低到86.340 824 MN，总降幅约78.022 226 MN，垫层厚度在6 ～15 m变化时，冲击力随垫层厚度增大降幅比较大，垫层厚度每增加0.5 m，冲击力降低约为1.5～5.0 MN，垫层厚度在15～30 m 变化时，冲击力随垫层厚度增大降幅比较小，垫层厚度每增加0.5 m，冲击力降低为0.5～1.5 MN。

由图11 可以看出，对应于最大冲击力时冒落体在垫层中的位移随垫层厚度增大逐渐增大，垫层厚度从最小6 m 变化到最大30 m，冒落体在垫层中的位移从2.763 542 m 增大到5.260 828 m，总增幅约为2.497 286 m，垫层厚度在6～20 m 变化时，冒落体在垫层中的位移随垫层厚度增大增幅较大，垫层厚度每增加0.5 m，位移增加0.05 ～0.09 m，垫层厚度在20～30 m 变化时，冒落体在垫层中的位移随垫层厚度增大增幅较小，垫层厚度每增加0.5 m，位移增加0.03～0.05 m，冒落体对应于各厚度垫层的位移均小于冒落体半径6.4 m。

将已知条件：v0＝31 m／s，R＝6.4 m，E′ ＝60 MPa，mc＝37 8 126.336 kg，l＝16.87 m，h＝14 m，θ＝35°，E＝28 GPa，I＝228.666 666 7 m4代入式（7）、式（8），可得简支梁和固支梁情况下矿柱在冲击载荷作用下内部最大正应力、最大剪应力、最大挠度随垫层厚度变化规律（图12、图13）。

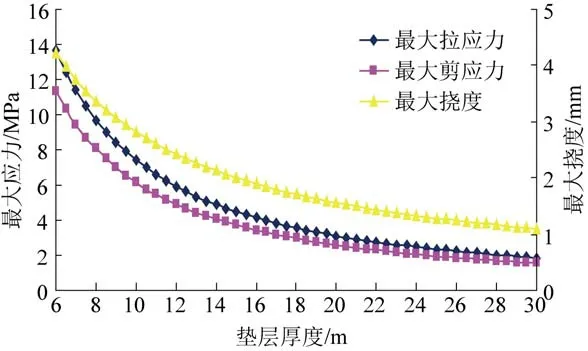
图12 简支矿柱力学响应规律Fig.12 Mechanical response of simply supported beam

图13 固支矿柱力学响应规律Fig.13 Mechanical response of clamped beam

由图12 可以看出，矿柱内最大正应力随垫层厚度增大而逐渐减小，垫层厚度从最小6 m 增大到30 m，正应力从13.657 22 MPa 减小到1.860 804 MPa，总降幅约为11.796 416 MPa。 垫层厚度在6 ～18 m 变化时，正应力随垫层厚度增加降幅较明显，垫层厚度每增加0. 5 m， 正应力降低0. 13 ～1.23 MPa；垫层厚度在18 ～30 m 变化时，正应力随垫层厚度增加降幅较小，垫层厚度每增加0.5 m，正应力降低0.04～0.13 MPa。

由图12 可以看出，矿柱内最大剪应力随垫层厚度增大而逐渐减小，垫层厚度从最小6 m 增大到30 m，剪应力从11.333 79 MPa 减小到1.544 235 MPa，总降幅约为9.789 555 MPa。 垫层厚度在6 ～20 m 变化时，剪应力随垫层厚度增加降幅较明显，垫层厚度每增加0.5 m，剪应力降低0.08 ～1.02 MPa；垫层厚度在20 ～30 m 变化时，剪应力随垫层厚度增加降幅较小，垫层厚度每增加0.5 m，剪应力降低0.03～0.08 MPa。

由图12 可以看出，矿柱内最大挠度随垫层厚度增加而逐渐减小，垫层厚度从最小6 m 增大到30 m，挠度从4.229 857 mm 减小到1.097 114 mm，总降幅约为3.132 743 mm，垫层厚度在6～17 m 变化时，挠度随垫层厚度增加降幅较明显，垫层厚度每增加0.5 m，挠度减小0.05 ～0.26 mm，垫层厚度在17 ～30 m变化时，挠度随垫层厚度增加降幅较小，垫层厚度每增加0.5 m，挠度减小0.02～0.05 mm。

由图13 可以看出，矿柱内最大正应力随垫层厚度增大而逐渐减小，垫层厚度从最小6 m 增大到30 m，正应力从9.104 814 MPa 减小到1.240 536 MPa，总降幅约为7.864 278 MPa。 垫层厚度在6 ～18 m变化时，正应力随垫层厚度增加降幅较明显，垫层厚度每增加0.5 m，正应力降低0.09 ～0.82 MPa；垫层厚度在18～30 m 变化时，正应力随垫层厚度增加降幅较小，垫层厚度每增加0.5 m，正应力降低0.03 ～0.09 MPa。 由于固支梁与简支梁最大剪应力相同，此处不再赘述。

由图13 可以看出，矿柱内最大挠度随垫层厚度增加而逐渐减小，垫层厚度从最小6 m 增大到30 m，挠度从0.845 971 mm 减小到0.219 423 mm，总降幅约为0.626 548 mm。 垫层厚度在6 ～17 m 变化时，挠度随垫层厚度增加降幅较明显，垫层厚度每增加0.5 m，挠度减小0.009 ～0.051 mm；垫层厚度在17～30 m 变化时，挠度随垫层厚度增加降幅较小，垫层厚度每增加0.5 m，挠度减小0.003～0.009 mm。

比较图12 和图13 发现，垫层厚度相同时，矿柱简化为固支梁最大正应力比简化为简支梁最大正应力要小，2.228 976 ～0.620 268 MPa；垫层厚度相同时，矿柱简化为固支与简支梁最大剪应力相同；垫层厚度相同时，矿柱简化为固支梁最大挠度比简支梁最大挠度要小3.383 886～0.877 691 mm。

3.2 合理厚度垫层分析

从经济节约的角度出发，分析图11—图13 发现，并不是垫层设置得越厚越好，应有一个经济合理的设置厚度。 垫层厚度为20 ～30 m 时，最大冲击力、最大拉应力、最大剪应力随垫层厚度增加减小幅度很小，因此垫层厚度不宜超过20 m。 根据式（3）和（4），垫层越厚冒落体对矿柱形成的冲击载荷q越小，对矿柱稳定性越有利，但是由图11 中可以看出，垫层厚度为20 ～30 m 时，冒落体在垫层中的位移随垫层厚度增加增幅很小，因此垫层设置厚度不宜超过20 m。

从安全有效的角度出发，为保证矿柱有足够的稳定性，垫层的设置厚度必须保证矿柱受冲击载荷作用下其最大正应力、最大剪应力不超过矿柱岩体的抗拉强度和抗剪强度，保证矿柱受冲击载荷作用下最大挠度不超过一定限值。 矿柱简化为简支梁的情况下：由图12 可以看出，当垫层厚度取18 m 时，矿柱最大拉应力为3.568 983 MPa，此时该拉应力小于矿柱岩体的抗拉强度3.6 MPa，即可取垫层厚度为18 m；当垫层厚度取12.5 m 时，矿柱内最大剪应力为4.668 731 MPa，此时该剪应力小于矿柱岩体抗剪强度4.7 MPa，即可取垫层厚度为12.5 m。 矿柱简化为固支梁的情况下：由图13 可以看出，当垫层厚度取13 m 时，矿柱最大拉应力为3.572 917 MPa，此时该拉应力小于矿柱岩体的抗拉强度3.6 MPa，即可取垫层厚度为13 m；矿柱简化为简支梁和固支梁两种情况时，最大剪应力随垫层厚度变化规律一致，即矿柱简化为固支梁可取垫层厚度为12.5 m。

综合考虑影响矿柱稳定性的临界失稳状态指标，为保证矿柱在冒落体冲击载荷作用下有足够的强度，结合设置垫层厚度经济节约的原则，可以考虑设置厚度18 m 左右的垫层。

3.3 垫层设置厚度数值模拟分析

根据现场工程地质条件，将问题简化为平面应变问题，为保证开挖区域不受边界约束条件的影响，可取矿体厚度3 ～5 倍的区域进行建模，因此，所建模型长度取90 m，阶段高度50 m，矿柱高度和跨度分别为14、17 m，模型高度视垫层厚度情况而定，左右边界和底边界为固定边界，上边界为自由边界，为跟理论计算结果相对应比较，选取监测点1 和2 对矿柱最大拉应力和剪应力进行监测，简化模型如图14 所示，所赋物理力学参数见表2。

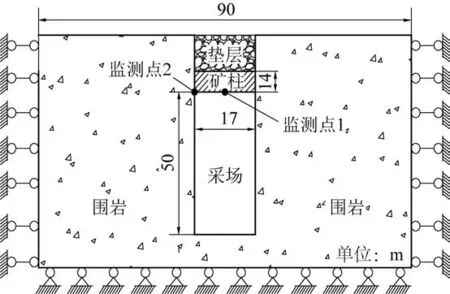
图14 简化模型Fig.14 Simplied model

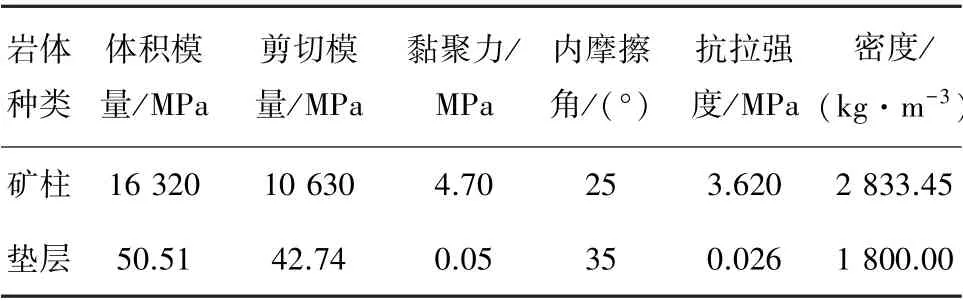
表2 矿岩物理力学参数Table 2 Physical and mechanical parameters of ore and rock

根据式（1）、（2）计算出各垫层厚度下对应冲击均布载荷，取1 m 垫层厚度增幅，将冲击载荷逐级加载到垫层上部，可得出矿柱受冒落体冲击载荷作用下内部应力随垫层厚度变化规律以及矿柱塑性区分布状况（图15 和图16）。

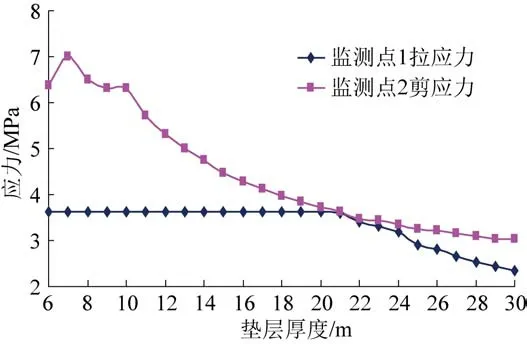
图15 矿柱内应力随垫层厚度变化规律Fig.15 Variation of stress in pillar with cushion thickness

由图15 可以看出，矿柱内剪应力总体上随垫层厚度增加逐渐减小，且其降低幅度随垫层厚度增加也呈现逐渐减小的趋势，当垫层厚度增大到15 m，矿柱内最大剪应力为4.474 MPa，开始小于抗剪强度4.7 MPa。 由于数值模型采用莫尔－库仑模型，即矿柱内应力一旦达到抗拉强度，便产生屈服，应力保持在3.6 MPa 左右，当垫层厚度达到21 m，矿柱内最大拉应力为3.586 MPa，开始小于抗拉强度3.6 MPa，因此，垫层厚度小于21 m，拉应力水平基本维持在3.6 MPa，垫层厚度大于21 m，拉应力随垫层厚度增加逐渐减小。

限于篇幅，图16 仅列出部分典型垫层厚度情况下矿柱内塑性区分布状况，其中蓝色代表没有塑性区，其他颜色为塑性破坏区。 由图16 可以看出，随垫层厚度增大矿柱两端和底部塑性区连通性和面积不断减小，逐渐过渡到稳定状态。 垫层厚度达到18 m，矿柱两端贯通塑性区消失，底部塑性区表现出面积较小的成拱稳定状态，垫层厚度达到22 m，矿柱底部塑性区完全消失，仅矿柱上端与围岩连接处表现出较小范围塑性区。

图16 矿柱内塑性区分布状况Fig.16 Distribution of plastic zone in pillar

综合上述分析，从矿柱内最危险点应力状态确定垫层厚度为21 m，比理论计算结果18 m 稍大，在工程误差范围内允许，且说明数值模拟结果偏于安全；从矿柱塑性区分布形态来看，垫层厚度达到18 m，矿柱两端和底部没有形成大范围贯通塑性区，仅上端与围岩连接处以及底端产生小范围塑性区，这在工程上是允许的。 从实际分析出发，保证矿柱内每一点都不发生屈服的条件比较苛刻，因此，可以矿柱塑性区分布形态的稳定性作为设置垫层厚度的判别标准，最终确定设置厚度18 m 垫层可确保矿柱在冲击载荷下不发生失稳。

4 结 论

1）冒落体对垫层的最大冲击力、矿柱内部应力以及挠度均随垫层厚度增加而减小，且减小幅度随垫层厚度增加逐渐减小，垫层厚度较小的情况下衰减幅度较大；矿柱分别简化为简支梁和固支梁情况下，确定垫层厚度分别为18 m 和13 m，数值模拟结果更接近于简支梁情况，综合数值模拟和理论分析，最终确定垫层的合理设置厚度为18 m 左右。

2）基于材料力学理论和静力等效原理，采用梁结构作为简化的力学模型，对矿柱受冲击载荷作用下力学响应进行了分析，其中没有考虑矿柱实际三维尺寸以及矿柱受震动冲击的影响。 为了能使力学模型更加接近工程实际，未来有必要基于弹性力学理论寻求更加合理的受冲板力学模型来对矿柱受冲击载荷作用下力学响应进行分析。