岩-土交界面处超大直径过江盾构隧道地震响应特征

姚二雷，刘志芳，苗 雨

(1.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010； 2.华中科技大学 土木工程与水利学院，武汉 430074)

1 研究背景

1995年阪神地震中，神户市大开地铁车站的严重破坏表明现有的地下结构并不安全，有时甚至会发生严重破坏[1-2]。由此，国内外专家学者展开了对地下结构的一系列研究。Bao等[3]采用土-水完全耦合的有限元-有限差分方法，研究了可液化场地中大型矩形地铁隧道的抗震性能，结果表明在工程实践中注浆加固法是减轻结构上浮的重要方法。Chen等[4]采用数值方法揭示出隧道中由地震引起的应力与隧道埋深和地震波波长密切相关。Yu等[5]对汶川地震中受损严重的陇西隧道进行了震害调查，发现距离断层较远的隧道出现轴向和横向裂缝，而距离断层较近的隧道完全坍塌。王国波等[6]进行了多孔交叠地铁隧道的地震响应分析。殷允腾等[7]分析了地震灾害来临时隧道结构在土岩软硬结合部位的破坏机理及相关抗震措施。崔光耀等[8]通过汶川公路隧道的三维有限差分数值模拟和现场典型震害分析探明了软硬围岩交接普通段隧道震害机制，即震害主要发生在软硬围岩交接段软岩部分。王维[9]对软硬突变地层中盾构隧道的地震响应特征进行了研究，发现在软硬地层交界处，隧道结构的应力会发生突变。姚二雷等[10]通过数值方法研究了纵向不均匀场地内弯折隧道的地震响应特征，计算结果表明相对于直线隧道，弯折隧道的截面弯矩较小，而截面剪力较大；隧道内的应力主要集中在不均匀场地交界处，且拉压应力带与隧道轴线大体呈45°。

本文以武汉市三阳路超大直径“公铁合建”过江盾构隧道工程为依托，对其处于软硬交界土层中的隧道断面进行了二维地震响应分析。探究了该模型在强震作用下衬砌损伤演化规律、衬砌响应包络特征，上述研究成果对提高该类盾构隧道结构抗震性能的认识及其抗震设计水平提供了参考和借鉴。

2 工程概况

武汉三阳路长江隧道工程(武汉轨道交通7号线一期工程)规划定位为城市道路与轨道交通共用的“公铁合建”过江通道工程。该隧道采用直径15.76 m的超大型泥水平衡盾构施工，为“国内第一，世界第三”超大直径盾构隧道工程。江中段部分隧道处于砂土层与岩石层交界面。穿越不同土层可能对该处隧道的抗剪性能、位移响应等具有较大影响。因此，以岩-土交界面处的盾构隧道断面为研究对象进行了一系列抗震分析,为其抗震设计提供依据。

3 有限元模型

3.1 模型概况

基于大型通用有限元软件ABAQUS中的Explicit计算平台，建立了双盾构隧道-土体模型。根据楼梦麟等[11-12]的研究，当取整个场地有限元模型的宽度大于结构宽度的5倍时，地基两侧的边界对结构动力反应的影响基本消失。因此，模型尺寸为300 m×80 m(长×宽)。隧道衬砌外径为15.2 m，内径为13.9 m，上覆土层厚度为37.4 m，两隧道间距为6 m，隧道周围1.5 m范围内设置注浆加固区。衬砌内部构件及相应尺寸为：衬砌内公路板厚0.53 m，长13.9 m；竖向隔板厚0.35 m，长约6 m。衬砌及其内部构件的本构采用C50混凝土损伤塑性模型，其模型参数取值见表1—表3，Davidenkov模型参数见表4。

表1 混凝土损伤塑性模型参数Table 1 Parameters of concrete damage plasticity model

表2 混凝土受压屈服应力、损伤因子与相应的非弹性应变Table 2 Compressive yield stress, damage factor, and corresponding inelastic strain of concrete

表3 混凝土受拉屈服应力、损伤因子与相应的开裂应变Table 3 Tensile yield stress, damage factor, and corresponding crack strain of concrete

表4 Davidenkov模型参数Table 4 Parameters of Davidenkov model

混凝土弹性模量为34.5 GPa，泊松比为0.2，密度为2 500 kg/m3。根据地质勘察报告，模型土体分为两层，上层为砂土，厚度为51.56 m；下层为风化基岩，厚度为28.44 m，岩土层分布示意如图1所示。砂土密度为1 980 kg/m3，泊松比为0.2；基岩密度为2 200 kg/m3，泊松比为0.4。

图1 岩土层分布示意图Fig.1 Sketch of distribution of rock and soil layers

采用修正的Davidenkov黏弹性动力本构模型模拟土的动力特性[13]，该模型的表达式为

(2)

式中：τoct和γoct分别为八面体上剪应力和剪应变；τoct,c和γoct,c分别为八面体上剪应力-剪应变滞回曲线加卸载转折点对应的剪应力和剪应变幅值，上述参数由ABAQUS主程序计算获得；Gmax为土体最大动剪切模量，由土样共振柱试验中测得；τoct,ult为剪应力上限值，由土样共振柱试验中测得的最大动剪应变和对应的动剪切模量计算确定；H为中间变量；γ为主程序自动计算所得剪应变；A、B及γ0基于土样的共振柱试验及式(2)获得。

地基土-盾构隧道体系有限元模型如图2所示。地基土与隧道结构均采用平面应变单元，最大单元尺寸为1.5 m。为提高计算效率，衬砌与土体间采用绑定(Tie)约束，即不考虑二者之间的相对运动。同时，为简化计算并定性分析岩-土交界面处盾构隧道的损伤演化规律及地震响应特征，未考虑衬砌及其内部构件的配筋。

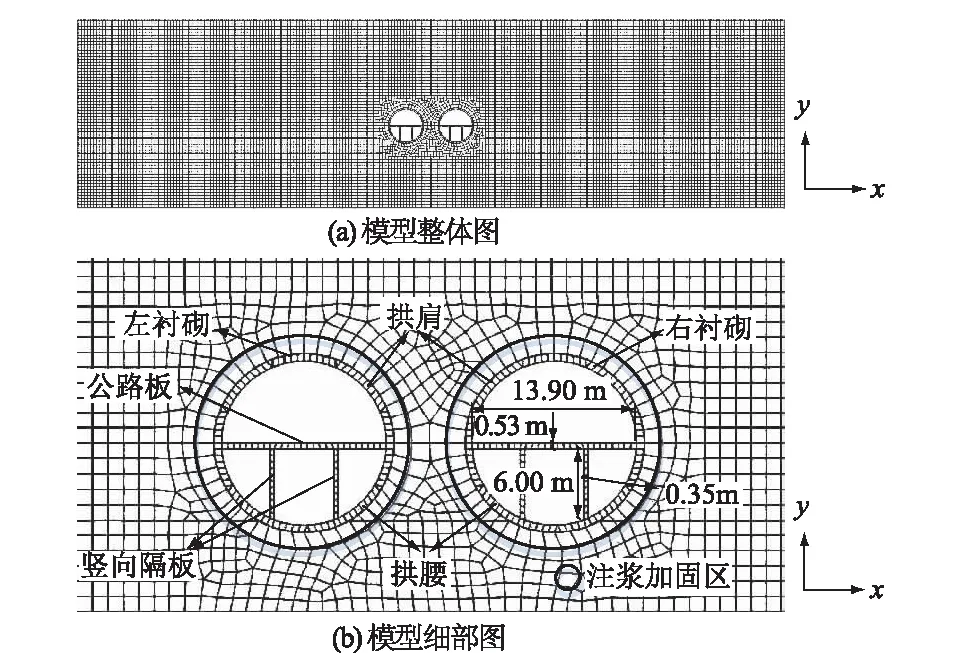
图2 地基土-盾构隧道模型二维有限元网格Fig.2 Two-dimensional finite element meshes of soil-shield tunnels model

3.2 地震波输入及边界条件

由于武汉市缺少实际地震记录，难以选取震级及震中距相近的天然地震波。汕头海底人工波为一条强震时程，频率分布范围较广，且合成背景与本文工程背景相近(均为水下基岩地震波)，因此地震波选取汕头海底人工波并在水平和竖直两方向输入，其水平分量加速度峰值为0.2g，竖向分量峰值为0.15g。该人工波加速度时程和傅立叶幅值谱分别如图3和图4所示。另外，为探究衬砌及内部构件在不同峰值加速度情况下的响应变化，将该人工加速度时程水平分量峰值调整为0.3g和0.4g，相应的将竖向分量峰值调整为0.2g和0.26g分别计算，计算工况汇总于表5。模型四周均为自由边界。

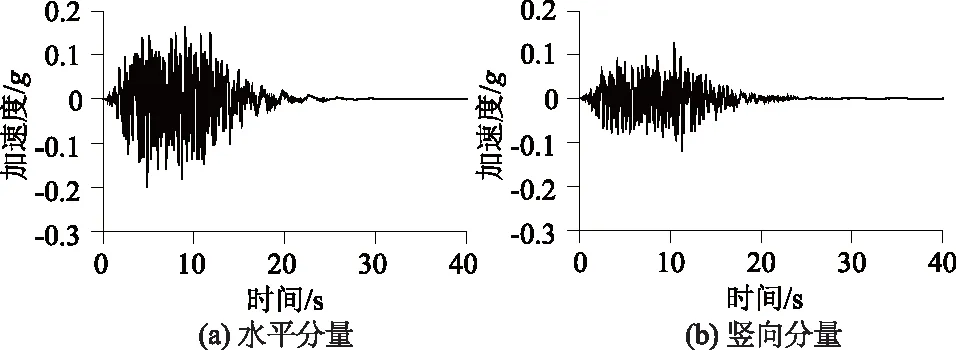
图3 汕头海底人工波加速度时程Fig.3 Acceleration of artificial earthquake wave at the bottom of the sea at Shantou

图4 汕头海底人工波傅立叶幅值谱Fig.4 Fourier amplitude of artificial earthquake wave at the bottom of the sea at Shantou

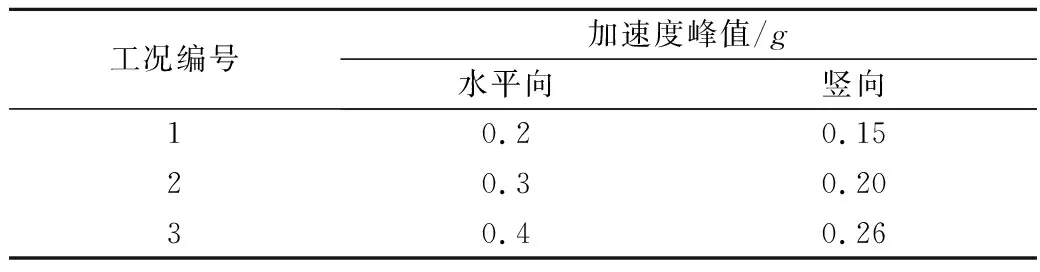
表5 计算工况Table 5 Computational working conditions

4 地震动力响应分析

4.1 衬砌损伤演化过程

首先，分析了各峰值加速度下，左、右两衬砌的震后受拉损伤因子dt(DAMAGET)值的分布，如图5所示。dt介于0～1之间，用于衡量混凝土构件的损伤程度；当dt>0时，混凝土开始出现拉伸裂缝；当dt接近1时，混凝土几乎完全丧失抗拉强度和沿裂缝方向的抗剪强度[1]，即退出工作。其中，0.2g峰值下右侧隧道的损伤因子为0。从图5可以看出，各峰值下受拉的损伤的分布范围基本相同，主要集中在衬砌的拱肩及拱腰位置。在0.2g峰值下左侧衬砌损伤较小，而当峰值为0.3g和0.4g时局部衬砌已几乎完全退出工作。

图5 衬砌受拉损伤因子分布Fig.5 Distribution of tension damage factors of tunnel lining

为了说明岩-土交界面处隧道结构的震害发生机制及其地震破坏的演化过程，以0.4g峰值的数值分析结果为例，输出了几个关键时刻隧道结构混凝土拉伸损伤因子dt值分布云图，如图 6 所示。

图6 衬砌受拉损伤因子分布云图Fig.6 Contours of tension damage factors of tunnel lining

当t=3.15 s时，右侧衬砌的右拱腰处首先出现拉伸裂缝并已贯穿整个截面，基本丧失抗拉强度和水平向抗剪强度，同时在左侧衬砌的右拱腰出现了轻微裂缝；当t=6.10 s时，两衬砌的左拱腰和右拱肩几乎同时出现受拉裂缝且左拱腰处的裂缝迅速发展，其损伤数值已超过右拱腰的损伤数值；当t=11.40 s时，右侧衬砌的两拱腰以及左侧衬砌的左拱腰已几乎退出工作，而两衬砌的拱肩裂缝发展较为缓慢，仍有一定的承载能力；当t=13.00 s时，右侧衬砌的公路板—竖板节点以及公路板—衬砌节点均出现贯穿裂缝，左侧衬砌的公路板—衬砌左节点也已基本破坏。当t=13.95 s时，两衬砌的右拱肩处拉伸裂缝几乎同时贯通，至此，因拱肩、拱腰均出现贯穿裂缝，衬砌已完全失去承载能力、无法再保障交通线路的安全运营，因而失效。

综上，衬砌的破坏始于拱腰位置的受剪破坏；拱腰破坏后，竖板上下相对位移加剧，导致节点破坏；拱肩处裂缝发展较慢，破坏时刻相对滞后。另外，衬砌拱腰处的破坏区域均在岩-土交界面附近的软土层中，处于岩层中的衬砌以及砂土层中的拱顶未见破坏，因此建议对岩-土交界处以及附近的软土层中的衬砌进行加固处理。

4.2 衬砌地震响应

以左侧衬砌为例， 探讨了不同加速度峰值情况下， 岩-土交界处衬砌地震响应特征。 由于相对于水平方向的响应， 竖向响应均较小， 因此这里仅针对水平方向响应进行分析讨论。 衬砌水平加速度响应包络、 水平位移响应包络如图7所示。 从图7可以看出， 由于软、 硬场地的地震响应不同， 各加速度峰值情况下， 衬砌下部加速度响应较大， 上部较小， 而位移包络图呈现出完全相反的规律。 这一现象造成了各包络曲线在拱腰位置均出现突变。 因此， 该处的水平剪应力较大， 是影响隧道抗震安全的重要因素。

图7 各工况下衬砌水平加速度和位移响应包络Fig.7 Envelopes of horizontal acceleration and displacement response of lining in different cases

图8给出了各工况下加速度峰值时刻的衬砌水平剪应力(S11)。曲线显示在150°与330°位置剪应力较大，而在30°及210°位置出现了明显的“捏拢”。加之在水平向地震作用下，衬砌处于左-右椭圆化变形的循环中，因此衬砌两侧的拱肩及拱腰位置均可能承受较大的剪应力。为进一步说明岩-土交界对衬砌剪应力的影响，给出了0.2g情况下衬砌的水平剪应力的包络，如图9所示。图9中显示剪应力在拱腰位置最大，拱肩次之。综上，衬砌拱腰与拱肩处剪应力水平均较高，均可能出现严重破坏，这与4.1节所得结论一致。

图8 加速度峰值时刻衬砌水平剪应力响应包络Fig.8 Envelopes of horizontal shear stress response of lining corresponding to peak acceleration in different cases

图9 0.2g下衬砌水平剪应力响应包络Fig.9 Envelopes of horizontal shear stress response of lining under 0.2g acceleration

另外，图7中显示响应包络线在拱侧位置均出现了一定的“捏拢”；图9也出现了剪应力水平由拱肩(腰)到拱侧逐渐降低的现象。这是由于衬砌内部公路板的存在限制了衬砌的变形，起到了支撑与限制的作用。

5 结 论

本文以武汉三阳路超大直径过江“公铁合建”盾构隧道工程为背景，对其岩-土交界面处的隧道断面进行了二维地震响应分析。结果表明：

(1)在岩-土交界面处附近的软土层中，衬砌会出现明显的受拉损伤，在峰值加速度为0.2g的地震动作用下，该处衬砌处于带裂缝工作状态并未完全破坏，而在0.3g及0.4g情况下，衬砌拱肩及拱腰位置均出现了较大受拉损伤，退出工作。

(2)岩-土交界面处隧道结构的破坏始于拱腰退出工作，进而导致内部构件节点破坏，最终拱肩处拉伸裂缝贯通，导致结构失效。

(3)由于衬砌拱腰处的破坏区域均在岩-土交界面附近的软土层中，建议对岩-土交界处以及附近的软土层中的衬砌进行加固处理。

(4)加速度响应、位移响应在岩-土交界面附近会出现明显的突变。

(5)衬砌内部公路板的存在使超大直径衬砌拱侧的水平剪应力明显减小，起到了支撑和约束作用。