水利水电工程锚固支护监测布置优化分析

任大春，王亚军，段 杭

(1.中国三峡建工(集团)有限公司，四川 凉山 615421； 2.浙江海洋大学 海洋工程装备学院，浙江 舟山 316022)

1 研究背景

目前，锚杆和锚索支护已成为保证水利水电工程边坡及洞室稳定的最主要措施之一。为反映支护受力效果，通常会代表性地选择一定数量的锚杆和锚索安装仪器监测其受力状况，相关行业4个规范[1-4]对监测锚杆锚索布置数量和比例要求有一定差异。因此，需要研究大型水利水电工程中监测锚杆锚索布置的合理标准，用以提升监测工作水平，指导工程施工。

本文分析了国内相关规范规程对监测锚杆锚索的具体数量要求，收集统计了国内部分大型水利水电工程中各建筑物支护工程中监测锚杆锚索的数量情况，并与规范规程进行了对比分析，应用数理统计理论分析监测数据误差与监测数量之间的关系，提出监测锚杆锚索数量的确定原则，为大型水利水电工程监测锚杆锚索的布置提供了依据，也可以在其他工程和其他监测仪器的选择时参考使用。

国内相关设计规范及安全监测规范明确指出，需要采用锚杆应力计和锚索测力计来监测支护锚杆应力和锚索荷载，但2005年以前的安全监测规范均没有直接规定需要采取的锚杆应力计和锚索测力计数量。自2006年以后，一些规范开始明确提出需要监测的锚杆和锚索数量，但各规范要求的锚杆监测最小比例为3‰～5%，相差较大；要求的锚索监测最小比例为3%～5%，也有一定的差距。

(1)《水利水电工程边坡设计规范》(SL 386—2007)[1]指出预应力锚固力的锚杆监测数量应不小于预应力锚杆总数的5%，1 级、2 级边坡预应力锚杆监测数量不宜少于3根，应重点布设在地质复杂部位。

(2)《混凝土坝安全监测技术规范》(SL 601—2013)[2]指出锚杆监测宜选择有代表性的部位按锚杆的形式进行抽样，监测数量占锚杆总数的3%～5%。每根锚杆宜布置1～3个测点，仪器采用锚杆应力计。

预应力锚索监测宜按锚索吨位进行抽样，监测数量占预应力锚索总数的3%～5%，每个典型地质地段或每种锚索应监测2～3根，监测仪器宜采用锚索测力计。

(3)《水电水利工程边坡设计规范》(DL/T 5353—2006)[3]指出在边坡治理中采用了预应力锚杆(索)，应布置锚杆(索)测力计(预应力传感器)监测，其数量不得少于总根数的5%。

(4)《混凝土坝安全监测技术规范》(DL/T 5178—2016)[4]指出锚杆应力监测宜选择有代表性的部位和各种形式的锚杆抽样进行。每根监测锚杆宜布置1～3个测点，监测仪器采用锚杆应力计。监测数量应根据实际需要确定，宜不低于总量的3‰。

预应力锚索监测宜对各种吨位、长度的锚索抽样进行；监测仪器宜采用锚索测力计；监测数量宜不低于总量的5%，且不少于3根。

由上述分析可知，各规范对支护锚杆和锚索的监测仪器布置有较大差距，需要进一步的分析研究。

2 锚杆锚索监测情况调研

为了解监测锚杆(索)在大型水利水电工程中的应用情况，特别是监测锚杆(索)的应用比例，特选取国内10个有代表性的大型水利水电工程进行应用情况调查，统计工程中采用的锚杆、锚索数量和相应的监测锚杆、锚索，以总结经验并提出问题，10个工程大坝的基本参数详见表1。

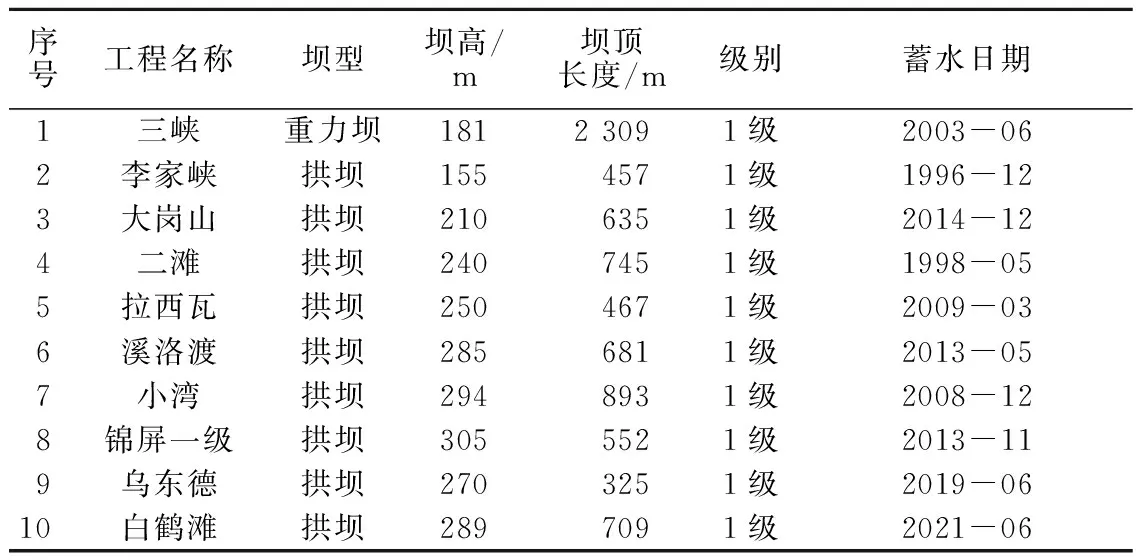
表1 典型混凝土坝基本参数Table 1 Basic parameters of typical concrete dams

2.1 监测锚杆比例

10个大型水利水电工程锚杆监测应用情况调研结果见表2和表3。从各工程监测锚杆比例区间案例数看，监测锚杆比例<0.3%的占比达73.9%，>0.5%的仅占21.7%,其中仅有两例的监测锚杆比例>1%，没有发现监测锚杆比例>5.0%的案例。说明大多数情况下，监测锚杆的比例不满足规范中0.3%～5.0%之间的要求。

表2 国内水电工程主要部位监测锚杆比例统计Table 2 Proportion of monitoring anchor bolts in main parts of hydropower projects in China

表3 监测锚杆数量比例分布Table 3 Quantity distribution of monitoring anchor bolts in each proportion

监测锚杆选取比例还与支护锚杆的数量有一定的关系，支护锚杆数量越多，所需的监测锚杆的数量也应越多，但监测锚杆的比例却逐渐减小(图1)，二者呈反幂函数强相关关系(相关系数R为0.69)或反对数强相关关系(相关系数R为0.61)。可见，采用支护锚杆较多的结构体需要的监测锚杆比例比较少，而中小型结构体加固时所需要的锚杆数量较少，为了获取相应的监测数值，所需要的监测锚杆比例可能较高。因此监测锚杆的比例主要视结构面的复杂程度、支护锚杆数量等因素确定。

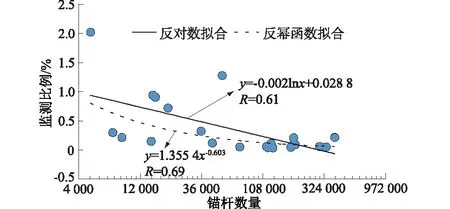
图1 锚杆监测比例与锚杆数量的关系Fig.1 Relationship between bolt monitoring proportion and bolt quantity

2.2 监测锚索比例

10个大型水利水电工程监测锚索数量统计情况见表4和表5。从各监测锚索比例区间发生的案例数看，监测锚索比例≤5%的占比达74.1%，>5%的仅占25.9%,说明大多数情况下，监测锚索的比例不满足规范中>5%的要求。

表4 国内水电工程监测锚索比例统计Table 4 Statistics of monitoring anchor cable proportion in domestic hydropower projects

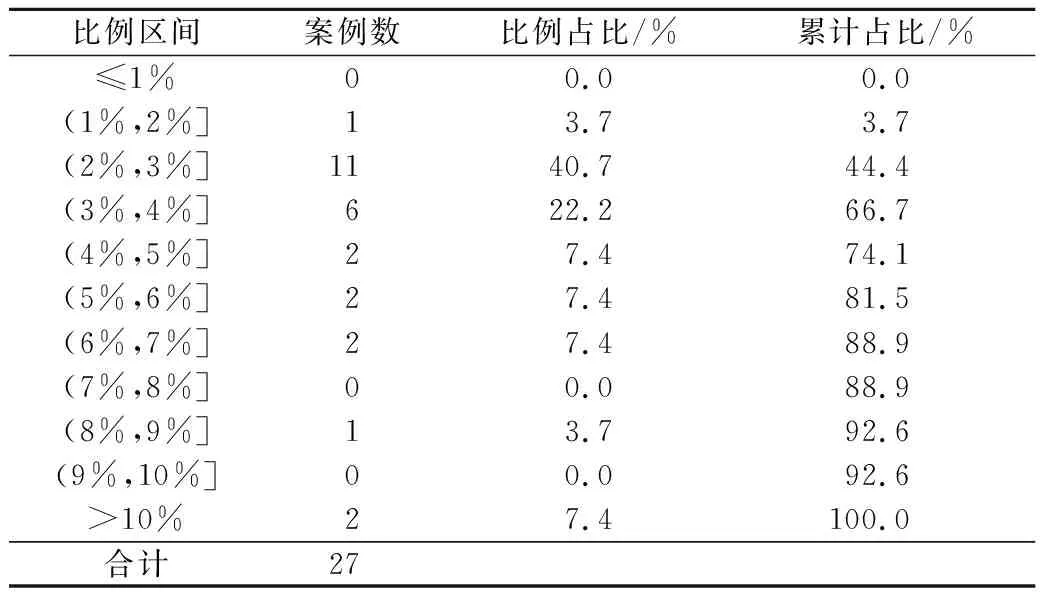
表5 监测锚索比例分布Table 5 Distribution of monitoring anchor cables in each proportion

监测锚索选取比例还与支护锚索的数量有关，支护锚索数量越多，所需监测锚索的数量也越多，但监测锚索的比例却逐渐减小(图2)，二者呈反对数中等程度相关关系(R为0.47)或反幂函数中等程度相关关系(R为0.43)。可见，采用支护锚索较多的结构体需要的监测锚索比例比较少，而中小型结构体加固时所需要的锚索数量较少，为了获取相应的监测数值，所需要的监测锚索比例可以较高。因此监测锚索的比例亦主要视结构面的复杂程度、支护锚索的数量等因素确定。

图2 锚索监测比例与锚索数量的关系Fig.2 Relationship between the monitoring proportion of anchor cables and the number of anchor cables

2.3 锚杆锚索受力特征

工程原型的变形和受力状况无法准确评判，目前主要利用监测仪器评价原型变形及受力的基本规律。本文选取监测仪器较多的白鹤滩水电站左右岸引水发电系统的主厂房锚杆应力监测、锚索受力荷载监测数据(表6)进行监测数据特性分析。

表6 白鹤滩水电站主厂房锚杆及锚索监测仪器特征 统计汇总Table 6 Statistical summary of characteristics of monitoring instruments for anchor bolts and cables of main powerhouse of Baihetan Hydropower Station

从表6数据可以看出，锚杆应力计监测成果的变异系数(标准差/均值)较大，这与实际工程中锚杆监测的规律性较差是一致的；而锚索测力计的变异系数相对较小，工程中往往将其作为最主要的安全评价参数。为进一步分析监测抽样的代表性问题，选取均值200 MPa，标准差100 MPa作为锚杆应力计的代表参数；选取均值2 000 kN，标准差200 kN作为锚索测力计的代表参数。

3 抽样误差研究

为便于进一步的抽样误差分析，忽略工程规模和地质条件等特定条件，将工程问题抽象为纯数学问题进行理论探讨。

3.1 数理统计模型

将在N个支护锚杆(索)中选取n个监测锚杆(索)的过程归纳为一个随机抽样的过程进行数理统计分析，监测仪器比例问题的讨论就变换为用抽样样本来评价总样本所产生的抽样误差问题的分析。

N个锚杆(或锚索)组成一个维度为N的事件总样本X，随机选择其中n个安装监测仪器，得到维度为n的抽样样本x(x1,x2,…,xi,…,xn)。

针对总样本X方差无法确知的情况，用抽样本的均值和均方差评价总样本所产生的误差服从自由度为n-1的t分布[5]，即

(1)

式(1)可归纳为置信度为1-α的概率问题，相应地可得如下概率方程，即

(2)

该方程左侧展开所得置信区间[5]为

将置信区间的一半定义为工程抽样误差δ，则

(3)

针对工程中最常见的不重复抽样问题，式(3)可以修正为式(4)[6]。

(4)

式中σ2为总样本方差。

考虑工程中多为非正态问题，需要作当量正态化处理，将非正态随机变量转换为等效正态随机变量[7-8]。相应地，对总体方差作当量正态化后可得本文所用工程抽样误差δ的计算模型为

式中：f(·)、F(·)分别为非正态概率密度函数与累积分布函数；φ(·)、Φ(·)分别为标准正态概率密度函数与累积分布函数。

3.2 典型案例分析

首先选取代表性的正态分布和均匀分布2种分布模型进行分析，其均值μ=100(为分析方便，此节及下文均值及均方差均不给出单位)，均方差σ=10，显著性水平α=0.01，并由此获得抽样数与相应误差比δ/μ的关系,如图3所示。

图3 正态分布和均匀分布下抽样数和误差比的关系Fig.3 Relation between sample number and error ratio under normal distribution and uniform distribution

从图3可知，当模型参数确定后，抽样误差与所抽取的样本数关系密切，与抽样比例没有直接关系。2种分布模型下，当抽样数<10时，随着抽样数的增加，抽样误差显著下降，即精度显著增加；而当抽样数>50时，抽样误差的下降不明著，即精度增加不明显。抽样数为5～50时各抽样数对应的最大抽样误差比如表7所示。从表7可以看出，抽样数为30～50较为合适。同时结合白鹤滩工程锚杆锚索具体情况(表6)，增加均值μ=200，均方差σ=100，显著性水平α=0.01作为锚杆监测的代表;增加均值μ=2 000，均方差σ=200，显著性水平α=0.01作为锚索监测的代表。相应的计算成果(表8、表9)得到同样的规律。3种算例中，作为锚杆监测算例得到的抽样误差明显大于锚索监测算例，这与工程实际一致。

表7 均值μ=100时不同抽样数对应的最大抽样误差比Table 7 Maximum sampling error ratio corresponding to different sampling numbers when mean number is 100

表8 均值μ=200时不同抽样数对应的最大抽样误差比Table 8 Maximum sampling error ratio corresponding to different sampling numbers when mean number is 200

表9 均值μ=2 000时不同抽样数对应的最大抽样误差比Table 9 Maximum sampling error ratio corresponding to different sampling numbers when mean number is 2 000

3.3 敏感性分析

本文进一步探究δ的敏感性，以正态分布为例，取均值为100，均方差为5～20，显著性水平为0.01～0.10，进行总样本均方差、抽样显著性水平对抽样误差的敏感性分析。不同参数下的抽样数与相应误差关系曲线见图4，相应的抽样数为10时各参数对应最大抽样误差如表10所示。从计算成果看，选取的模型样本均方差和抽样显著性水平要求对抽样误差有一定的影响，均方差越大，相应的抽样误差越大，抽样显著性水平越大，相应的抽样误差比越小，但总体影响不大。可见总体样本的均方差对取样误差影响明显。表7中列出的锚杆监测的变异系数较高，因此其抽样误差也比较大。

图4 正态分布下置信水平和均方差与误差比的关系Fig.4 Relations of error ratio versus confidence coefficient and mean square error under normal distribution

表10 正态分布下不同显著性水平下的最大抽样误差比Table 10 Maximum sampling error ratio corresponding to different significant levels under normal distribution

4 结 论

(1)锚杆锚索监测成果的代表性与所监测点数关系密切，与监测点数的比例无直接关系。

(2)被监测体的不均一性对监测成果误差影响显著。实际工程的锚杆监测中，处于地质结构面上或交叉洞口部位的锚杆监测仪器能监测到较大的应力，而大多数情况下，锚杆监测仪器往往处于完整岩体中因而监测到的应力较小，造成锚杆应力监测成果普通偏小，而且离散性大(变异系数大)。建议进一步开展锚杆监测仪器无黏结化处理等埋设技术的研究，提高锚杆监测对工程安全监控的指导性。

(3)当监测点数<10时，随着监测点数的增加，监测误差显著下降，监测成果的代表性显著增加；当监测点数>50时，监测误差下降不明显；本文建议同批支护结构的监测点数为30～50较为合理。

(4)考虑到当采用大规模锚杆锚索支护时，各区域的地质条件和受力环境存在差异，具体布置时应结合地质条件和工程结构特点综合考虑，不宜统一规定相应的监测比例。