蜂窝菱形组合免充气轮胎性能分析
何宜玖, 祝海林,2, 徐玉凯, 周扬驰
(1.常州大学 机械与轨道交通学院, 江苏 常州 213164; 2.江苏省绿色过程装备重点实验室(常州大学), 江苏 常州 213164)
衡量轮胎性能的指标主要以安全、舒适、耐用为主。现代充气轮胎虽然具有良好的行驶平顺性、减震性及通用性,但其普遍存在磨损、漏气和爆胎等缺陷[1-2]。近年来,免充气轮胎以其优越的性能正在逐渐被熟知,且因其不需要充气,彻底解决了由爆胎而导致的安全隐患。其中仿生蜂窝轮胎结构[3]和菱形轮胎结构[4]的研究都促进了免充气轮胎的发展。2种结构各有其优缺点,菱形结构是鸟巢结构的简化形式,具有抗变形能力强的优点,但结构中应力集中现象明显,会降低轮胎使用寿命;蜂窝结构应力集中现象较前者有很大改善,但其抗变形能力较差,会降低轮胎的承载能力。文章提出将蜂窝和菱形2种结构组合成新型免充气轮胎,并对蜂窝与菱形10种不同数量配比的轮胎结构模型进行有限元性能仿真。
免充气轮胎的胎体结构通常采用聚氨酯弹性材料制成,聚氨酯材料有耐磨、质量轻、抗扎等优点。在保证结构可靠的同时又具有传统轮胎的减震效果[5]。蜂窝菱形组合结构由正六边形和菱形按照数量比例进行组合,边缘作为分隔板。如图1所示,通过改变蜂窝和菱形在整体结构中的配比数量得蜂窝与菱形比例(后文出现比例都如此)分别为1∶1,1∶2,1∶3,1∶4,1∶5,1∶6,1∶7,1∶8,1∶9,1∶10 ,共10组结构,在10 kN的载荷下对轮胎结构静态承载能力、应力分布、接地性能、疲劳寿命以及滚动状态模拟分析。通过研究菱形结构在轮胎整体结构中数量变化对轮胎性能的影响,选出较优配比,对后续结构设计优化提供参考价值。10种结构模型如图2所示。

图1 蜂窝菱形组合轮胎结构单元示意图Fig.1 Schematic diagram of honeycomb rhombichybrid tire structure unit

(a) 1∶1

(b) 1∶2

(c) 1∶3

(d) 1∶4

(e) 1∶5

(f) 1∶6

(g) 1∶7

(h) 1∶8

(i) 1∶9

(j) 1∶10图2 10组蜂窝菱形组合轮胎结构模型Fig.2 Ten structural models of honeycomb rhombic hybrid tire
1 蜂窝菱形组合结构轮胎有限元模型建立
由免充气蜂窝轮胎和菱形轮胎的结构特点,运用三维绘图软件SolidWorks建立相应的模型,再将模型导入到ANSYS Workbench分析软件中,进行分析前处理。主要涵盖材料属性定义、模型尺寸及载荷边界条件确定等。
1.1 材料属性定义
静态仿真中蜂窝菱形组合轮胎主要包括:胎体结构和胎面。另设刚性体作为地面支撑,与胎面接触。蜂窝菱形组合结构胎体选用聚氨酯材料,其具有非常好的耐磨性及弹性,且在工业领域的运用十分广泛。聚氨酯属于弹性材料,故在材料定义时选择Hyperelastic materials中的Moony-Rivlin作为本构模型[6],其应变能函数见式(1)
(1)
式中:W为应变能密度;Cij为Rivlin系数;I1为第一应变不变量;I2为第二应变不变量。
轮胎胎体结构参数:泊松比取0.4,杨氏模量取180 MPa。
1.2 模型尺寸
模型尺寸选用ZL50装载机轮胎尺寸模型,轮胎外径1 615 mm,轮辋直径495.3 mm,轮胎宽度300 mm。菱形结构单元与蜂窝结构单元的边长尺寸100 mm,分隔板宽度10 mm。
1.3 载荷及边界条件
轮胎静载荷状态主要承受车辆自身质量,故在轮辋接触处施加垂直向下的作用力代替实际车辆对轮胎的作用力,在重心处施加轮胎自重的惯性载荷。
静态边界条件设置为:① 运用Sweep网格划分方法[7],模拟轮胎与刚性路面接触问题。选用柔刚面接触单元,在轮胎底部与地面有可能发生接触的范围内采用六面体网格划分,其余部分采用四面体网格划分[8]。轮胎相互作用主要涉及轮胎和轮辋、轮胎与地面。轮胎本身与轮辋固定接触,将其接触侧设为固定接触,轮胎与地面接触设为摩擦接触,摩擦系数设为0.2。② 如图3所示,将轮胎X,Z方向固定,保证轮胎受力时只沿Y轴方向移动。③ 轮辋接触处施加10 kN的垂直载荷,方向由轮胎中心垂直向下。
轮胎滚动状态相较于静态要复杂,既有自重产生的径向下沉又有滚动。采用概念建模方法,将实际中支撑轮胎的汽车悬架机构简化为一根梁,置于轮胎滚动中心,轮胎本身与梁之间设立转动副以达成轮胎滚动效果。
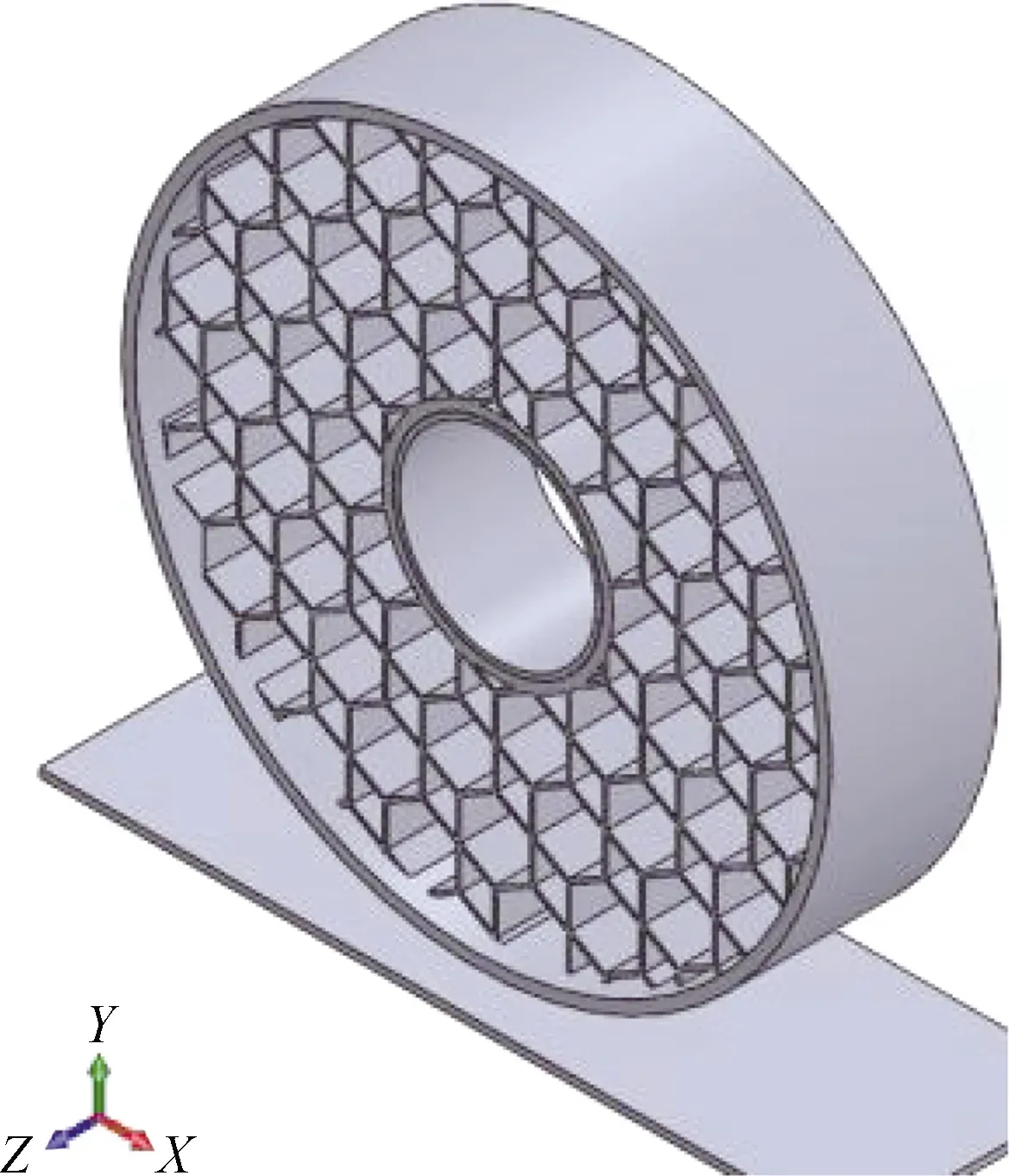
图3 X,Y,Z轴方向示意Fig.3 X,Y,Z axis direction
滚动边界条件设置为:① 接触单元设定同静态相同,轮辋设为固定接触,轮胎表面与地面设为摩擦接触,摩擦系数为0.2。② 汽车悬架机构由于概念建模简化为梁结构,而梁结构本身具有6个自由度,汽车前进时,悬架机构只有Y方向的下沉和X方向的位移,故在远端位移选项中将X,Y,Z轴转动设为0°,Z方向位移固定,X(轮胎前进方向)方向设为Free,Y方向的位移设为静态时轮胎径向下沉量值。
1.4 求解设置
由于此类轮胎与地面接触时涉及3种非线性问题[9],即材料非线性、几何非线性和接触非线性,为避免求解过程不收敛,选用Augmented拉格朗日方程[10]计算轮胎与地面接触问题,使其更易收敛。求解方法选用Interative迭代求解器进行求解。由于材料是弹性材料,且实验施加比较大的力,故将大变形设置设定为on。静态仿真载荷步定义2个阶段,第1阶段施加载荷阶段,步长划分50;第2阶段为保持阶段,步长划分100。滚动仿真分为2个阶段,第1阶段为加载阶段,通过梁的远端位移模拟静态时轮胎受车辆自重的下沉过程;第2阶段为滚动阶段,轮胎向前滚动180°,每滚动30°做一次记录。
2 仿真结果分析
2.1 轮胎静态径向下沉量与接触压力仿真
由约束确定,最大变形量即为径向下沉量,在相同的载荷作用下,下沉量与轮胎的承载能力呈反比,即下沉量越小,轮胎相应的承载能力越强。图4为蜂窝菱形10种比例的组合结构轮胎在10 kN的垂直载荷作用下的径向变形情况。观察径向变形图发现1∶1,1∶3,1∶5,1∶7,1∶10共5种结构径向下沉量变化不大,取其平均值作为参考基线,则1∶2,1∶4,1∶8,1∶9共4种结构低于参考基线,说明其在承受载荷时抗变形能力较好,承载能力相对较高,1∶6结构高于基线,其承载能力较低。随着菱形结构在轮胎整体结构占比的上升,除1∶6结构外,当组合比例为偶数时,轮胎结构径向下沉量较小,抗变形能力较强。

图4 蜂窝菱形组合结构径向下沉量Fig.4 Radial settlement of honeycomb rhombicstructure
在施加载荷相同的情况下,接触面的增大会减小轮胎对地面的接触压强,且轮胎与地面接触面大也会减小震动,提高轮胎舒适性。如图5所示轮胎与地面接触面的长宽(轮胎宽度)比称为轮胎的截面比,长宽比越小抓地力越强。但同时由于接触面积的减小,轮胎的减震舒适度会有所下降。
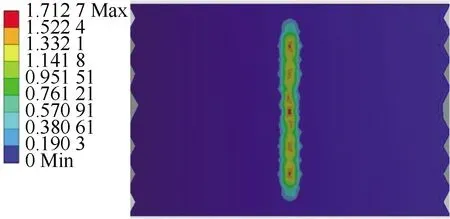
图5 接触面长宽比Fig.5 Aspect ratio of contact surface
轮胎接地性能主要与接触压强和接触面积相关,见式(2)
P=F/S
(2)
式中:P为接触压强;F为接触压力;S为接触面积。
图6为10 kN垂直载荷作用下蜂窝菱形各配比结构的轮胎接触压强图。观察发现1∶3,1∶5,1∶6,1∶8,1∶10共5种结构的接触压强基本一致,取平均值作为参考基线,1∶1,1∶7,1∶9共3种结构的接触压强高于基线,其抓地力相较于其他结构较好,且1∶7结构较与其他最好。1∶2和1∶4结构接触压强低于基线,抓地性不如其他结构,但舒适度有所提升。
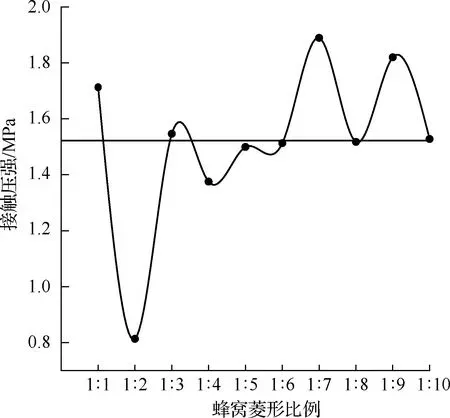
图6 蜂窝菱形组合结构接触压强Fig.6 Contact pressure of honeycomb rhombicstructure
2.2 轮胎静态最大应力与疲劳仿真
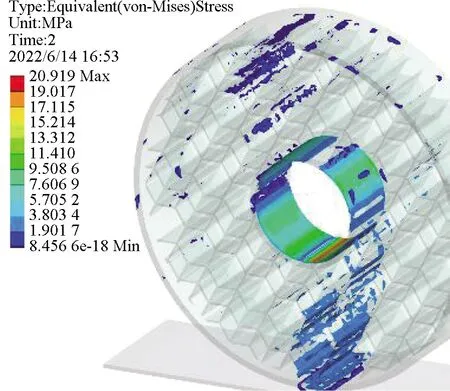
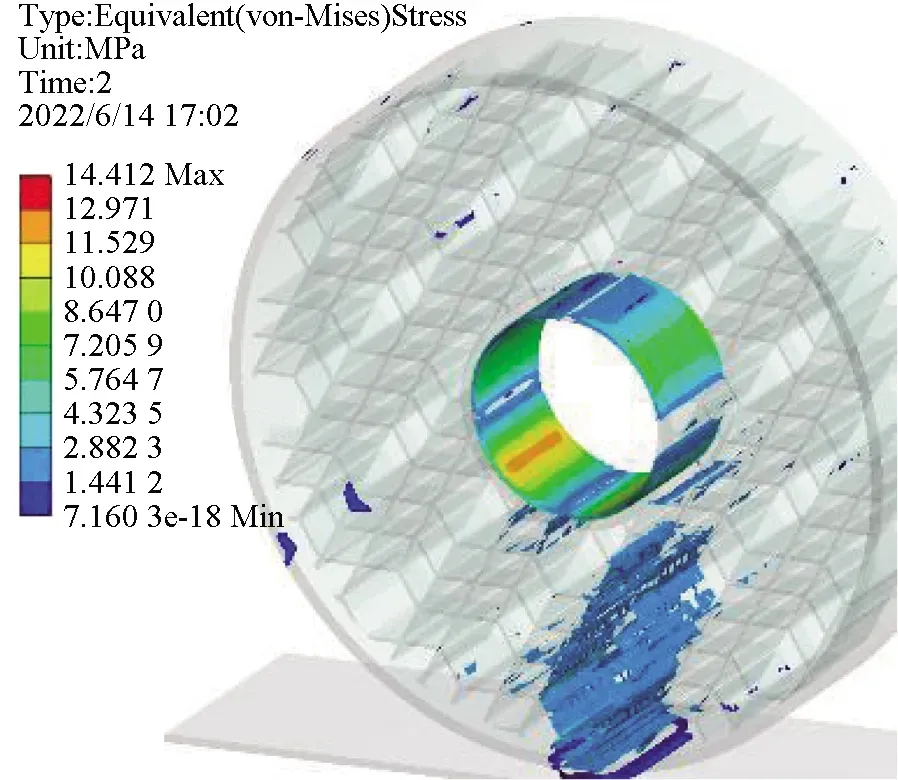
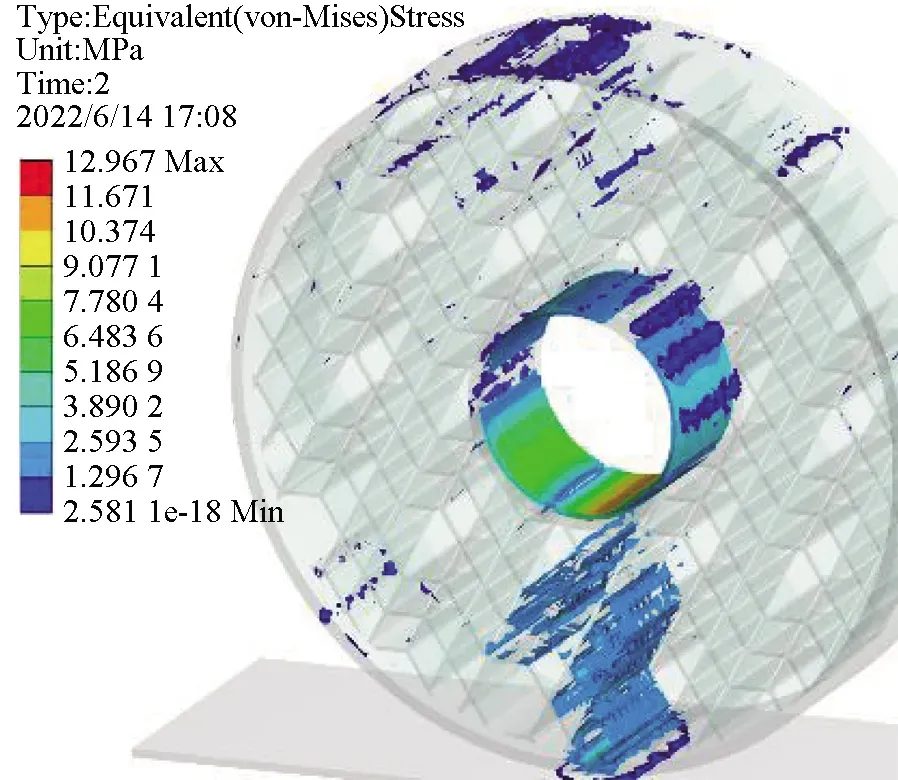
结构中的材料在承受应力的同时,每一次加载都会使材料内部产生一定的损伤,并逐步积累直至破坏,而结构中的应力集中处即最大应力处则是整个结构中的薄弱点,也是最容易发生疲劳破坏的位置,通过输入材料S-N曲线并结合轮胎结构最大应力,可以得到该结构的疲劳寿命。图7和图8为蜂窝菱形各结构在10 kN载荷下的应力分布与最大应力。

(a) 1∶1
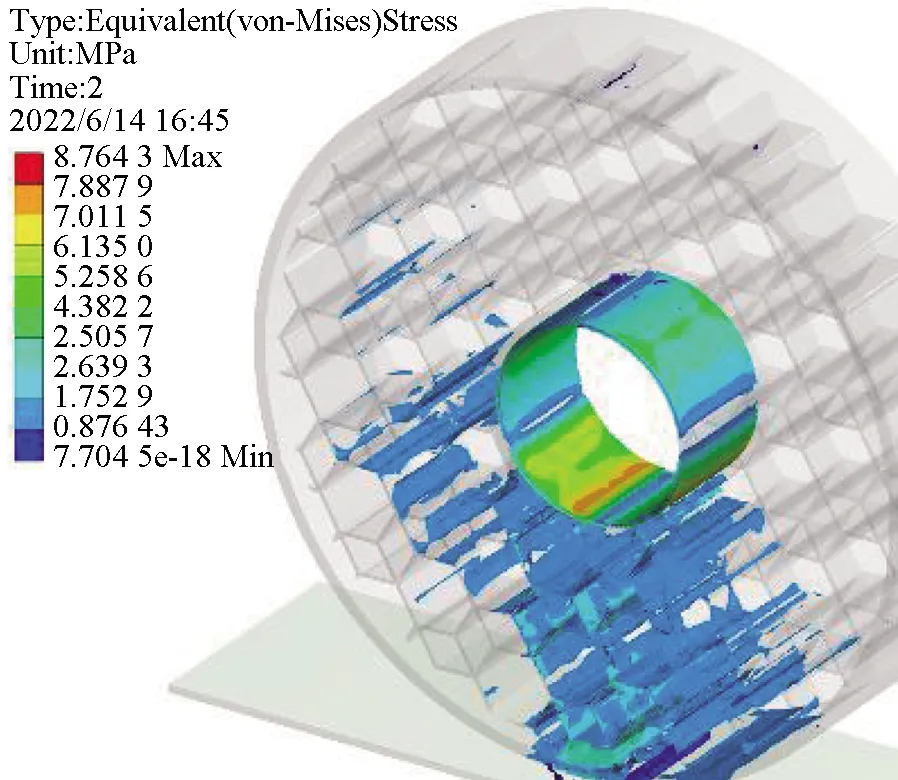
(b) 1∶2

(c) 1∶3
(d) 1∶4

(e) 1∶5

(f) 1∶6
(g) 1∶7

(h) 1∶8
(i) 1∶9
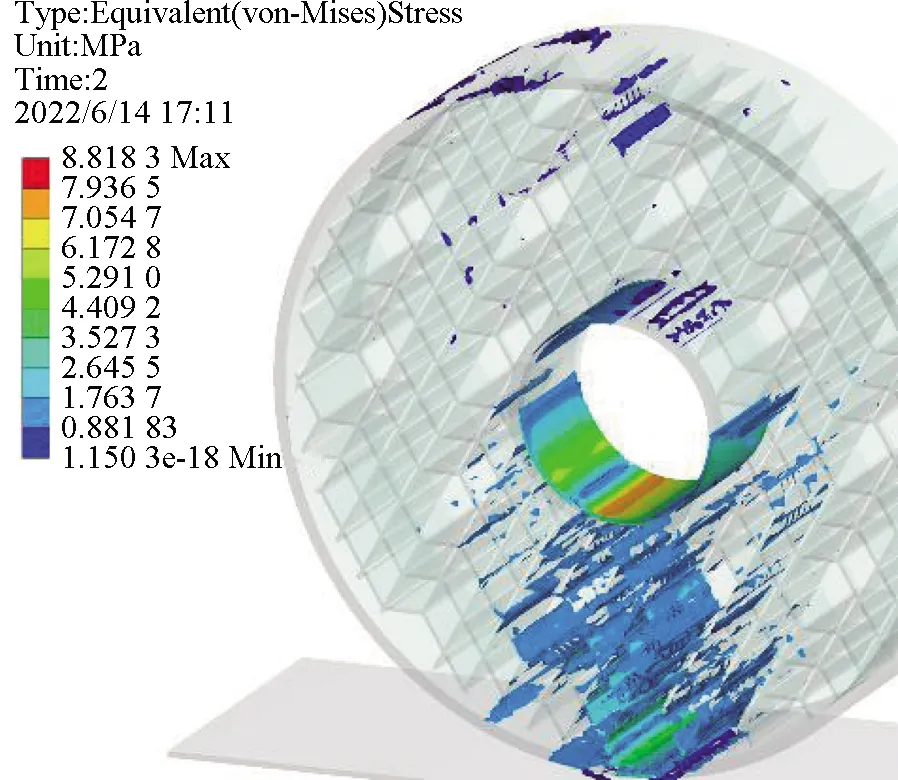
(j) 1∶10图7 蜂窝菱形不同配比的胎体应力分布Fig.7 Stress distribution of honeycomb diamond matrix with different proportions
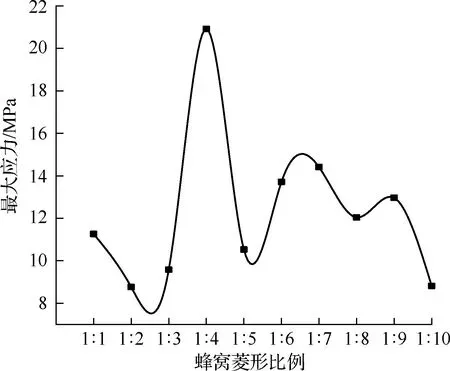
图8 蜂窝菱形不同配比结构最大应力图Fig.8 Maximum stress diagram of honeycomb rhombic structure with different proportions
图9与图10则是以最大应力为基础通过Fatigue tool模块计算得到的该载荷下各结构对应的疲劳寿命分布及疲劳寿命极限。从应力分布角度观察,发现1∶1,1∶2,1∶3,1∶5,1∶8,1∶10结构应力分布超过轮胎面积半数,分布较广,1∶4,1∶6,1∶7,1∶9结构应力分布主要集中在轮胎下半部靠中间范围内,分布较窄。结合最大应力图与疲劳寿命图可知,应力分布广的几种结构由于应力扩散,其最大应力在图中处于低位。由于应力分布广,底部应力传递效果不明显,在图8中其主要疲劳破坏发生在轮胎与地面接触位置,寿命在图9中处于低位。应力分布较窄的几种结构,其最大应力由于扩散面积小传递效果明显在图7中处于高位,但轮胎与地面接触位置的疲劳破坏程度相较于前者更小,其疲劳寿命更高。
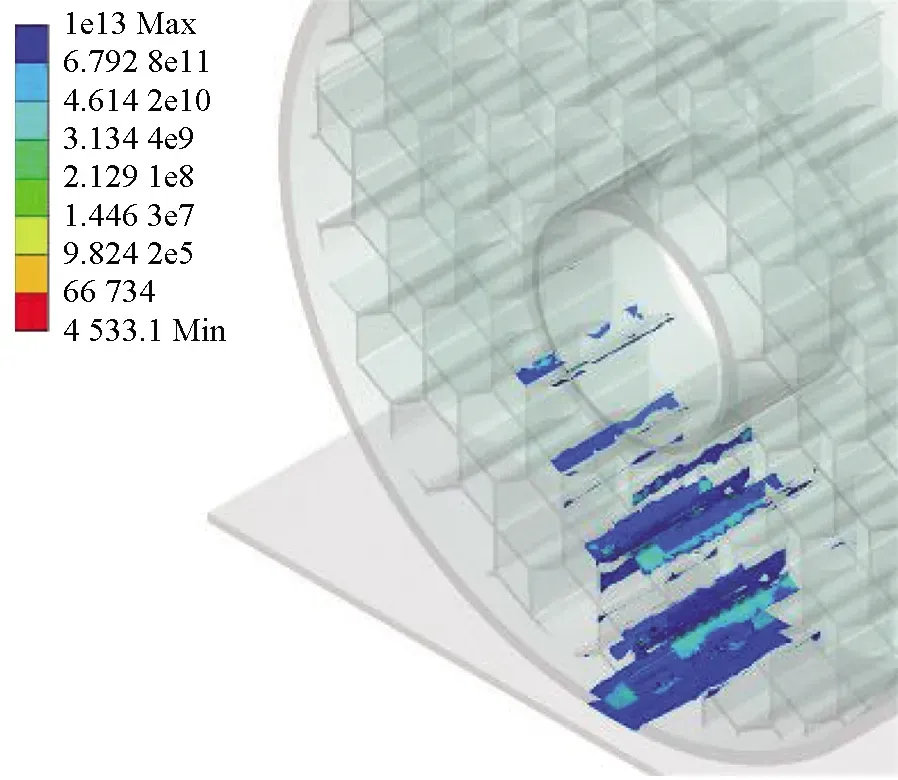
(a) 1∶1
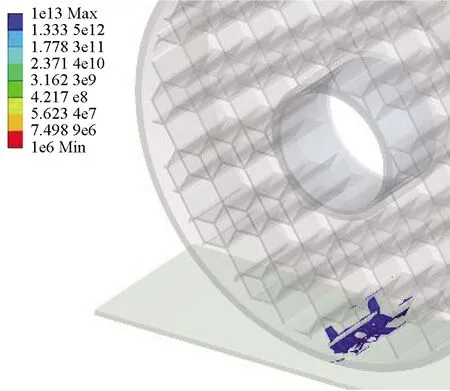
(b) 1∶2
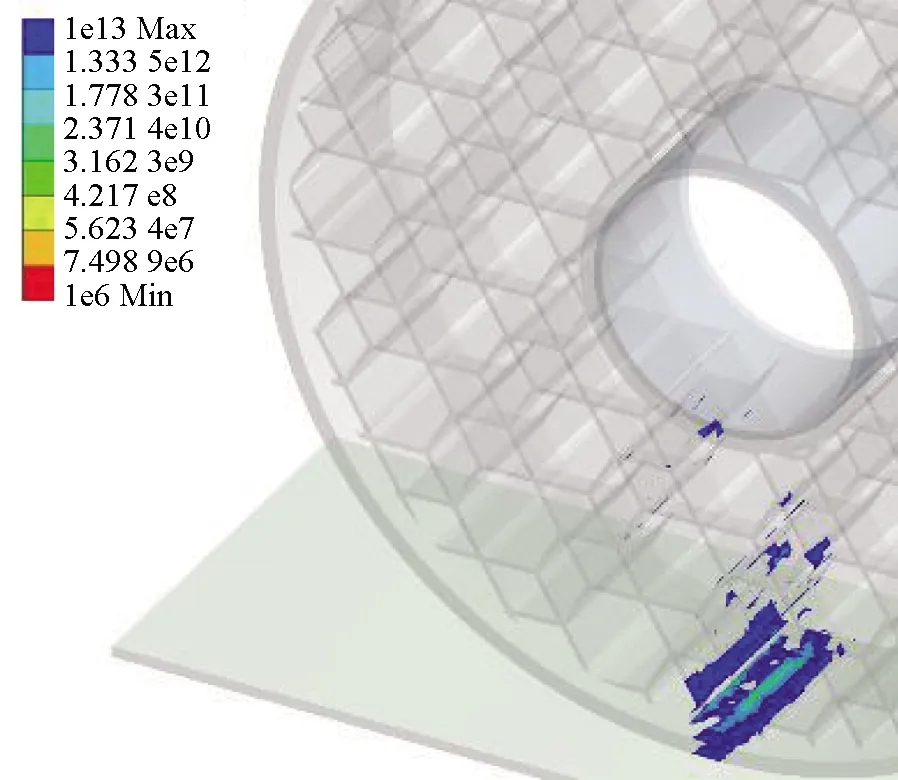
(c) 1∶3

(d) 1∶4

(e) 1∶5

(f) 1∶6
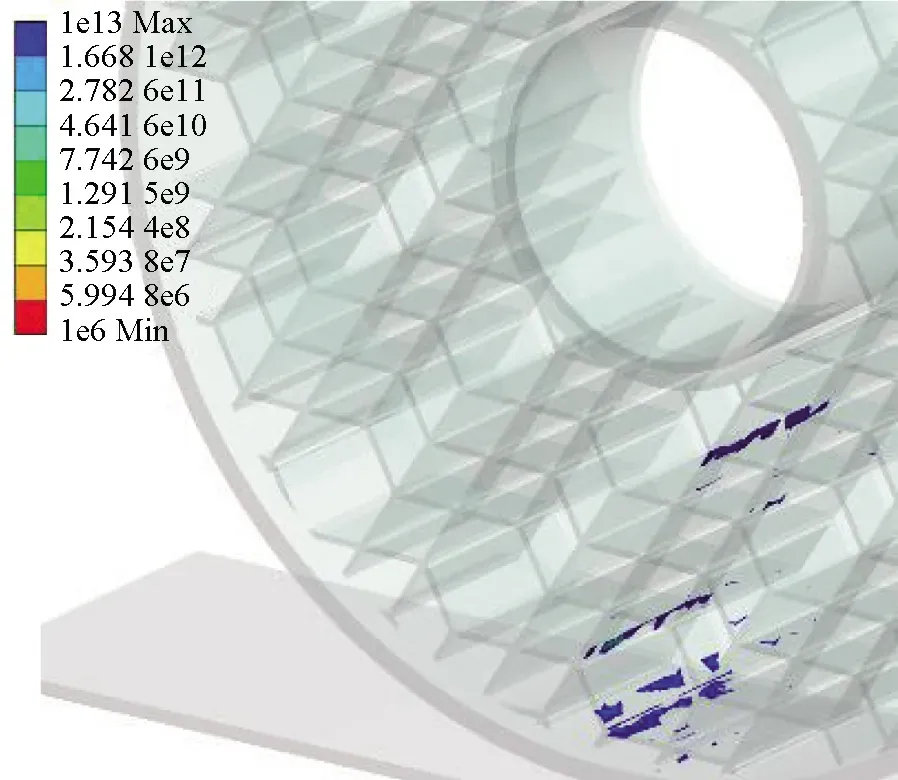
(g) 1∶7
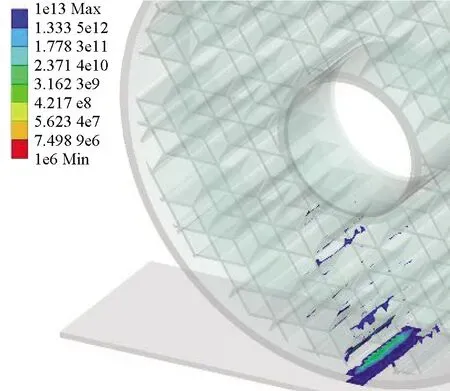
(h) 1∶8
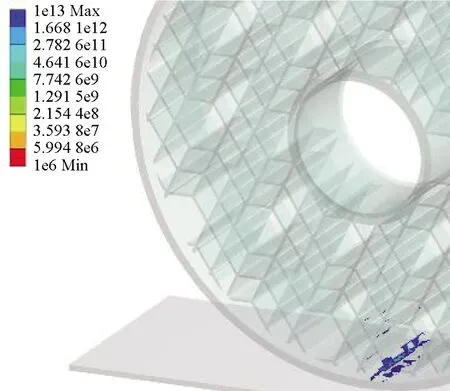
(i) 1∶9
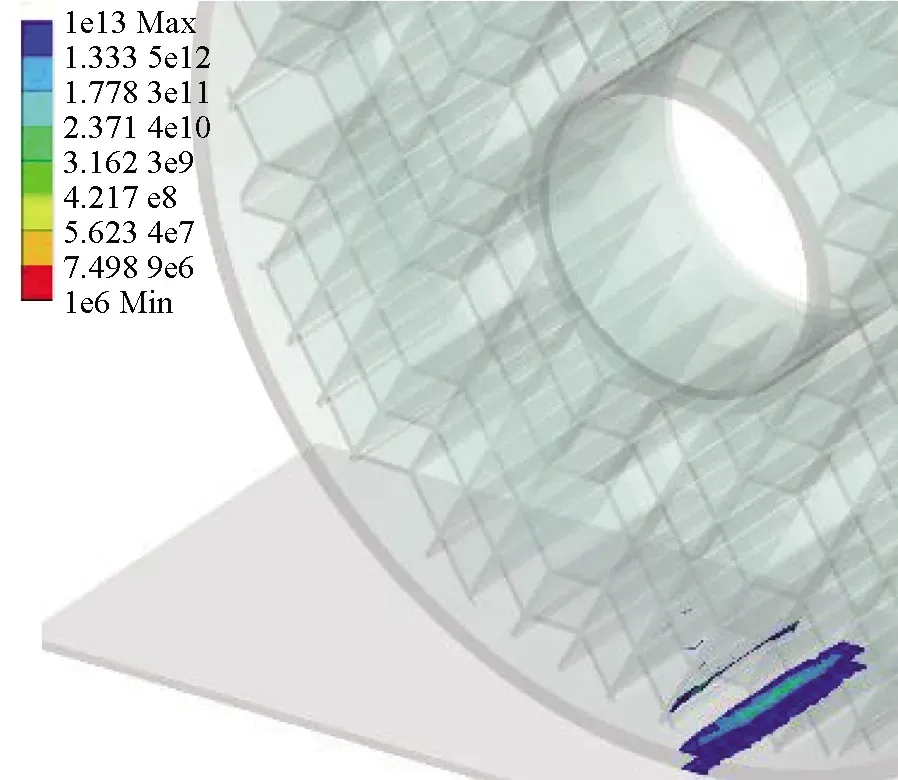
(j) 1∶10图9 蜂窝菱形不同配比结构疲劳寿命分布图Fig.9 Fatigue life distribution of honeycomb diamond structure with different proportion

图10 蜂窝菱形不同配比结构疲劳寿命图Fig.10 Fatigue life diagram of honeycomb rhombic structure with different proportions
2.3 轮胎滚动仿真
轮胎滚动仿真主要用到Ansys中瞬态动力学分析方法,通过分析滚动过程中轮胎结构内部应力以及轮胎与地面接触压强变化趋势,推断出各轮胎结构滚动过程内部应力及接触压强更快趋于平稳。为保证仿真可靠性,先对1∶1结构轮胎进行初步滚动仿真,观察其滚动过程中结构内部应力分布是否符合实际情况。如图11所示为蜂窝菱形1∶1结构轮胎分别在滚动0°,30°,60°,90°时结构内部应力分布。从图11中可看出随着轮胎向前滚动,接近轮胎与地面接触位置的结构应力逐渐增大,远离接触位置的结构应力逐渐减小,符合实际情况。

(a) 滚动0°

(b) 滚动30°

(c) 滚动60°

(d) 滚动90°>图11 轮胎滚动实验Fig.11 Tire rolling test
同理对其余各结构轮胎进行滚动仿真并记录0°,30°,60°,90°,120°,150°,180°时轮胎内部最大应力变化数值。如图12所示,轮胎滚动过程结构内部应力应尽量平稳,从图12中可发现,1∶5与1∶7结构相较于其他结构平稳性要延后,在180°的周期中滚动120°以后才趋于平稳。1∶1,1∶2,1∶4,1∶6,1∶9,1∶10结构在周期内滚动90°后内部应力趋于平稳,1∶3结构则在滚动60°后趋于稳定。1∶8结构相较于其他结构,稳定性最好,在周期内滚动30°后就已趋于稳定。从总体趋势看,随着菱形结构占比的提升,偶数配比的结构应力趋于平稳速度快于奇数配比结构。

图12 滚动应力趋势Fig.12 Rolling stress trend
图13为滚动状态下各结构在各角度下轮胎与地面接触压强趋势,接触压强趋势代表着轮胎与地面在周期内的紧密程度,接触压强的改变表明轮胎与地面接触大小变化,也代表着轮胎在运动过程中上下浮动程度,从侧面也可反映出轮胎舒适度。观察发现,1∶6结构在周期内趋于平稳要滞后于其他结构,在滚动150°以后才趋于平稳。1∶5和1∶7结构在周期内滚动120°后趋于稳定,1∶1,1∶2,1∶4,1∶9结构在周期内滚动90°趋于稳定,1∶3结构在周期内滚动60°后趋于稳定,1∶8和1∶10结构最快趋于稳定,在滚动30°后便趋于稳定。随着菱形结构占比的提升,偶数配比的结构其接触压强的趋于平稳速度快于奇数配比结构。且接触压强的数值偏低,可以提高轮胎舒适性。
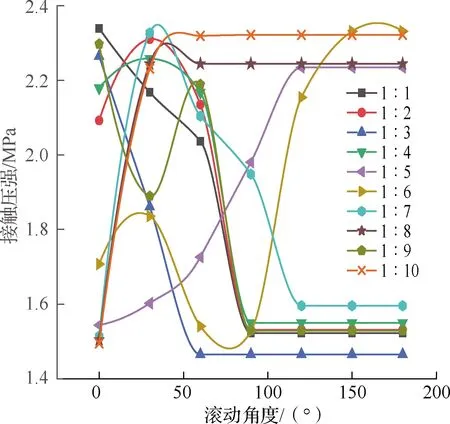
图13 滚动接触压强趋势Fig.13 Rolling contact pressure trend
3 结 论
1) 从承载能力优先角度考虑,将径向下沉量作为主要影响因素,则1∶2,1∶4,1∶8,1∶9结构承载能力较于其他更好。在此基础上,再对其接触压强、滚动应力趋势、滚动接触压强趋势和疲劳寿命作比较,1∶4结构在保证承载能力的基础上拥有更高的疲劳寿命,而1∶8结构则拥有更好的舒适性。
2) 从轮胎舒适性优先角度出发,将接触压强、滚动应力趋势及滚动接触压强趋势作为主要影响因素,1∶2和1∶4结构具有较低的接触压强及相同的滚动平稳趋势,1∶4结构疲劳寿命比1∶2结构更高,可优先选用。此外,1∶8结构虽然接触压强相较于前两者高一些,但其滚动平稳趋势要优于前两者,亦可作为备选结构。
3) 从轮胎疲劳寿命角度出发,将疲劳寿命作为主要参考点,则1∶4,1∶6,1∶7,1∶9结构拥有较高寿命。对比其他几项性能,1∶4结构拥有更好的舒适性,1∶9结构在舒适性方面略逊一筹,但拥有很高的疲劳寿命,二者皆可作为设计备选结构。

