任务执行时间不确定性条件下实时云工作流的可靠调度研究
何 芳 何小东
1(湖南财经工业职业技术学院电子信息系 湖南 衡阳 421002) 2(中南林业科技大学计算机与信息工程学院 湖南 长沙 410004)
0 引 言
云计算是分布式计算的新模式体现,云提供方可以向消费者以即付即用模式按需分发服务,如应用、平台和计算资源等服务[1]。从消费者角度看,云模型是代价有效模型,由于消费者仅需按其实际使用云资源支付代价,且其服务是可扩展的,消费者对于资源的租用是不受限制的。这种特征使云计算在诸多领域得到了广泛应用[2-3]。这类应用通常具有相互关联的计算和数据传输类任务,由于任务间的依赖约束,任务间的大量空闲时槽将被虚拟机资源所浪费,导致虚拟机资源整体利用率不高[4]。此外,云平台较低的资源利用率也会浪费大量代价,资源利用率的提升也是代价有效的整体调度手段。
有效的工作流任务调度算法是解决以上云平台问题的有效方法。然而,已有方法基本都是以准确的任务执行时间和任务间的通信时间信息为前提条件。而在实际的云环境中,任务执行时间通常无法进行准确可靠估计,仅在任务完成后,任务的准确执行时间值才是可用的,主要原因在于:(1) 工作流任务通常在不同输入下包含条件式指令,即特定应用中的任务通常包含多种选择和条件语句,其程序分支和循环不尽相同,使得任务的计算时间在不同的数据输入下体现出极大的不同;(2) 云平台中虚拟机的性能随时间发生变化。以Xen和VMware等虚拟机技术为例,其多个虚拟机可以同步地分享相同的物理主机硬件资源,如CPU、I/O和网络资源等。这种资源分享模式可能导致虚拟机的性能遭遇到虚拟机间资源干扰的影响而产生诸多的不确定性[5]。
由于云平台的动态性和不确定性,如可变的任务执行时间、可变的虚拟机性能以及动态的工作流的到达,均可能导致预定的调度方案无法有效地运行于实际环境中。已有的工作流调度算法均忽略了这些动态不确定性因素,为了解决这种不确定性,提高虚拟机资源利用率和降低执行代价,本文将设计一种基于不确定性环境的云工作流调度算法,并对其有效性和可行性做出实验验证。
1 相关研究
已有的工作流调度算法可以划分为表调度、聚类调度和元启发式调度。文献[6]设计了一种基于表调度的工作流调度算法MO-HEFT,可以均衡调度跨度与能耗。文献[7]设计了两阶段调度方案,先生成确保执行跨度最小的调度方案,然后进一步最小化资源浪费率得到更优的调度方案。文献[8]提出了一种基于局部关键路径PCP的工作流调度算法,在确保工作流截止时间约束的同时最小化工作流执行代价。文献[9]在以上工作的基础上,设计了IC-PCP工作流调度算法。另外,元启发式方法也是求解工作流调度问题的有效方法。文献[10]设计了基于遗传算法的工作流调度算法,利用赋予任务优先级的方式,启发式地将每个任务映射至处理器上执行。文献[11]提出了进化多目标优化算法求解云工作流调度问题。然而,以上方法均是针对单一工作流的调度环境,并且忽略了云平台中任务执行时间的不确定性和工作流应用的动态特征。
针对随机计算环境下的工作流调度问题,文献[12]通过任务复制的方法减轻工作流调度时资源性能变化对于工作流截止时间的影响。文献[13]设计了基于随机启发式方法的工作流调度算法最小化工作流执行跨度。文献[14]基于蒙特卡罗方法处理工作流任务执行时间的不确定性。文献[15]则侧重于虚拟机的性能变化,设计了基于粒子群优化的工作流调度算法,可以在确保截止时间条件的同时最小化全局工作流执行代价。然而,以上算法也是相对于单一工作流调度环境设计的调度算法,不适用于动态的云计算平台,也无法有效处理多工作流的提交环境。
2 问题描述
2.1 云虚拟机模型
云计算可提供多种类型的虚拟机服务,定义为:V={v1,v2,…,vm},每种虚拟机类型vi均具有特定性能配置和使用代价,i∈{1,2,…,m}。不同虚拟机类型配置拥有不同的CPU性能、内存、存储和网络带宽等性能。令P(vi)代表虚拟机vi的使用代价,以单位时间收费。不满单位时间的虚拟机租用依然按一个时间单位收费。令VMk,vi代表虚拟机类型vi的第k个虚拟机,令WBkh代表虚拟机VMk,vi与虚拟机VMh,vj间的网络带宽,并忽略网络通信之间可能产生的网络拥塞,以简化任务调度模型。
2.2 工作流任务模型
云平台下的工作流应用可被用户连续提交执行需求,将这类工作流应用定义为:W={w1,w2,…,wm}。某一特定工作流应用wi∈W可定义为wi={ATi,Di,Gi},ATi为工作流的到达时间,Di为工作流完成的截止时间,Gi为工作流的结构模型。工作流wi的结构Gi可建立为无向无环图DAG模型,表示为Gi=(Ti,Ei),Ti={t1,i,t2,i,…,ti,|Ti|}代表有向图中的顶点集合,表示任务节点,ti,j代表工作流wi中的任务j,Ei⊆Ti×Ti代表任务节点间的有向边集合。有向边eipj∈Ei若存在于有向图中,即表明任务tip与任务tij之间存在依赖约束关系,而任务tip可称为任务tij的直接后继任务。有向边eipj的权重值w(eipj)代表任务tip与任务tij之间传输数据量。由于有向图中的某个任务可能存在多个前驱任务或后继任务,令pred(tij)表示任务tij的前驱任务集合,succ(tij)表示任务tij的后继任务集合。对于不确定性环境而言,由于云虚拟机资源性能的变化以及系统负载的不确定性,任务的准确执行时间是无法提前预知的,因此任务执行时间可理解为一个随机变量,并具有独立性,服从正态分布。
2.3 调度模型
具有不确定性的云平台中的工作流调度模型如图1所示。平台由用户层、调度层和资源层三个部分构成。云调度平台中,用户负责向资源提供方发送工作流应用执行需求,调度层负责依据制定的调度策略,并根据确定的目标函数和资源性能状况,生成每个工作流任务与虚拟机资源间的映射关系,资源层由大规模的异构虚拟机资源构成,而这些虚拟机的性能可以动态的缩放以满足不同需求的用户任务。

图1 调度模型
调度层主要由工作流任务集模块、调度分析模块、资源调节控制模块及任务分配控制模块组成。工作流任务集模块负责接收等待的工作流任务,调度分析模块负责生成计算资源的扩展性能和等待任务与虚拟机资源间的映射关系,计算资源的扩展调节包括何时添加或删除不同类型虚拟机资源的数量,并由资源调节控制模块对其执行。任务分配控制模块负责动态地根据任务与虚拟机间的映射关系将等待的工作流任务分配至对应的虚拟机上执行。该调度模型的主要特征是多数的等待任务均会在工作流任务集模块中处于等待状态,而不是直接处于虚拟机的等待队列中,而仅有一个就绪任务被直接映射至虚拟机上,即每台虚拟机仅允许一个任务等待。
2.4 最优化模型
定义变量xi,j,k用于表示任务ti,j与虚拟机VMk,vh间的映射关系,并满足以下条件:
(1)
令r(ti,j)表示任务ti,j映射的虚拟机的序号。由于工作流任务的执行时间是随机变量,利用其α分位数表示执行时间的近似值。令ETα,ijk表示任务tij在虚拟机VMk,vh上执行时间的α分位数。令PSTij,k表示任务tij在虚拟机VMk,vh上的估计开始时间,PFTij,k表示任务tij在虚拟机VMk,vh上的估计完成时间。估计开始时间计算方式如下:
(2)
式中:PFTlh,k表示虚拟机VMk,vh上最后一个任务tlh的估计完成时间;r(tip)表示任务tip调度的虚拟机的序号;TTipj表示任务间的有向边eipj上的数据传输时间。
工作流wi的所有任务调度后,其估计完成时间可定义为:
(3)
任务完成后,其实际开始时间、执行时间和完成时间将是准确可知的。令RSTijk、RETijk和RFTijk分别表示任务tij在虚拟机VMk,vh上的实际开始时间、实际执行时间和实际完成时间。因此,工作流wi的实际完成时间可定义为:
(4)
不确定性的调度环境中,工作流wi的实际完成时间RFTi决定了任务的执行时间需求是否可以确保。因此,以下约束条件需要务必满足:
(5)
由于工作流应用中任务间存在顺序约束,一个任务仅能在其所有前驱任务完成后才能被执行,因此需要满足以下约束:
RSTijk≥RFTip,r(tip)+TTipj∀eipj∈Ei
(6)
结合以上的两个约束条件,工作流集合W调度的第一个目标是最小化总体执行代价,即:
(7)
式中:|VM|为执行工作流集合W的虚拟机总量;Wk为虚拟机VMk,vh的工作时间。
资源利用率最大化是调度算法的第二个目标,可定义为:
(8)
式中:WTk和TTk分别为工作流集合W执行时虚拟机VMk,vh的工作时间和总活跃时间(包括工作时间和空闲时间)。
在不确定性环境下,另一个需要优化的目标是最小化方差代价函数,定义为工作流的估计完成时间与实际完成时间绝对差的权重之和的均值,表示为:
(9)
式中:τi为估计完成时间与实际完成时间的时间差的边界代价。
3 算法设计
由于工作流任务的执行指令与虚拟机性能的变化,任务的准确执行时间在调度前通常无法准确估算。因此,工作流任务的执行时间和完成时间是具有不确定性的。调度任务时,如果执行任务的预留时间过短,任务的实际完成时间将大于其期望完成时间,进而会导致其他任务执行的延迟,并违背任务执行的截止时间约束。因此,本文设计了一种主动式调度策略用于建立工作流的底线调度方案,该方案利用了工作流的最差执行时间。本文中,当α远大于0.5或小于1时,算法将任务执行时间的α分位数考虑为最差执行时间。但是,工作流任务在多数情况下的执行时间会小于最差执行时间。因此主动式工作流调度策略会浪费大量资源性能。为了处理这种影响,任务执行期间,需要设计一种基于响应式的工作流调度策略,能够动态调度等待任务以充分利用剩余资源性能。
将以上主动式调度和响应式调度划分为两类事件的发生:一是新的工作流到达时进行主动式调度,二是当虚拟机完成一个任务时进行响应式调度。
3.1 基于任务执行时间不确定性的任务分级
工作流任务集合中的所有任务依据其估计最迟开始时间PLSTij进行分级,任务tij的估计最迟开始时间PLSTij定义为任务开始执行后,工作流wi的估计完成时间PFTi将大于其截止时间Di的最迟时间,定义为:
(10)
式中:succ(tij)为任务tij的直接后继任务集合;METα,ij为任务tij的执行时间的α分位数的最小值。
则任务tij的估计最迟完成时间PLFTij可计算为:
PLFTij=PLSTij+METα,ij
(11)
3.2 调度算法设计
一个任务视为就绪任务,当其不存在任一前驱任务,即pred(tij)=null,或其所有前驱任务已被映射至虚拟机上,且至少一个前驱任务已经完成。传统的工作流调度方法中,一旦新的工作流到达,其所有任务被直接调度至虚拟机的本地队列中。本文的调度策略不同,将多数等待任务放入工作流任务集合中,仅有一个就绪任务被调度和分配至虚拟机。在整个云平台的实际执行过程中,工作流任务集合中的等待任务的新的映射方案将连续生成。算法1为执行当新的工作流到达时的主动式工作流调度策略。
算法1新工作流到达时的主动式工作流调度策略
1.taskSet←null
2.foreach new workflowwiarrivesdo
3. 通过式(11)和式(12)计算PLSTijandPLFTijfor eachtijinwi
4.readyTasks←get all the ready tasks in workflowwi
5. sortreadyTasksby tasks’ ranks in an increasing order
6.foreach ready tasktijinreadyTasksdo
7. scheduletijby Algorithm 3
8.endfor
9. add all the non-ready tasks inwiinto settaskSet
10.endfor
步骤1首先将工作流任务集合置为空集。当新的工作流wi到达时,算法1通过步骤3计算工作流中每个任务的估计最迟开始时间和估计最迟完成时间。步骤4将工作流中的所有就绪任务放入就绪任务集合中,并在步骤5中根据任务的分级值的递增排序对就绪任务进行排列。最后,在步骤6-步骤8中,通过调用算法3将这些就绪任务调度至虚拟机上执行。步骤9则将新工作流中的所有的非就绪任务添加至工作流任务集合中。
由于任务在一个虚拟机上的完成时间是随机的,将一台虚拟机上的一个任务的完成事件视为一个突发事件。当突发事件发生时,如果虚拟机上存在等待任务,则第一个等待任务立即开始执行(其所有前驱任务已经完成)。此外,当一个任务完成时,其后继任务变为就绪任务,此时将触发算法1对就绪任务进行主动式调度。算法2执行当虚拟机完成一个任务时的响应式调度。
算法2虚拟机完成一个任务时的响应式调度
1.ifthere exist waiting tasks onVMVMk,vithen
2. start to execute the first waiting task onVMVMk,vi
3.endif
4.readyTasks←null
5.fortis∈succ(tij)do
6.iftasktisis readythen
7. readyTasks←(readyTasks+tis)
8.endif
9.endfor
10.taskSet←(taskSet-readyTasks)
11. sortreadyTasksby their ranksPLSTijin an increasing order
12.foreach readytasktij∈readyTasksdo
13. schedule tasktijby Algorithm 3
14.endfor
在步骤1~步骤3中,当虚拟机VMk,vi完成其执行的任务后,如果其等待任务队列wtkk为非空,则立即开始执行该队列中第一个等待任务。然后,选择处于就绪状态的任务tij的后继任务,即步骤4-步骤9。具体地,步骤4首先将就绪任务队列置为空,然后在步骤5-步骤9中遍历当前就绪任务tij的所有后继任务,在步骤6中判断该后继任务是否为就绪状态,若为就绪状态,则更新当前就绪任务队列readyTasks。步骤10将以上就绪任务从工作流任务集合taskSet中移除。步骤11中,算法根据估计最迟开始时间PLSTij对就绪任务进行递增排序并更新就绪任务队列。根据式(11)定义可知,按照最迟开始时间递增排序后按序调度就绪队列中的任务,可以确保工作流任务间的执行顺序约束。最后,对于所有处于就绪任务集合中的任务,通过算法3将就绪任务调度至虚拟机上执行,即步骤12-步骤14。
任务tij在虚拟机VMk,vi上的估计代价为:
Pcij,k=P(VMk,vi)×(PFTij,k-PRTk)
(12)
式中:PRTk代表虚拟机VMk,vi对于任务tij可用的估计时间。算法3用于对处于就绪状态的任务进行调度。
算法3调度处于就绪状态的任务
1.minCost←∞,targetVM←null
2.foreachVMVMk,vithe systemdo
3.通过式(3)和式(13)计算PFTij,kandPcij,kfor tasktijonVMVMk,vi
4.ifPFTij,k≤PLFTijandPcij,k 5.targetVM←VMk,vi,minCost←Pcij,k 6.endif 7.endfor 8.iftargetVM!=nullthen 9.schedule tasktijto thetargetVM 10.else 11.lease a newVMVMk,viwith the minimalPcij,kwhile satisfyingPFTij,k≤PLFTij 12.schedule tasktijtoVMVMk,viafter it has been initiated 13.endif 步骤1对算法得到的最小执行代价和调度目标虚拟机进行置空初始化。算法利用了两种方式将一个就绪任务调度至虚拟机上。方法一对于能够在其估计最迟完成时间PLFTij以内且以最小的估计代价Pcij,k完成任务的初始化的虚拟机(步骤4-步骤6),将选择为完成该就绪任务的虚拟机,即步骤2-步骤7所示。如果该方法不能为就绪任务找到合适的虚拟机,方法二将租用一个生成最小估计代价Pcij,k,且在其估计最迟完成时间PLFTij以内完成该任务的新的虚拟机进行任务调度,即步骤10-步骤13。 利用CloudSim云计算仿真平台实现云平台中工作流任务调度问题的仿真。为云平台配置六种不同类型的虚拟机,每种类型的虚拟机配置数量不受限制。表1给出以上虚拟机的具体配置,具体包括虚拟机类型名称、使用代价、CPU的内核数量及扩展因子,该配置参考了亚马逊的弹性计算云EC2的配置参数,具备很好的代表性。此外,虚拟机的租用时间单位为一小时,虚拟机之间的网络带宽设置为1 Gbit/s。 表1 虚拟机配置参数 利用四种现实工作流模型进行算法的仿真测试,包括Montage工作流、SIPHT工作流、CyberShake工作流和LIGO工作流,这些工作流模块集合中包括多种描述元素,具体参考文献[16]。设置三种不同规模的工作流任务模型,30个任务组成小规模工作流执行模型,50个任务组成中等规模工作流执行模型,100个任务组成大规模工作流执行模型。另外,为了实现云平台中工作流执行的动态特征,工作流模块在固定的时间间隔内进行随机选取,并发送至调度器上。两个连续工作流的时间间隔为一个变量,令其服务1/λ=100 s的泊松分布。 由于虚拟机类型不尽相同,导致任务的基准执行时间不同类型的虚拟机上也是不相同的。利用扩展因子f描述以上不确定性特征。任务tij在不同虚拟机类型上的基准执行时间计算为: BETij,k=BETij×f (13) 式中:k为虚拟机的类型序号,对应于扩展因子f的虚拟机。 将每个任务的执行时间建立为正态分布,即ETij,k=N(μ,δ),任务基准执行时间均值为μ,相对任务执行时间标准方差为δ: μ=BETij,k δ=BETij,k×var (14) 式中:var为任务执行时间的变化。 实验中,任务的实现执行时间为: RETij,k=r_N(BETij,k,(BETij,k×var)2) (15) 式中:r_N(μ,δ2)表示随机数生成器,用于生成均值为BETij,k和标准方差为(BETij,k×var)的正态分布值。 为了给每个工作流分配截止时间,定义最快调度方案为将每个工作流任务调度至最快的虚拟机(即表1中的M2.xlarge虚拟机)上执行得到的调度结果,参数MF定义为一个工作流的最快调度方案下得到的执行跨度。令u表示截止时间因子,将工作流的截止时间设置为: Di=ATi+u×MF (16) 选择IC-PCP工作流调度算法[9]和WSTR工作流调度算法作为对比算法[12],保留两种算法的调度思路,并在仿真实验环境中将其扩展为可调度多工作流的调度模型。 首先分析不确定性的任务执行时间对性能的影响,改变任务执行时间变化参数var的值,将其设置在0.1至0.5之间,并以步长0.1进行递增。图2为该参数对于工作流执行代价、资源利用率和方差代价的影响。图2(a)显示,随机该参数的增加,工作流执行代价在不同算法间以不同的递增速率增加,两种对比算法的增加趋势比本文算法更加明显。这是由于两种对比算法均未采用任何响应式调度策略控制任务执行时间的不确定性和云平台中资源性能的动态性,而仅是以基准调度方案进行任务执行。本文算法相较两种对比算法IC-PCP和WSTR算法分别降低了65%和48%左右的执行代价,这表明本文算法可以降低云提供方的代价,且不受任务时间可变和不确定性的影响。图2(b)表明本文算法得到的资源利用率始终处于较高的水平,远远高于另外两种对比算法。原因在于:(1) 当等待任务处于就绪时,本文算法动态将就绪任务调度至虚拟机上,使得每个虚拟机上的空闲时槽被大大压缩。(2) 两种对比算法中执行时间变量的增加导致任务的估计完成时间与实际完成时间之差变得更大,这大大地浪费了调度时间,同时导致了更低的虚拟机资源利用率。图2(c)表明,随着执行时间参数的增加,三种算法的方差代价均有所增加,这是由于该参数的增加使得估计完成时间和实际完成时间之差变大。此外,本文算法的方差代价要低于对比算法,由于它们并没有控制等待任务的不确定性。 (a) 任务执行时间变化对执行代价的影响 (b) 任务执行时间变化对资源利用率的影响 (c) 任务执行时间变化对方差代价的影响图2 任务执行时间变化对性能的影响 图3分析了截止时间因子的设置对于算法性能的影响,不同的截止时间因子可以生成不同大小的工作流截止时间。由图3(a)可以看到,三种算法的执行代价会随着截止时间因子的增加(即工作流的截止时间变得更加宽松)而轻微下降,这表明截止时间延长时,可以使工作流在时间约束内更迟完成。相应地,更多的工作流中的并行任务(任务间不具有执行顺序依赖关系)可以执行在相同的虚拟机上,使得更少量的虚拟机被利用,资源利用率得以提高。此外,本文算法的执行代价对两种对比算法的代价平均低44%和76%,该结果表明融合了主动式调度策略和响应式调度策略的本文算法在降低执行代价方面是有效可行的。由图3(b)可以看到,当截止时间因增加时,三种算法的资源利用率会相应增加,这是由于工作流执行的截止时间变长时,其执行跨度在不违背截止时间约束的同时也会变长,进而使得虚拟机资源的空闲时槽大大压缩和减少。本文算法得到的资源利用率平均来说要分别高于对比算法30%和40%,本文算法得到极高的资源利用率是由于算法仅在任务变为就绪状态时就直接动态地调度至虚拟机上执行,使得虚拟机的空闲时槽被大大减少。图3(c)的结果表明,随着截止时间因子的增加,本文算法和WSTR算法的方差代价轻微增加,而IC-PCP算法则基本保持不变。此外,本文算法的方差代价平均来说低于两种对比算法,原因在于两种对比算法在一旦有新的工作流到达时就立即调度其所有任务至虚拟机上,导致任务执行时间不确定性对性能造成了较大的影响。图3结果表明本文算法在处理调度不确定性时具有很好的控制功能。 (a) 截止时间因子对执行代价的影响 (b) 截止时间因子对资源利用率的影响 (c) 截止时间因子对方差代价的影响图3 截止时间因子对性能的影响 实验最后观察执行工作流的规模对于系统性能的影响,如图4所示。由图4(a)可见,三种算法的总体执行代价会随着工作流执行数量的增加而得到增进。很明显,执行的工作流数量越多,越需要更多的虚拟机工作时间,导致了更高的执行代价。而本文算法的执行代价依然比两种对比算法分别低54%和71%。图4(b)表明,工作流执行数量增加时,三种算法的资源利用率基本会稳定在77%、50%和45%左右。该结果表明工作流执行数量的增加对于云平台下的资源利用率的影响比较有限。图4(c)的结果表明,三种算法的方差代价分别为0.055、0.15和0.3,这表明工作流执行数量的增加对基准调度的影响甚少。本文算法得到较低的方差代价是由于能够通过主动式和响应式调度策略将任务执行时间不确定性降低至最小,从而得到与实际调度情形更加接近的工作流调度解。 (a) 执行工作流的数量对执行代价的影响 (b) 执行工作流的数量对资源利用率的影响 (c) 执行工作流的数量对方差代价的影响图4 执行工作流的数量对性能的影响 为了改善云平台下多工作流的执行代价和资源利用率,提出一种不确定性感知的工作流可靠调度算法。该算法利用主动式和响应式的调度策略,可以实时触发新工作流的调度请求和响应虚拟机完成任务后的任务调度请求,并满足多工作流的执行环境。在现实工作流模型的测试表明新的工作流调度算法可以在确保满足截止时间约束的同时,极大降低工作流执行代价和提高虚拟机资源利用率,并将不确定性影响降至最低。4 性能评估
4.1 实验搭建和参数配置
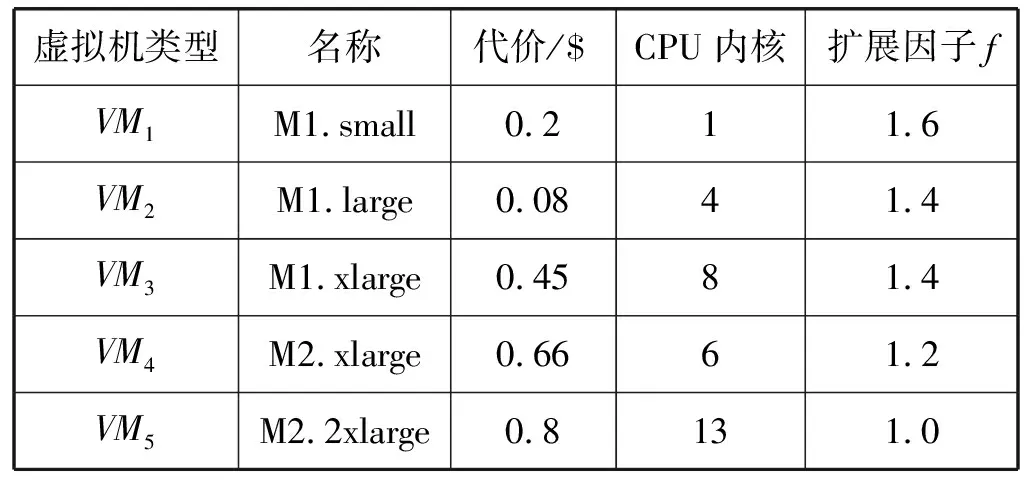
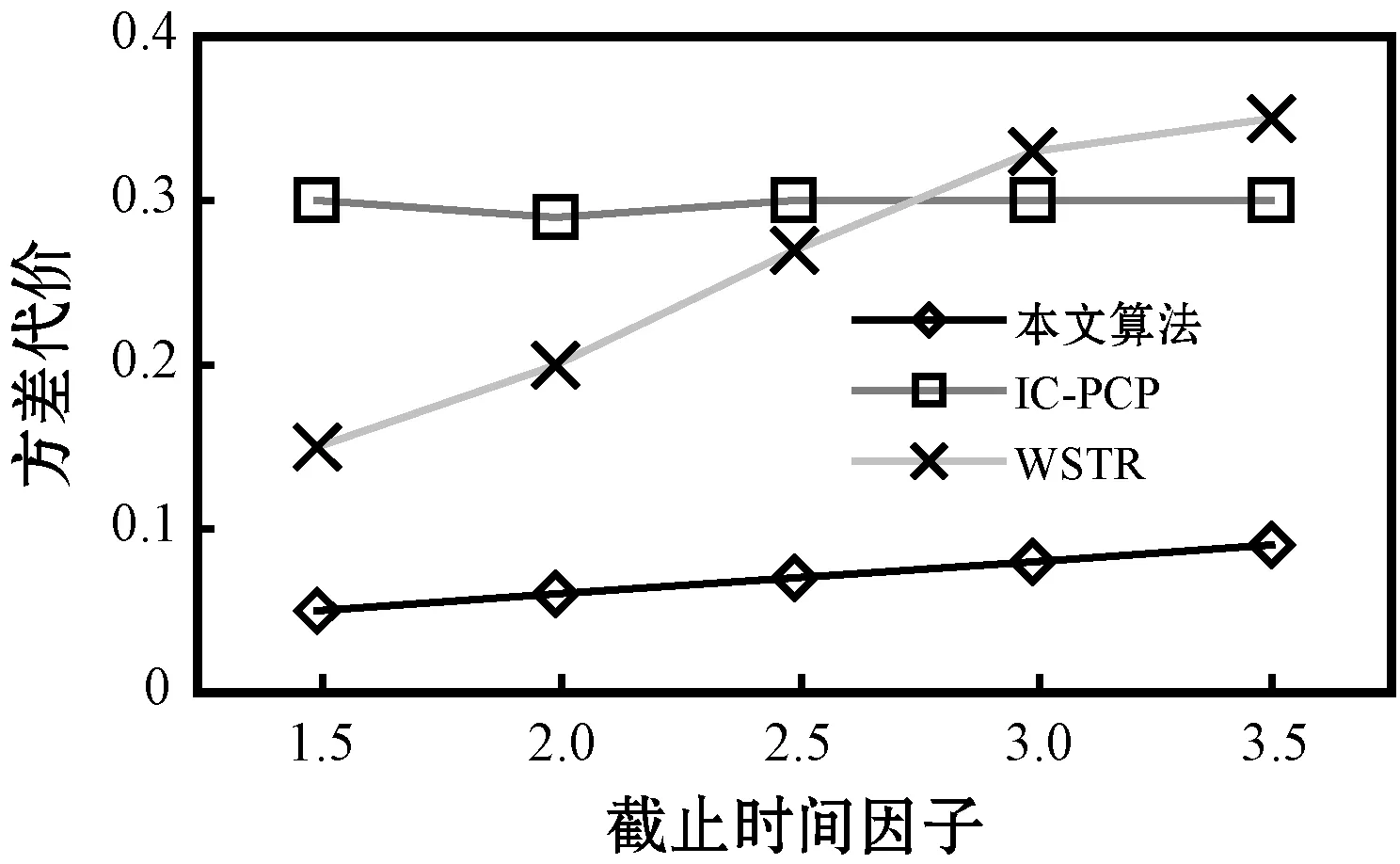
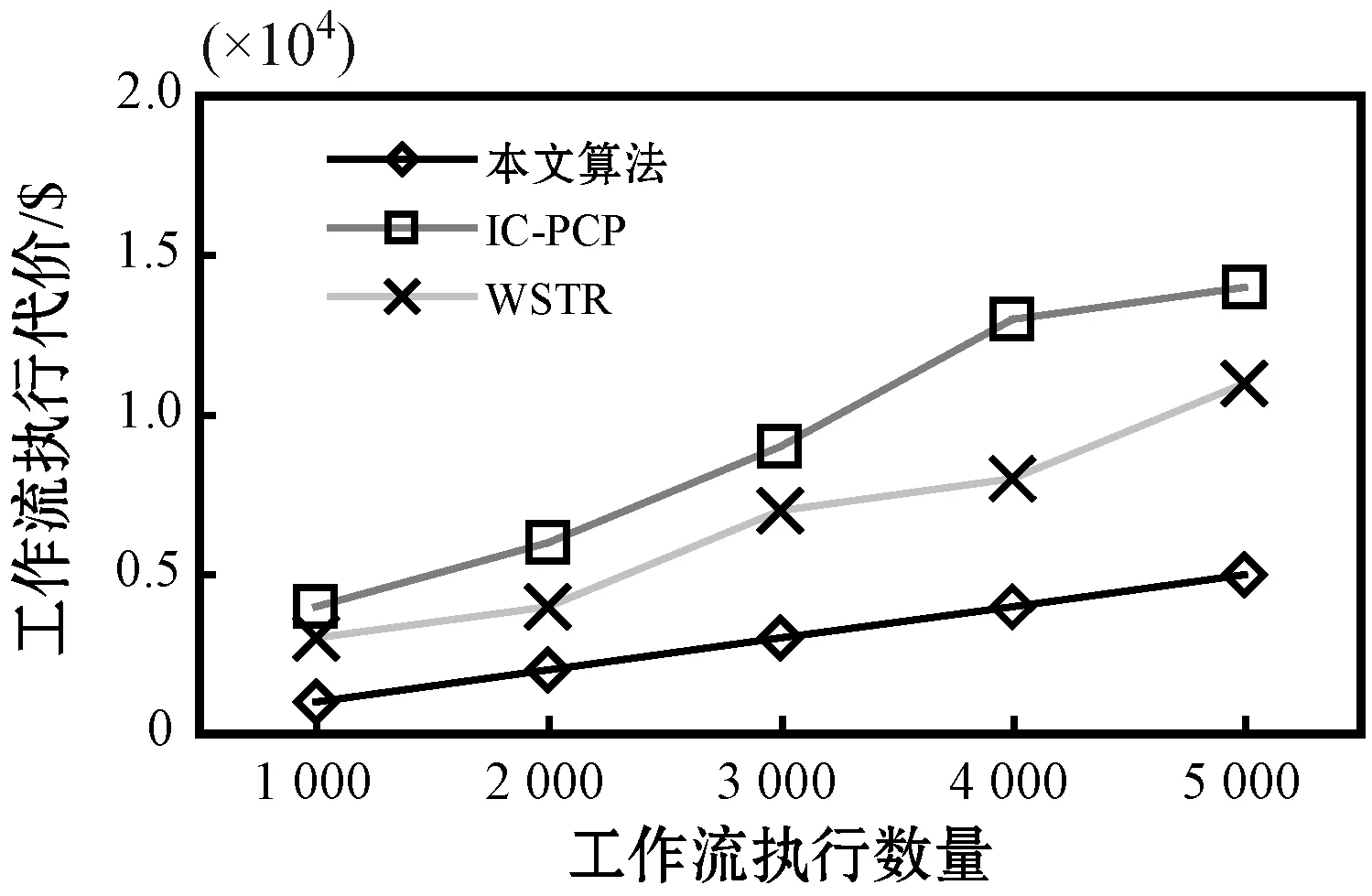
4.2 结论分析与比较
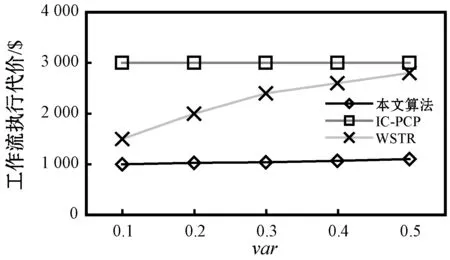
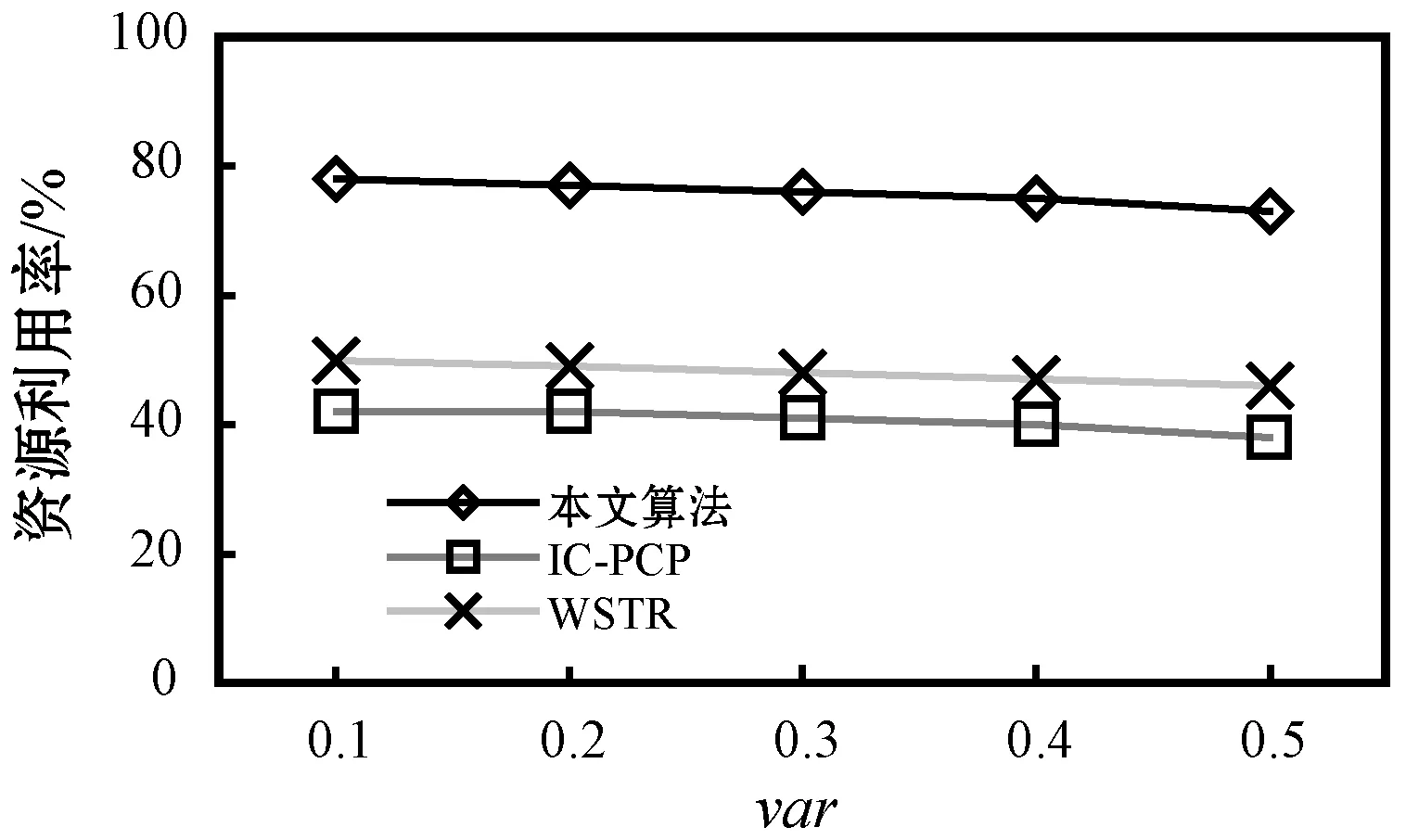
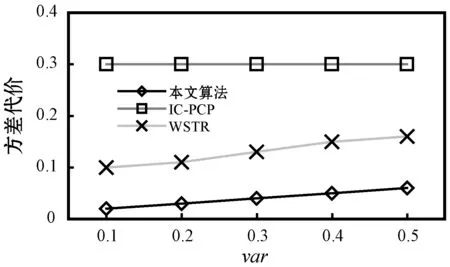




5 结 语

