基于生成对抗网络的混合类型数据生成方法
魏 宁 汪龙志 董方敏
(三峡大学计算机与信息学院 湖北 宜昌 443002)
0 引 言
在互联网时代,随着信息技术和人类生产生活交汇融合,大数据对经济发展、社会治理、人民生活产生了重大影响,通过大数据分析可以对用户群体的结构进行更合理的划分,从而提供更加精确的服务。但与此同时,当大数据平台将大量数据提供给外界进行数据分析时必然会增加用户隐私信息泄露的风险,这种风险对于金融和医疗等领域都是备受关注的焦点。为了降低隐私信息泄露的负面影响,美国、欧盟、中国等国家或组织不断通过完善隐私保护法规来对企业以及个人进行监管,以此来减少或者限制数据的共享和开放[1]。在这样的背景下,大数据分析研究常常会遇到数据匮乏、训练样本过少等问题。为了解决该问题,目前的研究思路主要是从信息隐藏和数据生成两个方面展开。从数据隐藏角度出发,如健康医疗组织(HCOs)通过泛化、抑制和随机化来干扰潜在的可识别属性然后再共享数据,以此来降低信息泄露的风险[2-3]。然而,不法分子依然可以通过剩余的属性信息还原数据对应的个人标签,从而恢复原始数据。而基于数据生成方法的研究,由于随着各种深度学习模型的建立,越来越受到该领域学者的关注,其主要思想是通过对极为有限的真实数据进行学习来捕捉数据集的潜在分布结构,然后通过生成模型来生成与真实数据具有相似分布的合成数据,以此来解决数据匮乏的问题[4]。本文的工作也是基于该思路展开,通过深度生成模型中的生成对抗网络来合成模拟真实的数据。
目前,深度生成模型被证实是一种高度灵活和可表达的无监督学习方法,能够捕获复杂高维数据的潜在结构。训练好的深度生成模型可以有效模拟高维数据复杂分布,生成与原始数据相似的合成数据[5-6]。与之相关的一些研究主要包括基于先验或后验的变分自编码器(Variational Autoencoder,VAE)[7],如变分有损自编码器(Variational Lossy Autoencoder)[8]、具有重叠变换的离散变分自编码器(DVAE++)[9]、形变化自编码器(ShapeVAE)[10],以及生成对抗网络(Generative Adversarial Networks,GANs)[11],如生成匹配网络(MMD-GAN)[12]、增强生成模型(AdaGAN)[13]和Wasserstein GAN(WGANs)[14]。其中生成对抗网络(GANs)近年在图像生成方向取得了丰富的成果,在生成逼真图像的性能上远超其他方法[15]。GANs模型采用对抗博弈的思想,由生成器G和鉴别器D两部分组成,生成器学习真实样本的分布并生成相似的合成数据,鉴别器判别真实数据和合成数据,两者互相进行对抗交替训练。随着生成对抗网络领域的实践应用与理论发展[16],越来越多的学者将关注点转向对数据科学的研究。目前与GANs相关的研究大多针对连续数据集,但是数据科学应用通常还涉及离散变量。对于这些数据,GANs从离散分布层采样是不可微分的,导致无法使用梯度反向传播训练模型,因此无法直接训练出具有分类输出的网络。Jang等[17]提出Gumbel-Softmax方法来解决变分自编码器(VAE)生成离散数据问题,与此同时Kingma等[18]也提出Concrete-Distribution方法来解决此问题。在基于VAE所提出的方法中,Kusner等[19]将这些方法应用到GANs模型来生成离散序列数据。针对同样问题,seqGAN[20]基于强化学习的思想提出随机策略方法以避免离散序列反向传播问题。另一种避免离散数据反向传播方法是Adversarially regularized autoencoders(ARAE)[21],将训练用的离散词项转换为连续的潜在特征空间,并利用GANs生成潜在的特征分布。Edward Choi等[22]提出一个与ARAE类似的Medical Generative Adversarial Network模型(medGAN)来生成合成二进制或数值类型数据。此模型基于Vincent等[23]提出一种基于编码器-解码器的方法,预先训练一个自编码器,编码器将样本映射到低维连续空间,解码器返回原始数据空间,然后利用GANs生成连续型数据的优势生成数据的低维连续空间,接着通过解码器解码出低维连续空间对应的高维连续或离散空间,增强模型生成合成数据的准确度。对于标签变量的生成,Ramiro等[24]在medGAN基础上提出一种多标签变量的生成对抗网络(Multi-Categorical GAN),其思想是将多标签变量编码为多个独热编码(One-Hot-Encodings)组合的二进制表示[25],并将Gumbel-Softmax这个针对变分自动编码器(VAE)领域中的方法应用到模型当中,提高计算稳定性和收敛速度。基于现有的VAEs无法直接处理混合类型数据,Alfredo等[26]提出一个HI-VAE似然生成模型来拟合混合类型数据,并通过ELOB证据下界来优化生成模型和识别模型的参数,以此来生成混合类型数据。
现有基于GANs的模型缺少针对于混合类型数据生成方面的研究。本文提出一种混合类型数据生成模型mixGAN,该模型通过自编码器将混合数据映射到低维连续空间,然后通过在低维空间中的生成器和原始空间的鉴别器进行联合对抗学习获得混合数据生成器,并构造出一个混合类型数据的损失重建函数。通过构造实验,本文生成模型能够捕获复杂高维数据的潜在结构,有效地模仿来自大型高维混合数据集的分布,保持了数据集的完整性和相关性,生成与原始数据集更加接近的新数据集。
1 本文方法和模型
1.1 数据预定义背景
本文假设数据的每个记录包含数值和标签两种类型,数据空间定义为S=(W×V),其中数值空间W=W1×…×WM(W∈RM),定义随机向量x=(x1,x2,…,xM)∈W;标签空间V=V1×…×VN,其中Vi为该属性所具有的所有类别(比如男女、职业等),每个标签的类别个数di=|Vi|,定义随机向量v=(v1,v2,…,vN)∈V,对其中每个标签向量vi经过One-Hot编码后记为向量yi∈{0,1}di。于是空间S中的随机变量s可以表示为s=(x,y)=(x1,x2,…,xM,y1,y2,…,yN),其中yi=(yi,1,yi,2,…,yi,di)。
1.2 本文模型
本文所提出的mixGAN首先预训练一个并行输出的自编码器(Autoencoder),通过它完成混合数据空间到低维连续空间的映射。然后通过建立在低维连续空间的生成网络G和建立在原始混合数据空间中的鉴别器D进行联合对抗学习获得最终需要的生成器G。本节将通过分别描述自编码器网络和生成对抗训练网络完成对mixGAN的各个模块的介绍。
1.2.1前置自编码器
本文针对自编码器的解码输出层进行修改,将混合层的数据进行切割输出,在其后放置N+1个并行的属性输出层,如图1所示。并行输出模型既保证了单属性的独立性也维持了属性间的相互依赖关系。自编码器的Encoder网络将输入的混合数据s=[x1,x2,…,xM;y1,y2,…,yN]映射到低维连续的编码空间(Code Space),然后自编码器的Decoder网络将编码空间数据投影回原始数据空间,完成数据重建。
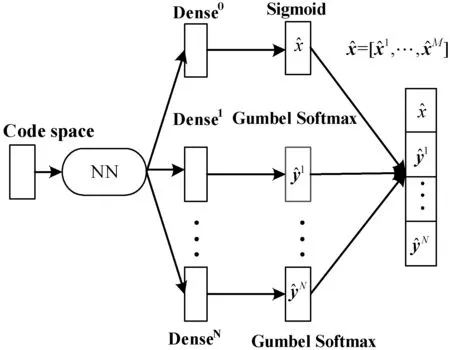
图1 Autoencoder自编码器
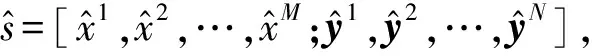
本文利用Gumbel-Softmax的采样技巧来对离散分布进行采样[17],解决离散数据反向传播问题。具体方法是将隐变量建模为服从离散的多项分布,转化过程满足下式:
(1)
式中:j=1,2,…,N,k=1,2,…,dj,ai为全连接层Dense1,Dense2,…,DenseN的输出,τ∈(0,∞)为大于零的超参数且控制着软化程度:τ值越高生成的分布越平滑;τ值越低生成的分布越接近离散的One-Hot分布。训练中过程中可以通过逐渐降低τ以逐步逼近真实的离散分布。
在模型训练期间,对Decoder网络的输出与原始数据进行对比,重建损失函数为式(2)。式(2)中,对于数值类型变量采用均方误差进行误差计算,对于分类变量采用交叉熵进行误差计算。数值类型数据在输入模型之前进行归一化处理,因此各个类型误差量级相同且在0到1内,不会出现大的误差量压制小的误差量。
(2)
式中:xm代表多数值向量x的第m个维度,yj,k代表多标签向量yj的第k个维度,B为训练批次的大小。
1.2.2生成对抗网络模型(GANs)
生成对抗网络由两个网络模块组成,生成器网络(Generator Network,G)和鉴别器网络(Discriminator Network,D)[10]。生成器G(z;θg)学习训练数据的分布,并将输入的随机先验分布转化为和训练数据相似分布的生成样本G(z)。鉴别器D(x;θd)是一个二分类器,用来判断所输入数据集是真实样本还是生成的假样本,即对于真实数据鉴别器将输出较大的概率,而对于假数据将输出较小的概率。在训练过程中使G和D互相博弈对抗,直到G生成的数据可以“骗过”D,上述的博弈过程的优化目标可表示为:
Ex~Pz[log(1-D(G(z)))]
(3)
式中:Pdata代表真实样本的分布,Pz代表服从N(0,1)的随机先验分布。在交替训练G和D的过程中参数优化遵循如下迭代公式:
(4)
(5)
式中:B为每个训练批次的大小,α为优化器的迭代步长。
1.2.3本文混合模型(mixGAN)
本文将自编码器应用到GANs的数据生成中,利用自编码器的解码器将低维连续的编码空间数据投影回原始空间。通过前置解码器,提升了模型的离散特征学习能力,又解决了离散数据反向传播问题。本文通过自编码器学习混合数据的特征空间,利用自编码器的解码器Dec将生成器G生成的潜在连续特征空间解码为原始混合数据空间,模型如图2所示。

图2 mixGAN模型视图
如图2所示,生成器G生成的数据在导入鉴别器之前先经过Dec(G(z))的解码,可以看到鉴别器D对数据真实性的判别是在原始空间中进行的,本文模型训练过程中生成器G和鉴别器D的损失函数构造如下:
(6)
(7)
在训练mixGAN模型时,预先训练好的解码器会内置到模型中,优化生成器G参数的同时微调解码器Dec可以看成是生成器G一个预训练好的隐藏神经单元。
2 实验与结果分析
基于目前最新的混合类型数据生成模型HI-VAE,本文以此为基准进行对比评估。HI-VAE在编码和解码时区分对待数据中不同属性类型,为每一种类型设计对应的概率模型。依据每一种属性所对应的概率模型,HI-VAE的编码器对该属性进行单独处理,并把所有的属性处理结果进行汇总而产生编码。HI-VAE的解码器则执行上述处理的反过程,即将编码转换为各个属性值并拼接在一起。
2.1 数值实现的实验
2.1.1数据集
本文实验对LendingClub开源银行数据集S={s1,s2,…,sk}进行训练和评估,样本总量为从中随机抽取的10 000行数据记录。每行数据si包含31个属性特征,剔除其中7个固定不变属性,并把相同类型属性归并到一起。si中代表分类类型的属性用One-Hot进行编码表示。数据集S进行预处理后si=[x1,x2,…,x15;y1,y2,…,y9],其中数值类型元素维度为15,Multi-One-Hot类型数据由9个One-Hot变量组成,每个标签变量的类别个数(One-Hot的位数)为[2,2,2,12,2,7,29,4,3]。
2.1.2数据归一化
原始混合数据集中,数值类型变量和标签类型变量量级相差较大,如果直接以原始数据集进行训练,量级大的类型就会在训练过程中占据主导地位,量级小的类型的作用就会被削弱,模型可靠性低。针对此问题,在训练之前对数值类型数据进行Min-Max标准化,使之与标签类型(One-Hot)变量量级相同,保证每个特征对训练结果的贡献相同,提升模型的精度,同时加快收敛速度。
2.1.3模型结果及参数设置
本文实验基于PyTorch 1.1环境完成。模型前向训练的自编码器基于Multilayer Perceptron(MLP)实现,Encoder和Decoder各自包含两个隐藏层,采用tanh函数激活。Encoder输出层输出的潜在特征空间维度设置为72,Decoder输出层采用Gumbel-Softma和Sigmoid激活。对于超参数τ,根据实验经验取0.666时可获得较好效果。GANs的生成器G和鉴别器D也是基于MLP实现,层与层之间利用Batch Norm进行归一化处理并进行残差连接,生成器G的隐藏层采用Tanh函数激活,鉴别器D的隐藏层采用LeakyReLU函数激活。模型优化都采用Adam算法,学习率lr设置为0.002,weight_decay设置为0.001,前置自编码器的训练时间为52.30 s,mixGAN模型训练时间为880.64 s。
2.2 结果评估
本文假设当所生成的数据和真实数据相似时应满足如下两个特点:① 在单个属性上,所生成的数据分布应该和真实数据的分布尽可能相似;② 生成数据在各个属性之间的依赖关系应该也和真实数据类似。基于以上假设,本文分别从属性独立分布和多属性相关性两方面来评估生成算法的优劣。
2.2.1属性独立分布评估
在对数据的属性独立分布进行评估时,本文按照数值类型属性和标签类型属性分别进行处理。对于数值类型的属性xi,首先将生成数据和真实数据在[0,1]区间内量化为10个等级,然后统计各自的直方图,之后将生成数据直方图和真实数据直方图按照等级进行配对(Preal,Pfake),如果二者分布相似则配对后的值应该接近相等。类似地,对于标签类型,分别统计生成数据和真实数据在属性yi,j上取值为1的概率,然后两两配对。当生成数据与真实数据在某个属性上分布相似时,则这些配对值应该近似相等。为评估这些配对值的相似性,图3以Pfake作为x轴、Preal作为y轴将这些配对点绘制到图中。图3(a)是本文所提出的mixGAN生成的数据与真实数据按照单个属性配对后绘制的点,图3(b)是文献[26]所提出的HI-VAE生成的数据与真实数据按照单个属性配对后绘制的点,其中圆形点代表标签类型,星形点代表数值类型。由之前的分析可知,点的分布越接近对角线则说明生成数据与真实数据在各个属性上越相似。从图3中的对比可以发现,在数值类型数据生成方面,本文所提出方法在属性独立分布方面明显要优于HI-VAE。

(a) mixGAN

(b) HI-VAE图3 生成数据与真实数据独立属性配对分布图
2.2.2多属性相关性评估
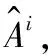
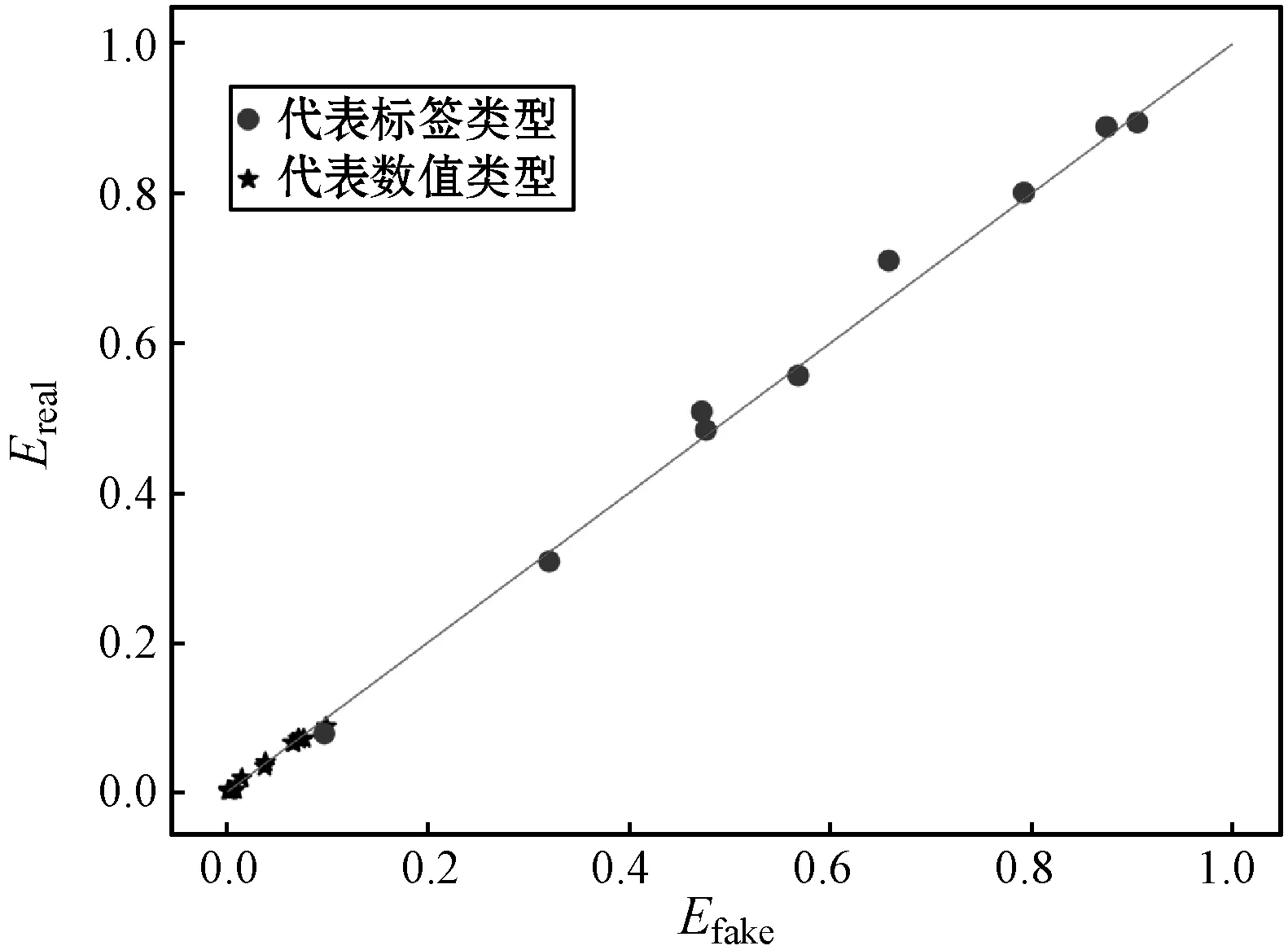
(a) mixGAN
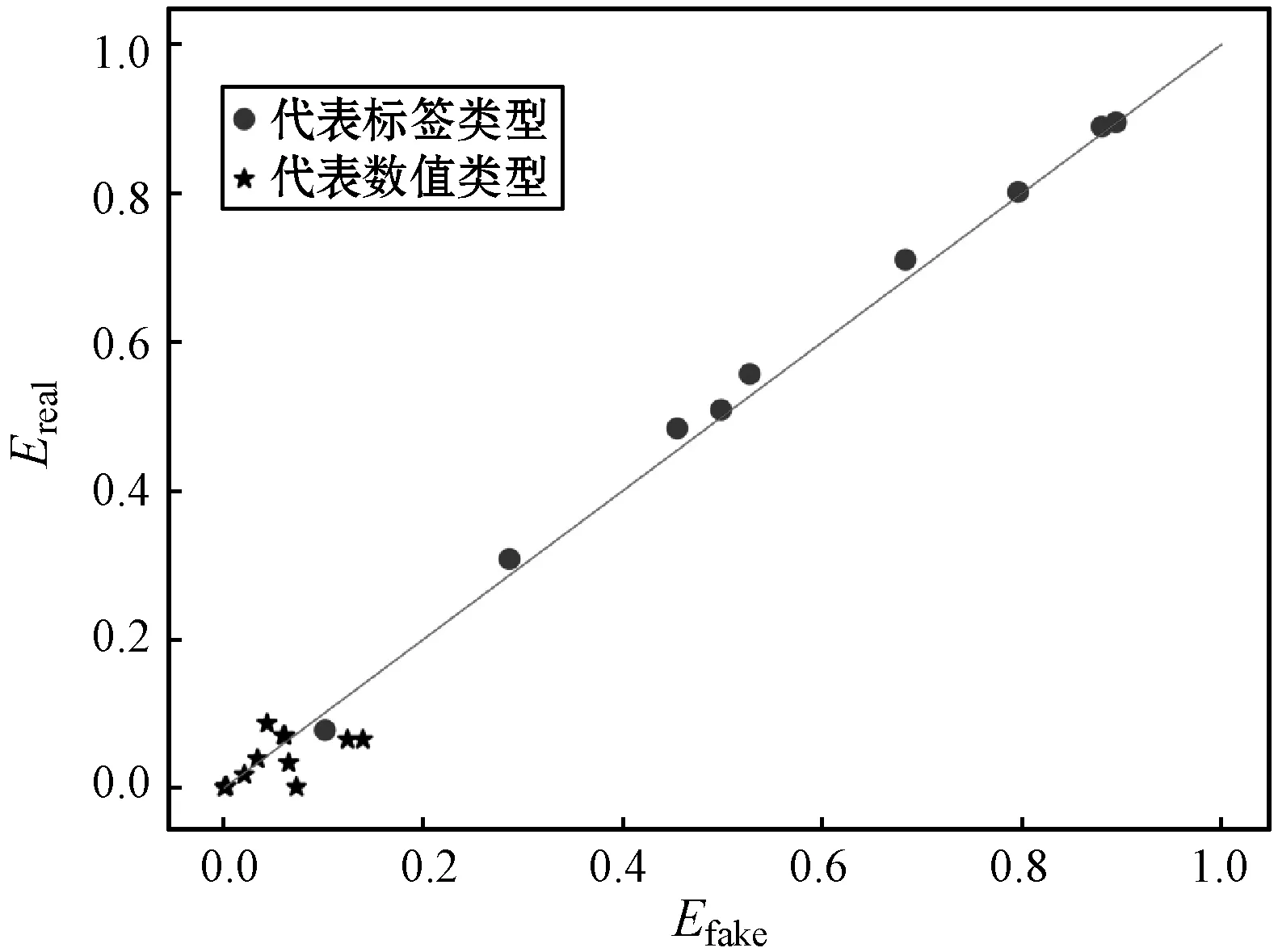
(b) HI-VAE图4 生成数据与真实数据多属性配对分布图
3 结 语
本文所提出的混合数据生成模型mixGAN,特别适用于数据科学领域对混合类型数据的生成的需求。算法成功将改进的自编码器应用到GANs模型中,提升了模型的离散特征学习能力。与现有的基于HI-VAE混合数据生成模型在属性独立分布和多属性相关性方面进行对比,本文方法性能都具有较为明显的优势,生成的结果与原始数据集的分布更加接近。下一步的工作重点将着眼于缺失数据的补缺。

