推荐系统中稀疏情景预测的特征-类别交互因子分解机

黄若然 崔 莉 韩传奇

1(中国科学院计算技术研究所泛在计算系统研究中心 北京 100190) 2(中国科学院大学计算机科学与技术学院 北京 101408)

推荐系统在网络搜索、在线广告和商业导购的发展中扮演了关键的角色，它解决了网络大数据给人们带来的“信息过载”问题，也为顾客提供了个性化信息服务和决策支持.一个成功的推荐系统能为客户提供高效的推荐服务，提高企业的生产利润，并产生相应的经济效益和社会效益.目前，推荐系统已成功应用在电子商务(如Amazon、阿里巴巴等)、社交网络(如Twitter、微博等)、电影推荐(如Netflix、豆瓣等)、音乐推荐(如LastFM、网易云音乐等)、新闻推荐(如今日头条、GoogleNews等)[1].

现有的个性化推荐系统面临的一个主要问题是数据的稀疏性.数据稀疏指的是用户往往只对比例很小的服务存在反馈，导致用户-物品的反馈矩阵非常稀疏，其稀疏度通常可达到99%以上[2]，即用户平均只与不到1%的服务有过历史交互.这使推荐系统难以有效地学习用户的偏好，无法生成准确的推荐列表.早期在稀疏数据上计算用户偏好的个性化推荐算法主要为逻辑斯谛回归(logistic regression, LR)[3]和支持向量机(support vector machines, SVM)[4]，但这类算法太过依赖人工特征工程，需要耗费大量的精力，导致计算效率低下.

为了更高效地解决因数据稀疏带来的人工特征繁琐和推荐精度不准确的问题，Rendle[5]提出了一种基于矩阵分解的机器学习算法：因子分解机(factorization machine, FM).FM通过构建特征的交叉组合，来学习用户-物品间潜在的交互关系.FM可以在非常稀疏的数据环境中进行丰富的特征交互计算，且可以应用于任何特征值为实值的情况.相比于其他因式分解模型只能用于一些输入数据比较固定的情况，FM更加通用和灵活.此后，为了进一步挖掘特征交互思想背后的价值，Juan等人[6]在FM的基础上引入了“类别”(或“场”)的概念，即“field”，并提出了类别因子分解机(field-aware factorization machine, FFM).FFM的主要思想是把相同性质的特征归于同一个类别，并单独进行热独(one-hot)编码，因此在FFM中每一个特征都会针对其他特征的每个类别学习一个隐变量，该隐变量不仅与特征相关，也与类别相关.

随着深度学习的迅速发展，He等人[7]在2017年提出了神经因子分解机(neural factorization machine, NFM)，NFM可以看作是FM的神经网络推广，它推迟了FM的实现过程，并在其中加入了更多非线性运算.相比于NFM，注意力因子分解机(attentional factorization machine, AFM)[8]则更多地关注特征交互间的权重计算，它为每一对交互特征分配一个所属的注意力因子，用以更好地区分不同特征间的重要程度来达到更好的预测效果.随后，Hong等人[9]受到FFM类别交互的启发，在AFM的基础上引入了类别交互的概念，提出了一种将特征和类别分别进行交互的模型——感知交互因子分解机(interaction-aware factorization machines, IFM)，并在多个领域取得了最优的效果.

本文在IFM的基础上，提出特征-类别交互机制(feature-over-field interaction mechanism, FIM)的概念，通过对特征向量和类别向量进行融合，并将融合后的向量两两配对交互，以获取更为丰富的交互语义信息.并以此为支持点，提出了新的因子分解机模型——特征-类别交互因子分解机(feature-over-field interaction factorization machine, FIFM).FIFM从特征交互角度、类别交互角度和特征-类别交互角度出发，更加全面地获取稀疏场景下的各类交互信息，进一步提高了预测效果.此外，为提高FIFM的泛化性使其适应多种复杂的数据场景，我们还提出了一种基于FIFM的神经网络版本——广义特征-类别交互模型(generalized feature-field interaction model, GFIM).相比于FIFM，GFIM的参数和时间复杂度更高，但同时也能捕获更多高阶的非线性特征交互信息，适合算力较高的应用场景.

本文的主要贡献有4方面：

1) 提出了一种将特征-类别融合后进行交互的机制FIM，使其可以学习特征-类别之间更为深层次的潜在语义信号;

2) 提出了一种面向稀疏情景的特征-类别交互因子分解机FIFM，它从特征交互、类别交互及特征-类别交互的视角出发，能够更加准确地预测稀疏条件下的用户意图;

3) 基于深度学习理论提出了一种FIFM的神经网络版本GFIM，相比于FIFM，GFIM的参数量和时间复杂度更高，但同时也能捕获更多高阶的非线性特征交互信息，适合高算力应用场景;

4) 在4个真实数据集上的实验结果表明相比于现有的主流模型，我们提出的模型能够在参数量近似的情况下，在均方根误差(RMSE)指标上取得更好的效果.

1 相关工作

1.1 基于机器学习的特征交互预测方法

FM是一种基于矩阵分解的机器学习算法，最大的特点是对于稀疏的数据具有很强的特征交互学习能力.FM通过对交互后特征的低秩展开，为每个特征构建隐式向量，并利用隐式向量的点乘结果来建模2个特征的组合关系，实现了对2阶特征组合的自动学习.值得注意的是，FFM的任意2组交叉特征的隐向量都是独立的，每一个特征都对应一个独一无二的类别，并为其分配一个隐向量，因此相比于FM的特征数乘以隐向量维度的参数量，它还多乘以一个类别数量，进而引入了更多的计算参数，为实际的运算带来不小的计算花销.而Chen等人[10]则从特征选择的角度，提出了一种基于FM的贝叶斯个性化特征交互选择算法，来筛选淘汰出那些在特征交互中效率较低的交互配对.通过在FM中集成贝叶斯个性化选择机制来进一步提高特征交互的效率.除此之外，另一种较为新颖的特征交互学习方法是将特征向量嵌入过程映射到可违反洛伦兹三角不等式的双曲空间当中[11]，由双曲三角形的特殊几何特性学习交互信息.

1.2 基于深度学习的特征交互预测方法

随着近几年深度学习在各个领域的成功应用[12-14]，基于深度学习的特征交互预测方法也相继被提出.为了能够直接利用神经网络层，Wang等人[15]提出了一种简单的结合方法——因子分解机支持神经网络(factorization machine supported neural network, FNN)，它直接将FM与多层感知机(mul-tilayer perceptron, MLP)进行串联组合，并采用FM预训练得到的隐含层及其权重作为神经网络第1层的初始值，之后再不断堆叠全连接层，最终输出预测结果.由于FNN嵌入权重的初始化是FM预训练好的，因此它不是一个端到端的训练过程.考虑到FM特征交互方法只进行嵌入向量的两两内积求和，因此该改进方法没有充分利用2阶特征组合的信息.He等人[7]提出了基于深度学习的神经因子分解机NFM，它的主要思想是利用2阶交互池化层(bi-interaction pooling, BIP)对FM嵌入后的向量两两进行元素级别的乘法，形成同维度的向量求和后作为前馈神经网络的输入.Guo等人[16]于2017年提出了DeepFM(deep factorization machine)模型，将深度学习的神经网络部分与FM相结合，用FM做特征间的低阶组合，用深度神经网络层(deep neural network, DNN)做特征间的高阶组合，通过并行的方式组合2种方法并获得了更精确的效果.Xiao等人[8]提出了一种注意力因子分解机AFM，该文作者认为现有的FM交互特征权重未做区分，不是所有特征交互都有同样的价值，相反低贡献度的交互特征可能会引入噪声.该文作者通过对FM不同的特征交互引入不同重要性因子来改善FM的学习方式.

1.3 基于特征交互和类别交互的预测方法

1.1节和1.2节提到的方法中，大多是针对于特征交互的预测方法，如FM，NFM，AFM，也有针对类别交互的预测方法，如FFM.基于此，Hong等人[9]提出将特征交互和类别交互进行融合的IFM，并利用交互后的感知向量共同作用于预测结果.IFM由于其优异的表现效果，现已成为稀疏特征预测方法中的重要对比方法.

本文在IFM分别将特征交互和类别交互独立交互的基础上，提出了一种特征-类别融合交互的新机制FIM，用以进一步增强交互信息在稀疏条件下的预测结果.FIM不仅可以对IFM进行信息增益，还可以与其他FM模型进行衔接，在时间和空间的消耗均与主流模型接近的情况下提高其他FM模型在各自适用领域内的精度.

2 因子分解机(FM)和类别因子分解机(FFM)

2.1 基于特征交互的FM相关描述及定义

传统的SVM难以解决特征稀疏问题，FM主要是为了解决数据稀疏的情况下特征怎样组合的问题.FM的主要思想是利用多维特征之间的交叉关系，利用矩阵分解的方法进行参数的训练.基本的符号表示为:

假定每一条训练数据拥有特征属性x={x1,x2,…,xm}，其中xi表示第i个真实的特征值，m表示特征的数量，它的真实值y可代表用户是否进行了点击(或选择).非零特征交互对表示为

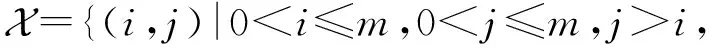
(1)

(2)

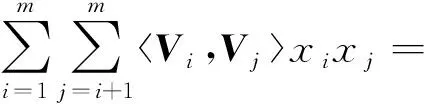
(3)

2.2 基于类别交互的类别因子分解机(FFM)

为了将交互操作扩展到其他维度，FFM在FM的基础上对同一个类别特征单独进行one-hot编码，使得特征在交互时能够捕获更多关于类别的学习向量，通过增加可学习的参数空间来提升效果.

假设样本的m个特征属于f个类别，那么FFM的二次项有mf个隐向量.而FM模型中，每一维特征的隐向量只有一个.FFM的模型方程为

(4)

如果隐向量的特征维度为d，那么FFM的二次参数则有mfd个，远多于FM模型的md个.由于FFM参数较多，在实际的运行中需要极大的算力作为支撑，因此为其在工业界的应用和推广带来了不小的挑战.

3 特征-类别交互因子分解机

3.1 神经因子分解机(NFM)

传统FM只学习到了2阶交叉特征和线性回归特征等此类低阶信息，未对深层次信号做进一步的挖掘.NFM通过对FM做神经网络扩展并添加了更多的非线性运算来进一步提升深层信号的获取能力.NFM的网络结构如图1所示:

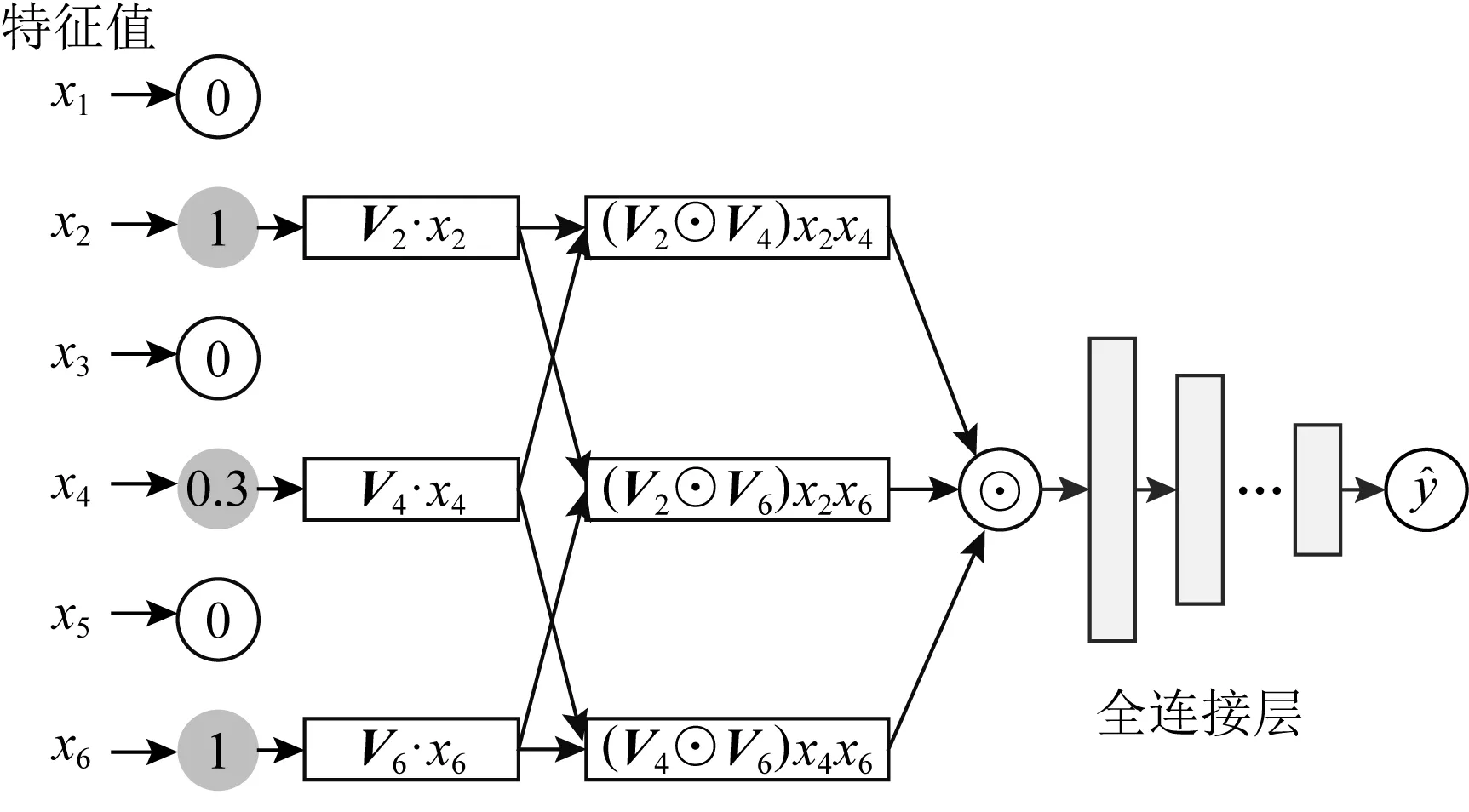
Fig. 1 The network architecture of NFM图1 NFM的网络架构

相比于FM，NFM采用2阶池化层结构来对2阶交叉信息进行处理，使交叉特征的信息能更好地被DNN结构学习，降低DNN学习更高阶交叉特征信息的难度.我们将NFM的2阶交互部分归纳为

(5)

式(5)为NFM的核心思想(为方便表示，我们省略其线性部分).即对FM嵌入后的向量两两进行元素级别的乘法，形成同维度的向量求和后作为前馈神经网络的输入，⊙表示逐元素乘法运算.在计算完式(5)后得到一个维度为d的向量，图1中还使用了多层感知机以捕获更为高阶的交互信号.

3.2 注意力因子分解机(AFM)

相比于NFM，AFM[8]则更加着重于特征交互间的权重计算.它的主要思想是通过在逐元素乘法之后形成的向量进行加权求和，权重是基于网络自身产生的.此方法是引入一个注意力子网络(attention net).AFM的网络结构如图2所示:

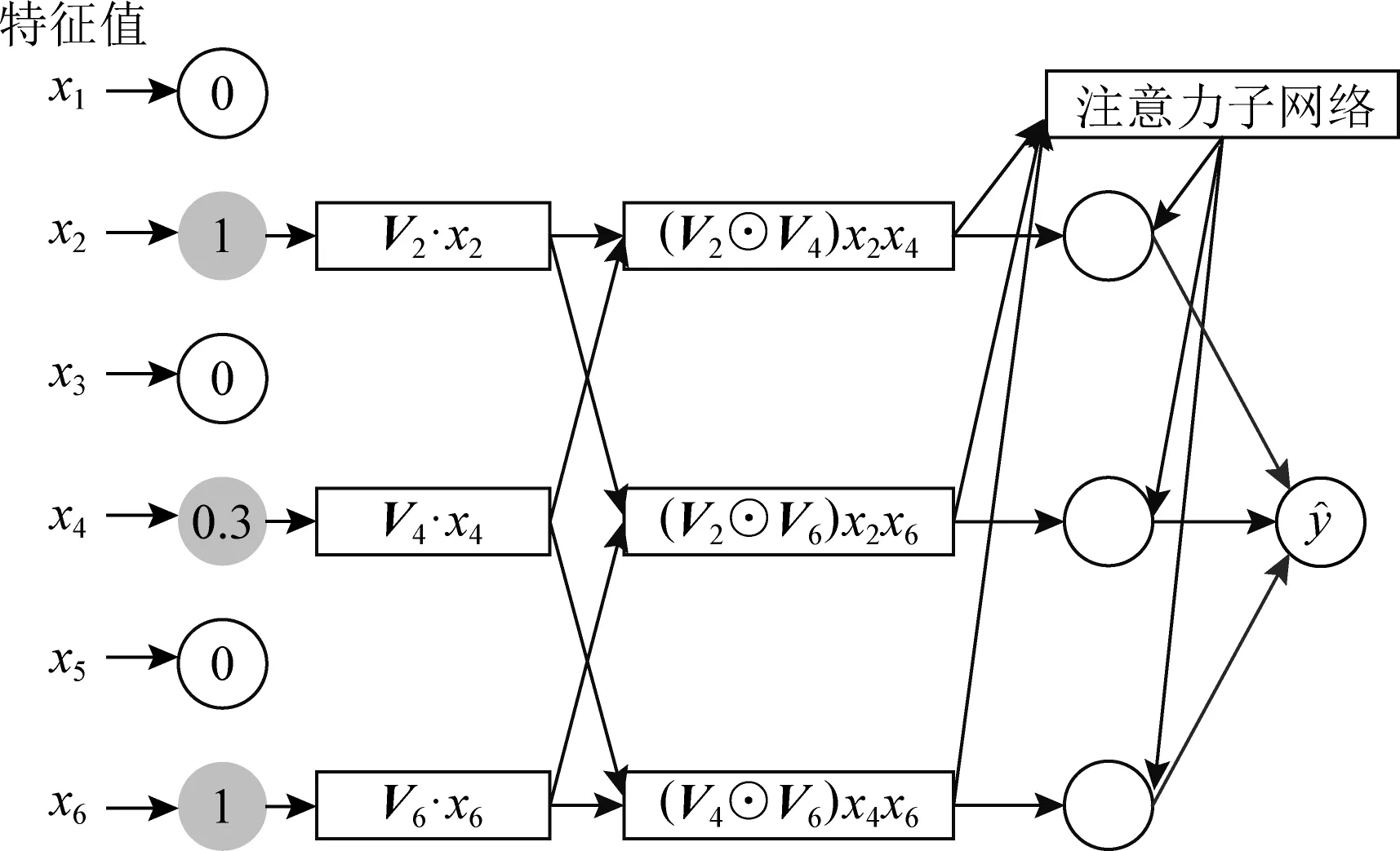
Fig. 2 The network architecture of AFM图2 AFM的网络架构

由图2可以看到，右上角的注意力子网络是相比于NFM多出的部分，并且AFM没有MLP部分，当权重都相等时，AFM退化成无全连接层的NFM.AFM的预测值为

(6)

其中αij负责为每一对交叉项分配权重，是特征xi和特征xj进行配对交互时对应的注意力因子，用以衡量二者之间的特征重要程度.其计算过程为

hij=MTReLU(W1(Vi⊙Vj)xixj+b1)，

(7)

(8)

其中，W1∈Ka×d，M∈Ka×1，b1∈Ka分别表示权重转换矩阵、转换向量和偏置项，Ka表示注意力网络中隐藏层的单元维度，η控制收缩性.

3.3 感知交互因子分解机(IFM)

受到FFM类别概念的启发，IFM在AFM的基础上提出了使用类别感知交互(field-aware inter-action, FAI)来进一步影响交互特征，使其能从类别领域出发发挥预测作用.IFM的网络结构如图3所示.

图3所示的IFM对比图2所示的AFM，增加了虚线框中的FAI.这里的类别与FFM中“类别”的实现有所不同，FFM是为每一个特征分配与其他特征所在类别相对应的隐变量；而IFM中的类别则认为是当前一个特征下对应一个类别，交互只在特征对应的类别上实现.因此相比FFM，IFM所需要的参数量更少，其结合AFM中的特征交互部分得到：

(9)

其中，fi为特征xi的类别，Ffi,fj表示维度为KF的特征xi和特征xj所属类别的类别交互向量，用以计算类别级别的关系.

3.4 特征-类别交互机制(FIM)

从3.1～3.3节中FM系列的演化历史我们可以知道：NFM比原始FM多了2阶池化层，AFM在NFM的基础上为每一对特征交互增加了注意力网络，IFM则在AFM的架构上添加了类别感知交互.FM，NFM，AFM都是针对特征交互的预测，而IFM则是在特征和类别分别交互的基础上进行预测.

本文中所提出的FIM则是基于IFM增加了特征-类别融合，并对融合后的向量进行两两配对交互.该交互过程后有2种呈现模式：1)矩阵乘法，即FIM最终输出为每一对交互结果的标量值eij；2)让每一对特征-类别融合后的交互以元素逐点相乘的形式出现，即向量Eij，用于输入更为复杂的时间网络结构.针对这2种FIM对每对交互的输出形式——元素级eij和向量级Eij，我们提出2种相对应的模型，即FIFM和GFIM.图4展示了FIFM的网络架构.

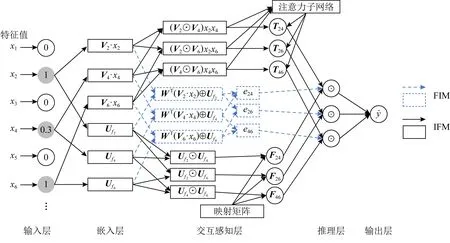
Fig. 4 The network architecture of FIFM图4 FIFM的网络架构

不同于FFM靠增加隐式的参数来学习潜在的field信息，FIM显式地学习特征和类别之间的关联，降低了学习的成本.为了方便理解，我们将式(9)重新定义为

(10)

其中，第1个“1”表示融合特征和类别交互后的权重系数，第2个黑斜体“1”表示类别交互向量，第3个“1”表示特征交互的注意力系数.至此，我们在IFM的基础上提出特征类别机制，它综合了特征、类别及特征-类别3种不同的交互视角，我们可将此过程扩展为

(11)

相比式(9)，我们增加了元素特征值eij，用于学习特征-类别后更深层次的隐藏信息，并衡量IFM中特征部分和类别部分组合时的重要性.

Ffi,fj=HT(Ufi⊙Ufj),

(12)

其中，H∈d×KF，U∈n×KF，而KF是H和U隐藏因子的神经元数量.通过式(12)的分解，类别交互的复杂度可以由线性关系表示：d×KF+KF×n.

从式(12)中可以看到，类别交互学习同原始的因子分解机中的2阶特征交互(Vi⊙Vj)xixj具有相似的结构.由于最终的维度相同，这2种结构是可以相互影响和计算的.这2种结构映射为双线性关系:

simH(C,G)=CTHG,

(13)

其中，C=Ufi⊙Ufj，G=(Vi⊙Vj)xixj.

在获取到特征交互和类别交互之后，本工作对潜在影响因子进行了进一步的挖掘，即融合特征-类别向量，并为其赋予一定的学习参数，使其能够在拥有特征-类别混合信息的同时还能进行2阶交互，提高预测精度.此操作会带来4个效果：

1) 学习特征-类别之间更为深层次的潜在语义信号，这些语义信号能够为IFM中特征交互和类别交互在预测阶段带来信息增益，提高预测精度.

2) 融合后的特征-类别向量也可以看作是一个汇集了特征-类别信息的新向量，在2阶交互后自身也具有一定的信息预测能力，属于特征-类别概念中新的衍生模型.

3) 由于FIM的输出是按特征或类别交互进行逐一配对的(关于i,j索引)，因此FIM可以和其他FM模型无缝衔接以增强预测能力.

4) 特征-类别的融合是基于已有的特征向量和类别向量，除了融合时的学习参数外，不会增加额外的空间负担.在时间复杂度上也仅维持在2阶向量交互的级别，与NFM的2阶池化操作保持相同.

针对于上述4个效果，我们会在第4节实验1～3的结果分析中逐一进行验证.

实现特征和类别的融合，我们需要将二者的维度进行统一，由于KF≪d，考虑到计算的时间和空间复杂度，对xi所对应的原始向量Vi做一个线性变换：WT(Vi·xi)，其中W∈KF×d，之后将其与类别嵌入向量做逐点相加操作.特征和类别的融合向量可以表示为:

Ri=WT(Vi·xi)⊕Ufi，

(14)

⊕表示向量间的逐点相加.由于类别特征向量是按照特征-类别进行划分的，即它本身就拥有n个类别，即对应n个非零值，因此我们也可以对其进行两两交互.鉴于式(14)已可以分别求得特征交互向量G和类别交互向量C.因此，只需要计算二者结合的向量Ri即可得到两两交互的权值影响因子:

eij=Ri·Rj，

(15)

对于式(15),除了为每一对交互向量获取元素级别的融合交互特征eij外，还可通过元素逐点相乘，为每一对特征交互或类别交互获取对应交互向量.

Eij=Ri⊙Rj，

(16)

交互向量相比于交互特征具有更为丰富的信息单元，可用于场景数据更为复杂的高阶神经网络预测.

3.5 特征-类别交互因子分解机(FIFM)

3.5.1 FIFM的网络架构

FIFM通过引入3.4节中的FIM来模型化特征交互.图4展示了FIFM的网络架构.

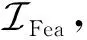
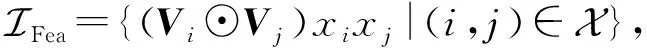
(17)

(18)

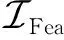
(19)

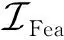
(20)

3.5.2 模型训练

FIFM的目标主要为推荐系统中的一系列预测任务，可分为二分类、回归和排序等.对于二分类任务，常用的损失函数为对数损失(log loss)[17]；对于回归任务，常用的损失函数为平方损失.同NFM，DeepFM，AFM，IFM类似，本文主要讨论回归任务并优化平方损失.相似的策略也可以用于分类和排序任务.针对目标函数，我们采用了梯度下降算法中的AdaGrad[18]优化器来迭代地计算每一轮参数的值.为了防止模型过拟合，在模型中为嵌入矩阵V和U添加了L2[19]正则，并且在神经元的计算过程中使用了Dropout[20]技术来进一步规范模型的训练过程，并加快训练速度.目标函数定义为:

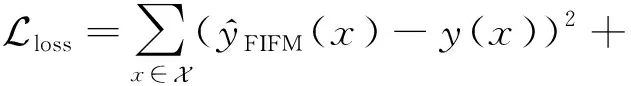
(21)

其中，λ和γ分别用于控制嵌入矩阵V和U的正则化学习率.FIFM模型的算法流程如算法1所示:

算法1.FIFM算法描述.

① 初始化参数矩阵V，M，H，U，W，W1;

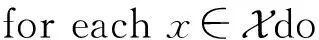
③ 根据式(6)～(8)计算特征交互向量αij·Vi⊙Vj;

④ 根据式(12)计算类别交互向量Ffi,fj;

⑤ 根据式(14)和式(15)计算特征-类别融合交互标量eij;

⑦ 根据式(21)计算损失函数;

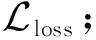
⑨ end for

3.5.3 FIFM的时空复杂度

1) 空间复杂度分析(space complexity analysis)

对于嵌入矩阵V的参数量为O(m×d)，而类别嵌入矩阵U，除原有的O(n×KF)参数量外，还有式(12)带来的O(d×KF)参数量.式(7)和式(8)的注意力子网络引入了参数量O(d×Ka+2×Ka).此外，式(14)引入了O(d×KF)的参数量.因此总的参数量为O(2Ka+(2KF+m+Ka)d+nKF)，由于Ka和KF一般均小于d且n≪m，因此在特征数m较大，即数据足够稀疏的情况下，总的参数量可近似为原始的FM参数量O(md).值得注意的是，本文的主要对比模型IFM[9]，在文献[9]中分析指出了空间复杂度的消耗也近似为O(md).相比IFM，FIFM增加的参数消耗主要来源于式(14)中的W∈KF×d，因此FIFM比IFM增加的空间消耗维持在一个以d为变量的线性函数上.

2) 时间复杂度分析(time complexity analysis)

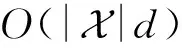
3.6 广义特征-类别交互模型(GFIM)

针对提出的FIFM，可在此基础上应用深度神经网络(DNN)进行进一步拓展，以更好地学习高阶特征交互.为此，我们对式(17)～(19)做一个神经网络下的新定义，将各自独立为神经网络学习中的向量模块.特征向量集合和类别向量集合分别定义为:

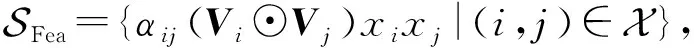
(22)

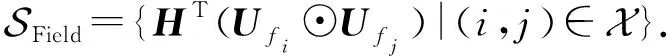
(23)

对于特征-类别融合的标量集合，我们将其扩充到向量级别,以更好地适应神经网络的学习过程:

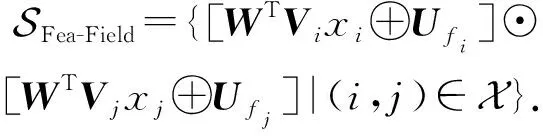
(24)

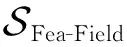
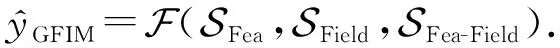
(25)

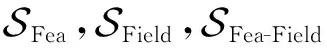
(26)

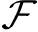
P0=SFea(c)⊕SField(c)⊕[SFea-Field(c)·Ws],

(27)

Pl=σ(QlPl-1+zl)，

(28)

其中Ws∈KF×d，σ为神经网络的非线性激活函数，本文选取ReLU[21]神经元的激活函数.

令rl代表第l层的神经元个数，则有Ql∈rl×r(l-1)，zl∈rl分别表示第l层神经元的映射矩阵和偏置项.

Pl∈rl代表第l层的隐藏层输出，由此，GFIM可表示为：

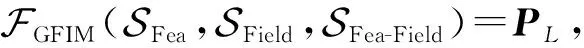
(29)

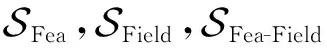
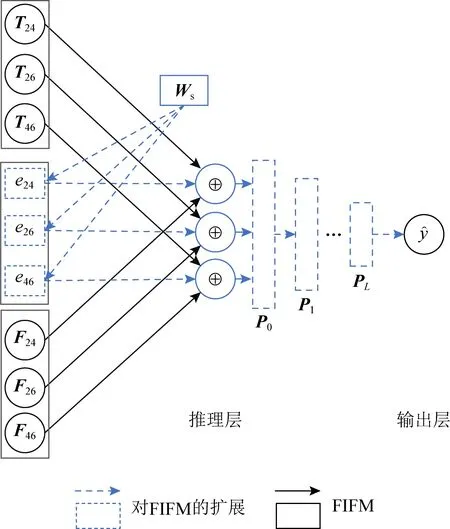
Fig. 5 The inference structure of GFIM图5 GFIM推理部分的结构

GFIM模型算法流程如算法2所示：

算法2.GFIM算法描述.

① 初始化参数矩阵V，M，H，U，W，W1，Ws，Q；

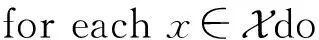
⑥ 通过式(27)计算融合后的特征向量P0；

⑦ for eachlinLdo

⑧ 执行式(28)以获取每轮神经网络迭代后的向量Pl；

⑨ end for

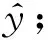
3.7 与主流模型之间的特性比较

为了更好地展现本文所提出的FIFM和GFIM的特点，我们列出了其余6种主流的FM模型，并比较了它们的相关特性，详细内容如表1所示:

Table 1 Comparison of Characteristics AmongDifferent Models表1 不同模型间的特性比较

4 实验与结果

为了证明本文提出的FIFM和GFIM的有效性,本文在真实数据集上进行验证实验,并将其结果与其他主流模型进行对比分析.

4.1 数据集介绍

本文面向情景预测选用了4个真实的稀疏数据集：MovieLens[22]，Frappe[23]，Book-Crossing[24]，Criteo[25].MovieLens中记录了来自90 445个特征的2 006 859条用户物品交互记录，其稀疏度为99.99%.Frappe记录了5 382个特征的288 606条用户物品交互记录，其稀疏度为99.81%.Book-Crossing记录了来自Book-Crossing读书网站的用户信息，其中包含来自6个类别的226 336个特征，共计1 213 367条记录.Criteo是一个来自Kaggle竞赛的CTR预测数据集，共有来自39个类别的662 913个特征，共计51 871 397条记录.由于Criteo的数据均为匿名处理后的LIBSVM格式数据，无法获知具体的用户及物品数，也无法计算稀疏度.为了保证实验的公平性，我们采用了与NFM和IFM相同的实验设计，整个数据集被划分为训练集(70%)、验证集(20%)和测试集(10%).所有的模型在训练集上进行训练，并在验证集上优化和调整训练结果.由于4个数据集都只包含了正样例，为保证训练的合理性，我们随机为每个正样例采样2个负样例进行配对训练.具体来说，对于MovieLens数据集，我们会随机采样2个用户未对电影打过的标签；对于Frappe和Book-Crossing数据集，我们将随机抽样2个用户未交互过的物品进行配对；对于Criteo数据集，我们沿用了原数据集中已经存在的对应比例正负样本配对实例.对于每个正样例，我们将目标值设置为1；而对于负样例，我们将目标值设置为-1.表2记录了4个数据集详细的统计信息.

Table 2 Statistics of Datasets表2 数据集统计信息

4.2 度量标准

在主流的推荐系统预测指标评测中，平均绝对误值差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)是评分预测任务的常用评价指标.考虑到RMSE相比MAE受异常值的影响更大，能更好地反映实验效果，因此在本文中，我们选取RMSE来评价具体的模型性能.RMSE的主要思想是通过计算预测值与真实值之间的差异来衡量推荐算法的准确性，其值越小，推荐的性能越好:

(30)

其中，N表示测试集记录条数，yi代表真实目标值.

4.3 对比模型

为了验证本文所提出的FIM模型在预测过程中的最终效果，本文选取6种经典的相关领域预测模型进行对比.

1) LibFM[5]是原始FM的官方实现版本,也是当前经典的推荐预测模型对比模型之一.

2) NFM[7]模型将矩阵分解模型与神经网络相结合,用于提取项目2阶线性特征及高阶非线性特征.

3) FFM[6]在FM的基础上了扩展了“field”的概念，它将每一个特征(feature)都归属于一个特定类别.类别与特征是一对多的关系，在学习时通过构造3维的类别-特征-维度嵌入矩阵来进行向量学习.

4) DeepFM[16]通过引入神经网络来对2阶以上的特征交互进行建模.它主要由FM和DNN这2部分组成，分别学习低阶和高阶的特征交叉关系，底部共享嵌入向量的权重输入.

5) AFM[8]通过对FM不同的特征交互引入不同重要性因子来改善FM，重要性因子由注意力网络学习得到.

6) IFM[9]通过构建特征和类别各自的交互向量，来分别学习不同领域的交互信息.

4.4 参数设置

为保证实验的公平性，所有的模型均在平方差损失函数下进行学习和优化.同NFM和IFM一样，我们将学习率的取值范围设置为{0.005,0.01,0.02,0.05}，并取其中最好的值进行预测.同时，为了防止过拟合，我们也对L2正则和Dropout率进行了取值上的微调.对于L2，其λ和γ取值范围可选取为{1E-6,1E-5,1E-4,…,1E-1}.而对于Dropout率，其取值范围为{0,0.1,0.2,…,0.9}.所有模型均使用AdaGrad[18]优化器进行优化.同时，对于Movie-Lens，Frappe，Book-Crossing，Criteo，每批次的训练数量依次为1 024，128，256，64，这些数量依据实验条件在不同数据集下的可计算性而定.所有模型嵌入层的向量维度默认为256.同IFM一样，我们将η的默认值设置为10.未提及的其他参数会保留原有的参数设置并进行适当的微调.其中，我们将KF的值分别在MovieLens和Frappe上设置为8和32以获得最佳效果.在Book-Crossing和Criteo数据集上，KF设置为16.我们将实验的默认迭代数设置为40，并采用Early Stop策略，即当模型在验证集上连续5次未超过当前已记录下的最好结果，便停止训练.

4.5 实验运行环境

1) 硬件环境.本文所有实验均在同一Linux服务器环境下进行测试.CPU为Intel®Xeon®Silver 4114@2.20 GHz，显卡为NVIDIA GeForce RTX 2080 Ti(显存容量11 GB，显存位宽352 b，显存频率1 4000 MHz)，内存为32 GB 2 666 MHz DDR4.

2) 软件环境.实验的系统环境为Ubuntu 16.04.实验编程语言为python 3.6.5，相关的深度学习框架为tensorflow，CUDA及cuDNN的环境分别为10.0和7.4.CPU环境运行下的编译器为GCC 4.8.为了支持实验的数据预处理以及相关的统计和分析工作，我们还引入了相关的Python科学计算包，具体用到的版本是：tensorflow(1.14.0),numpy(1.17.4),matplotlib(3.0.2),pandas(0.23.4),scikit-learn(0.20.1).

4.6 实验结果与分析

实验1.不同模型的性能比较.

如表3所示，我们将所有的模型在4个通用数据集上进行了比较，并列出了每一个模型所需的参数量.为了增强实验的说服力，我们给出了10次实验结果的平均值和实验方差，以“±”连接，作为最终结果.为方便区分，我们将本文提出的模型进行了加粗标记.由于FFM模型在Criteo数据集上的参数量过大，不便于在当前实验环境下计算，故我们在此未列出其结果.从结果中我们可以看到，FIFM模型及其扩展版本GFIM在所有比较模型中均获得最好的表现.其中，FIFM的平均表现在MovieLens，Frappe，Book-Crossing，Criteo数据集上分别比次最优的IFM模型提升1.32%，0.48%，0.67%，1.62%.而GFIM的平均表现在MovieLens，Frappe，Book-Crossing，Criteo数据集上分别比IFM提升3.26%，1.65%，1.17%，2.19%(对应3.4节的效果1).虽然看起来这样的提升指标并不明显，但需要指出的是，即使1%的性能提升也可能在实际应用中带来巨大的经济收益[12].而对于DeepFM，其在MovieLens及Frappe数据集上的表现差于NFM，而在Book-Crossing及Criteo上实验结果反超NFM.这得益于DeepFM的2阶交互和MLP的并行预测机制，相比于NFM串行的2阶交互池化层在训练时需要的信息量更多，因此在Book-Crossing和Criteo这种涵盖较为丰富信息的大参数量数据集下更容易捕获潜在的影响因子.DeepFM在Criteo上还超过了AFM，因此DeepFM可适用于大数据量环境下的工业预测.对于FIFM及GFIM，它们在所有数据集上都能有较为稳定的表现，且都优于其他主流的因子分解机模型，验证了我们模型的准确性.同时我们所提出的2个模型相比主流模型引入的额外参数量十分有限，且随着数据记录规模的增加(例如Criteo和MovieLens的记录远大于Frappe)，额外的参数花销占比会越来越小，但带来的表现增益却依然得到了不小的提升(对应3.4节的效果4的参数占用).

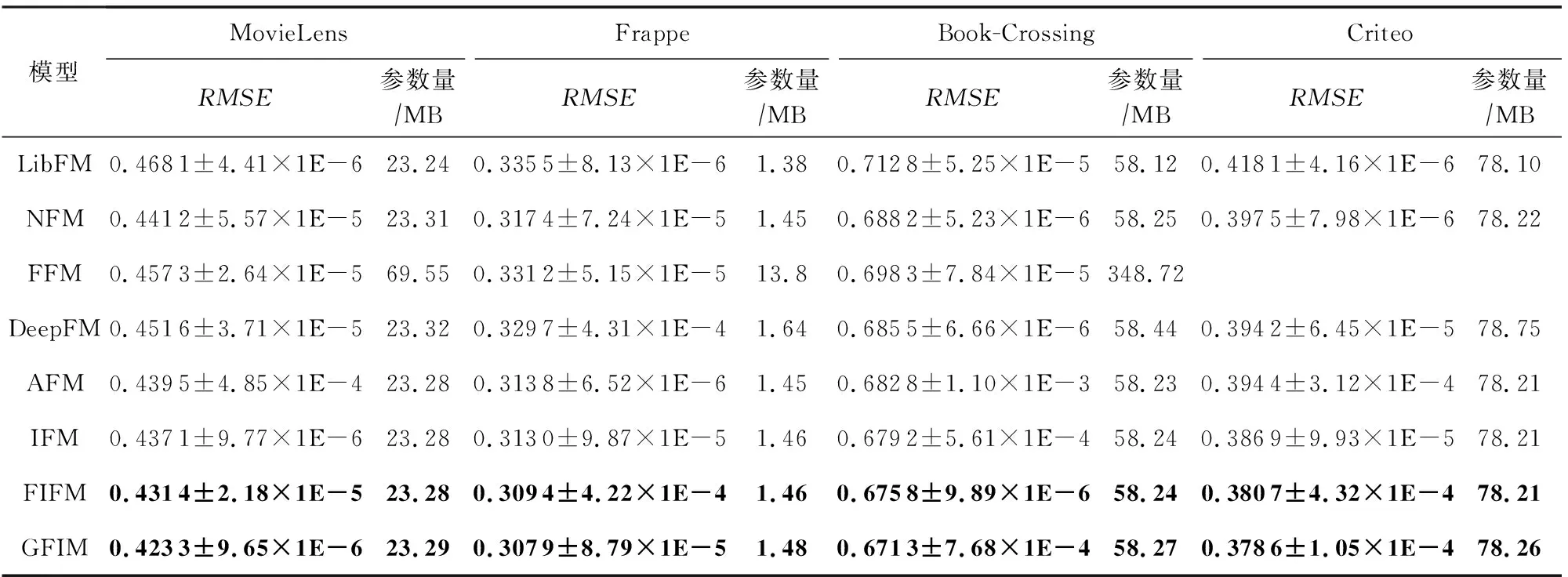
Table 3 Performance Comparison of Different Models表3 不同模型的性能比较

需要指出的是，GFIM相比于FIFM引入了神经网络，具有更强的泛化能力，因此也需要消耗更多的参数.但相比于同样引入field概念的FFM，参数量却减少了很多.不同于FFM为每一个特征的每一个领域分配一个独立的d维嵌入向量，我们的模型为每一个类别单独分配一个低维度的向量进行独立交互学习，极大降低了所需的向量空间.并且提出的FIM又进一步对特征和类别之间所存在的潜在关系进行更深层次的挖掘，提高了表现效果，这也是本文区别于其他主流模型的根本所在.

实验2.FIM的影响.

为了验证FIM的有效性，我们进行了基于FIM的消融实验.FIM-*代表FIM分别在不同种类的FM模型进行对应组合，此时式(14)中的W会因维度需要而进行变更.此外，FIFM也可以理解为FIM+IFM版本.实验结果如表4所示：

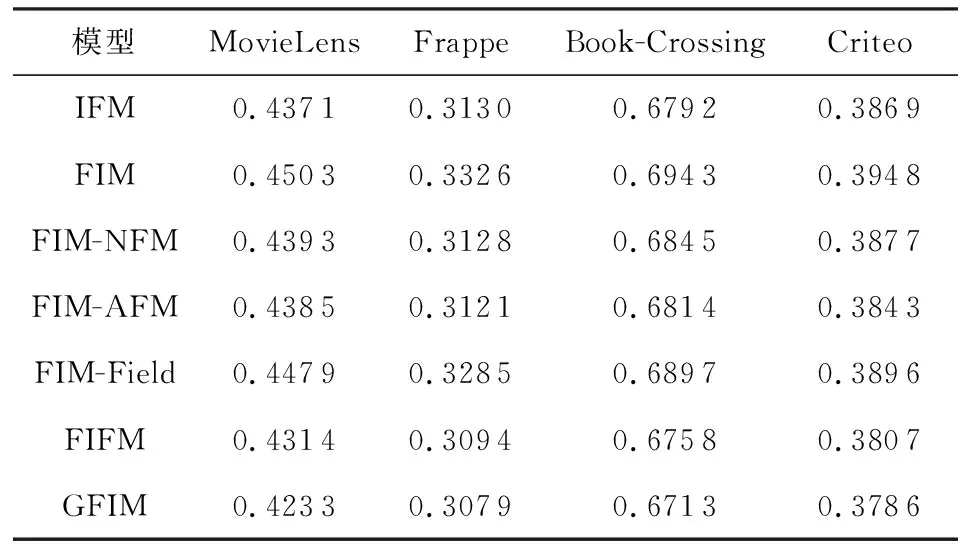
Table 4 Impact of FIM表4 FIM的影响

从表4我们可以分析得到：

1) 单以FIM组件直接作为输出结果，自身就有较好的预测效果，相比于原始的FM，在MovieLens，Frappe，Book-Crossing，Criteo依次提升了3.95%，0.87%，2.66%，5.90%.与此同时，FIM在MovieLens和Book-Crossing数据集上比表3中的FFM提高了1.55%和0.57%，而在MovieLens数据集上比表3中的DeepFM提高了0.28%，验证了FIM自身就能携带较为丰富的预测影响因子(对应3.4节的效果2).

2) FIM在类别较多的数据集上提升效果更为明显.例如FIM在Criteo上甚至高于NFM，并与表3中的AFM结果相接近.我们认为主要原因可能是Criteo数据集拥有多达39个类别，具有丰富的类别信息，相比于NFM和AFM只在特征上进行交互，FIM将特征和类别信息进行了融合，更能发挥在多类别数据集上的优势.

3) 虽然FIM具有一定的预测效果，但其在所有数据集上的表现仍差于IFM，这主要得益于IFM对特征交互和类别交互信息都进行了抽取，也说明了特征交互及类别交互的融合能够很好地支持模型的预测.

4) 为了充分验证FIM在各个模型上的影响力，我们还探究了FIM与第3节提到的NFM，AFM，IFM中的类别组件部分的组合版本.从实验中可以发现，NFM和AFM在集成了FIM组件后在4个数据集上均有不错的提升效果.其中，FIM-NFM在Frappe数据集上甚至高于了IFM，FIM-AFM在Frappe和Criteo上高于了IFM，说明了本文所提出的FIM不仅自身具有不错的预测能力，还能为其他的FM模型带来较好的增益效果(对应3.4节的效果3).

5) 与FFM相比，虽然FIM也使用了类别的概念，但二者的角度完全不同，FFM是为每一个特征都对应一系列存在的类别，初始化的计算模型是一个关于m，n，d的3维张量，而FIM在计算类别时默认非0特征属于一个类别，计算模型是一个关于n和d的2维矩阵，能极大地节省参数空间.

6) 从上述1)～5)分析得出，所提出的FIM不仅能和各类FM变体无缝衔接，还能为这些FM模型带来不错的增益效果，甚至在无任何模型下也可以超越原始的FM模型，证明了FIM的有效性.

实验3.不同模型的时间消耗.

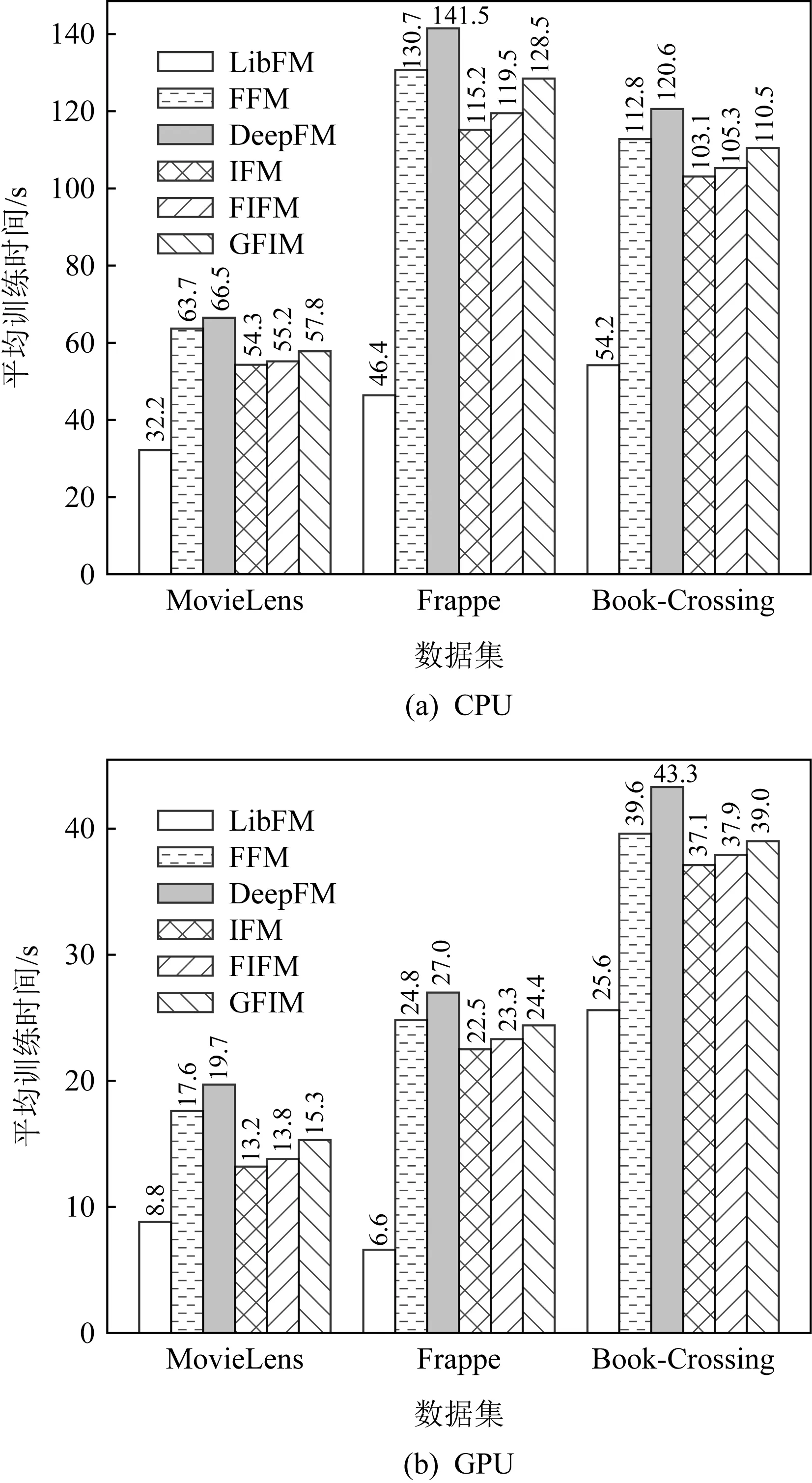
Fig. 6 Average training time of each epoch for different models on CPU and GPU图6 在CPU和GPU上模型每轮的平均训练时间

为了进一步验证参数量对于模型训练在时间上带来的影响，我们统计并计算不同模型在CPU和GPU上40轮的平均每轮训练时间.为方便直观展示，我们选取了4个有代表性的模型进行对比：LibFM，FFM，DeepFM，IFM.其中FIFM和GFIM参数量要多于LibFM和IFM，并且小于FFM和DeepFM.实验结果如图6所示:

从图6中我们可以发现：

1) 所有模型在GPU的训练时间要明显少于CPU，这主要得益于GPU可以在执行深度学习任务时使用更多的核心进行并发计算，也是当前主流服务器都采取GPU进行深度学习的主要原因[13].

2) 虽然FFM在参数上要远多于其他模型，但训练时间并未表现出与参数量成正比例的关系，相比DeepFM，FFM的训练时间甚至还要略短一些，这可能是因为FFM在训练时只做了通用的2阶交互，参数量的增加虽然为其带来了一定的计算复杂度，但相比于DeepFM复杂的多层感知机网络计算过程，计算时间花销更小，因此时间消耗也能保持在可接受的范围.

3) 得益于FM简化型的结构，LibFM在CPU和GPU上都有最快的训练速度，但带来的不足是交互时学习到的信息量不足，导致它在所有的数据集上的表现最差.

4) 由于FIFM可看作是在IFM的基础上增加了FIM模块，因此在训练时间上要略长于当前最好的IFM.从图6中CPU实验结果可以看到，增加FIM后在时间上带来的每轮花销在CPU上只体现在1～4 s之间，对于在40轮迭代之前就到达收敛的模型来说也是能够接受的.此外，得益于GPU的加速能力，FIFM模型的训练时间在GPU上相比于IFM可以缩短到平均不足1 s，这对于当下GPU作为主流深度学习服务器的场景是完全可以忽略的(对应3.4节的效果4的时间消耗).

5) GFIM作为FIFM的神经网络版本，由于加入更为高阶的多层感知机，训练时间长于FIFM，但由于GFIM在主体结构上传承于FIFM，因此它的总体时间也相较FFM和DeepFM有所降低.

6) 从上述1)～5)分析可知，FIFM和GFIM在实际训练时是完全能够满足当下服务器对于时间复杂度的需求.

实验4.不同策略在数据集上带来的影响.

为了进一步验证组成FIFM模型的各个策略在训练的过程中对最终的表现结果带来了哪些影响.我们做了对比实验:将Fea(+)记为仅保留特征交互的方法，线性部分保持不变.将Field(+)记为仅保留类别交互的方法，而将Fea_Field(-)记为FIFM去除特征-类别权重后(保留特征交互和类别交互)的方法.将Fea(+)、Field(+)、Fea_Field(-)这3个方法结合已有的FIFM模型在2个训练集上进行了40次迭代训练，并记录下它们在测试集上每一轮的表现.

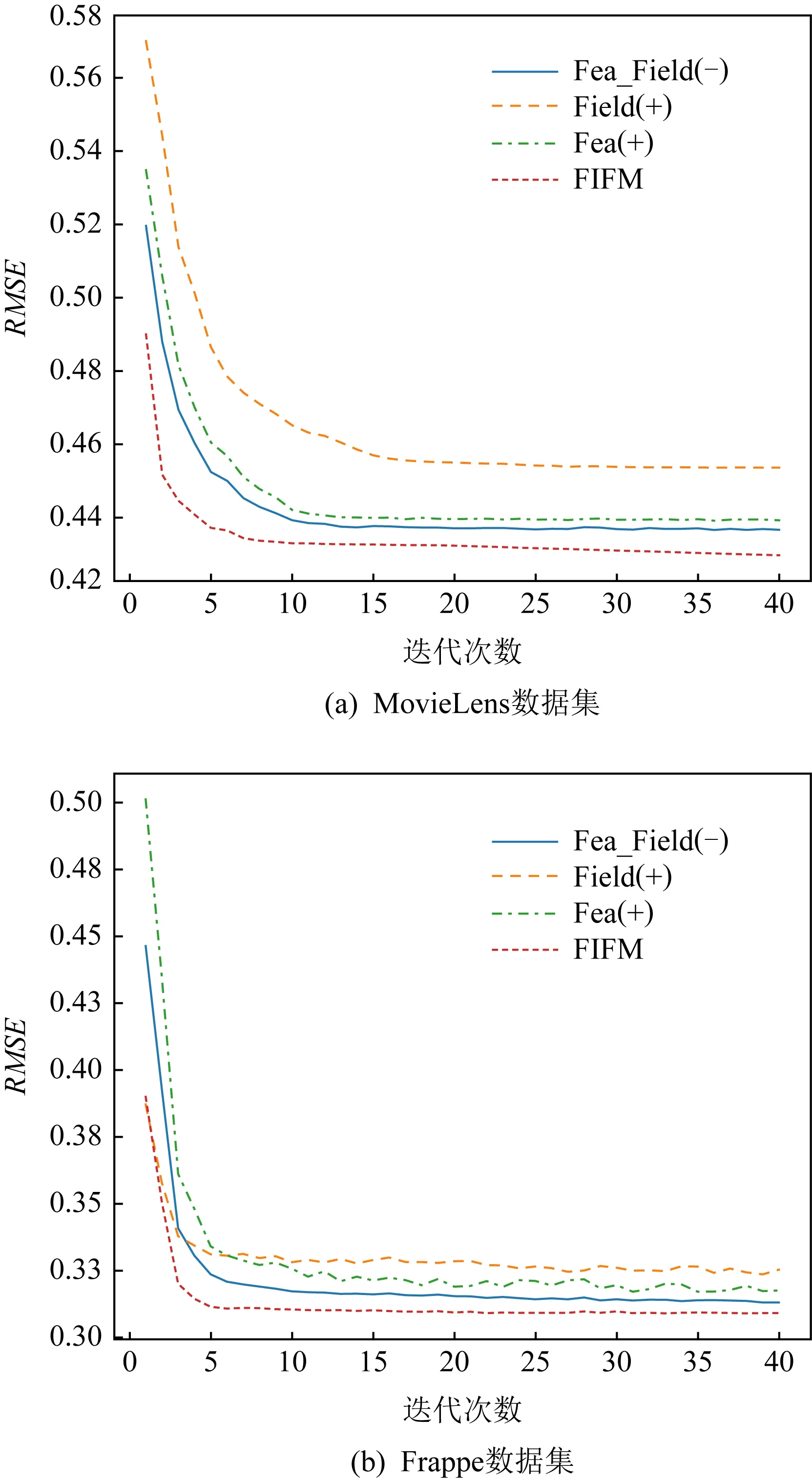
Fig. 7 Performance of different strategies on MovieLens and Frappe datasets图7 不同策略在MovieLens和Frappe数据集上的表现

图7展示了不同策略在MovieLens数据集和Frappe数据集上的表现.可以看出，随着迭代次数的增加，所有的模型都逐渐趋向于收敛.毫无疑问的是，集合了所有策略的FIFM获得了最好的效果.对于收敛速度而言，在MovieLens和Frappe数据集上获得最快收敛的分别是FIFM和Field(+).在模型趋于稳定后，不同策略的表现结果从大到小依次为FIFM>Fea_Field(-)>Fea(+)>Field(+).我们可以发现，结合了特征嵌入矩阵和类别嵌入矩阵的Fea_Field(-)比单独的交互学习具有更明显的提升作用.此外，特征交互带来的增益大于类别交互，这也是由于特征向量包含了类别向量不具备的更为精细化的信息.相比MovieLens,Field(+)在Frappe上收敛得更快，这可能是因为Frappe的类别特征具有10个，相比MovieLens的3个，类别嵌入矩阵可以得到更充分的学习.

实验5.不同维度的模型在数据集上的效果.

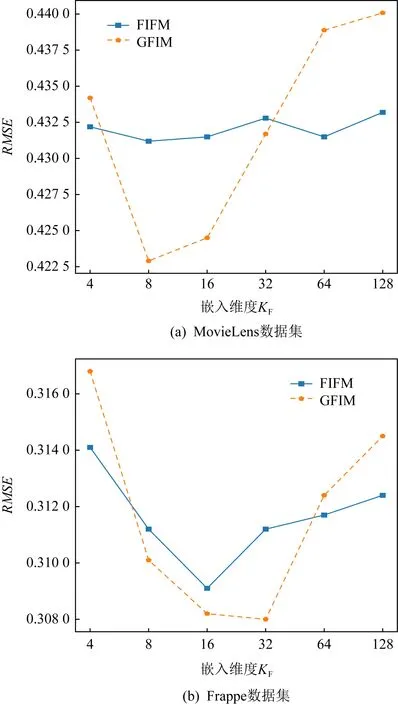
Fig. 8 Performance of varying field embedding KF on MovieLens and Frappe图8 不同类别嵌入维度KF在MovieLens和Frappe上的表现

我们比较了不同的类别嵌入维度KF在2个数据集上的表现.从图8中看到，随着维度的持续上升，表现效果也会因过拟合而有所下降,因此合理的KF值需要取决于不同数据集具体的数据特征.例如图8(a)中，KF在MovieLens上获得最佳表现的嵌入维度8要明显区别于图8(b)的嵌入维度32.我们也将其归结为数据集的类别因素.由于Frappe上的类别数10要远多于MovieLens上的3，因此感知交互层能够获取9×10/2=45个交互向量，而同样的MovieLens只能获取2×3/2=3个交互向量，故获取可训练信息也就远小于Frappe，导致更小的维度提前达到了训练的饱和状态.同时，我们注意到，FIFM随着维度变化的波动性要小于GFIM，这是由于GFIM引入了逐点相乘的向量级别乘法，对维度变化更为敏感.但相比于特征-类别标量计算的FIFM也容易取得最佳效果，同时也更容易带来过拟合问题致使后续效果下降.

图9展现了特征嵌入向量的维度d在MovieLens和Frappe上的表现.不同于类别嵌入矩阵维度KF，特征嵌入矩阵维度d需要更大的数值以获得最佳的表现效果.FIFM和GFIM在2个数据集上的最佳取值均在256左右，此维度要远远大于KF的8和32，间接说明了特征交互相比于类别交互具有更丰富的信息量，这也是此前众多基于特征交互的FM改进模型获得成功的原因.而GFIM受到过拟合的影响带来的RMSE表现下降也没有图8中的类别交互那么明显.

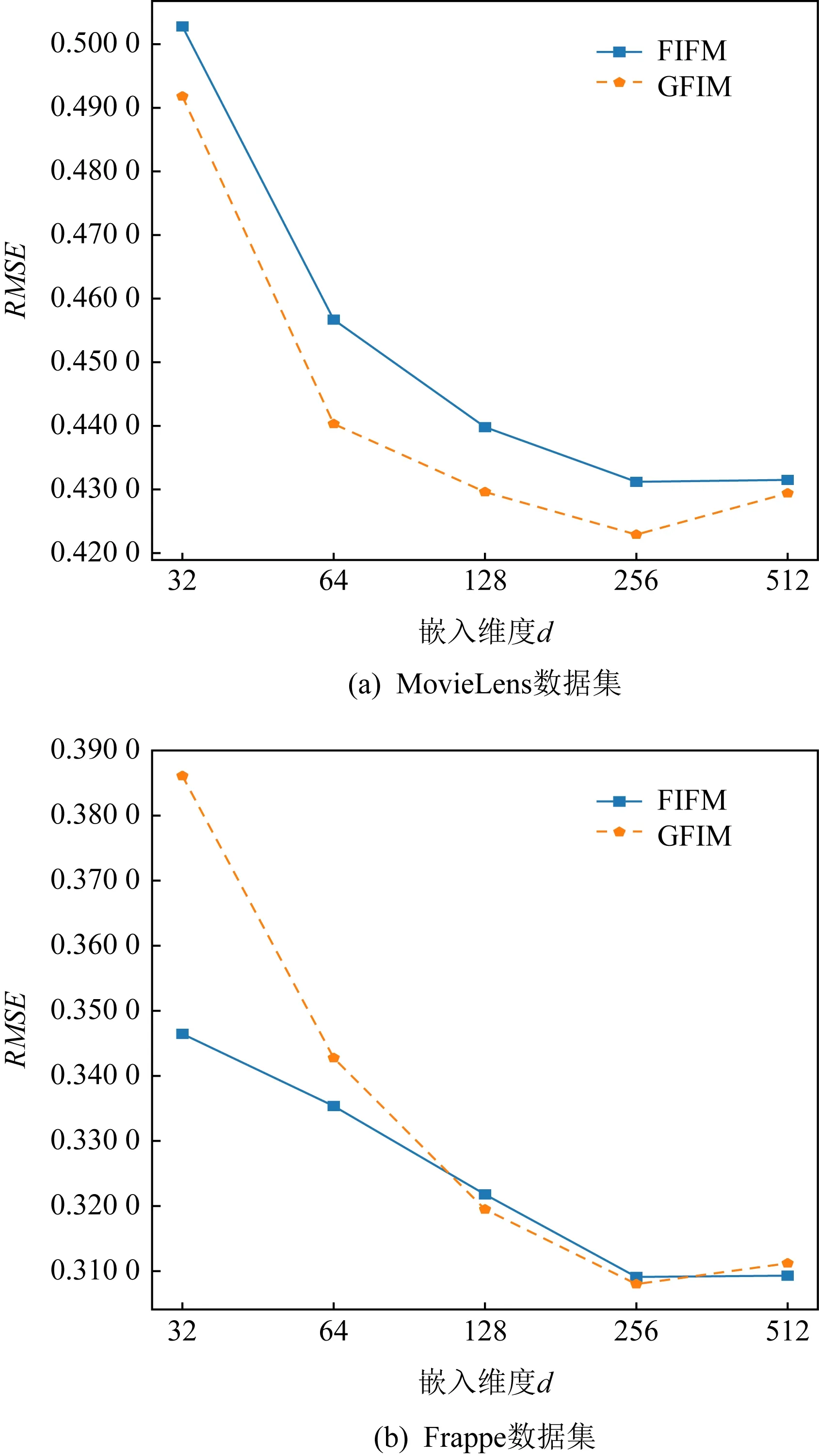
Fig. 9 Performance of varying feature embedding don MovieLens and Frappe图9 不同特征嵌入维度d在MovieLens和Frappe上的表现

相比于其他稀疏预测模型，本文提出的FIFM具有更好的表现效果.GFIM在FIFM基础上引入了神经网络作为支撑，从而进一步提升了实验效果的上限.

实验6.数据稀疏环境下不同模型的性能比较

为了进一步评估数据稀疏性对推荐性能的影响，我们在MovieLens上选取不同规模的数据内容,用于模拟不同稀疏程度(10%,30%,50%,70%,90%)的训练数据集，所有模型在不同程度数据稀疏环境下的性能表现如表5所示:

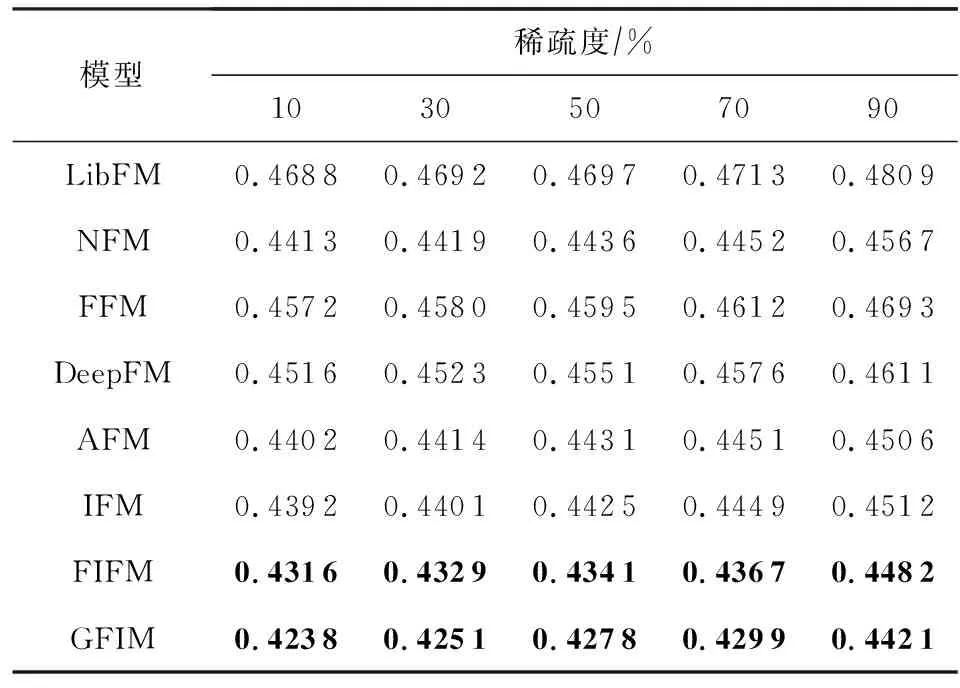
Table 5 RMSE Comparison of All Models with Different Sparse Degrees on MovieLens

从表5中我们可以发现，伴随着MovieLens数据集稀疏程度的上升，所有的模型表现效果均有不同程度的降低.需要特别指出的是，在90%稀疏条件下，所有模型均有较大幅度的性能下降.而基于FM的改进模型例如AFM或DeepFM，由于采用了神经注意力机制或深度高阶特征拟合学习方法，下降幅度小于原始的FM.同时我们还发现，FFM和IFM均引入了类别交互模型，但FFM的表现整体上要差于依赖于神经网络机制的IFM，也差于未考虑交互模型的DeepFM，这表明了深度学习在特征拟合时仍然具有强大的高阶特征拟合能力.

5 总 结

本文从特征-类别融合的角度出发，提出了一种新的特征-类别交互因子分解机模型(FIFM)，并基于深度学习的泛化理论给出了相应的神经网络扩展模型GFIM.相比于从特征交互角度出发的FM,NFM,AFM，从类别交互角度出发的FFM和以特征、类别分别交互角度出发的IFM模型，我们提出的模型加入了从特征-类别融合的视角，并设计了一种新的特征-类别融合交互机制(FIM).FIM计算特征和类别融合后的交互特征，丰富了在各类稀疏场景下的高阶语义信息和潜在预测因子，进一步提高了预测的准确性.同时，本文还进行了多类实验来探究在不同场景下的预测结果，记录了不同数据集下的时间和空间消耗情况，并分析了原因.在4个真实数据集上的实验结果表明，在常规实验环境和稀疏实验环境下，本文提出的FIFM和GFIM模型相比于主流的预测模型在RMSE指标上都具有提升效果.

作者贡献声明：黄若然负责论文框架设计、算法提出、实验设计和运行，以及论文撰写、修订和最终审核;崔莉负责论文整体研究思路的提出、内容设计和最终版本修订;韩传奇负责部分内容撰写、文献调研以及插图设计和修订.