再解数学问题

张孟娟

● 学习内容分析

本课节选自2019年教科版《必修1 数据与计算》4.2《数值计算》，主要内容为“绘制数学函数曲线”和“求解斐波那契数列”两个任务。本课的主要意图旨在帮助学生掌握数值类问题求解常用的算法思想，针对问题来选择合理的算法以解决实际问题。考虑到两个任务属于并列关系，且任务之间关联度不高，没有紧密联系实际问题的求解，只停留于数值计算的知识层面，所以本课通过求解折纸折痕数量的两种方法来串联两个任务包含的主要知识点，让学生通过自主探究、小组合作等活动，更深入地理解算法、学习算法，引导学生体验运用程序解决问题的过程。

● 学习者分析

本课的学习对象为高一年级的学生，他们已经具备较高的抽象逻辑思维、分析能力与辩证思维。在知识层面上，他们已经初步掌握了Python的变量赋值、选择、循环等基本结构，学会了利用自然语言和流程图描述解决问题的算法，具备了一定的编程能力，并且好奇心较强，喜欢通过实践探究来解决问题。在发展需求层面，他们虽然已经学习了Python编程中的基本概念与结构，但囿于实践经验匮乏，在程序的整体编写方面还存在困难，程序设计思想的基础比较薄弱。学生通过本课的学习，可以进一步增强自身利用编程解决问题的意识，提高发现、分析、解决问题的能力。

● 学习目标

信息意识：针对折痕数量计算这一问题，进行需求分析，综合判断信息，选择合适的方法解决问题。

计算思维：①通过绘制指数函数图像，能够明确Python利用numpy和matplotlib两个模块绘制图像的基本方法，感受数据的图形化表示;②通过求解折纸折痕数量，掌握数值类算法在实际问题解决过程中的应用及常用方法，能够使用解析式或迭代方程，进行数值计算、解决实际问题，并能够迁移到其他问题的解决过程中。

数字化学习与创新：能够利用Python工具设计与完善程序，养成数字化学习与创新的习惯。

● 教学重难点

重点：①numpy和matplotlib两个模块绘制函数图像的方法;②数值类算法在实际问题解决过程中的常用方法，如迭代法。

难点：迭代算法解决问题的关键步骤，利用迭代法求解折痕数量。

● 教学过程

1.创设情境，提出问题

呈现问题情境：折纸中包含许多数学问题，如折纸厚度计算问题、折痕数量问题等，今天我们将一起探究有关折纸折痕数量的问题。一张A4纸，如果对折一次，会得到一条折痕;如果继续沿着一个方向对折，让每次折痕都与上次折痕保持平行，会得到3条折痕;如果再对折，折痕数量也随之增大。对折n次后，纸上会有几条折痕？

设计意图：以求解折纸折痕数量的趣味数学问题作为导入，激发学生的探究兴趣。

2.循序渐进，分析问题

活动一：两人一组，讨论折痕数量与对折次数之间的规律，思考第n次对折对应的折痕数量是多少？

讲解：①总结规律为2n-1，引出两者之间的关系式是指数函数;②指出用图像表示数学函数的意义。

提问：生活中绘制图像的软件有很多，你们可以想到哪些？

讲解：①总结学生的回答内容，展示使用Excel绘制y=2x-1函数图像所出现的问题——关键点不足，精度不够;②指出利用程序描点，可以达到速度快且精确度高的效果，引出使用Python绘制函数图像。

设计意图：引导学生通过比较分析，明白解决问题的需求，为后面选择解决问题的合适算法打下基础。

3.学练结合，解决问题

讲解：①numpy模块常用函数及相关语句用法——arange（）可以创建等差数列，是绘制更多点对，使图像更加光滑的关键;numpy模块加载以及arange（）函数语句的编写。②matplotlib模块常用函数及相关语句用法。③总结Python模块调用的一般步骤：安装相关模块—加载模块—调用语句—完善及运行程序。

活动二：根据部分参考代码（如图1）和示例图（如图2），用Python绘制指数函数y=2x-1，1≤x≤10的图像。

活动2参考答案：①y=（2**x）-1;②plt.title（‘y=（2**x ）-1’）;③plt.xlabel（'X'）;④plt.ylabel（'Y'）。

设计意图：让学生在动手实践的过程中加深对所学知识的理解，感受程序创作的魅力及数字化工具的优势。

4.深入思考，分析问题

提问：除了用2n-1（n>=1）表示折痕數量，想一想还可以怎么表示？

讲解：①总结折痕数量与对折次数之间的另一种关系表达式：f（n）=2f（n-1）+1（n>=2）;②结合上述关系式讲解迭代过程。

设计意图：针对同一个问题，鼓励学生思考解决问题的不同方法，培养学生的逻辑思维和发散思维。

5.层层深入，解决问题

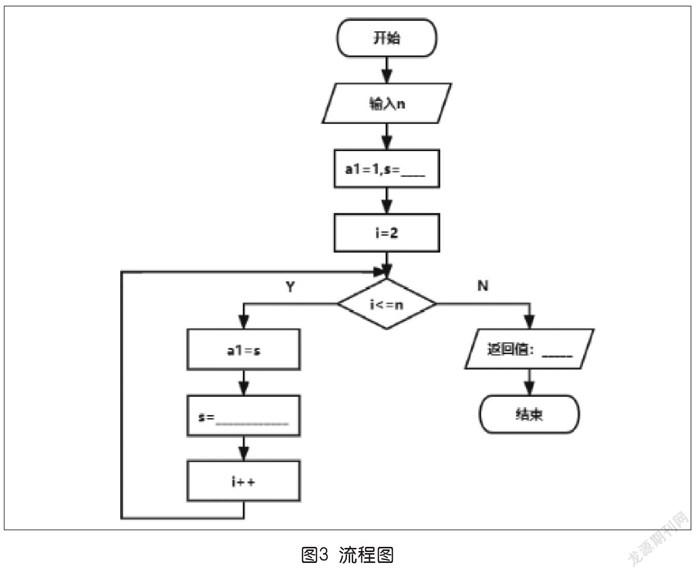
活动三：补全导学案中的流程图（如图3），并尝试利用迭代思想，编写Python程序。（功能要求：输入第n次对折，计算对应的折痕数量）

讲解：①依据流程图梳理算法设计的过程;②函数调用的相关语句。

小结：迭代算法的三个关键步骤：确定迭代变量——建立迭代关系式——对迭代过程进行控制。

设计意图：从补全流程图到代码编写，帮助学生明确算法设计的流程，奠定学生编写程序的基础。活动从易到难，层层深入，能够帮助学生消除畏难情绪，更好地理解迭代算法解决问题的关键步骤。

6.拓展练习，巩固知识

活动四：补充代码，完成程序（如图4）。将答案上传至UMU学习平台。

参考答案：第1题：①-50;②51;③x*x-2*x+1;④plt.plot（x，y）。第2题：①n+1;②f1，f2=f2，f1+f2;③f2。

设计意图：通过拓展练习，促进知识迁移;同时借助UMU平台，实时查看学生的作答情况，针对性讲解学生的疑惑问题。

7.梳理知识，形成评价

进行课堂小结，组织学生根据UMU学习平台上的评价问卷，进行自我评价，并填写本节课的收获与疑问。

设计意图：通过课堂小结及自我评价，帮助学生回顾知识、总结收获，引导学生在生活中积极利用计算机解决实际问题。

● 教学反思

本节课采用“提出问题—分析问题—讲解新知—解决问题—巩固总结”的教学过程，以问题串联的方式层层递进、由浅入深地促使学生通过讨论、比较等方式逐步构建新知识、新技能，注重培养学生的学科核心素养。

从单元设置的意图来看，本单元注重探究“计算”，更多关注的是问题解决的过程，即描述和变换信息的过程。因此在教学过程中，本节课以“折纸中的趣味数学问题”作为活动主线，注重培养学生界定问题、抽象特征、形成与迁移问题解决方案的思维能力。首先，通过折纸中的折痕数量问题引入新课，激发学生探究兴趣，培养学生的信息意识;其次，通过求解折痕数量的两种不同方法，串联了函数图像绘制和迭代算法两节内容，在学生通过编程实现两种不同算法的过程中，注重借助自然语言和流程图帮助学生理解知识，发展学生的计算思维;最后通过拓展练习以及总结评价，促进学生知识迁移、融会贯通，引导学生在生活中进行积极思考，养成利用数字化工具解决问题的习惯。由于教材设置的两个任务属于并列关系，所含内容较多，本节课虽有意识地串联两个任务所含知识，但受课时限制，在实际教学中，节奏相对较快，对于一些知识的归纳总结有所欠缺，如图像化表达的意义、用计算机解决问题的一般过程等。