基于高稳定性的PGC解调算法研究

王 梦，孔 勇，吴 虎，李 欢，王春阳

(上海工程技术大学 电子电气工程学院 电子信息系, 上海 201620)

引 言

光纤干涉传感器因其高灵敏度、低成本和抗电磁干扰的优点而成为最有前途的技术之一[1-3]。它们在磁场检测、水听器、输油管道泄漏测试和应变监测领域有很好的应用[4-7]。传统的相位解调技术主要包括有源零差[8]、无源零差常采用3×3耦合器[9]、外差法[10]和相位生成载波(phase generated carrier,PGC)解调技术。为了恢复干涉型光纤传感器的相位变化，通常采用PGC离散余弦变换(discrete cosine transform，PGC-DCM)[11]和PGC反正切(PGC-arctan)[12]解调算法。然而，传统的PGC离散余弦变换解调算法会受光强扰动的影响导致解调结果恶化[13]。PGC反正切解调算法虽然可以消除光强扰动的影响，但是它的解调效果却依赖于调制深度，当调制深度C偏离2.63rad时，解调结果会受到严重的谐波干扰导致信号失真[14]。

为了解决这些问题，2010年，HE等人[15]为了消除光强扰动的相关参量，提出了一种PGC反正切微分自乘算法(differential self multiplication,PGC-arctan-DSM)，与DCM算法相比，稳定性大大提高，但是其运算较为复杂。2012年，WANG等人[16]提出了一种PGC-DSM解调算法，以消除光强干扰，降低谐波失真，但解调过程过于复杂，而且实时性较差。2014 年，ZHANG 等人[17]提出了新的解调算法，将基频混频进行改进，并且在系统中加入直流滤波器来消除信号的直流分量对解调结果的影响。2015年，ZHANG等人提出了使用参考补偿的PGC解调算法来抑制光强扰动(light intensity disturbance，LID)[18]，然而，它需要在干涉仪的一个臂上添加具有压电换能器的参考信号，因此不利于器件小型化。2018年，SUN等人[19]提出了一种改进的相位生成载波解调算法，通过信号混频运算，能够在小信号范围内改善直流分量对系统的影响，然而解调效果仍会依赖于调制深度。

本文中提出了一种新的改进的相位生成载波解调算法，将输入信号进行微分交叉相乘、相除、积分等运算。通过仿真验证，该算法可以消除光强扰动和调制深度对传感器的影响，在性能上也优于WANG等人[20]提出的基于PGC微分自乘和反余切函数(PGC-arccot-DSM)解调算法。

1 原 理

1.1 PGC调制原理

为了有效地获取干涉型光纤传感器上的干扰，采用PGC解调技术的传感系统需要引入载波调制信号，载波调制信号可以采用内调制或外调制的方法。内调制是对激光器的波长进行调节从而实现对信号的调制，此方法不需要将载波信号引入到调制器上。外调制是通过把载波信号加到压电陶瓷环(piezoelectric transducer，PZT)原件上，在其驱动下产生伸缩效应，从而使干涉仪一臂上的光纤的长度、折射率发生改变，导致光波相位差随着载波信号的波动而发生变化，最终达到相位调制。图1显示的是外调制型迈克尔逊干涉传感器系统，其中LD为半导体激光器(laser diode)，C1、C2为耦合器，PD为光电探测器(photodetector)。

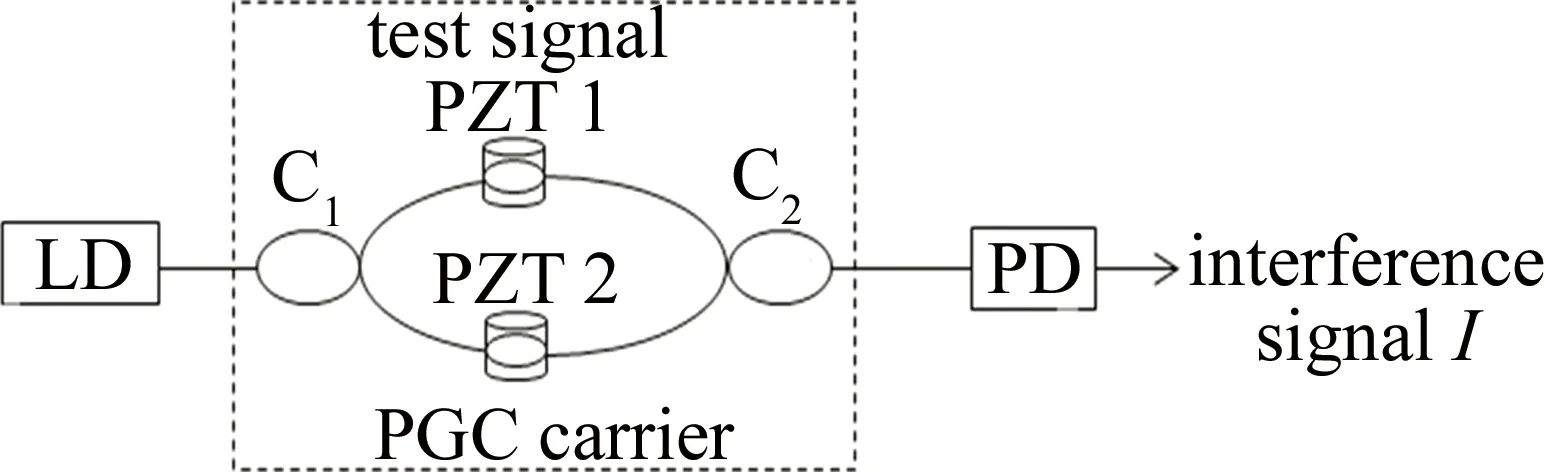
Fig.1 Basic structure of external modulation Mach-Zehnder interference optical fiber sensor

上述结构中，通过光电探测器输出的干涉信号可以表示为：

I=A+Vcos[Ccos(ω0t)+φ(t)]

(1)

式中，Ccos(ω0t)是载波信号引起的相移，t是时间，φ(t)是包括原始相位差和低频环境噪声引起的相移，C是载波信号的调制深度，ω0是载波信号的频率，V是交流分量，V=mA，(m≤1)，其中m是干涉条纹的可见度，A是光强。在表达式Ccos(ω0t)+φ(t)中，载波频率ω0必须远大于待测信号φ(t)的频率，因此可以认为载波信号携带感测信号。将(1)式以k阶贝塞尔函数J(·)展开可得到：

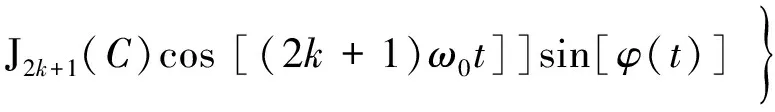
(2)

1.2 PGC解调原理

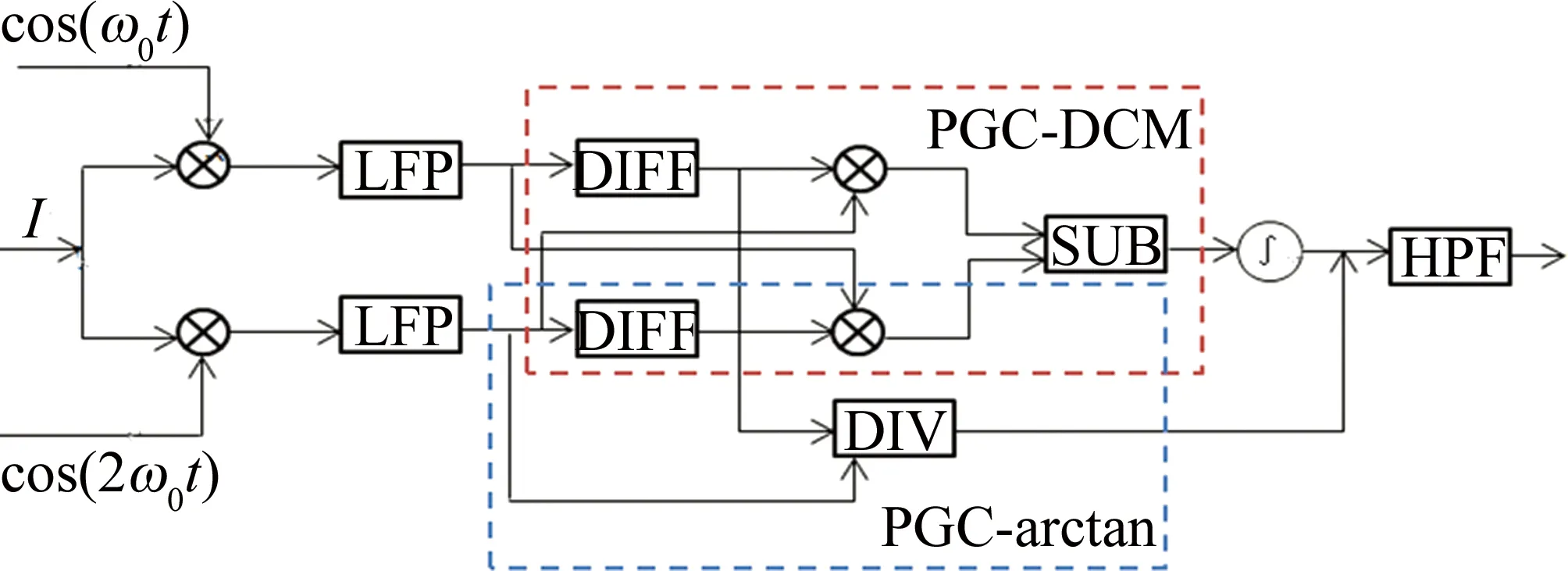
Fig.2 Principle block diagram of the traditional algorithm

由图2可知，干扰信号分别与基波载波和二次谐波载波混频相乘，高频被两个低通滤波器滤除后，得到一对正交分量L1(t)和L2(t)：

L1(t)=-AVJ1(C)sin [φ(t)]

(3)

L2(t)=-AVJ2(C)cos[φ(t)]

(4)

式中，J1(C)和J2(C)分别是1阶和2阶的贝塞尔函数展开式，PGC-DCM算法中，基于离散余，最终通过高通滤波器输出的信号为：

Y(t)=(AV)2J1(C)J2(C)φ(t)

(5)

由(5)式可知,如果(AV)2J1(C)J2(C)是一个常数，则相位信号可以由(5)式线性解调。因此解调输出的容差取决于J1(C)J2(C)如何随C的值和A,V的稳定性而变化。如果A,V和C随环境温度等因素变化，输出信号会产生一定的误差。参量A,V取决于干涉信号的光强和可见度，并且分束器和激光源输出的任何变化或光纤干涉仪(fiber optic ring interferometric，FOI)臂中的偏振变化都可能引起V的波动。而在PGC-arctan算法中，两路信号经过微分运算后，只需要进行相除，再通过高通滤波器，最终得到的输出信号为：

(6)

由(6)式可以看出，该方法的解调结果受调制深度C影响，理想情况下，需要将C值调整到2.63rad才能使J1(C)=J2(C)，然后通过反正切就能把φ(t)解调出来，但是调制深度C通常易受环境的影响发生漂移从而导致解调失真，所以克服C值的影响也是一个需要深入研究的内容。

2 PGC改进算法原理

为了克服光强扰动对传统算法的影响，以及传统算法对调制深度的依赖，提出了一种改进的PGC解调算法，其解调原理框图如图3所示。

Fig.3 Principle block diagram of the improved algorithm

将(3)式、(4)式进行微分自乘，分别得到X1(t)和X2(t)：

(7)

(8)

将(7)式与(8)式相除得：

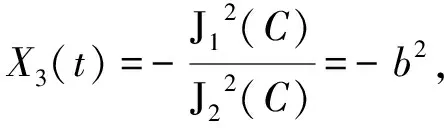
(9)

式中，n为替换参量。然后将基波载波信号的一路微分信号和(4)式相乘得到S1(t)，(4)式自乘平方得到S2(t)：

S1(t)=(AV)2J1(C)J2(C)sin[φ(t)]×

(10)

S2(t)=(AV)2J22(C)cos2[φ(t)]

(11)

将(10)式与(11)式相除得S3(t)：

(12)

由(12)式看出，信号中只含有带贝塞尔常数和一个待测信号的乘积形式，此时只需要将(9)式代入相除再进行积分便可以成功解调出待测信号φ(t),最后通过一个高通滤波器来消除系统中含有低频信号的噪声。由原理分析可知，改进的解调算法中成功消除了光强扰动参量A和V，以及对调制深度C的依赖性。为了验证上述的原理分析，以下通过LabVIEW进行仿真实验验证。

3 仿真结果分析

3.1 光强扰动下的稳定性分析

为了验证改进PGC解调算法在抑制光强扰动方面的优势，比较了改进PGC解调算法和PGC-DCM算法的性能。干扰信号和测试信号分别设置500Hz和700Hz的频率，载波的频率设置为50kHz，LID的深度设置为0.5。模拟的解调结果分别如图4a和图4b所示。

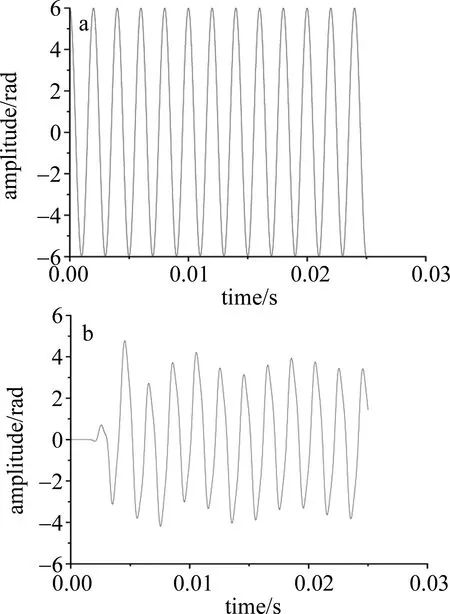
Fig.4 Results under different algorithmsa—PGC-improved algorithm b—PGC-DCM

由图4可以看出，当系统中引入光强扰动时，传统的PGC-DCM会因此出现信号失真，这是由于在实际中光源输出不稳定或光在光纤中传输发生偏振衰落而导致的现象，而改进的PGC算法能有很好的解调效果。为了更好地说明改进算法能够改善光强扰动所带来的稳定性影响，改变扰动幅度从1.5rad调制到3.5rad，并且通过计算其信纳比(signal-to-noise and distortion ratio，SINAD)来评估它们的解调性能，结果如图5所示。改进PGC算法的SINAD平均高于25dB，比PGC-DCM算法高出近15dB，可以看到，改进PGC解调算法的性能优于PGC-DCM算法，而且具有更高的信纳比，能够很好地抑制LID的影响。

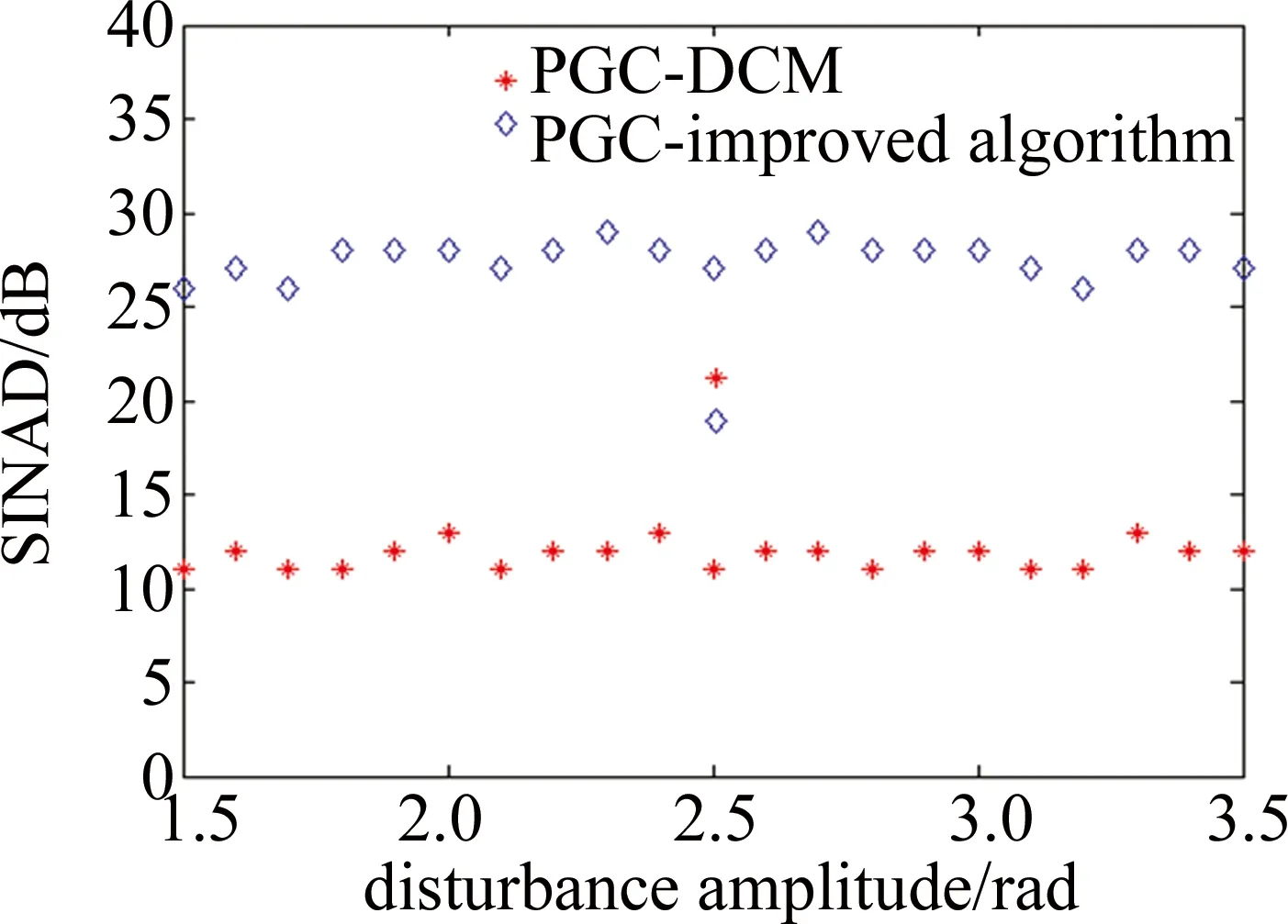
Fig.5 SINAD of PGC demodulation algorithm under different disturbance amplitude

3.2 调制深度对解调性能的影响

众所周知，当调制深度偏离2.63rad时，在PGC-arctan算法中引入了很大的谐波失真。为了说明改进的PGC算法优于PGC-arctan算法并且不受调制深度C的影响，将调制深度值设置为2.5rad，测试信号频率设置为800Hz，扰动幅度为2rad，仿真解调效果如图6所示。可以发现，当调制深度偏离理想值时，传统算法都出现了解调失真的现象，而基于改进的算法明显不依赖于C值的变化，依然能够很好地解调出信号。图6d为WANG等人提出的PGC-arccot-DSM的解调结果，同样是去C值的改进算法，本文中提出的算法在解调效果上明显优于该算法。为了更好地说明改进算法不再依赖于调制深度的变化，现将调制深度C从1.5rad变化到3.5rad，通过LabVIEW仿真得出它的信纳比和总谐波失真(total harmonic distortion,THD)来评估它的解调性能，仿真结果如图7、图8所示。

图7和图8中分别给出了3种PGC算法在不同调制深度值下测量的信纳比和总谐波失真，调制深度范围从1.5rad变化到3.5rad。由图中可知，在PGC-arctan算法中，SINAD和THD是对C值相当敏感，当C=2.63rad时，总谐波失真最小至0.0941%，最大信纳比可达到28.01dB。理论上由(6)式可知，当C=2.63rad时，J1(C)=J2(C)，总谐波失真应该为零，并且预期不存在谐波失真，因此，实验中剩余的总谐波失真可能来自原始测试信号的谐波、环境中的噪声和其它谐波失真机制，如频谱重叠和低通滤波器的非理想性能。当C值偏离2.63rad时，解调结果明显恶化，总谐波失真上升，信纳比急剧下降。相比之下，通过具有1.5rad～3.5rad宽范围值的改进PGC解调算法中，可以实现低于0.1%的稳定的总谐波失真和30dB的高信纳比。此外，改进PGC算法实现了比PGC-DCM算法高10dB的信纳比，比PGC-arccot-DSM算法高5dB的信纳比,一个可能的原因是:图3所示改进PGC算法中的除法可以减少由本实验中采用的数字低通滤波器的非理想性能引起的非线性[21]。进一步仿真实验表明，改进PGC解调算法具有较好的系统性能，50Hz时的动态范围为115dB，解调结果和测试信号之间的线性度高达99.99%，如图9、图10所示。

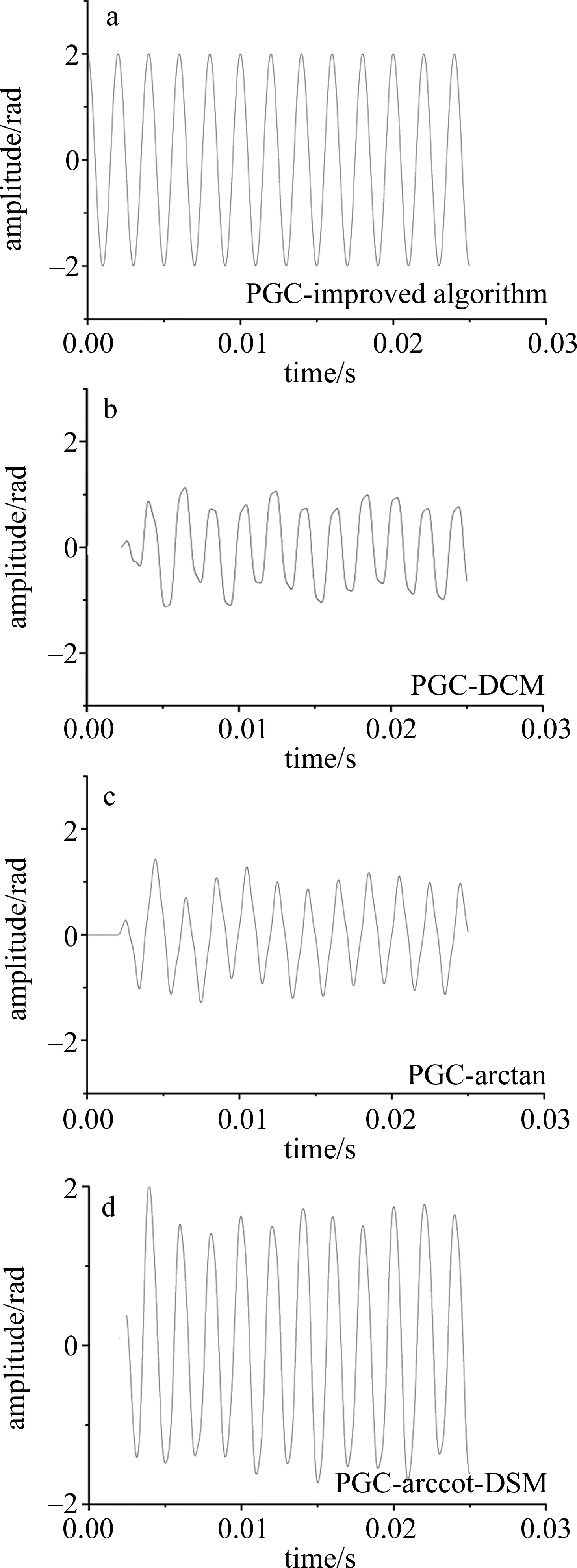
Fig.6 Demodulation results of different algorithms

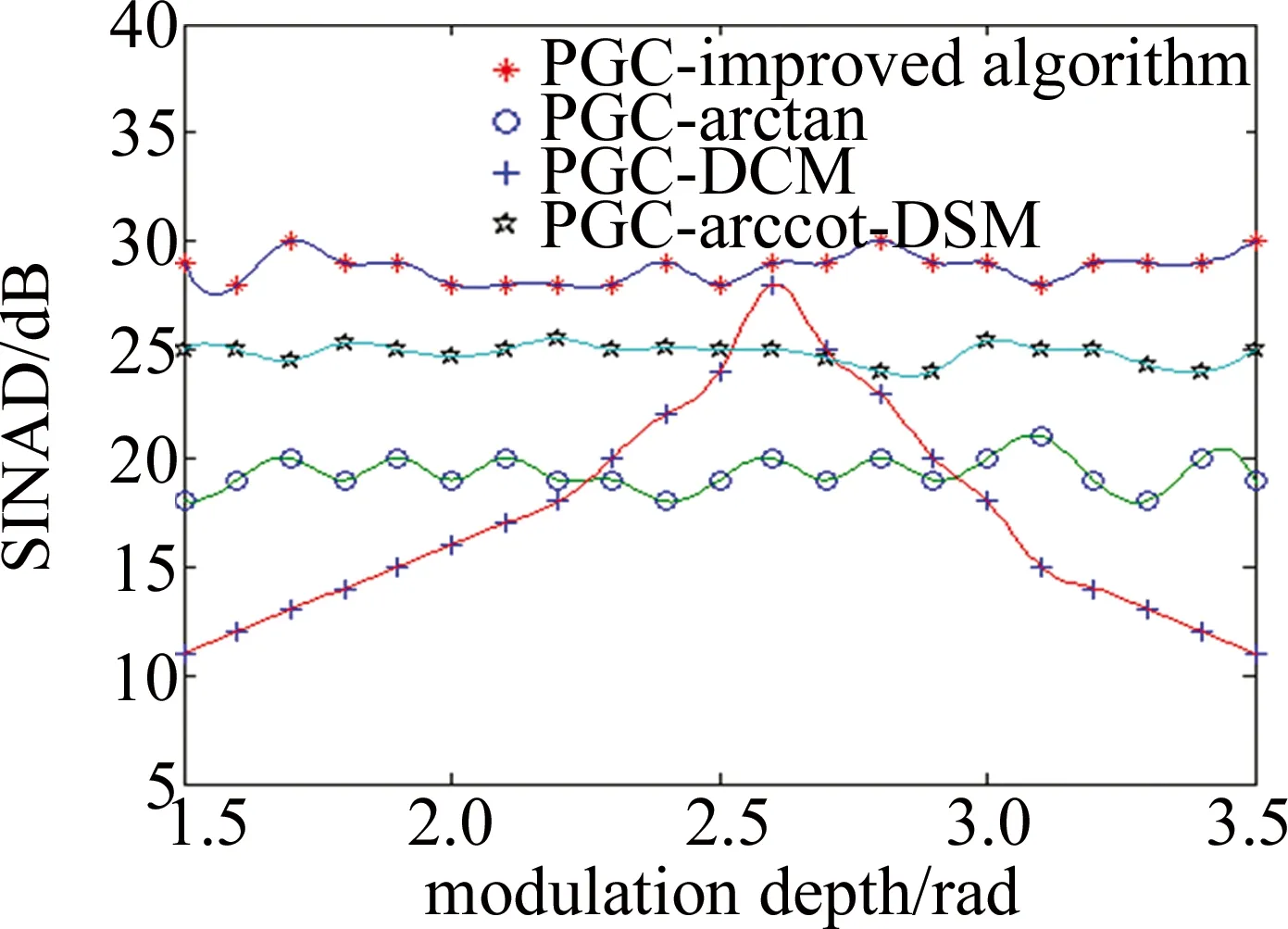
Fig.7 SINAD of PGC demodulation algorithm under different C values

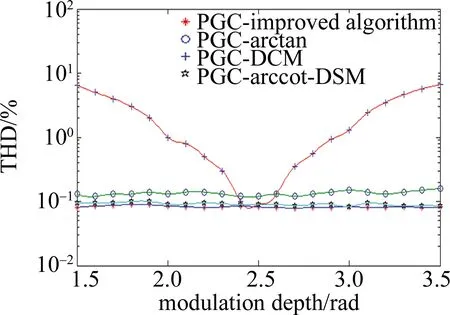
Fig.8 THD of PGC demodulation algorithm under different C values

根据以上分析，得出表1中几种PGC算法的比较，表中显示基于改进的算法具有较高的稳定性和较低的谐波失真,且与相位载波调制深度无关。

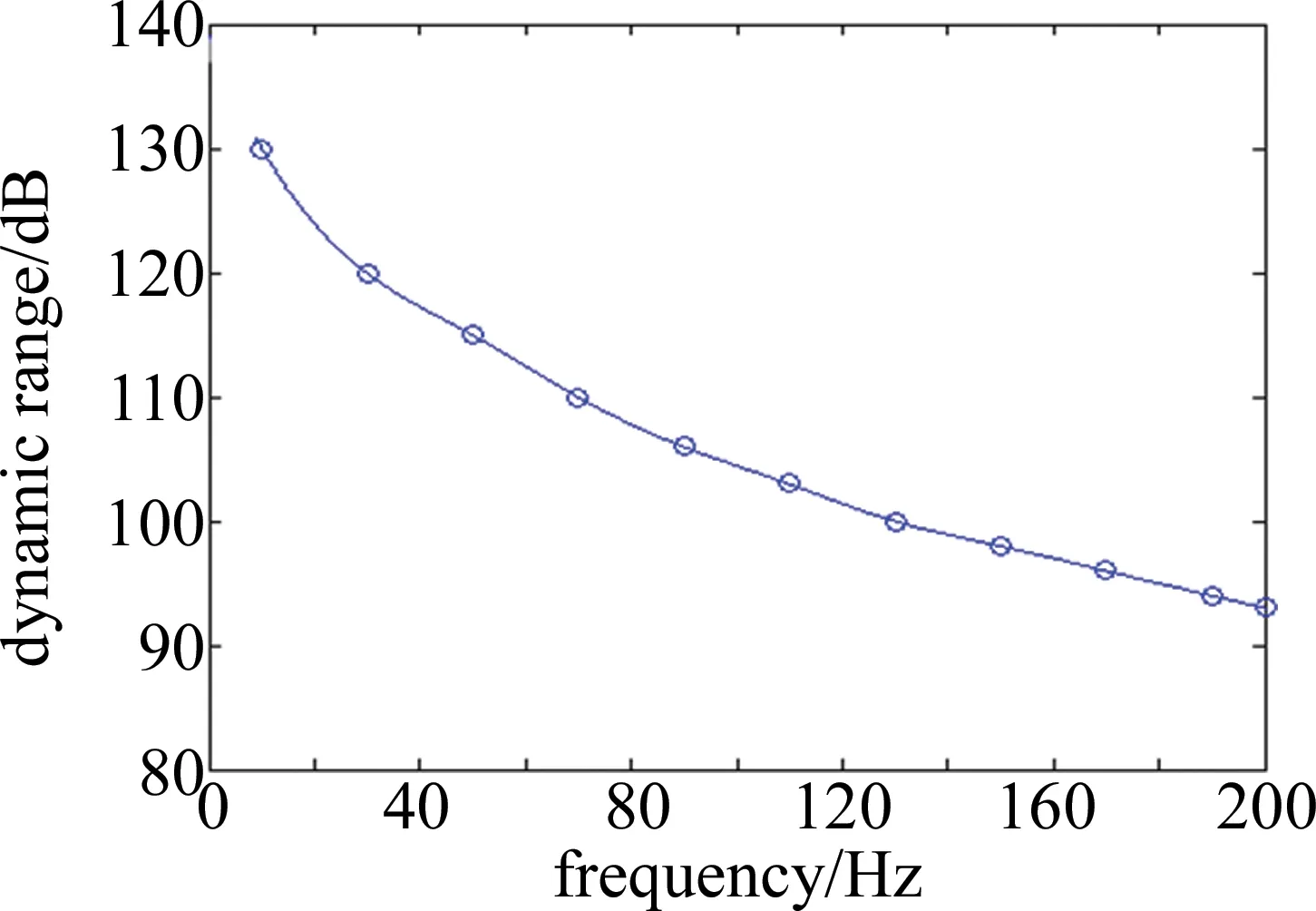
Fig.9 Dynamic range of PGC-improved demodulation algorithm

Fig.10 Linearity of PGC-improved demodulation algorithm

Table 1 Comparison of different algorithms

4 结 论

提出了一种基于反正切函数和微分自乘的改进型PGC解调算法。通过理论分析和相应仿真验证，研究了光强扰动和调制深度对解调性能的影响。改进后的PGC解调算法在低谐波失真和高稳定性方面都得到了验证。与传统的PGC-arctan算法和PGC-DCM算法相比，它具有更低的总谐波失真和更高的信纳比。对于从1.5rad～3.5rad宽范围的调制深度值，改进的PGC解调算法可以实现低于0.1%的低总谐波失真和30dB的高信纳比，线性度高达99.99%，比传统算法高出近10dB,比PGC-arccot-DSM高出5dB的信纳比，并且能够更好地抑制光强扰动，可以显著提高光纤传感器的性能。