高速铁路聚氨酯固化道床轨道不平顺数据分析

何庆 孙华坤 李晨钟 马玉松 王平 王凯

1.西南交通大学土木工程学院，成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；3.中国铁路济南局集团有限公司济南西工务段，济南 250021

轨道不平顺作为列车振动主要激扰源，直接影响列车运行过程中的平稳性和安全性。随着我国高速铁路的发展，对轨道平顺性的要求不断提升，为保证轨道在地质条件不利的特殊地段处仍能保持良好的平顺性，近年来发展出了一种新型聚氨酯固化道床技术。该技术在已达到稳定的新铺碎石道床空隙内灌注聚氨酯材料，使其沿碎石道床空隙渗入道床底部，在道床内经发泡、膨胀等过程，最终填满道砟间隙，形成弹性固结的整体道床结构。

聚氨酯固化道床本身累积变形较小，具有同混凝土整体道床相似的稳定性，通常短期内不需维护和修补，非常适合解决特殊路段平顺性表现差的问题［1］。然而由于施工过程控制不当，线下基础沉降，道床劣化等原因，线路高程随着时间的推移可能会发生较大变化，严重影响线路静、动态平顺性，需要定期开展检测并制定科学的养护维修计划［2］。

相关学者对聚氨酯道床的力学性能［3］、结构参数合理性设计［4］、整体道床的动力学指标［5］等开展了大量研究，但基于实测动检数据的轨道质量综合评价尚存在研究空白。文献［6］对国内某线路聚氨酯固化道床段实测不平顺进行分析，发现轨道质量指数（Track Quality Index，TQI）随时间推移受高低、水平、扭曲不平顺指标的影响变大，聚氨酯固化道床功率谱密度（Power Spectrum Density，PSD）特征波长小于无砟轨道。对固化道床整体区段TQI 的变动情况、状态发展趋势、指标超限程度、分波长超限分析、特征区段动力学指标分析等问题尚需要进一步研究。

基于此，本文从时域和频域的角度，借助峰值、TQI和PSD 对我国某条采用聚氨酯固化技术的高速铁路2019年间的18 次动检数据进行分析。在此基础上通过UM 建立车体轨道模型进行动力学仿真，分析平稳性与舒适性指标变化规律，为各铁路局养护维修工作提供技术支撑。

1 数据概况

受轮轨相对滑动、轮径尺寸误差、GPS局限性等因素的影响，轨检车系统最终得到的检测数据存在里程标识重复或者缺失等问题，造成里程误差累积，使轨道状态评价结果失真，不利于轨道预知性维护的发展。因此，采用汪鑫等［7］提出的多通道里程误差修正模型，结合曲线主点信息、超高值对原始数据进行里程修正。

所选线路设计速度350 km/h，在K203+950—K211+000区段对道床进行聚氨酯固化处理，且该区段整体处于反向曲线段，纵坡起伏最高达30‰。采用该线路2019年1月至11月轨道不平顺动检数据，检测速度平均290 km/h，采样间隔为0.25 m，包含左高低、右高低、左轨向、右轨向、水平、轨距、三角坑等多项轨道不平顺指标。在K120+000—K130+000选取一般道床区段，在K203+950—K211+000 选取固化道床正常区段和固化道床异常区段。对3种区段进行TQI、PSD和动力学指标计算分析。

2 评价方法与动力学模型

结合TQI 和PSD 两项指标，从时域和频域两个方面，对所选轨道区段的整体质量状态和不平顺波长信息、密度值等进行补充分析。采用核密度估计法定位识别最大异常里程位置，对其可能的劣化发展范围进行估计。同时，结合UM 动力学仿真，分析异常里程位置的动力学性能，从而全面比较固化道床与一般道床的轨道平顺性差异。

2.1 轨道质量指数与轨道不平顺功率谱

TQI 是7 项动态不平顺指标的统计结果，用来描述200 m 区段内轨道平顺性的离散程度，其值越大，离散程度越高，即平顺性越差。TQI值的计算式为

式中：i=1，2，…，7，分别代表左高低、右高低、左轨向、右轨向、轨距、水平、扭曲；σi为第i项轨道不平顺指标标准差。

σi的计算式为

式中：m为采样点的个数（200 m单元区段中m=800）；xik为200 m 区段内第i项轨道不平顺指标在第k个采样点处的幅值为第i项参数轨道不平顺指标均值。

轨道不平顺PSD 能够直观反映轨道不平顺的波长和幅值两方面信息，功率值的大小反映轨道质量状态，同一波长下功率值越小，轨道平顺性越好［8-9］。其计算式为

2.2 核密度估计法与预测带计算

作为非参数估计的一种，核密度估计法常被用于定位异常发生概率最大位置［10-11］。该方法会将每个样本点按核函数的分布进行估计，而后将多个出现在相近位置处的样本点的概率密度叠加，得到最大概率密度位置。概率密度函数的计算式为

确定核函数带宽h最优取值的计算式为

式中：M(h)为带宽的均方误差；f(x)为x位置处的密度函数。

预测带是以最佳拟合曲线为中心，在其上下等距离延伸得到的预测区间。95%预测带即为所期望包含95%未来数据点的区域。计算式为

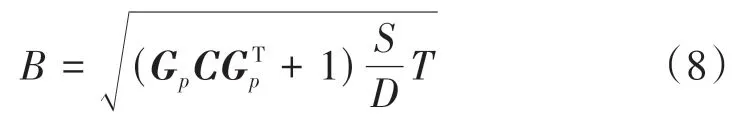
式中：B为预测带与拟合曲线的距离；Gp为特定p值下所有参数的梯度向量；C为协方差矩阵，每一项均是两项参数间协方差；S为拟合的平方和；D为自由度数值，数据点数减去参数个数；T为t 分布常数，置信度95%时取1.96。

Gp的计算式为

式中：Y为特定p值和所有最佳参数下拟合曲线中的Y值；P为梯度向量中包含的参数。

2.3 车辆-轨道耦合动力学模型

2.3.1 车辆与轨道模型

为获得轨道车辆在固化道床异常区段下的动力学性能，利用UM 软件进行建模。建模时对车辆构成、轨道线型、行驶阻力等参数进行设计［12］。车辆主要部件简化为刚体，包含车体、转向架和轮对等部件。在车体与转向架之间设置二系弹簧悬挂，转向架与轮对之间设置一系弹簧悬挂与阻尼。考虑轮对主要的运动形态为滚动，对车体转向架设置横移、侧滚、沉浮、点头和摇头5 个自由度，轮对不考虑点头运动，设置4个自由度。整车拓扑模型如图1所示。轨道模型采用连续弹性支撑的无质量轨道，将实测轨道不平顺数据与曲线数据等作为输入，设计轨道线型与行驶阻力。

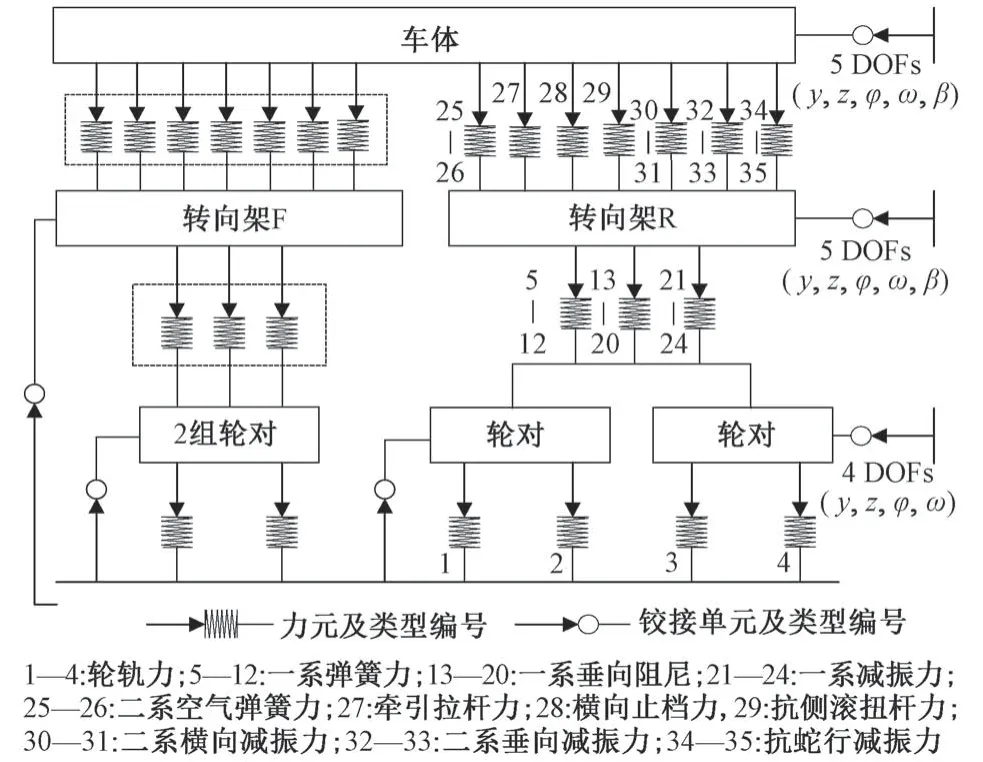
图1 车辆拓扑模型

2.3.2 轮轨接触模型

车辆模型与轨道模型间通过轮轨接触模型连接。该模型在UM 中采用Hertz 接触理论计算法向应力，采用FASTSIM 算法模拟单点接触，计算轮轨蠕滑力和蠕滑力矩，从而解决轮轨蠕滑非线性问题。

3 平顺性指标分析

采用上述评价方法对里程修正后数据进行计算，得到划分区段的TQI 和PSD 值。结合其他线路信息，以TQI时空分布矩阵、累计分布函数曲线、时间序列曲线、轨道谱拟合、功率分布统计等方式加以分析。

3.1 轨道质量指数

计算所取区段7 项不平顺指标的单项标准差和TQI 值。结合350 km/h 下既有线路TQI 及单项标准差管理标准，判断所选区段整体质量水平及其超限情况。为了更直观地比较各区段TQI 差异，将计算结果进行对数化处理。结合所取区段曲线超高和纵坡数据，最终建立了TQI时空分布矩阵，见图2、图3。

对比图2（a）、图3（a）可知：①空间维度上，一般道床段TQI 值随里程波动不明显，而固化道床段在里程K206+550—K209+750 处存在明显TQI 值激增和骤减（深红色部分），其值在2.5 ～4.5。固化道床段明显区分为两部分，即与一般道床段平顺性相近的固化道床正常部分和TQI值突变的固化道床异常部分。②时间维度上，二者TQI值差别较小，总体保持一致。

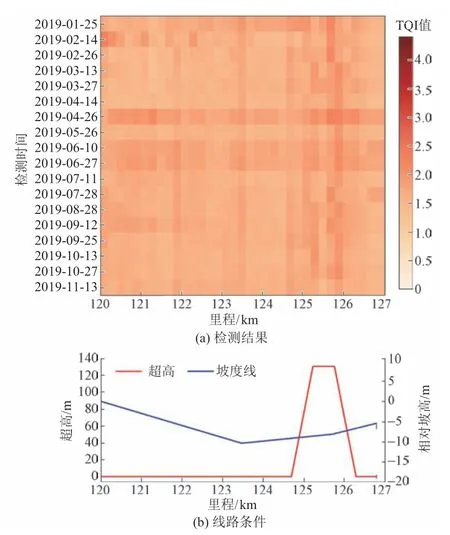
图2 一般道床TQI时空分布矩阵

图3 固化道床TQI时空分布矩阵

参照350 km/h 速度下的轨道质量指数管理标准（表1），对固化道床段的7项指标标准差进行计算。结果显示：垂向指标左高低、右高低和扭曲不平顺的标准差在部分异常位置存在部分时间下超限的状况，其他4项指标均属于正常水平。

表1 350 km/h下TQI限值管理标准 mm

对超限日期下的3项超限指标标准差进行累计分布计算，结果见表2。可以看出，左、右高低不平顺超限比例在5%以下，而扭曲不平顺超限比例最大已接近12%。当以75%管理值为限值时，左、右高低不平顺超限比例远小于扭曲不平顺，说明随时间推移，不平顺在垂向上会逐渐出现超限状况。其中，以扭曲不平顺受影响最大，超限速率最快，逼近限值数据最多。

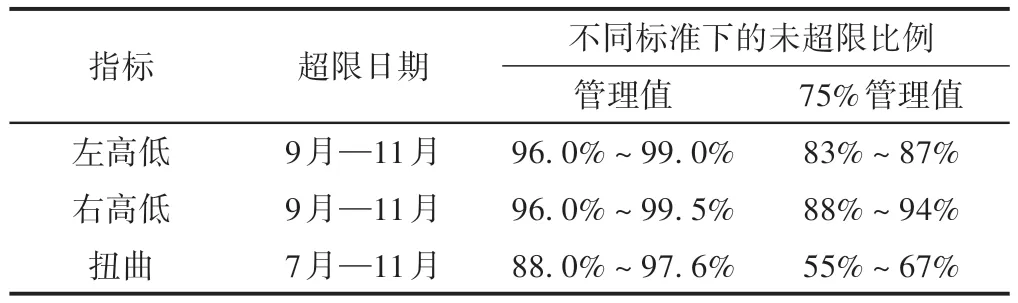
表2 垂向指标未超限比例

考虑3 项指标存在不同程度超限对固化段整体TQI 的影响，以所有检测时间下一般道床段TQI 均值加3 倍标准差作阈值，标定出固化道床区段内所有大于该阈值的疑似异常里程位置。对标定出的所有异常位置，采用核密度估计法进行统计分析，从而定位出异常峰值所在的里程位置。如图4（a）所示，概率密度曲线中具有两个明显峰值，提取这两个峰值对应里程下的时间序列数据。通过4 次多项式拟合的方法，得到拟合曲线并计算出对应的95%置信带和预测带，如图4（b）所示，进而对TQI发展趋势加以分析。

图4 TQI异常定位及趋势分析

由图4 可知，受3 项指标超限影响，异常峰值里程下TQI值在7月—11月呈上升趋势。依据95%预测带的计算结果，11月中后期在预测带的上限位置处，TQI可能会出现超限临界值。

3.2 功率谱密度分析

计算7项不平顺指标的PSD 及功率分布。以左高低不平顺的计算结果为例进行分析，截止波长取1 ～300 m。为了直观表示差异，将计算结果进行对数化处理。结果表明，同一区段内功率谱密度曲线重复性较好，波形相似。对所有检测时间下PSD 均值进行拟合，结果见图5。可知，5 m 以下的短波范围内，3 个区段PSD 差异较小；5 ～70 m 中长波范围内，固化道床异常段明显高于其他区段，3 个区段均在30 ～40 m 波长处达到峰值。

图5 轨道谱均值拟合结果

固化道床异常主要反映在5 ～70 m 中长波区域，可通过观察该范围内波长变化来判断道床是否存在不平顺异常变化。

对5 ～70 m 中长波段进行划分，计算各段功率值并进行统计分析，结果见表3。可知：固化道床异常段在各波段的功率分布范围、均值和标准差都要大于另两段；以偏度衡量，一般道床段的数据偏斜程度更大，选择略小于均值的值更能代表大多数数据分布情况；以峰度衡量，固化道床正常段和异常段的峰度较小，波峰更加平坦，选取均值作为功率代表值。

表3 各区段功率值统计指标

基于此，在各波段范围内，一般道床段取0.56、1.54、2.40、13.47 为各段功率代表值，固化道床正常段取 0.77、2.13、4.32、20.96，固化道床异常段取2.11、14.34、25.55、60.14 为各段功率代表值。计算结果显示，相比于一般道床段，固化道床正常段功率值增大约38% ～80%，固化道床异常段功率值增大约2.77 ～ 9.64倍。

4 UM动力学仿真分析

借助UM 动力学仿真软件，建立车体与多刚体无质量轨道耦合模型，分别控制实测不平顺、曲线信息等输入参数，分析不同道床区段动力学指标变化。仿真得到300 km 时速下稳定性指标轮重减载率和轮轴横向力，见图6。

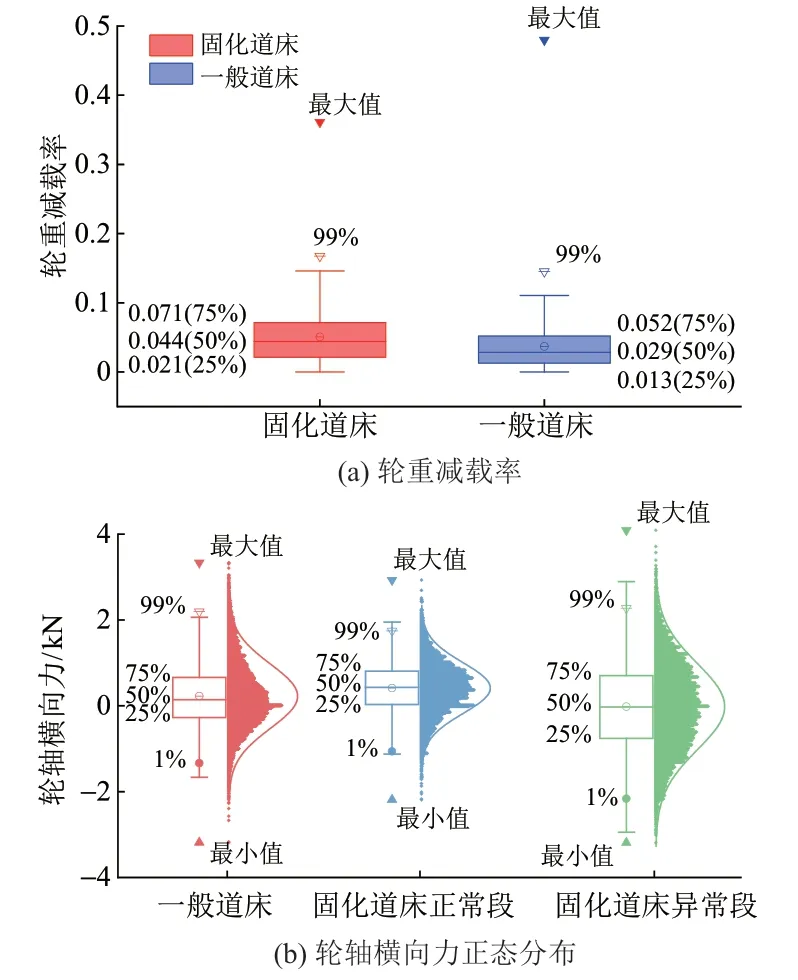
图6 安全性指标

由图6可知：排除异常值后，固化道床段轮重减载率比一般道床增大11% ～66%；车体进入固化道床异常段后，轮轴横向力波动性变强，轮轴横向力极差（最大值与最小值的差）分别为一般道床和正常区段的1.12、1.42 倍。去除个别异常值，以1%～99%的分位数计算时，异常段轮轴横向力极差分别增大42%和57%。

不同车速下，一般道床区段与固化道床异常段的横向、垂向Sperling指数见图7。

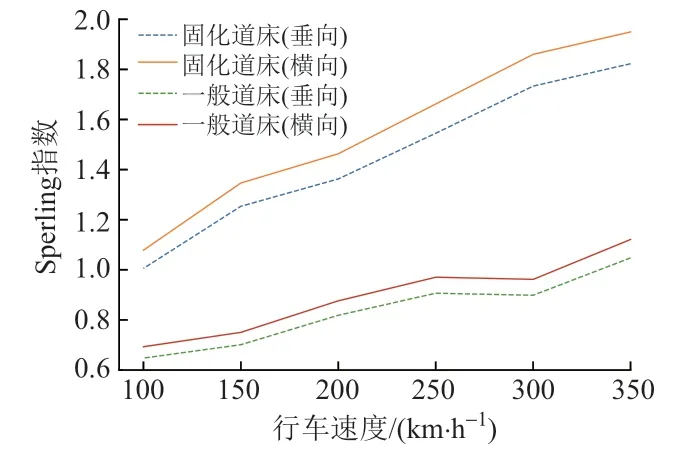
图7 不同行车速度下的Sperling指数

由图7 可知，随着速度提升，异常段Sperling 指数增速比一般道床段大1倍。参考整体线路设计时速为350 km，若继续劣化，未来此处极可能出现舒适性降级。

在建模过程中，对车体构成、轨道线型、行驶阻力等参数进行了设计，没有将轨道及下部结构考虑为柔性体，但是从车体动力学角度分析，该仿真过程足以满足工程需要。所得结论可以反映异常段线路在实际运行中可能出现的动力学问题，从而更全面指导养护维修工作。

5 结论

1）聚氨酯固化道床区段内TQI值存在突变。随时间推移，垂向指标标准差出现超限，其中高低不平顺最大超限比例约5%，扭曲不平顺最大超限比例约12%。当以75%管理值为限值时，扭曲不平顺超限速率及比例剧增，高低不平顺超限过程相对缓慢。

2）TQI异常峰值里程下，TQI值在7月—11月呈上升趋势；95%预测带的计算结果显示，11月中后期会在预测带上限处出现TQI临界值。

3）不同区段PSD 值在5 m 以下短波范围内差异较小；5 ～70 m 中长波内，固化道床异常段PSD 值大于其他区段。各区段PSD 值均在30 ～40 m 波长范围内达最大。

4）UM 仿真结果表明，车体进入固化道床区段后，去除异常值，安全性指标轮重减载率存在11% ～66%的增幅。固化道床异常段轮轴横向力相较于其他区段分别增大42%和57%；Sperling 指数的增速约增大1倍，继续发展未来极有可能出现舒适性降级。

铁路工作人员对该聚氨酯固化道床线路的养护维修可结合动力学分析结论，着重针对垂向指标进行。道床采用的聚氨酯材料老化后如何维护处理，何种因素会导致聚氨酯材料劣化进而影响轨道平顺性，以及对轨道结构的仿真建模，需开展进一步研究加以完善。