固体力学的发展及其在航空航天工程中的应用研究

杨泽天

（重庆大学，重庆 400044）

1 固体力学及其发展趋势

固体力学是以牛顿力学为基础的一门学科。它主要研究固体介质在外界因素作用下的应力、应变以及破坏等的规律。固体力学广泛应用于工程领域。不仅是机械和土木工程系统的基础，同时，它是生物医学、石油、电力、航空航天、制造业和核技术、化学以及材料科学、地球物理学和固体物理学等许多工学学科研究中有用的工具。固体力学同时具有基础科学和技术科学的性质，一方面，作为技术科学对于生产生活做出贡献；另一方面，作为基础科学与其他学科交叉融合发展，不断创造出新的分支学科。

固体力学理论的发展经历了四个阶段：基本概念的形成阶段；具体问题的解决阶段；一般理论、原理、方法和数学方程的发展阶段；探索复杂问题的阶段。在飞机、船舶、核反应堆和大型建筑的高精度要求下，许多科学家参与了机械研究并解决了各种复杂力学问题。随着科学技术的发展，新的科学技术领域与传统的力学研究问题有很大的不同。其中之一是研究对象的大小不同。纳米技术和生命科学等许多学科都参与了纳米和微器件的设计和制备。其次，物体的变形和运动不仅是由于力场的影响，而且往往是由于多个力场的耦合。最后，物质往往具有很强的相各向同性和非均匀性。因此，能否将固体力学应用到不断发展的科学技术领域，是固体力学面临的挑战之一。到如今21世纪固体力学的研究对象不再是单一的简单的，而是跨尺度的和复杂的；研究手段必须克服传统思维的局限性，具有跨学科、跨学科、系统思维的特点；研究成果将在人类科技进步和社会发展中发挥不可预测的作用。

2 固体力学发展现存问题

2.1 重基础轻研究，重理论轻实验

固体力学的边界原理相互交叉，新学科的生长点十分突出。然而，我们需要把重点放在迫切需要突破的关键问题上，例如，航空航天材料和结构的主要力学问题的研究。虽然国家给予资金优先，但与理论计算相比，实验研究项目申请资金的比例仍然很小。

2.2 没有解决固体强度问题

虽然固体力学能够科学、完整地描述材料的理论强度和回弹，但材料的实际强度往往和理论强度有较大出入，最终使得在工程应用中用较大的安全系数来确保安全。特别是在航天领域，火箭的各种部件普遍使用较大安全系数，增加了大量起飞重量和发射成本，降低了载荷投放能力。但目前对这一问题的重视还不够，导致疲劳和断裂力学的应用项目占比较低。

3 固体力学在航空航天工程中的应用

理论来自实践，包括固体力学。固体力学的发展同时也给解决航空航天技术领域的一些重要问题带来了一些新思路，为了这证明这种思路的有效性，本文探讨了计算固体力学在航空航天技术中的应用。

3.1 航空航天工程中的应用

（1）广布疲劳损伤蔓延的断裂力学计算。飞机构件的耐久性不但取决于构件内部应力大小,还取决于构件细节的抗疲劳特性。构件耐久性则是指飞机构件经受断裂、侵蚀、热分解、剥落以及异物破坏的能力。断裂疲劳是影响飞机构件在正常工作环境下使用寿命的最主要原因之一。其评价方式为疲劳分析方法和断裂力学分析。疲劳分析方法的主要目的在于实现结构的长寿命设计。它还能够确保某些无法满足损伤容限条件的不可测量构件的安全。损伤容限允许结构中存在一些初始裂纹，在正常使用的重复载荷作用后，裂纹的增长应在一定的限度内，满足剩余强度要求。

机身和机翼的设计制造中有许多如舱门和舷窗的开孔件，这些开孔件类似机身的各个连接处一样容易引起局部的应力集中。在零件的生产加工过程亦或是飞机的日常使用过程中，在这些部位会产生很多细小的裂纹，在重复加载的过程中，这些裂纹会逐步拓展。这种因同时存在的大量裂纹导致材料不满足剩余强度要求的问题称作广布疲劳损伤。分析广布疲劳损伤的问题，有助于确保飞机构件的强度和安全。广布疲劳损伤的分析分为两部分：关键结构部件的有限元数值分析和实验验证。以机翼蒙皮连接处有限元计算为例，如图1所示。

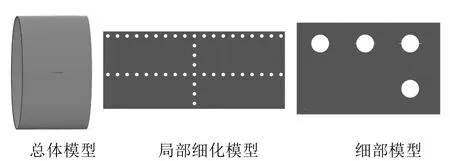
图1 机翼蒙皮疲劳损伤蔓延分析

首先,建立总体模型,接着建立局部细化模型,最后再建立细节更充分的细化模型。在整个计算流程中,先用有限元法分析总体模型以及局部细化模型，然后，将分析的应力应变结果输入细化模型中进行断裂力学分析,评判裂缝是否会扩展。图2显示了局部细化模型的应力和变形分析结果。

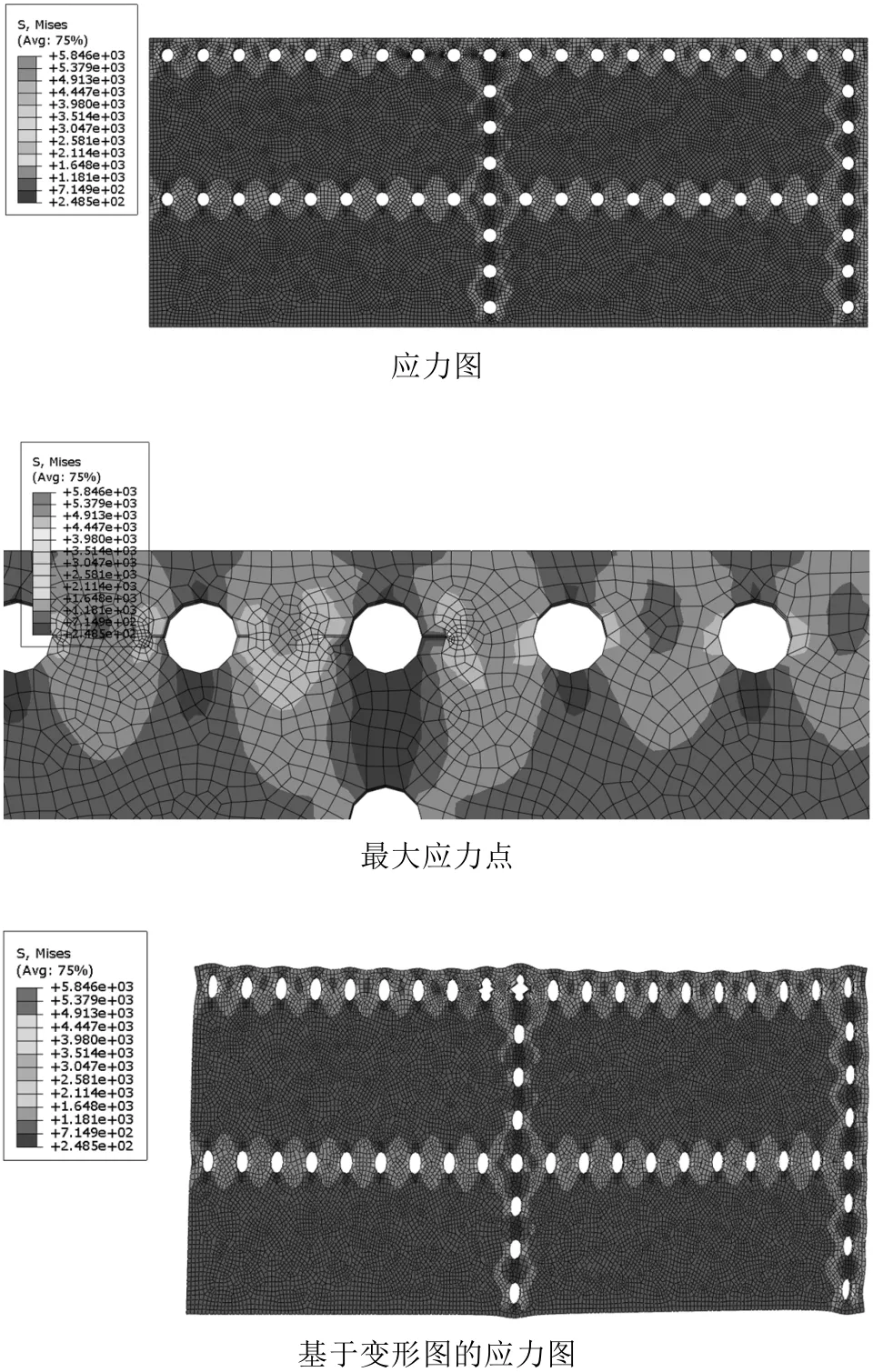
图2 局部细化模型的应力和变形分析结果

将计算分析结果与部分试件的实验数据进行比较，评估飞机结构疲劳损伤扩展的风险，最后提交分析报告和试验结果，由此判断飞机结构是否满足适航要求。

有限元计算是计算固体力学的核心课题。过去的几十年里，许多商业有限元软件已经被开发用于此类计算和分析，如ABAQUS、ADINA和ANSYS等。

（2）应用于反问题。力学系统是反问题的主要应用领域。众所周知，在力学系统中，对正问题的研究无论是在理论还是在算法上都达到了较完善的水平，而这正是提出反问题的基础。另一方面，反问题也是力学研究的热点话题。“因为在工程实践中，人们真正感兴趣的不是正问题，而是反问题”。

计算力学随着现代计算机性能的提升以及普及的过程中逐渐发展并完善。它与反问题的发展背景较为类似。这些是计算机技术迅速发展后产生的新学科，它们是在经典数学方法难以处理实践中提出的大量问题时发展起来的。计算固体力学的发展大大拓宽了数学模型在力学系统中的应用范围。

非线性模型的数值解以及各种成像和仿真技术可用于探索许多复杂力学系统的内部机理。在此基础上，如果我们在实践中进一步深入，将会出现许多反问题。这是因为许多可以在理论上或实验室中给出的条件在实践中往往难以给出。不研究它们会妨碍理论的应用。可以说，反问题的求解是从理论模型过渡到实际应用的一个不可或缺的环节。目前，即使是典型的偏线性微分方程的反问题也没有得到系统的解决，这引起了计算力学专家的关注。

让我们举个例子来说明这一点。龚尧南教授在他的报告中提到了重返大气层的路线规划。路线必须确保受力结构的瞬时温度不超过规定值。我们如何确定结构的瞬时温度？必须已知飞机返回大气时摩擦热产生的边界瞬时温度（第一类边界条件）或瞬时热流（第二类边界条件），然后，通过热传导方程的解进行计算。然而，由于技术原因，很难使用传感器实时测量边界上的这些温度值。但是，可以在结构的某些点测量瞬时温度。

如何根据这些条件计算边界热流或瞬时温度是一个典型的反问题。即使它是线性的，也不容易求解。James V.Bcck教授研究这一主题已有20多年，并就此主题撰写了一本专著。这个例子表明，为了解决极其复杂的实际工程问题，不可避免地会遇到反问题。因此，研究反问题的理论和解法将促进计算力学的应用和发展；相反,由于反问题的解决是建立在正问题成熟的基础上，而计算力学是解决正问题的有力工具,因此,计算力学理论和方法的创新,特别是新软件的开发，提供先进的计算工具来解决反问题。因此，反问题与计算力学相辅相成、相互促进。

3.2 应用案例——以主控制技术为例

主动控制技术有着广泛的应用，如自动控制理论、随动系统设计等。在当今的航空航天技术中，主动控制技术可以起到地形监测和提高飞行稳定性的作用。当计算固体力学应用于它时，应考虑到流体-固体的耦合问题，模型的选择以及算法的优化等方面。

同时，因控制系统对飞行器整体结构稳定性有一定的影响，应进行整体和局部的结构力学分析。对于主控制技术而言，理论分析的准确性以及分析速度都具有重要意义。

4 结语

综上所述，在国民经济和社会发展的影响下，航空航天产业具有巨大的发展潜力。计算固体力学作为计算力学和固体力学的交叉学科在工程领域有着非常频繁的应用，特别是在航空航天工程中。本文首先分析了固体力学的理论发展，然后，从存在的不足、与航空技术有关的应用、反问题和主控制技术四个方面介绍了计算固体力学在航空技术中的实际应用。