微电机永磁转子转动惯量测试研究
袁永杰,郑文鹏,李立娜,蒋梅平
(中国电子科技集团公司第二十一研究所,上海 200233)
0 引 言
电机转动惯量是表征电机工作特性的一项重要参数,与电机的起动过程、机电时间常数都有密切关系。电机转子由多种材料构成,且形状存在不规则性,因此需要在设计完成后测试转子的转动惯量,以便更为准确地计算电机其他相关参数。
测试转动惯量可分为在线测量和离线测量两类。常用的在线测量方法包括瞬时转速法、附加质量法、功率法等,对于电机而言,永磁转子部件装入电机后会存在齿槽转矩、摩擦转矩等因素,因此在线测量法一般不适用于带磁电机转子的转动惯量测试。而离线测量方法包括单线扭摆法、三线悬吊法、落体法等[1],按照GJB 361B—2015《控制电机通用规范》中的要求,控制用微电机转动惯量测试方法选取了较为简单方便的单线扭摆法(扭转振荡法)和三线悬吊法。但对于带磁转子而言,无论哪种转动惯量离线测量方法,都无法消除地磁场对磁性转子的影响,测试结果会出现一定偏差,且转子自身惯量越小,磁钢磁性越强,偏差越大。
为消除地磁场的影响,通过多种方法的尝试,最终确认通过高温去磁后的转子,使用单线悬吊法测试其转动惯量的测试结果与理论计算值相符合。另外通过分析可知,屏蔽大地磁场也可以实现带磁转子的无损测试。
1 无磁转子部件单线悬吊法测试惯量原理
对于微型电机,转子绕轴心对称且转子无磁性的情况下,一般采用单线扭摆法测试转子转动惯量。该方法相对其他转动惯量测试方法而言,测试过程操作简单,且成本较低,经济实惠。单线扭摆法的测试原理如图1所示,选用伸展性小、弹性好的钢丝作为悬吊线,一端固定,另一端与连接件相连接,连接件再与被测转子部件相连接,连接后保证连接件和电机转子与悬吊线同轴旋转。

图1 单线扭摆法测试转动惯量示意图
此时,对被测转子部件施加水平力偶矩,则连接件和电机转子将绕轴线往复摆动,其运动微分方程[2]:
M=Jβ=-Kθ
(1)
式中:M为连接件和被测电机转子的转矩;J为连接件和被测电机转子的转动惯量;β为连接件和被测电机转子的角加速度;θ为连接件和被测电机转子的角位移;K为系统扭转模量,K=Gπd4/(32L),G为切变模量,d为悬吊线直径,L为悬吊线长度。
由于系统阻尼较小,在可以忽略且无其他外力的情况下,根据简谐振动的动力学特性,即β+ω2θ=0,可知被测转子部件和连接件的摆动角速度ω和摆动周期T如下:
由此可知,被测电机转子和连接件的转动惯量:
(2)
由式(2)可知,在悬吊系统确定的情况下,转动惯量仅与摆动周期的平方成正比。因此在已知悬吊线扭转模量的情况下,可以通过测试被测件的摆动周期计算出被测物体的转动惯量。若不知悬吊线的扭转模量,则可以测试已知惯量的摆动周期和被测惯量的摆动周期,通过对比法计算出被测物体的转动惯量:
(3)
式中:J被测转子为被测转子的转动惯量;J已知惯量为已知对比物体的转动惯量;J连接件为连接件的转动惯量;T1为被测转子和连接件的摆动周期;T2为已知对比物体和连接件的摆动周期。
由式(3)也可以看出,若使用对比法测试转动惯量,已知物体的惯量应接近被测物体,且二者应有近似的长径比,使得系统阻尼差异更小。在忽略系统阻尼的条件下,单线扭摆法测试转动惯量的误差主要受到摆动周期、悬吊线的直径和长度的影响。因此悬吊线应尽量选用长而细、弹性好、内阻尼小的弹簧钢丝,并采用尽可能精确的周期测试方法。
2 带磁转子部件对测试结果的影响分析
若转子部件包含永磁体,则永磁体和大地磁场的相互作用,破坏了单线扭摆形成的简谐振动,转子最终的摆动周期的平方不能与转动惯量成正比。
假设磁性转子对外呈现出一对极,磁感应强度为B2,大地磁场为均匀磁场,磁感应强度为B1,它们之间的夹角为θ,如图2所示。
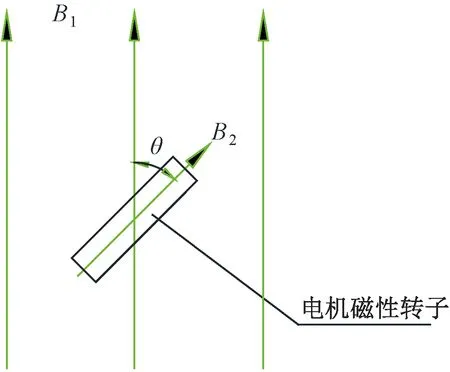
图2 磁性转子在大地磁场中的受力分析
其合成磁场的磁感应强度:
对应的磁场能量密度:
根据虚功原理,磁钢受到的转矩:
(4)
大地磁场在磁性转子上施加了转矩M′,该转矩的大小与地磁场的磁感应强度B1、转子永磁体的磁感应强度B2成正比,且该转矩始终指向大地磁场,在转子磁场偏离大地磁场时,转矩增大。此时简谐振动的动力学特性不复存在,即β+ω2θ0。
电磁转矩M′使得式(1)变化为式(5):
M+M′=Jβ=B1B2/(μ0sinθ)-Kθ
(5)
且由于电磁力总是指向地磁场,简谐振动回复力叠加电磁力,该电磁力作为阻尼力,会破坏谐振,谐振周期缩短并迅速停止,因此对带磁转子部件的转动惯量测试会出现比实际值偏小的情况,偏小多少需要看电磁转矩M′与简谐振动往复转矩M的相对大小。当被测物体的转动惯量较大时,其往复转矩M较大,电磁转矩M′占比不大的情况下,其测试出的转动惯量值差异不大。当被测物体的转动惯量较小时,其往复转矩M较小,电磁转矩M′占比较大的情况下,其测试出的转动惯量值差异较大。
3 实验验证
选取三个不同转动惯量的带磁转子进行对比测试,实物图如图3所示。转子参数如表1所示。

图3 三个不同转动惯量的带磁转子

表1 带磁转子参数
按照单线扭摆法测试转子的摆动周期,并与标准惯量摆动周期进行了对比测试,标准转动惯量、连接器转动惯量及测试周期如表2所示。

表2 带磁转子和标准转动惯量的单线扭摆法测试参数
从表2可以看出,带磁转子由于与自身磁场与地磁场的相互作用,其电磁力对简谐振动产生阻尼,使得简谐振动周期加快,所测振荡周期与标准转动惯量相去甚远,以至于转子A和连接器的测试转动惯量小于连接器自身的转动惯量,带磁转子的转动惯量出现了负值。而当被测件的转动惯量逐渐增大时,地磁场的影响会逐渐减小。因此带磁转子、特别是小惯量的带磁转子,其转动惯量使用单线悬吊法不能准确测出。
4 其他离线测试方法对带磁转子转动惯量测试的影响分析
4.1 三线悬吊法
三线悬吊法是将转子置于一个圆的或等边三角形的平板上,使转子轴线与平板垂直并处于平板中心,平板质量约等于转子质量,平板与水平悬挂面用三根等长且相互平行的线相连接,如图4所示。然后将平板扭转一个小的角度,使其绕轴线扭动,测定其振荡周期T,用同样的方法测定不带转子时平板的振荡周期Tb,转子的转动惯量如式(6)所示[3]:
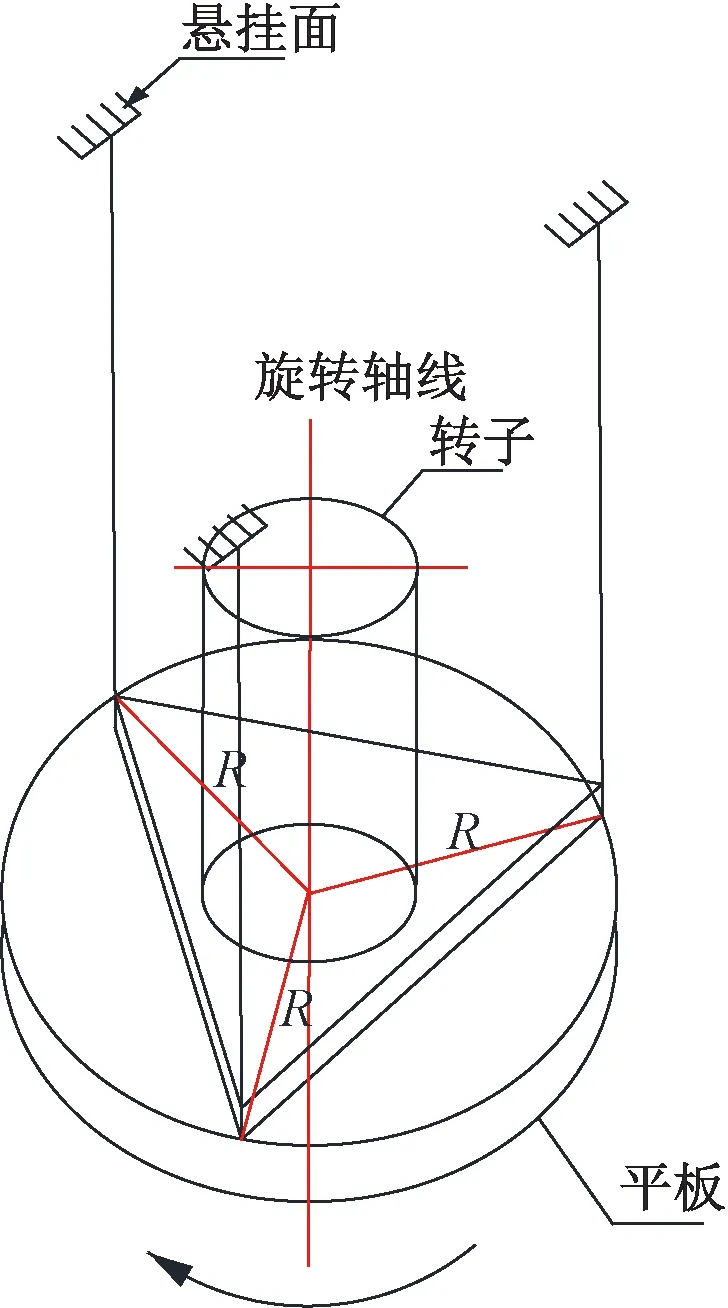
图4 三线悬吊法测试示意图

(6)
通过以上可知,三线悬吊法的测试原理仍然为利用不同物体惯量与其简谐摆动周期平方成正比的特性,通过已知惯量物体,分别测试出被测物和已知惯量的振荡周期来计算被测物体的转动惯量。而带磁转子和地磁场的相互作用,使得简谐振荡动力学特性不复存在,也不能有效测试出带磁转子的转动惯量。
4.2 落体法
落体法是将质量为m、半径为R的被测物体转轴两端自由支撑起来,在被测物体外圆上绕一条柔软而不易伸展的细绳,细绳的一端固定在被测物体的外沿上,另一端固定在质量为m1的重物上,如图5所示。

图5 落体法测试示意图
构件受落体重力的作用,作匀角加速度运动,根据牛顿运动定律,细绳上有如下平衡关系[4,5]:
FR=Jβ+M0
式中:F为细绳上的拉力;R为绕线半径;J为被测物体转动惯量与系统转动惯量之和;β为回转体的角加速度;M0摩擦转矩和空气阻转矩。
被测物体的转动惯量可表示:
J=(mgR-mβR2-M0)/β
落体法的缺点在于误差较大,主要误差在于被测物体转动和滑轮转动使用的轴承的阻力以及线轮和细绳之间的摩擦阻力[1]。对于转动惯量较大的被测物体,阻力转矩M0可以被忽略,测量准确度较高,对于小惯量的被测物体,测量误差较大。
对于微电机转子等小惯量的被测物体,并不适合使用落体法进行测试,且微电机的带磁转子在转动过程中同样会受到地磁场的影响。
为去除地磁场的影响,既可以通过去除转子本身永磁体的磁性,也可以通过屏蔽大地磁场两种方法来实现,下面逐一进行分析。
5 转子永磁体去磁
为去除地磁场对带磁转子的影响,采用高温去磁法去除了转子A、B、C的永磁体磁性。然后重新使用单线悬吊法测试三个转子的转动惯量,结果如表3所示。
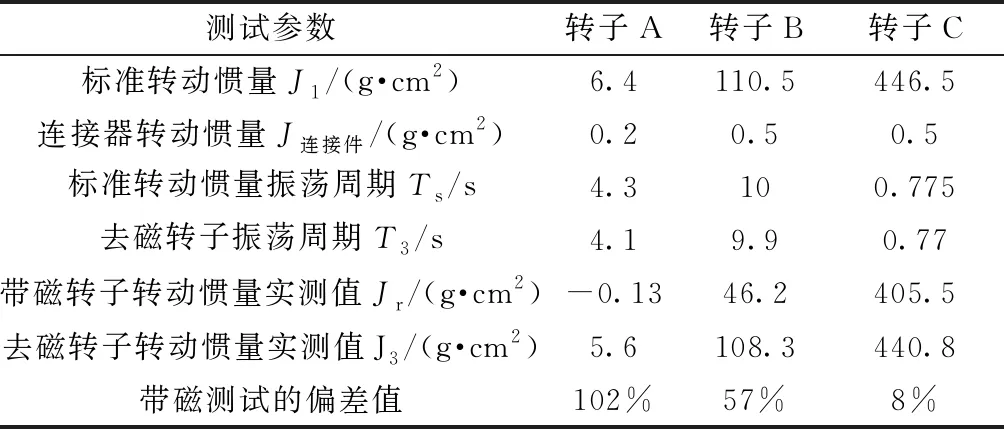
表3 带磁转子、去磁转子和标准转动惯量的单线扭摆法测试结果
从表3可以看出,去磁前后三个转子的转动惯量测试值存在一定的差异,去磁后三个转子的转动惯量与标准惯量基本相当,说明了去磁后的测试结果的准确性。而带磁情况下,当被测件的转动惯量逐渐增大时,地磁场的影响会逐渐减小,如转子C,去磁前后转动惯量差异仅为8%。因此通过高温等去磁手段将转子永磁体去磁后,使用单线悬吊法可以较为准确地测试出转动惯量。
6 屏蔽大地磁场
高温去除永磁转子的磁性后可以准确地测试出转子的转动惯量,但高温去磁后的转子基本无法再使用。而通过屏蔽大地磁场,亦可以较为方便准确地测试出带磁转子的转动惯量,且对转子没有损伤。
通过屏蔽无法完全去除地磁场(约0.05~0.06 mT),达到所谓的零磁环境(磁场为绝对零值的环境),但对于工程计算和测量来说,屏蔽掉90%以上地磁场的弱磁环境亦可以满足计算精度。国际上已经能够仅用2层或3层高导磁和高导电材料屏蔽99.99%以上的地磁场,即在房屋尺寸的空间中实现nT量级剩余磁场和fT 量级磁场噪声[6]。然而,该量级的近零磁环境建设或使用费用极高,不适合工程化的需求。
通过亥姆霍兹线圈可以实现特定区域内的均匀磁场,若该磁场与地磁场大小相等,方向相反,即可以实现对地磁场的屏蔽。一维亥姆霍兹线圈是由一对半径R、匝数N均相同的线圈组成,两线圈彼此平行且共轴,线圈间距离正好等于圆形线圈的半径R,根据毕奥-萨伐尔定律,亥姆霍兹中轴线上距离中心点为z位置的磁感应强度[7]:

式中:μ0为真空磁导率;N为线圈匝数;I为通过线圈的电流。两个线圈产生的磁场叠加后,会在轴线上以中点为中心有一定的距离磁场强度不变,即形成了一个区域的恒定磁场,其值为B0。
通过调节N和I,可以实现B0与地磁场在该方向的分量大小相等,方向相反。因此,使用三维亥姆霍兹线圈可以抵消大部分地磁场,即去除98%以上的地磁场,在线圈内部建立一个弱磁区域,其剩余磁场可以达到10-6T甚至更低,完全可以用于带磁转子的转动惯量测试。
7 结 语
使用单线扭摆法测试微电机带磁转子的转动惯量时,由于地磁场的影响,振荡形成的简谐振动发生了改变,振动周期缩短,因此转动惯量实测值较实际值偏小。
偏差的大小和电磁力与简谐摆动力的比例相关。在电磁力远小于简谐摆动力的情况下,摆动周期和转动惯量与实际值相比变化不大;而在电磁力接近甚至大于简谐摆动力的情况下,摆动周期和转动惯量与实际值差异较大。换句话说,当转子转动惯量越大,其地磁场的影响越小,当转动惯量超过440.8 g·cm2时,其带磁转子实测转动惯量与无磁情况下仅差8%。
三线悬吊法同样不适合于带磁转子的测试,而落体法在测试惯量较小的物体时误差较大,也不适合于较小转动惯量的测试。
通过高温去磁使得转子上的永磁体退磁,然后进行转动惯量的测试,单线悬吊法是可以较准确地测试出转子转动惯量。
在不破坏转子的情况下,通过使用三维亥姆霍兹线圈屏蔽地磁场,理论上也可以消除地磁场的影响,得到较为准确的结果。

