软岩浅埋隧道锚开挖方案比选研究
李耘宇 申裕峰 李之达 王广群 彭浩雄 梁 倩
(武汉理工大学交通与物流工程学院1) 武汉 430063) (武汉市水务建设工程有限公司2) 武汉 430021)
(武汉电力职业技术学院3) 武汉 430070)
0 引 言
隧道锚作为悬索桥主要承载构件,在主缆巨大拉拔荷载作用下锚塞体与围岩共同受力,形成一个有机的受力系统[1].与常规隧道不同,隧道锚通常与水平面有较大倾角,形状为楔形属于变截面且越往隧道深处断面越大.上述特点导致隧道锚的施工工法选择,相比于常规隧道需要更具准确性、合理性.
目前,针对不同形式隧道的开挖方案选择研究,学者们已经取得了一定的成就.李俊达等[2]使用案例推理技术,建立了铁路隧道开挖方法的辅助决策模型.黄维新等[3]通过分析比较了不同开挖顺序,对软岩隧道各阶段施工过程中围岩变形量的影响.李昀等[4]借助反演分析方法得到数值模型参数,对台阶法开挖和全断面开挖进行了方案比选分析.孟哲玮等[5]采用荷载-结构法的二维有限模型,比较分析了溶岩大断面隧道的不同开挖支护方案.申灵君[6]以湘桂铁路扩改工程大坪隧道为工程背景,对软弱地层大断面隧道的交叉中隔壁(CRD)法和三台阶法两种施工开挖方案,进行多维度的比较分析,论证了在软弱地层大断面隧道施工中运用三台阶七步法的可行性.
但是,对于具有大倾角、软弱岩层且埋深较浅的复杂地层隧道式锚碇的开挖方案研究较少.文中以伍家岗长江大桥北岸隧道锚为研究对象,采用层次权重决策分析法,对隧道开挖施工过程中的围岩变形沉降、施工难度、施工速度、工程造价进行比较分析,并结合数值分析软件FLAC3D对三台阶法、三台阶临时仰拱法、正台阶环形开挖法和CRD法进行数值模拟,得到四种开挖方案下的围岩变形、应力和塑性区大小.通过对比层次权重决策分析法的分析结论和数值模拟的计算结果,为软岩浅埋隧道锚开挖工法选择提供科学指导.
1 工程概况
伍家岗长江大桥为跨度1 160 m的钢箱梁悬索桥,北岸采用隧道式锚碇,南岸采用重力式锚碇结构.隧道锚由洞口、前锚室、锚塞体和后锚室组成,整体呈前小后大的楔形状.隧道锚结构图见图1,其轴线长度90 m,轴线与水平面倾角为40°,后锚室距设计路面最大埋深为80 m,前锚面尺寸为9.04 m×11.44 m,后锚面尺寸则为16 m×20 m.
隧道锚场地区基岩裸露,主要为罗镜滩组杂色中厚至巨厚层状砾岩夹砂砾岩或含砾砂岩及砂岩,锚塞体整体位于微风化岩层,岩体的饱和抗压强度为15 MPa,抗剪强度0.7 MPa,属较软岩-软岩.地层总体近水平,产状倾向SE125°~143°、倾角4°~7°,岩体内构造不发育,未见断层和裂隙,隧道锚所处山体整体稳定性较好.
2 层次权重决策分析方法下开挖方案选择
2.1 结构开挖方案初选
伍家岗长江大桥北岸隧道锚,大倾角、变截面的结构特点给隧道施工带来较大困难,因此就施工机械的操作性和出渣的便利性而言,台阶法较为合适.同时考虑到洞口段的围岩情况,和锚塞体段大断面的特点,CRD法较为合适.由于前锚室段的截面尺寸较小,适合于简单台阶法开挖.综合考虑以上方法特点,再结合锚塞体对围岩整体性较高的要求下,初步确定三台阶法、三台阶临时仰拱法、正台阶环形开挖法和CRD法,作为隧道锚的开挖方案进行比较选择,四种开挖方法下的开挖断面图见图2.

图2 不同开挖方法下的开挖断面图
2.2 基于层次权重决策分析方法的开挖方案量化分析
层次权重决策分析方法能将一个多目标决策问题分解为多个目标,进而分解为多向指标的若干层次,通过定性指标算出层次单排序和总排序,以优化多方案决策问题[7].
具体比选步骤为:
步骤1建立目标分层结构,即相应的比选方案和评价指标,目标分层结构图见图3.

图3 层次权重决策分析法目标分层结构图
步骤2建立两两比较的判别矩阵 在统一评价指标下各施工方法之间的难度对比见表1.

表1 开挖方法对比表
根据评价指标将开挖方案两两比较,给出比分值然后确定判断矩阵B如下.
(1)
元素bij的确定方法:若开挖方法Pi与Pj优劣相当,则bij=1;若开挖方法Pi略优于Pj,则bij=3;若开挖方法Pi优于Pj,则bij=5;若开挖方法Pi甚优于Pj,则bij=7.同理,若开挖方法Pi稍劣于Pj,则bij=1/3;若开挖方法Pi劣于Pj,则bij=1/5;若开挖方法Pi甚劣于Pj,则bij=1/7,重要程度介于中间时可取中间值.
对于不同的评价指标,各开挖方案的排序有所不同,具体就施工难度C1而言P1>P3>P2>P4,根据沉降变形C2则是P4>P2>P3>P1,同样对于C3施工速度为P1>P2>P3>P4,工程造价C4所对应的方案排序为P1>P3>P2>P4.根据以上原则和排序构建各评价指标的判别矩阵见表2.

表2 各评价指标下判断矩阵
步骤3一致性检验 为尽量降低判别矩阵中元素取值的人为性影响,需要利用特征值检验判别矩阵一致性差异是否满足要求,即首先计算判别矩阵最大特征值λmax,再利用式(2),计算检验数CI,若CI<0.1,则认为所列判别矩阵是满足要求的.
(2)
通过计算得到各判别矩阵最大特征值λmax,和检验数CI见表3.

表3 一致性检验结果
步骤4确定开挖方案总排序 确定开挖方案总排序时,以变形沉降量大小和工程造价为主要考虑方面,且处于安全性考虑,控制变形沉降量权重将大于工程造价权重,根据相对权重计算公式求出层次单排序和总排序的结果,排序见表4.

表4 层次权重决策分析法下开挖方案总体排序
由表4 可知:当目标指标着重于变形沉降C1和工程造价C4时,开挖方案中体排序结果为三台阶临时仰拱法P2最优,CRD法次之;就着眼于控制变形沉降量而言CRD法效果最好,这也符合工程实际逻辑.因此层次权重决策分析法下伍家岗长江大桥北岸隧道锚开挖最优方案为三台阶临时仰拱法.
3 数值计算模型
3.1 计算模型及参数
使用计算软件FLAC3D,结合工程地质资料建立数值分析模型,模型以桥梁中心线为X轴,根据圣维南原理岩体开挖后的应力-应变只对3~5倍开挖断面边长的范围内的岩体有影响[8],在该范围之外可近似认为岩体所受应变为零.故取计算模型的范围为240 m×150 m×150 m,X轴取前锚室前端中心点正方向135 m,负方向105 m,Y轴取垂直桥梁中心线左右两边各75 m,Z轴从高程-60 m至地表.
岩体采用Mohr-Coulomb本构模型,用实体单元模拟,通过六面体为主的单元进行网格划分;衬砌采用线弹性本构模型,用shell单元模拟;锚杆采用线弹性本构模型,用cable单元模拟.由于隧道锚属于浅埋型隧道,其构造应力场很小几乎可以忽略,所以在模拟分析时仅考虑自重应力场的作用.
模型中围岩力学参数的设定,将会直接影响到隧洞的拱顶沉降大小和洞周围岩的收敛情况[9],而隧道锚初期支护采用锚杆+钢拱架+钢筋网+喷射混凝土的支护方式,因此需要将钢拱架的支护作用根据等效原则增加到喷射混凝土的力学参数中,其等效方法按照式(3)计算,得到模型材料计算参数表,见表5.

表5 数值模型材料计算参数表
(3)
式中:E为折算后结构弹性模量;E0为喷射混凝土弹性模量;Eg为钢拱架弹性模量;Sg为钢拱架横截面积;Sc为喷射混凝土横截面积.
根据以上材料参数建立四种开挖方案下的数值模型,其不同的开挖支护模拟图见图4.模拟开挖时开挖时严格按照“开挖一段、支护一段、封闭一段”的原则,每次开挖进尺为每2榀钢架(0.6 m/榀)一个循环,上下台阶长度为4.8 m,各级台阶采用平行于锚体轴线的方式进行开挖.
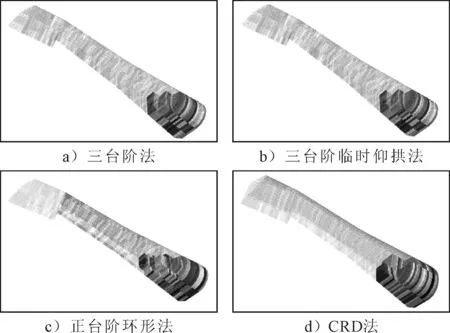
图4 不同开挖方案下的开挖支护模拟图
3.2 数值模拟结果分析
3.2.1围岩变形对比分析
通过数值方法模拟四种不同开挖方案下的隧道施工过程,得到开挖完成后的隧洞拱顶沉降数据和围岩水平位移量.不同开挖方法下的围岩最大位移见图5.
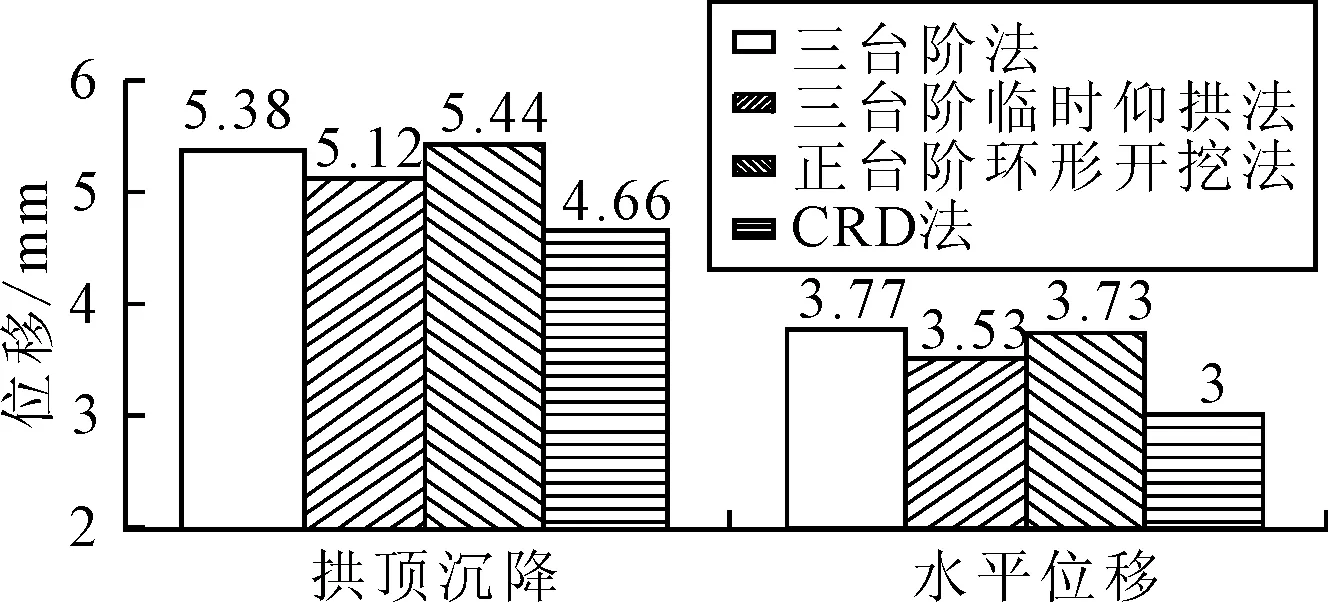
图5 不同开挖方案下的围岩水平位移图
四种开挖方案在对隧洞围岩变形的控制上差异不大,隧道拱顶沉降和水平位移量均较小,由此可见隧道锚所处山体围岩的整体稳定性较好.对于四种开挖方案而言,CRD法的拱顶沉降值最小,其次是三台阶临时仰拱法,正台阶环形开挖法最大;三台阶法、三台阶临时仰拱法和正台阶环形开挖法的拱顶沉降分别是CRD法的1.15倍、1.10倍和1.17倍.CRD法的水平位移值最小,其次是三台阶临时仰拱法,三台阶法最大;三台阶法、三台阶临时仰拱法和正台阶环形开挖法的水平位移分别是CRD法的1.26倍、1.18倍和1.24倍;对比三台阶法和三台阶临时仰拱法可知,在隧道开挖过程中设置临时仰拱,能够明显降低拱顶沉降量和水平位移,从而保证隧道锚的安全性和稳定性.
3.2.2围岩及初期支护应力对比分析
通过数值模拟得到四种不同开挖方案下隧道开挖完成后的围岩及初期支护最大应力见图6.

图6 不同开挖方案下的围岩及初期支护最大应力图
由图6a)可知:对于围岩最大拉应力,三台阶临时仰拱法最小,CRD法次之,三台阶法最大,其中三台阶法开挖的围岩最大拉应力是三台阶临时仰拱法的1.27倍;四种开挖方案下的最大围岩剪应力大小排序和围岩最大拉应力相同,仍然是三台阶临时仰拱法最小,三台阶临时仰拱法下的围岩最大剪应力是三台阶法下的72.3%;就围岩最大压应力而言,四种开挖方案在数值上差距相对较大,CRD法最小,三台阶临时仰拱法次之,其中三台阶法是CRD法的1.24倍,三台阶临时仰拱法是三台阶法的82.4%.
因为支护荷载的来源为隧道围岩变形,而围岩变形量的大小是围岩荷载与支护抗力相平衡的结果[10].因此初期支护最大应力则与围岩所受最大应力的排序不同,由图6b)可知:三台阶临时仰拱法的初期支护所受应力最大,该方案下初期支护的最大拉应力为10.33 MPa,最大压应力为9.6 MPa.除CRD法外的三种开挖方案初期支护应力相差不大,CRD法得益于其复杂的施工工艺,将隧道开挖断面划分为较小的开挖断面后分部开挖,该方案增加了大量临时支护结构,各部分封闭成环的时间变短,且支护刚度大,因此初期支护应力相对较小.
3.2.3围岩塑性区对比分析
由于塑性区主要分布在隧道锚洞的周围,而地表和内部岩体较少,故仅对比锚洞周围的塑性区分布.FLAC3D中采用now表示现在该区域内的单元处于屈服面上,past表示该区域内的单元过去处于屈服面上,而现在降到屈服面以下.因此在分析实际工程的塑性区时,重点关注的是处于now状态的屈服区域,只有这些单元才可能使模型发生破坏.
塑性区主要分布在锚洞的中后段部分,且主要沿洞周分布,两侧壁和拱部塑性区多于底板部位.开挖完成后的塑性区大部分都处于past状态,而now状态的塑性区只有局部很小的范围,这些塑性区主要分布在锚塞体段的拱脚和后锚室的端墙,即:四种开挖方案下开挖完成后的岩体大部分都处于弹性变形阶段,只有极小部分区域现在处于剪切屈服状态,对隧道锚的安全稳定基本没有影响.
4 结 论
1) 利用层次权重决策分析法,对伍家岗长江大桥北岸隧道锚开挖进行了分析,当目标指标着重于沉降变形和工程造价时,三台阶临时仰拱法开挖最优.
2) 采用FLAC3D数值分析软件,分别对四种开挖方案下的隧道锚进行单独建模,分析结果为:从控制隧道锚围岩变形和塑性区发展考虑,CRD法和三台阶临时仰拱法较优.
3) 层次权重决策分析法结论与数值计算结果一致,说明在隧道锚开挖方案选择上,层次权重决策分析法能够提供比较强的科学指导意义.
4) 在软岩浅埋隧道锚开挖方案选择上,将层次权重决策分析法和FLAC3D软件结合,能够为实际工程提供多维度的科学意见,将更好地指导隧道锚施工开挖.

