基于特征筛选BP神经网络的天然气需求量预测

佟 敏 陈忠源 党 乐 崔亚茹 马善为 李 凯

（1.国网内蒙古东部电力有限公司电力科学研究院，呼和浩特 010020；2.华北电力大学生物质发电成套设备国家工程实验室，北京 102206）

0 引言

我国天然气能源生产和消费一直处于增长状态［1］。维持天然气的稳定安全供应，首先需要准确预测天然气的需求量。传统天然气需求预测方法，主要基于天然气的历史使用情况构建模型，包括回归分析预测法、时间序列预测法、灰色模型预测法以及各种模型组合预测方法［2-5］。这些模型可以较好的预测天然气长期稳定发展，但由于模型仅仅是基于时间因素的天然气需求分析，没有分析其它因素对于天然气需求影响，特别是对于突发事件引起的天然气需求剧烈变化，模型的稳定性和准确性难以保证。近年来，随着计算机和数学理论的发展，人工智能在能源需求预测表现出良好的效果，基于人工神经网络天然气预测受到学者们的关注［6］。罗东坤等［7］通过附加动量法改进的BP神经网络对我国的天然气需求进行建模和预测，结果表明该方法对天然气的短中期预测具有较好的适用性。冯雪等［8］基于RBF 神经网络提出了针对我国天然气需求预测的非线性集成模型，预测结果表明该模型预测精度高、稳定性强。邹绍辉等［9］报道了基于DDE-BAG算法的人工智能混合优化方法，结果表明该方法具有极佳的全局和局部最优搜索能力以及较快的收敛速度，对于天然气需求的中短期预测具有极高的可信度。

虽然目前在天然气需求预测上，基于机器学习的神经网络算法已取得了较好的结果，但目前的神经网络算法的研究多数集中于算法的优化。实际上，天然气需求预测结果的好坏除了受神经网络模型算法的影响，其很大程度也取决于训练样本即天然气需求影响因素。陶阳威等［10］对中国能源需求的影响因素进行了定性分析，确定了国民生产总值（GDP）、城镇人口比例、第二产业贡献率、能源生产总量、煤炭消费比例、能源加工转化率和消费水平七个因素是影响能源需求的关键因素。叶倩等［11］将天然气需求的影响因素归为四类，经济因素（GDP、工业产值、天然气价格等）、人口因素（总人口数和户数、天然气用气人口和户数等）、限制类因素（能源结构、天然气产量等）和发展类因素（城镇化率、燃气普及率、燃气投资额等）。以上研究表明影响天然气需求的因素很多，然而目前多数神经网络模型对这些因素的选取仅仅依赖于定性分析，没有理论依据，影响了神经网络预测精度。此外，不加限制的将主观判断的影响因素作为训练样本参数，不仅增加了神经网络建模训练难度，同时会使模型学习了大量无效干扰信息，反而降低预测准确性。因此，有必要找到一种天然气影响因素筛选方法，从而获得天然气需求值的关键影响因素，进而优化神经网络模型。目前已有学者提出了一些特征因素筛选方法，主要有灰色关联度法（GRA）［12-13］、平均影响值法（MIV）［14-15］和主成分分析法（PCA）［16-17］等，但是相关研究没有指出其在天然气需求值预测方面的适用性。基于此，首先通过定性分析获得天然气需求影响因素，构建BP 神经网络模型，然后通过GRA 法、MIV 法和PCA 法对选取的因素进行特征筛选，重新建立神经网络模型进行预测评价，从而获得天然气需求值的关键影响，优化神经网络模型，实现天然气需求的准确稳定预测。

2 研究方法

2.1 BP神经网络模型简介

BP 神经网络是一种按误差反向传播的多层前馈神经网络，目前被广泛应用于模式识别、分类和模型预测等方面。BP 神经网络通常由输入层、隐含层和输出层组成，每层神经网络包含数量不一的神经元；输入层和输出层为单层结构，其神经元数量由训练样本决定，隐含层可以设置为一层或多层，其神经元数量又称隐含层节点数，没有通用的设置方法，一般通过如下经验公式确定：

式中，q为隐含层神经元数，m为输入层神经元数，n为输出层神经元数，v为常数一般取1＜v＜10。

BP 神经网络的核心思想是梯度下降，即神经网络建模过程中，当网络输出值与其期望值不一致时，通过沿着误差梯度下降的方向调整神经网络参数，使得误差减小到可接受的范围，从而获得所需神经网络模型。

2.2 灰色关联度法

灰色关联度分析法（GRA）是判断灰色系统因素之间关联性大小的一种方法。一般而言，在一个灰色系统发展过程中，若两个因素变化趋势一致，则关联程度高，反之，则较低。所谓关联程度实质是指曲线间几何形状的相似程度，可通过以下公式所定义的关联系数ς(k)来表示：

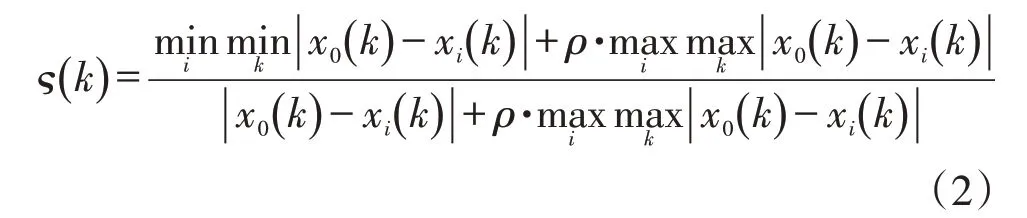
式中，x0(k)为参考序列（因变量），xi(k)为比较序列（自变量），min 和max 分别表示最小值和最大值，ρ为取值在0 和1 之间的调节系数，ς(k)为第k时刻比较序列xi与参考序列x0的关联系数。需要注意的是，由于参考序列和比较序列一般为具有不同量纲的变量，变量之间取值差异较大，为了防止大的数值变量“淹没”小的数值变量，一般需要对所有序列进行无量纲化处理。

从式（2）可以看出对于任一比较序列xi，关联系数的取值很多，信息过于分散，不利于分析，一般通过求取平均值的方式将信息进行集中处理，此平均值即为该比较序列的关联度，即式（3）。

式中，ri为关联度，N为样本总数。

2.3 平均影响值法

平均影响值法（MIA）是一种利用神经网络进行预测分析来检验输入参数对输出结果影响大小的方法，其计算过程如下：首先利用已有的原始样本P训练获得神经网络，然后将训练样本P的每一自变量在其原值的基础上分别加和减10%获得两个新的样本P1和P2，将P1和P2作为测试样本输入到已训练好的神经网络进行测试，得到测试结果A1和A2，计算A1和A2的差值即为所测试变量的影响值（IV），最后将IV 求取平均值即为测试变量的MIV值。

2.4 主成分分析法

主成分分析法（PCA）是一种数据降维方法，其目的在于将原始数据复杂参数转化为几个简单的综合指标。多数情况下，变量之间具有一定的相关性，即是变量之间反映的信息具有重叠，主成分分析通过原有变量的线性变换，删除重复变量，建立尽可能少的新变量，使得这些新变量两两之间不相关，同时确保新变量也尽可能保持原有变量信息。主成分分析的主要步骤为：①原始数据标准化，并计算相关矩阵；②计算相关矩阵的特征值及其对应的特征向量；③根据特征值大小进行排序，计算特征值占特征值总和的比例，即为特征值对应的方差贡献率；④根据累计方差贡献率确定主成分个数，计算主成分得分。

3 天然气需求预测分析

3.1 BP神经网络建模

基于BP 神经网络模型，通过查阅2019 年《中国统计年鉴》获取相关数据以建立天然气需求预测模型，相关数据如表1和表2所示。基于现有研究，选取年份、人口、城镇人口、总抚养比、GDP、第二产业、第三产业、居民消费价格指数、商品销售价格指数、能源生产总量、天然气生产量、能源消费总量和煤炭消费量等13 个因素作为天然气需求预测的主要影响因素，以每年的天然气消费量作为其需求量进行预测。在实际应用中，考虑到变量之间的量纲不同，数值差异较大，容易造成神经网络预测结果出现“过拟合”等现象，故此首先对数据进行了归一化处理，归一化公式为：

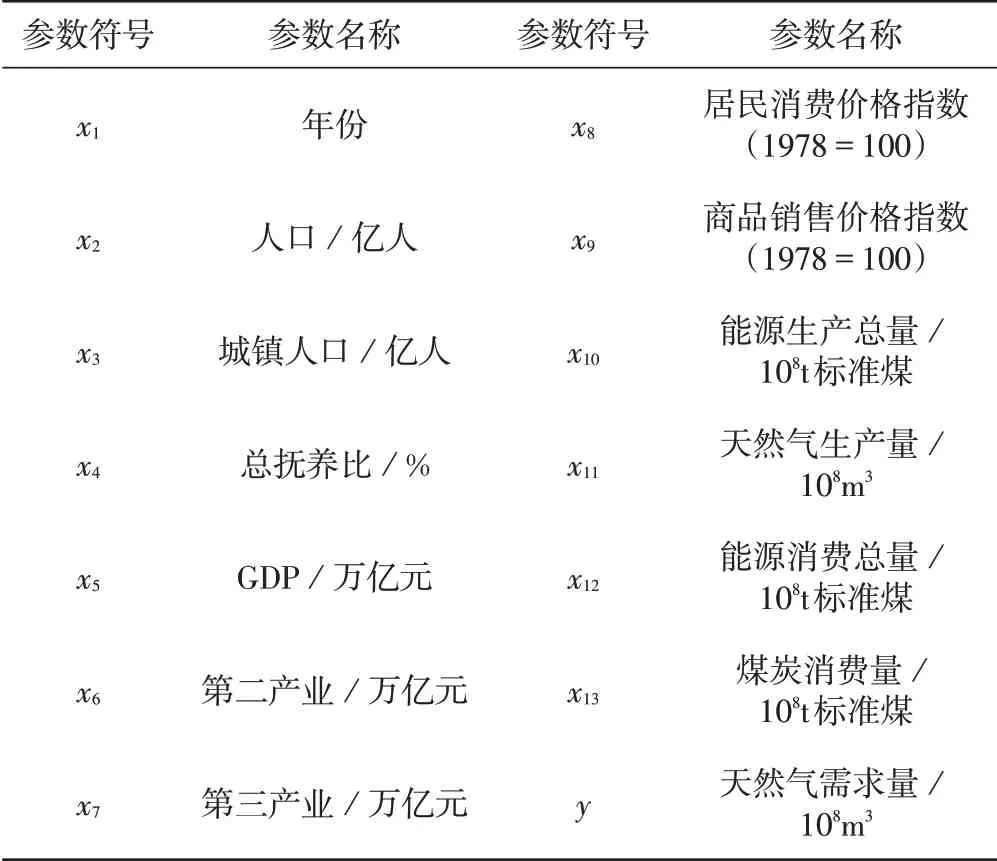
表1 参数对应表

表2 1995-2018年天然气需求量及其相关影响因素表

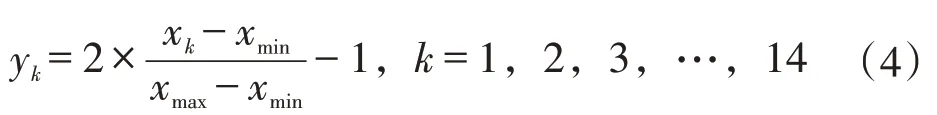
式中，xk为因素k中需要进行转化的值，xmin为因素k中的最小值，xmax为因素k中的最大值。处理后的数据样本取值区间为-1～1。采用单隐含层的BP神经网络，隐含层节点数按式（1）给出的取值范围进行多次调试，结果表明当隐含层节点数为12时，神经网络输出误差最小，最终构建的神经网络拓扑结构为13-12-1。

3.2 特征因素筛选

基于上述BP 神经网络模型，采用GRA 法、MIV法和PCA法对神经网络输入变量进行优化筛选，表3给出了输入变量的关联度和MIV 值。从表中可以看出，输入变量与天然气需求的关联度均为0.7 以上，表明这些因素均对天然气需求具有显著影响。通过MIV 法得到的天然气影响因素的MIV 值差异较大，年份和人口对于天然气需求值影响较大，而总抚养比影响最小。此外，从表中各因素的影响程度排序上看，两种方法判断因素重要程度并不一致，需要对方法适用性做进一步判断。为此，基于两种方法的判断结果进行特征筛选，GRA 法取关联度值大于0.85 为特征因素，MIV 法取相对MIV 值大于0.5 为特征因素。基于上述原则，GRA 法确定的特征因素为GDP、第二产业和天然气生产量，MIV法确定的特征因素为年份、人口和城镇人口。从筛选结果可以看出，GRA 法认为经济和天然气供应因素对天然气需求影响较大，而MIV 法认为人口因素对天然气需求影响较大。

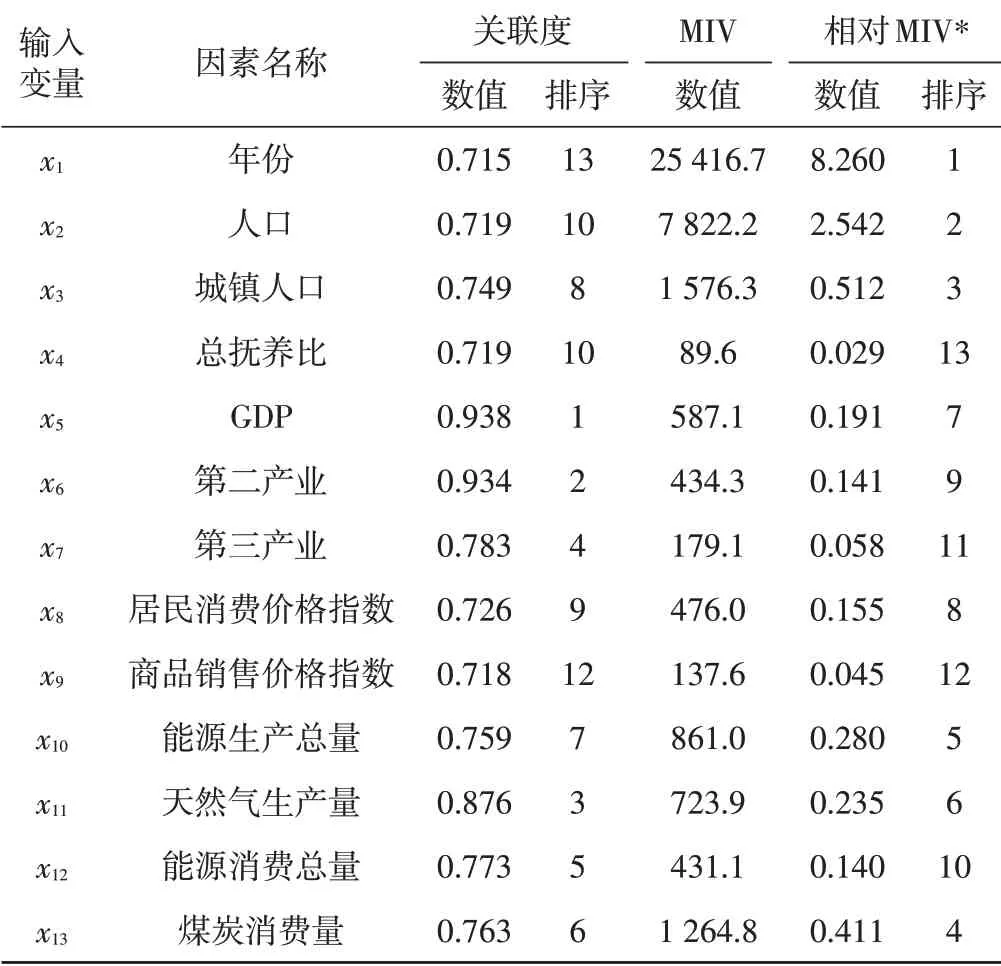
表3 输入变量的GRA和MIV分析表

类似的，对输入变量进行PCA 分析，用尽可能少的变量（主成分）来替代原始变量（因素），表4和表5分别为主成分的特征值和方差贡献率以及主成分的因子载荷矩阵，由于第九及以后主成分的特征值和方差贡献率已近似为零，故表4中没有列出。从表4可以看出，前两个主成分的方差贡献率已高达95%以上，因此本模型只需取前两个主成分即可。因子载荷矩阵主要反映原始变量指标对主成分的贡献大小，从表5 可以获得第一和第二主成分的因子载荷，由此可以获得第一和第二主成分得分计算公式5和计算公式6。从第一主成分的表达式可以看出，总抚养比对第一主成分几乎无贡献，而其余因素对第一主成分的贡献值近似相等，表明这些因素对第一主成分的影响值相当，因此第一主成分可称为“平均影响因子”。总抚养比在第二主成分中具有最高载荷，GDP对第二主成分有一定的负载荷，其余因素的载荷几乎为零，因此第二主成分可称为“总抚养比因子”。

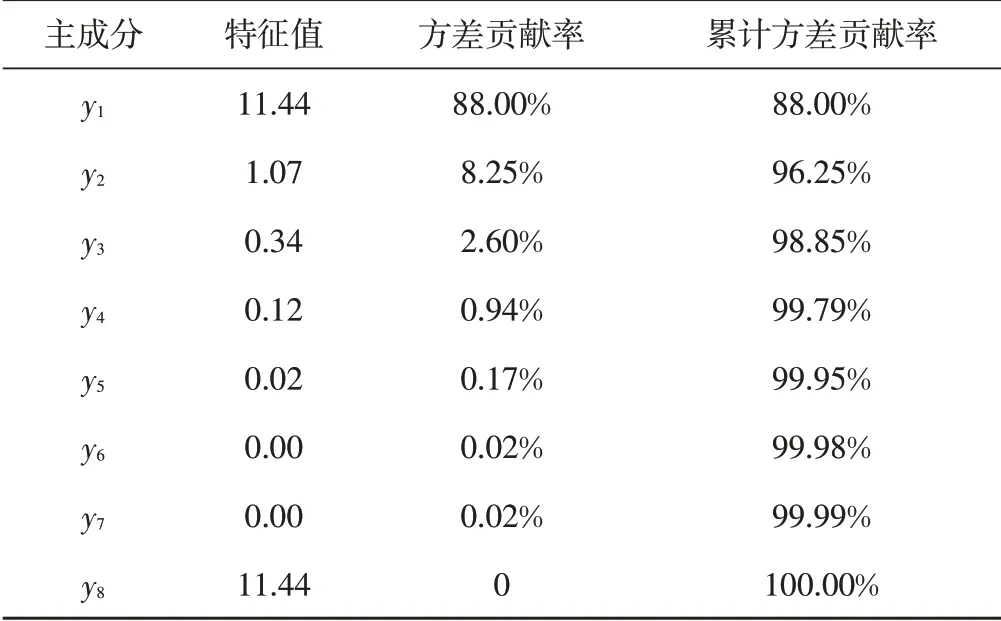
表4 主成分的特征值和方差贡献率表

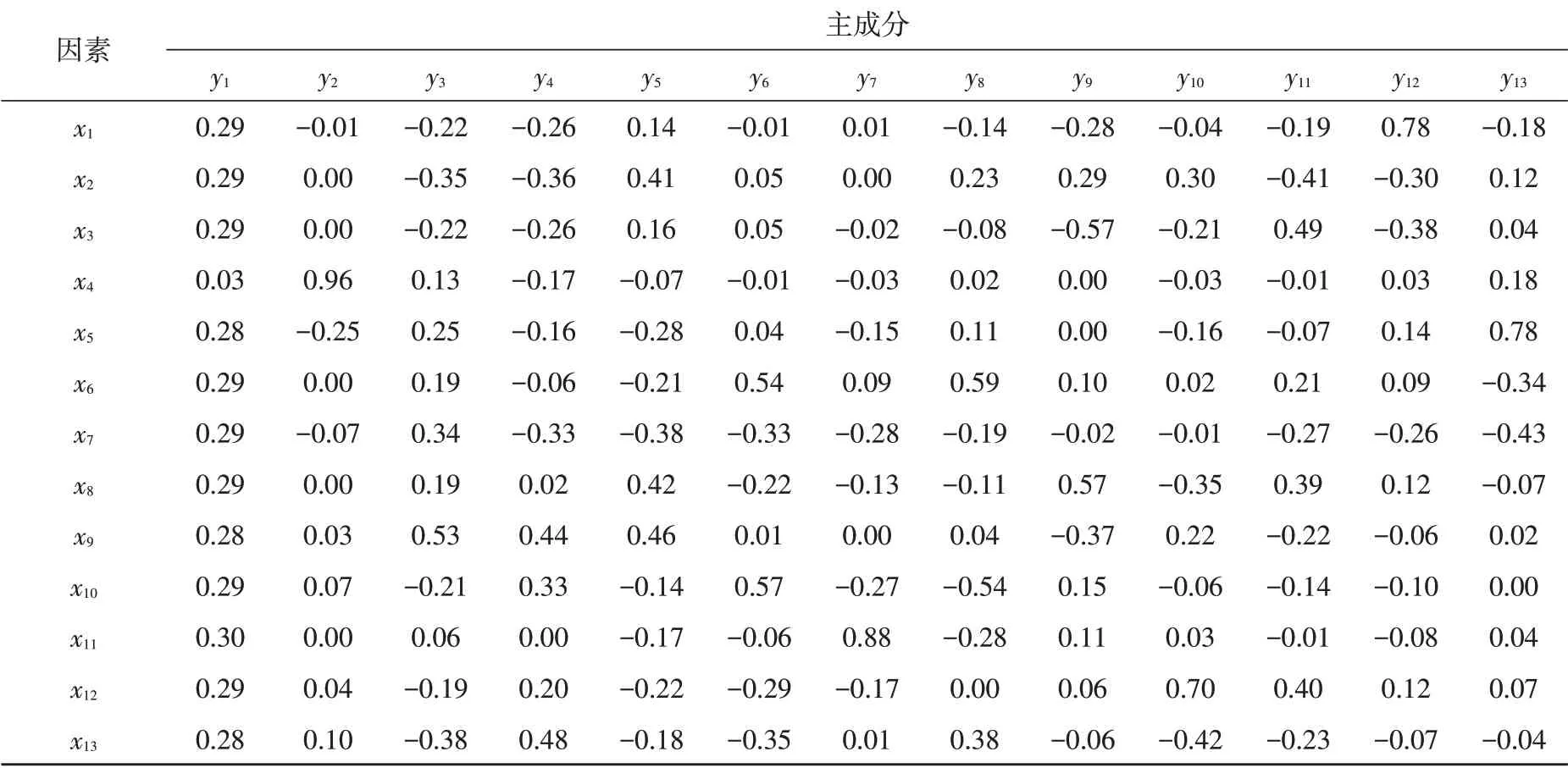
表5 主成分的因子载荷矩阵表

基于上述方法的特征筛选，GRA 法优化的神经网络拓扑结构为3-12-1，MIV 法优化的神经网络拓扑结构为3-12-1，PCA 法优化的神经网络拓扑结构为2-12-1。为了判明特征筛选对神经网络预测的影响，基于上述特征筛选后样本重新进行神经网络学习和预测，随机选取95%的原始样本作为训练样本，其余作为测试样本进行预测，测试结果如表6 所示。表6 中的对比组为未经特征筛选的BP 神经网络预测结果，可以看出经过特征筛选后，神经网络预测误差均大幅下降，MIV法相比另外两种方法效果更佳。

表6 天然气需求量预测测试表 单位：108m3

3.3 天然气需求预测分析

基于上述特征筛选后建立的BP 神经网络对2019—2025 年的天然气需求进行预测，为了分析本模型预测效果，同时采用了传统的灰色预测模型GM（1，1）［18］对天然气需求进行预测作为对比。由于PCA 法计算主成分时需用到所有的原始变量，为此需要获取预测年份的所有影响因素值。邹绍辉等［9］提出了两种获取影响因素值的方法，即曲线拟合法和情景假设法。采用情景假设对原始影响因素进行取值，即假定2019—2025 年各因素的增长率保持为2018 年相对2017 年的增长率，由此求得原始影响因素值，如表7所示。表8为四种方法对2019—2025年天然气需求的预测结果。从天然气的需求变化趋势上看，四种方法均预测我国天然气处于增长状态，这与文献报道是一致的［19-20］。从2019—2025 年的天然气需求量预测值来看，三种特征筛选BP神经网络模型的预测值相近，GM（1，1）模型虽然对于2019—2020 年的天然气需求量与神经网络法预测值较为相近，但其对后几年的天然气需求量预测值较大。从天然气的需求影响分析可知，天然气需求量主要受经济和人口的影响，经济的持续增长促进天然气需求量的增大，而人口规模直接关系天然气的使用规模，随着我国人口增长水平的下降，这促使天然气需求量增长幅度下降，通过GRA 法和MIV 法均预测至2025 年天然气需求值已趋于稳定，预计2026—2027年可到达峰值，而PCA 法预测至2025年天然气需求值增长已呈现明显的变缓趋势，按此趋势预计至2028—2029 年到达峰值。相比而言，GM（1，1）模型并没有出现明显的预测峰值，这是因为GM（1，1）只使用天然气历史需求值作为建模数据，在没有新数据进行调整更新时，其累计迭代误差会越来越大，因此只适合作为一种短期的趋势预测方法。综上所述，基于特征筛选BP神经网络模型的预测误差小、精度高，具有较好的稳定性和可靠性。

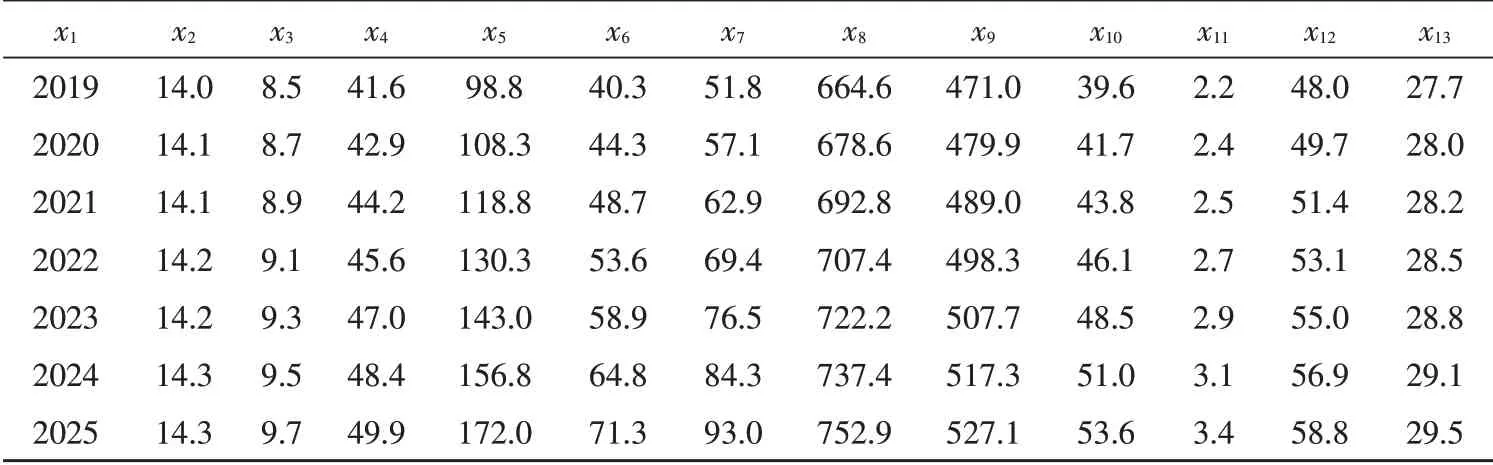
表7 2019-2025年天然气需求量预测相关影响因素表

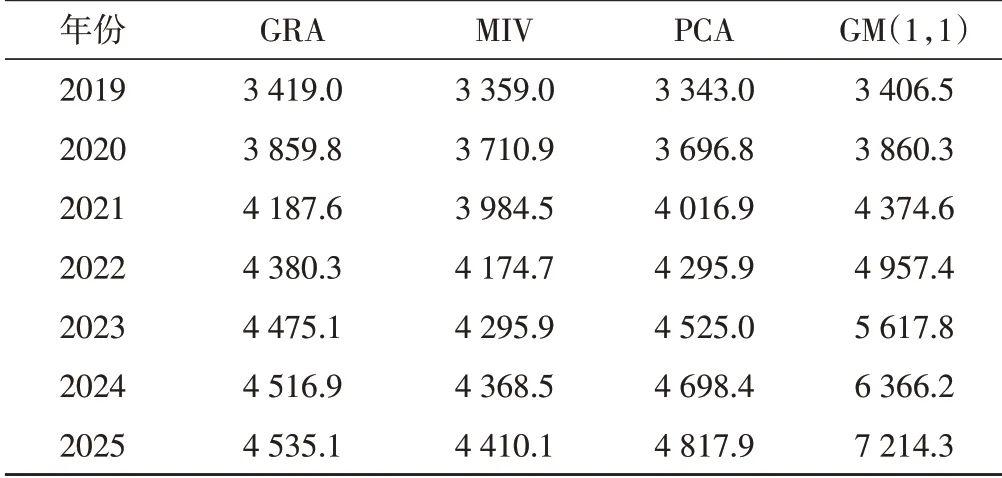
表8 2019年-2025年天然气需求量预测表 单位：108m3

4 结束语

提出了一种基于输入参数特征筛选优化的BP 神经网络天然气需求预测方法。通过实例分析发现，利用灰色关联度分析、平均影响值分析和主成分分析对天然气需求影响因素进行优化筛选，可以有效降低神经网络复杂性，提高预测精度，平均影响值法相比另外两种方法效果更佳，平均相对误差从9.077%降低至0.983%。利用特征筛选后训练所得的神经网络对2019—2025 年天然气需求进行预测，结果表明三种特征筛选神经网络模型预测的天然气需求量相近，均预测至2030 年之前天然气需求值可达峰值，相比而言灰色预测模型则没有明显的达峰趋势，只合适用于短期预测。综上所述，基于特征筛选BP神经网络模型具有较好的精度、稳定性和准确性，可用于中长期的天然气需求量预测。