北航陆士嘉实验室气动声学风洞试验研究进展
刘沛清 郭 昊
(北京航空航天大学陆士嘉实验室(航空气动声学工业和信息化部重点试验室), 100191)
0 引言
随着社会的发展,民航业对于噪声的要求逐渐提高,气动噪声成为当下飞机设计的研究热点。鉴于气动噪声的复杂机理,目前风洞试验仍然是该领域研究的重要手段,梳理当下重点风洞研究进展对未来气动噪声研究有着重要的指导意义。
欧美航空发达国家从20世纪70年代开始有步骤地开展了高品质气动声学风洞的建设,目前在尺度、性能和关键指标等方面已形成适用于基础研究、应用基础研究和工程应用研究三个层面的气动声学风洞体系。利用这些风洞群,欧美国家长期开展大型客机气动声学的基础研究、应用基础研究和工程应用研究。据不完全统计,欧洲有2 m以下量级的气动声学风洞5座,2 m~4 m量级的1座,8 m及以上量级的2座;美国有2 m以下量级的气动声学风洞4座,2 m~4 m量级的3座,8 m及以上量级的2座。典型风洞如美国NASA Langley中心LSAWT、德国DLR AWB风洞、荷兰NLR、英国南安普顿大学ISVR声学风洞、美国弗吉尼亚大学声学风洞、NASA Glenn NATR、美国佛罗里达大学声学风洞、美国海军泰勒研究中心低噪声风洞、法国CEPRA19、德国DLR NWB风洞、波音LSAF和NASA Lewis 9 ft×15 ft风洞,这些风洞主要开展基础和应用基础研究,另外还有德荷DNW LLF、法国ONERA S1MA风洞、NASA Langley 4 m×7 m风洞、NASA Ames全尺寸风洞、英宇航RAE和RTRI日本高速列车风洞,这些风洞主要开展型号风洞试验和工程应用研究。
在欧洲,空客公司利用法国ONERA中心的2 m级的气动声学风洞——CEPRA19风洞,完成了A320等客机的部件噪声机理与抑制措施的风洞试验研究;利用德国和荷兰联合建造的DNWLLF 8 m×6 m的气动声学风洞,完成了A320、A340、A380等大型客机的航空气动声学风洞试验。由于该风洞具有优良的气动声学试验能力,我国C919和CR929等机型的航空气动声学试验也在该风洞中进行。
在美国,波音公司使用美国弗吉尼亚大学1.83 m×1.83 m气动声学风洞、海军泰勒研究中心的2.4 m×2.4 m气动声学风洞,开展了波音737等大型客机气动声学机理与基础问题研究;利用NASAGlenn研究中心的4.6 m×2.4 m气动声学风洞和经过声学改造后的NASA Lewis研究中心的4.57 m×2.74 m低速风洞等,完成了波音737等大型客机部件气动噪声测试、噪声抑制措施等应用基础研究,为向工程应用推广提供了强有力的支持;利用经过气动声学改造的NASA Langley 4 m×7 m低速风洞、NASA Ames 24 m×12 m低速风洞等,完成了波音737等大型客机气动噪声的生产型风洞试验。
目前国内航空气动声学风洞数量偏少,我国已建和在建的航空气动声学风洞包括:29基地8 m×6 m和5.5 m×4 m的生产型气动声学风洞,中国空气动力研究院8 m×6 m和2 m×1.5 m生产型和研究型风洞,北京航空航天大学4 m×3 m、1 m×1 m和0.2 m×0.2 m的研究型风洞等。这些大型气动声学风洞主要承担大型客机部件或全机的生产型气动声学风洞试验。
在大型客机型号与生产研制中,从实际工程问题中凝练基本科学问题,首先在研究型风洞中进行气动声学一般性或部件的机理基础问题研究,然后在应用基础研究型风洞中进行与部件密切相关的气动噪声机理和降噪措施研究,最后在型号与生产研制风洞中进行与全机密切相关的气动噪声工程技术问题研究,这样使得我国气动声学的基础研究和工程应用研究紧密结合,可以形成以基础研究为支撑,以应用基础研究为纽带,以型号与生产研制为目标的整体格局。
近年来,围绕大型客机的机体噪声产生机理及降噪原理,北京航空航天大学陆士嘉实验室也在气动声学风洞实验基础研究方面开展了相关研究。本文介绍了主要试验研究成果,并结合试验室配套的试验测量装置和模型介绍,为同行提供参考。
1 试验装置和方法
1.1 试验风洞及测量装置
北航陆士嘉实验室现有气动声学基础研究型风洞两座,其基本型式为单回流式气动声学风洞,即D5风洞和D7风洞。
D5风洞是一座1 m量级的回流式气动声学风洞,具有低湍流度和低噪声的特点,风洞喷口截面尺寸为1 m×1 m。风洞包括两个试验段,开口试验段长度为2 m,最大风速为80 m/s;闭口试验段长度为2.5 m,最大风速为100 m/s。试验模型的最大Re数可以达到106量级。风洞试验段中心最大来流湍流度为0.08%。为了降低风洞背景噪声以及噪声反射对模型噪声测试的影响,D5气动声学风洞的试验段采用了多种消声设计。如图1所示,在D5风洞试验段外侧建有消声室,消声室的长度为6 m,宽度为6 m,高度为7 m。消声室的外墙是由40 cm厚的CAIA-L低频吸声隔声板制成,以达到消除消声室内的声波反射和隔绝消声室外噪声的目的。同时,风洞内部也采用了消声设计,风洞内壁使用单通道消声器并联的方式进行消声,而风洞动力段则是使用微穿孔板消声技术,微穿孔板内的空气柱振动可以有效地消除中、低频的噪声。风洞的消声设计可以吸收99%以上的反射噪声,用于模拟自由声场环境,并满足声传播的平方反比规律。自由声场的低频截止频率为200 Hz。当来流速度为80 m/s时,在距离风洞中心轴线1.5 m远的地方进行背景噪声的测量,其总声压级低于85 dB(A),小于等于同量级气动声学风洞的背景噪声幅值。

图1 D5风洞气动声学风洞
D7风洞是北航在建的4 m×3 m低湍流度气动声学风洞(BHAW)的1∶15缩比模型,是一座低湍流度低噪声的低速回流风洞。动力段采用了低噪声风扇设计和微穿孔板消声器,洞壁配有声衬降噪技术。试验段为开口,长500 mm,其截面尺寸为200 mm×200 mm,射流核心区湍流度小于0.1%,测试风速范围为0.1 m/s~40 m/s。试验段外为一座小型的消声室,如图2所示,消声室的长、宽、高分别为1.4 m、1.6 m和1.9 m。在设计风速50 m/s下场外噪声为72 dBA。

图2 D7气动声学风洞
声学试验中用到的麦克风包括测试远场噪声的自由场传声器和测量近场噪声的壁面麦克风。自由场传声器的型号为丹麦Brüel & Kjær公司的4189型1/2英寸自由场传声器,如图3(a)所示。这是一种专为高精度自由场测量设计的通用型传声器,配有CCLD和传统两种前置放大器,几乎适用于所有远场噪声测量场景。该传声器的敏感度为50 mV/Pa,声压级测量动态范围为14.6 dB~146 dB,有效测量频率为6.3 Hz~20 000 Hz,完全能满足试验研究需求。壁面麦克风采用丹麦G.R.A.S.公司的40LS 1/4″ CCP高精度壁面麦克风,如图3(b)所示。其内部配有集成的CCP前置放大器,并随附有内置的TEDS芯片。麦克风厚度只有2.5 mm,直径也只有15 mm,由于其轻巧的特性因此可以直接贴附于模型表面进行测量。其敏感度为1.8 mV/Pa,声压级测量动态范围为46 dB~167 dB,有效测量频率为5 Hz~70 000 Hz,能满足试验研究需求。麦克风测试的声压数据传输到电脑上需要借助采集器,本文研究中采用Brüel & Kjær公司的LAN-XI 3053型高密度12通道输入模块,如图3(c)所示。在本文的所有声学试验中,麦克风的采样频率均为65 536 Hz。在对采样得到的声压信号进行快速傅里叶变换的过程中为光滑得到频谱曲线和防止漏能,采用了Tukey-Hanning窗函数(其中余弦窗比例为0.25),并使用了分块平均的方法,每两个分块之间的重叠率为50%。

(a) Brüel & Kjær 4189型1/2英寸自由场传声器

(b) G.R.A.S.40LS 1/4″ CCP高精度壁面麦克风

(c) Brüel & Kjær LAN-XI 3053型高密度12通道输入模块图3 声学采集系统
1.2 试验模型
增升装置试验所选择的模型,主要有两套。第一套模型选择BANC(Benchmark problems for Airframe Noise Computations)标准模型,即常规、无后掠的30P30N翼型,翼型的干净弦长c=0.457 2 m。在试验前,翼型的三个展向截面共布置了150个测压孔,用于测量翼型表面的静压分布,如图4所示。

(a) 30P30N实验模型示意图

(b) 模型表面压力测量孔分布示意图图4 30P30N实验模型及表面压力测量孔分布示意
在此基础上,利用另外一套模型研究了三种典型的前缘增升装置构型的低频噪声特性。该模型前缘增升装置分别为前缘缝翼、前缘克鲁格襟翼和前缘下垂构型,后缘增升装置为后缘铰链襟翼。模型由五个部分组成,如图5所示,包含前缘部件、主翼前缘部件、主翼中段部件、主翼后缘部件以及后缘襟翼部件。增升构型模型的展长为1 m,与风洞的截面长度相同,前、后缘增升装置收起后的干净翼型弦长C为0.4 m。其中,前缘缝翼弦长为17.7%C,后缘铰链襟翼弦长为18%C,干净翼型的最大厚度为11.1%C。

(a) 前缘缝翼模型

(b) 前缘克鲁格襟翼模型

(c) 前缘下垂模型图5 不同前缘的增升装置模型示意图
为了同时进行流场和远场气动噪声的测量,对D5气动声学风洞的闭口段试验段在吸力面和压力面采取不同的措施。参照Virginia大学的做法,利用Kevalr布的透声性能,两侧均采用了Kevalr布。但是由于高升力构型吸力面负压太大,在吸力面的Kevlar布用一层穿孔板进行支撑。整个试验构型如图6所示。

图6 三段翼翼型构型在Kevlar闭口试验段的布置
起落架试验所选择的模型为1/2缩比的LAGOON项目简化前起落架模型,主要包括轮胎、连接杆和支柱三个部件,其中轮胎直径D=0.15 m。轮胎、连接杆和支柱的迎风表面都贴有粗糙带进行人工转捩,粗糙带位置和尺寸,以及传感器的方位角与LAGOON项目完全相同。具体试验布置如图7所示。

图7 简化前起落架试验布置图
2 多段翼型气动噪声机理实验研究
2.1 实验研究概述
陆士嘉实验室围绕增升装置的多种构型展开研究,包含30P30N的干净构型、二段翼构型以及三段翼构型,以及某三段翼的前缘缝翼、前缘下垂和前缘克鲁格构型进行气动噪声机理和降噪技术的试验研究。试验主要是在D5气动声学风洞中进行的,试验测量包括压力扫描仪测量翼型表面压力分布,热线风速仪测量流场的速度场,远场声学探头和麦克风阵列研究气动噪声特性,如远场噪声谱特性和声源定位。研究使用了小波变换的方法对多重离散噪声峰值现象进行了小波分析。还借助数值模拟的方法对流场的信息进行补充分析,对表面压力分布和表面摩擦系数分布、空间流场的特征等进行计算,进一步通过流场的分析揭示翼型的气动噪声机理,如图8所示。

图8 不同试验段下30P30N表面压力测量图[5]
通过30P30N标准模型气动声学试验流场和声场两个方面多种结果的验证,发现试验段的吸力面侧壁使用内侧Kevlar布用透明的钓鱼线固定在外侧穿孔板上,而压力面只有一层Kevlar布的声学试验段设计不仅可以克服高升力构型吸力面负压太大,还能减少压力面测量的声学损失和干扰,同时解决了固壁闭口试验段和开口试验段的局限性,可以看作是气动闭口和声学开口的新型试验段。这种改造后的声学试验段不仅能可靠准确地在没有流动干扰的稳定环境下进行多段翼型气动特性测量,而且能在具有良好声音穿透性的近似无声反射的环境下进行多段翼型声场特性测量,为在小尺寸风洞中进行相对较大较复杂模型的气动声学试验提供有效的基础。这种利用Kevlar布和穿孔板的侧壁方案,在满足气动相似的基础上,实现30P30N增升装置模型的气动声学远场测量方案得到AIAA航空航天2017年度综述的评价。
首先利用完全收起前缘缝翼和后缘襟翼的30P30N干净翼型开展单段翼气动噪声实验研究,再在30P30N标模的研究基础上,分别针对带腔体的前缘缝翼和前缘克鲁格缝翼两类增升构型及不带腔体的前缘下垂构型的声场特性以及流场特性开展研究。
2.2 单段翼型远场噪声特性
翼型尾缘离散噪声曾被认为是由卡门涡街在湍流尾迹周期性脱落导致的,但是实际中离散声并不会出现在全尺寸飞机上,而只在一定雷诺数的翼型模型实验中出现。Paterson利用NACA0012和NACA0018翼型进行了大量不同工况的远场噪声实验研究,发现出现离散噪声时翼型的一面至少存在层流边界层,此时随来流速度增大而阶梯上升的主峰噪声频率与来流速度的0.8次方和1.5次方分别存在一定范围拟合和整体拟合的线性关系。Tam根据涡脱落的频率特性以及阶梯现象在Paterson的实验数据分析反驳了尾缘离散噪声的涡脱落机理解释,并提出类似腔声自激振荡的自反馈环理论。Fink进一步补充了Tam的理论,认为翼型尾缘处压力面内的Tollmien-Schlichting(T-S)波是加强反馈的原因。Brooks发现翼型尾缘处的层流脱落涡会产生尖频噪声。Arbey和Bataille则对三种不同厚度NACA0012翼型在0°迎角下分别在相同雷诺数和相同压力梯度情况下进行了实验,发现了离散噪声实际上是以主频和一系列等间隔的离散频率(旁瓣)构成,并验证了Tam的声反馈环理论。Lowson等发现翼型离散噪声的强度与翼型压力面的分离泡大小有关,且只有在一定的雷诺数范围内产生。Nash等在不同实验工况下均观察到翼型压力面会出现一个回流区。Mcalpine等认为翼型尾缘涡脱落与圆柱绕流之后的涡脱落类似。除了风洞实验研究,针对翼型尾缘的离散噪声的计算工作也在逐步进行。Desquesnes对NACA0012进行了二维计算仿真,认为翼型吸力面上也存在一个反馈环并通过模态调节影响压力面上反馈环结果。李伟鹏通过二维DNS计算认为反馈机制不仅在压力面上存在,也在吸力面上存在。Jones和Sanberg通过二维DNS计算认为单一的T-S波计算结果的频率并不足以匹配主频,认为整个翼型的流动失稳导致了尾缘离散声。Tam和Ju根据他们的数值计算结果提出了尾缘噪声基于尾迹区靠近上流边界层出的Kelvin-Helmholtz不稳定性。最近,Pröbsting等通过PIV技术结合小波分析处理NACA0012翼型尾缘处的流动速度脉动、表面压力脉动和噪声时间信号,验证了反馈环假说下尾缘周期性对流失稳引发的压力脉动是声波向来流方向传播的原因,并揭示了主瓣和旁瓣的振幅调制机制,验证了Desquesnes的翼型吸力面自反馈环的计算结果。
对于干净构型的气动噪声问题已经做了大量的研究,而对于三段翼型在前缘缝翼和后缘襟翼都完全收起的这一更接近真实应用的干净构型的气动噪声却缺少深入研究。
由于30P30N模型设计之初就是打开前缘缝翼和后缘襟翼的三段型的模型,并不是从一个真正意义上的干净构型抠出的前缘缝翼和后缘襟翼,所以在把前缘缝翼和后缘襟翼收起来后,与主翼不能完全地契合,前后上下四个位置形成了一些小台阶和缝隙,具体情况如图9所示。
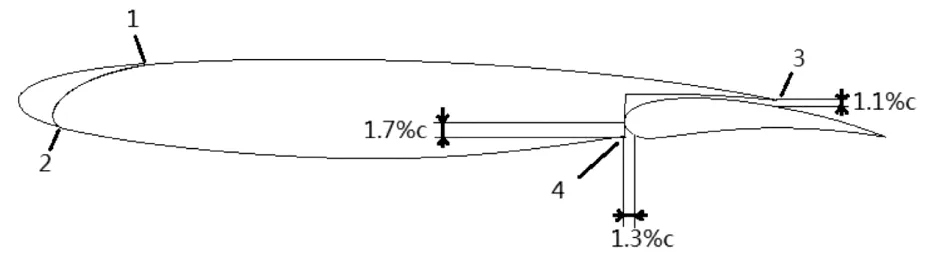
图9 收起的干净构型的缝隙和台阶示意图
通过对完全收起前缘缝翼和后缘襟翼的干净翼型的气动噪声特性研究,发现干净构型远场气动噪声随迎角的变化规律和马赫数相似律,远场噪声谱中出现的低频离散峰值,如图10所示,主要来源于干净构型下翼面与收起的襟翼之间的缝隙附近边界层中不稳定的T-S波与分离泡的压力脉动相耦合所形成的反馈回路。如图11所示,进一步使用小波分析发现波系数云图中只显示多重离散峰值的一个主频,其他二级频率是由主频附近的压力脉动的振幅调制现象产生的。

图10 单段翼型远场噪声谱[5]

图11 离散频率小波系数的功率谱[5]
2.3 30P30N标模远场噪声特性
由于多段翼型自身的结构复杂性决定了其流动复杂性,二维三段翼型绕流中可能出现的各种流动物理现象包括:层流气泡、边界层转捩、激波/边界层干扰、分离的凹角流动、剪切层转捩、边界层分离、尾迹/边界层掺混等,而这些复杂的流场特性进一步导致多段翼增升构型的各种噪声的产生。而前缘增升装置,由于其附近的流动速度较高,流场特征就更为复杂。如图12所示,在前缘缝翼下尾缘尖端处流动发生分离,形成一定厚度的剪切层,由于Kelvin-Helmholtz不稳定的影响,自由剪切层逐渐破碎为离散涡结构并向下游发展,最后再附于缝翼压力面靠近尾缘处的壁面。一部分涡系结构进入凹槽空腔内的“低速回流区”,不同尺度和强度的涡与壁面相互作用,回流在下尾缘尖端处影响新生剪切层的产生,形成回流反馈机制。另一部分涡系结构继续向下游发展,由于剪切层外部流动的作用被加速,使得流动从再附区到尾缘处发生了强烈的变形和扭曲,最终与上尾缘附近的流动相互作用发生尾缘涡脱落现象。前缘缝翼气动噪声可以分为三种主要的噪声类型,前缘缝翼凹腔内的非定常流动会产生中、低宽频湍流噪声,缝翼下尾缘边界层分离以及剪切层流动是低频离散噪声产生的原因,而尾缘涡脱落则导致高频驼峰噪声的产生。

图12 多段翼附近流动示意图
关于前缘缝翼所产生的中、低频多重离散噪声机理的观点主要包括两种。第一种观点是缝翼凹腔内的流-声反馈机制。与传统方腔的自激振荡噪声机制相似,在缝翼的下尾缘附近剪切层内由于Kelvin-Helmholtz不稳定性,会产生一系列非定常的涡结构,这些涡沿着剪切层向缝翼上尾缘运动,并流动再附于缝翼上尾缘的压力面。由于涡结构与固壁的相互作用,高强度的噪声因而产生,并向外辐射。辐射的声波回传到缝翼的下尾缘,继而再次激发下尾缘处的Kelvin-Helmholtz不稳定性,最终形成流动与声波的相互激励以及反馈。
Kolb等分别研究了前缘缝翼展开与否,缝翼凹腔被填充后,以及添加尾缘挡片后的远场噪声及流动特性。结果表明,缝翼凹腔流动所产生的低频离散噪声频率与Rossiter推导出的传统空腔自激振荡经验公式所预测的频率一致,缝翼凹腔内的噪声机制与传统空腔内的噪声机制相似。Terracol等通过实验测量了缝翼远场噪声以及翼型表面压力脉动,并数值模拟了增升构型流场特性。通过比较声场和流场特性发现,离散噪声成分与剪切层和声波之间的反馈回路有关。然而,由于缝翼凹腔的形状并不规则,Terracol等基于实验与数值结果改进了Rossiter所提出的频率预测公式,将剪切层内涡运动时间与声波传播时间进行耦合,并引入改进后的公式。实验所得到的离散噪声频率与改进后公式预测的频率更加吻合,而且剪切层内的流动特性与低频离散噪声特性之间具有密切的关系。Khorrami等通过非定常数值模拟以及声学分析了缝翼下尾缘附近的自由剪切层特性后发现,在自由剪切层内存在着大尺度、低频率的振荡,而这种振荡会因为Kelvin-Helmholtz不稳定性而加强。Kelvin-Helmholtz不稳定性是剪切层卷起并形成不同尺度涡结构的重要机制。Jenkins等利用PIV(Particle Image Velocimetry)测试手段,捕捉缝翼凹腔内流动速度以及涡量的平均值与脉动值,分析了剪切层内涡的演变过程,提出涡结构在近壁区域的冲击和变形是低频离散噪声产生的主要原因。Nelson等针对涡声相互转化进行研究,研究结果表明剪切层与固壁的相互作用会产生涡能量向声能量的转化。漩涡流动会产生声波,无论是在冲击过程,还是触发空腔或隧道(亥姆霍兹共振器中的驻波,包括深度、长度、展向模态)中的声共振模态的过程中都会发生。而涡在冲击过程中的变形与加速是造成涡能向声能转化的基本原因。同样,声能也可以向涡能转化。剪切层内的不稳定性会吸收声能,将一部分的声能量转化成涡脱落的动能。König等对前缘缝翼进行混合LES/CAA(Large Eddy Simulation/Computational Aeroacoustics)数值模拟,结果表明缝翼声场中的低频离散成分与剪切层-固壁的相互作用有关。之后,通过将声场结果与LES模拟的流场结果进行相关分析,确定了缝道内产生的压力脉动在缝翼下尾缘和主翼表面之间具有一种流-声反馈机制。
本文对30P30N多段翼标模的气动噪声特性进行研究。实验表明:当前缘缝翼完全打开时,在高频段,低迎角工况下会出现一个由前缘缝翼尾缘涡脱落引起的峰值噪声。如图13所示,这些低频离散峰值的频率与Terracol公式的预测值吻合较好,在D5风洞得到了实验验证。而且通过小波分析,发现前缘缝翼凹槽内辐射出的多重峰值噪声符合空腔噪声自激振荡现象的主模态转换和模态切换机制。图14给出了前缘缝翼远场气动噪声随迎角的变化规律和马赫数相似律,实验测量的30P30N三段翼型的远场噪声基本上满足Ma数的4.5次幂律,与其他人的结果基本吻合。

图13 三段翼型远场噪声谱[4]

图14 Ma数4.5次幂律无量纲能谱密度随St数变化[4]
在此基础上分别研究了改变30P30N模型前缘缝翼及后缘襟翼偏角对远场气动噪声的影响,发现在前缘缝翼偏角较大时远场噪声谱中在低频1 000 Hz~5 000 Hz范围内会出现离散峰值强度随着前缘缝翼偏角的逐渐减小而逐渐减弱直至消失的情况,如图15所示。这是因为前缘缝翼偏角的减小导致前缘缝翼压力面靠近尾缘处的剪切层再附位置不断前移,前缘凹槽内的回流区尺寸逐渐变小,剪切层的速度也逐渐下降,分离泡逐渐减小并且形状发生变化,导致凹腔来流速度及特征尺寸均发生变化。
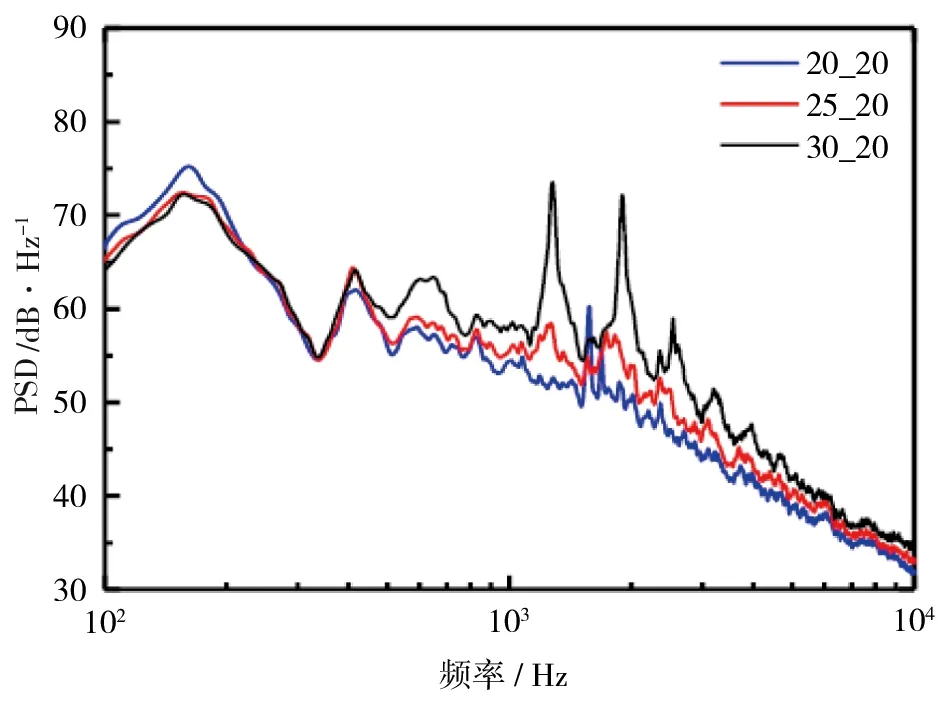
图15 不同前缘缝翼偏角下远场噪声谱[15]
通过对多段翼型后缘襟翼的气动噪声特性进行研究,发现当后缘襟翼的偏角较小时,远场噪声谱会在低频1 000 Hz~3 000 Hz范围内出现离散峰值,这些低频离散峰值主要来源于襟翼前缘和主翼下表面尾缘形成的凹槽,气流流过主翼下表面尾缘处产生的脱落涡会沿流向向下游运动撞击到襟翼前缘,产生压力脉动向上游传递,传递出的压力波到达主翼下尾缘分离处,与主翼下表面尾缘分离处新产生的脱落涡相耦合,形成一个类似空腔的反馈回路,激发出远场噪声频谱中的低频离散峰值。随着后缘襟翼偏角的增加,这些离散峰值的强度会逐渐减弱,当后缘襟翼的偏角增加到一定程度后,襟翼与主翼之间的缝道有气流流过,空腔流动消失,耦合作用被破坏,远场噪声谱中的离散峰值消失,声谱表现出宽带谱特性,如图16所示。

(a)小偏角实验结果

(b)大偏角实验结果 图16 不同偏角后缘襟翼的远场噪声谱[15]
2.4 前缘缝翼自激振荡噪声机理研究
如前所述,前缘缝翼气动噪声中的多重离散噪声源于缝翼凹腔的自激振荡机制,本节重点针对此现象开展研究。如图17所示,通过引入前缘增升装置凹腔当地的流动参数,改进了前缘增升装置凹腔内自激振荡特征频率的预测公式。同时,基于改进后的特征频率预测公式,进一步提出参与凹腔自激振荡主模态选择的流场参数,分别为:缝翼下尾缘分离点沿自由剪切层到上尾缘再附点的长度、缝翼下尾缘处分离边界层的厚度以及自由剪切层内对流速度与分离边界层内最大速度的比值。其中,对于前缘缝翼凹腔而言,缝翼下尾缘分离边界层厚度是前缘缝翼凹腔自激振荡主模态选择的决定性因素。如图18所示,需要综合考虑三个参与主模态选择的流场参数的变化率。如图19和20所示,分别验证了不同来流速度及迎角对缝翼凹腔内的自激振荡离散噪声主模态选择的依赖关系。
无缝缝翼被认为是传统前缘缝翼的降噪构型。无缝缝翼是指将前缘缝翼与主翼之间的缝道封闭,使用的方法包括:使用缝道遮挡板使得缝道内的流动被阻挡、前缘缝翼变形使得缝道宽度变为0,等等。本文使用的方法是将前缘缝翼沿着主翼弦线方向平移,将缝道宽度逐渐降到0。

图17 参与凹腔噪声特征频率预测的流场参数示意图

图18 不同来流迎角下流场参数值[16]

图19 来流速度对缝翼凹腔自激振荡主模态的影响[16]

图20 来流迎角对缝翼凹腔自激振荡主模态的影响[16]
如图21和22所示,前缘缝翼缝道的闭合确实可以有效降低增升构型的噪声辐射量,并且降噪效果十分明显。前缘缝翼凹腔内自激振荡主模态的改变同样也会影响增升构型的总体噪声辐射量。如图23所示,在前缘缝翼凹腔自激振荡主模态选择过程中,是决定性因素,其变化趋势会直接影响主振荡的切换方向。
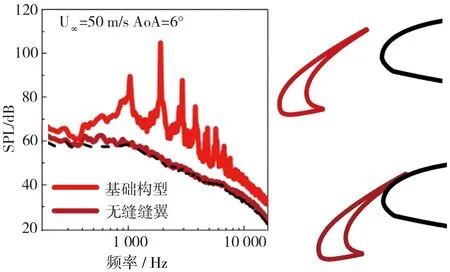
图21 来流速度50 m/s迎角6°时前缘缝翼缝道闭合前/后远场噪声频谱图[16]

图22 来流速度50 m/s时前缘缝翼缝道闭合前/后总声压级对比[16]

图23 来流迎角对缝翼凹腔自激振荡主模态的影响[16]
2.5 前缘克鲁格襟翼远场噪声机理研究
对于前缘克鲁格襟翼构型而言(如图24所示),其前缘克鲁格襟翼凹腔以及克鲁格折叠腔都会产生低频的离散噪声,噪声产生机理均为腔体内的自激振荡现象,如图25所示。由于缝道流动的加速,前缘克鲁格襟翼凹腔所产生的离散噪声特征频率略高。如图26所示,通过对比开缝前缘克鲁格襟翼和无缝克鲁格襟翼远场噪声特性,发现对于无缝克鲁格襟翼,中、低频离散噪声消失,但是主翼上的克鲁格襟翼折叠腔内同样会有自激振荡现象发生,在低频出现了多重离散噪声。如图27所示,利用带通滤波的方法分析低频离散噪声的时频特性,发现低频多重离散噪声具有模态切换特性,这进一步证明了折叠腔内存在着自激振荡现象。

图24 前缘克鲁格襟翼构型凹腔及折叠腔流动示意图[16]

图25 克鲁格襟翼远场噪声特性[16]

图26 开缝、无缝、无凹腔以及无折叠腔的克鲁格襟翼构型远场噪声频谱[16]
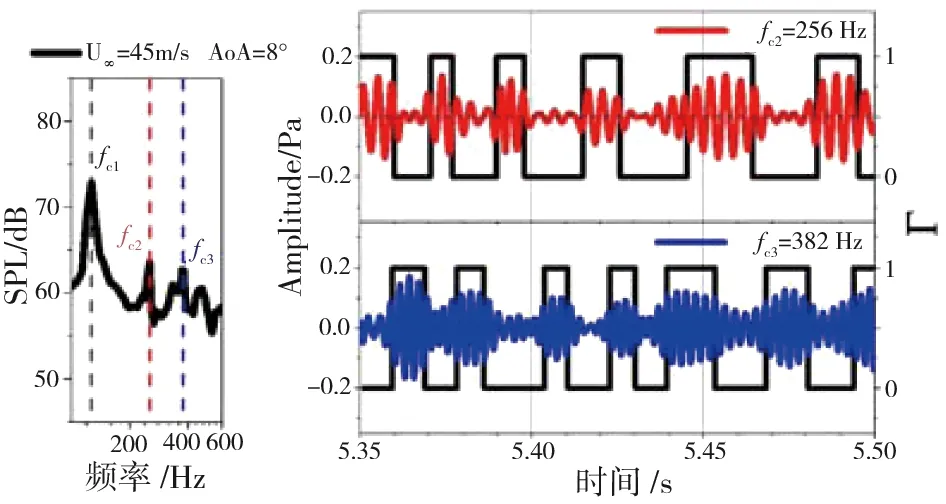
图27 来流速度为45 m/s时滤波分析结果[16]
2.6 前缘下垂远场噪声机理研究
如图28所示,研究了无缝、无腔的前缘增升装置——前缘下垂,在后缘铰链襟翼展开和收起两种状态的低频噪声特性。发现了对于前缘增升装置为前缘下垂,后缘铰链襟翼被收起的状态,远场噪声基本为宽频噪声。来流迎角的改变对低频宽频噪声幅值影响比较明显。此外,随着来流速度的增加,前缘下垂增升构型所产生的宽频噪声幅值随之增加。其中,低频宽频噪声频谱曲线与Ma数的5次方幂次律吻合良好,而中高频宽频噪声频谱曲线与Ma数的6次方幂次律吻合良好。对于前缘增升装置为前缘下垂,后缘铰链襟翼展开的状态,远场噪声依旧是以宽频噪声为主,其远场噪声特性与后缘铰链襟翼收起的情况相似,并且没有新的离散噪声引入。但是,此时的宽频噪声幅值相较于襟翼收起状态较高,一部分是由于模型的有效迎风面积增加,另一部分是由于后缘铰链襟翼附近的流动导致。
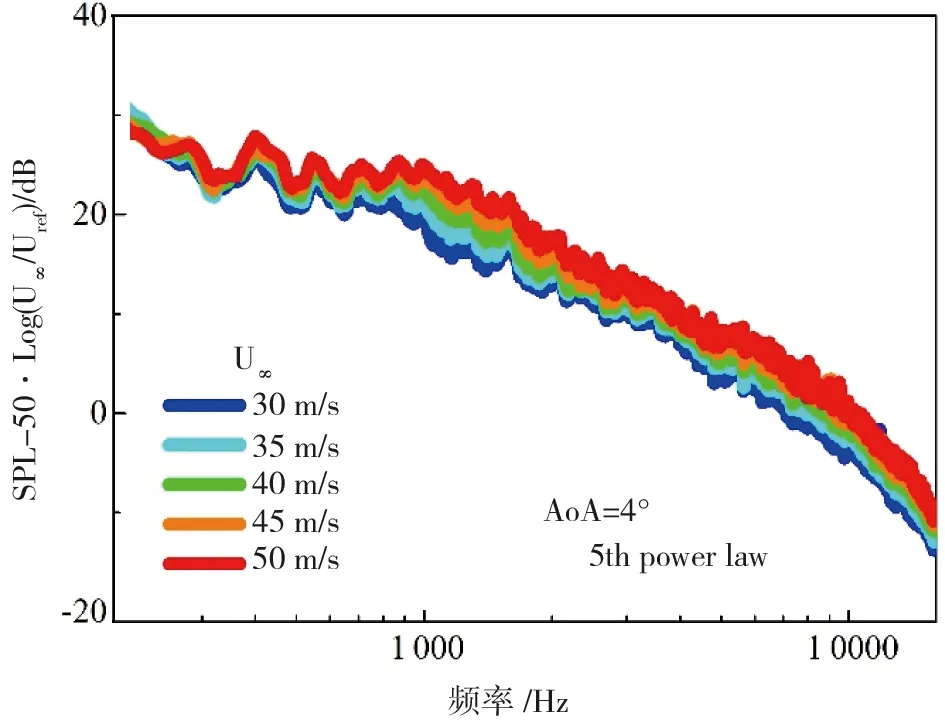
(a) 4°迎角实验结果
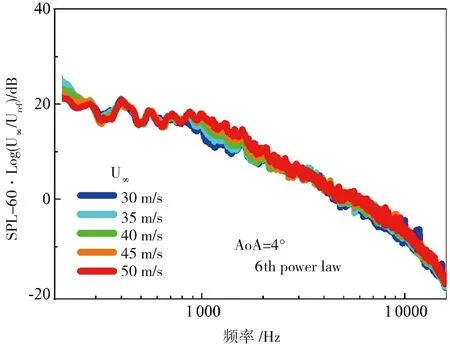
(b) 6°迎角实验结果 图28 前缘下垂、后缘铰链襟翼远场噪声特性[16]
3 起落架气动噪声特性实验研究
陆士嘉实验室围绕飞机起落架及其主要发声部件如空腔、柱体等开展了详细的气动声学试验研究,进一步揭示了这些部件的主要噪声特性。还开展了相关的降噪技术研究,对降噪效果和降噪机理进行了讨论。
3.1 LAGOON起落架标模实验研究
二轮起落架是最简单的一种起落架构型,因而被广泛研究。GUO Yueping等人在波音的低速气动声学风洞(LSAF)中对全尺寸波音737起落架进行了气动噪声实验。通过将起落架分解为不同部件的组合并分别进行声学测量,GUO Yueping等人发现起落架的噪声按照频率大小可以分为低、中、高三部分。其中,低频噪声来自于起落架的轮胎,中频噪声来源于起落架主支柱,而高频噪声来源于孔、线等细小部件,且每一部分的噪声与速度的缩比准则不相同。Ura等人在JAXA风洞中测量了不同轮胎组合形式的两轮起落架噪声,证实这种类型的起落架低频部分噪声主要来自于支柱、连接杆等部件而高频部分噪声主要来自于两轮内侧的区域,此外,两个轮胎的间距对起落架中频部分的噪声大小有明显的影响,大的轮间距构型的噪声要明显低于小的轮间距构型的情况。Yokokawa等人在日本JAXA风洞和RTRI风洞中对某复杂二轮起落架模型分别进行了声源定位测量和远场早测量,并详细分析了各个起落架部件对总噪声的贡献率,结果表明轮胎和两轮间的连接轴是最主要的噪声源,且细小部件对0.7 kHz~5 kHz频域内的噪声贡献也很大。NASA和湾流公司曾对G550飞机的前起落架在实际安装情况下的近/远场噪声进行过测量,发现完整构型的低、中、高频噪声源分别位于轮胎、扭矩臂和灯组部件,而移除某些细节部件后将会使高频噪声源从灯组部件移动到扭矩臂和主支撑附近。近期,空客公司和法宇航、德宇航等机构共同合作完成了LAGOON项目,该项目测量了A320飞机1∶2.5缩比的简化前起落架模型的流场和声场数据,并成为机体气动噪声问题数值模拟的一个标模。McCarthy等人注意到两轮起落架会在1.5 kHz附近产生一个纯音噪声,通过在两轮之间添加分隔板发现该纯音噪声被很好地抑制住,证实了该纯音噪声是由两轮内侧空腔之间的声共振现象产生的。Casalino等人对该起落架侧边噪声中出现的三个纯音噪声产生机理进行了详细地分析,并揭示了这些纯音的产生机理其实是由轮胎内侧一组正对空腔的声共振现象,而每个纯音对应的激发模态也各不相同。
本文通过风洞试验对简化A320前起落架的LAGOON标模远场噪声辐射规律建立了相似关系。试验结果发现起落架内侧空腔产生的噪声要明显大于其他部件涡脱落现象产生的噪声,因此远场噪声频率采用He相似准则比St相似准则更适合;此外,通过分析远场噪声的马赫数比例律关系,进一步揭示该起落架噪声强度随速度的变化有两类不同的变化规律:对紧致声源满足速度6次幂关系而非紧致声源满足7次幂关系。如图29所示,该噪声归一化规律通过将D5风洞试验结果与LAGOON项目结果对比得到了验证,并可以用于风洞试验结果外推并预测真实飞行的噪声大小。
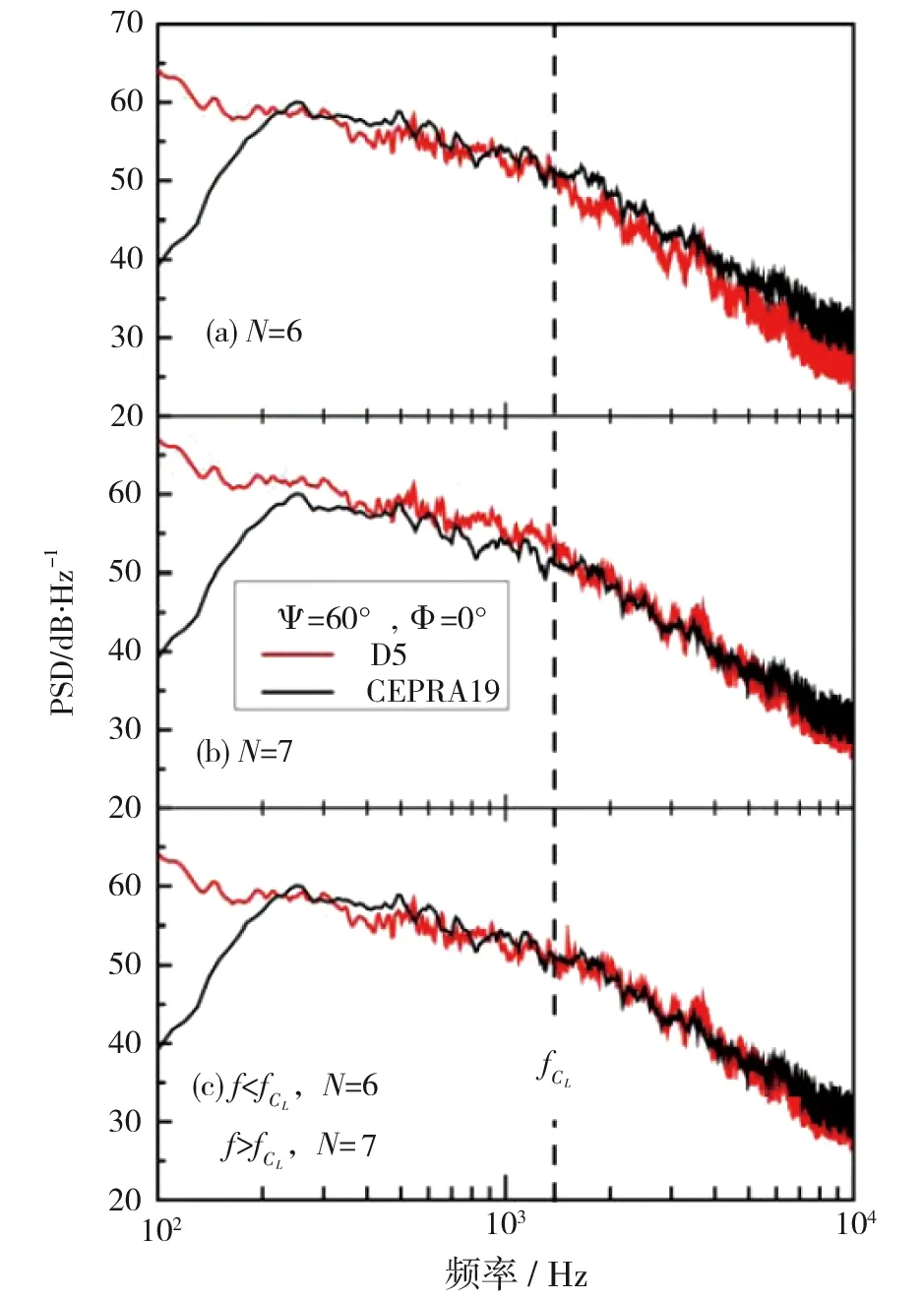
图29 D5测量结果与LAGOON项目结果对比[46]
如图30所示,通过试验研究发现前起落架向远场辐射的高频离散噪声与来流速度无关,因此是由轮胎内侧环形空腔的声共振现象激发。定量分析发现起落架侧边三个离散噪声有着不同的声共振反馈回路、声模态和具体的激发区域。

图30 起落架侧边离散噪声频谱特性[46]
尽管已经确认纯音噪声产生机理是起落架内侧空腔声共振原理,但是LAGOON模型的轮胎内侧空腔的深度直径比(=)仅为0.23,是一个明显的浅腔,不应该产生很强的声共振激发的纯音,这与过去声共振现象通常出现在>4的深腔中的经验不一致。
设计一个排除法实验,使用多种空腔局部遮挡的方法来破坏某些特征尺度的声共振现象,通过比较纯音的抑制规律来进一步确定纯音噪声对应的特征尺度和模态数。实验一共测试了四种局部遮挡方法,一是两侧空腔全部用铝制平板遮挡的方法(两侧遮挡方法),二是两侧空腔的前半部分用铝制平板遮挡的方法(前侧遮挡方法),三是两侧空腔的后半部分用铝制平板遮挡的方法(后侧遮挡方法),四是仅有一侧的空腔全部被铝制平板遮挡的方法(单侧遮挡方法)。这四种遮挡方法的内侧剖面示意图如图31所示。

图31 起落架轮胎空腔四种遮挡构型示意图,其中红色实线代表用于遮挡的铝制平板[53]
通过比较可以发现前侧遮挡能够完全抑制前两个纯音的产生,总体效果与两侧遮挡的情况非常接近,如图32所示;相反地,后侧遮挡则仅能非常有限地降低纯音的强度,在某些角度下甚至增大了纯音的强度。这就说明前两个纯音仅产生于轮胎内侧空腔的前半部分,而受后半侧环形空腔的影响则比较小。这主要是因为气流流过后半侧空腔时,受中间支撑轴圆柱的影响,沿空腔深度方向的流体脉动及声压脉动都会变弱,使得深度方向的空腔声共振很难形成。
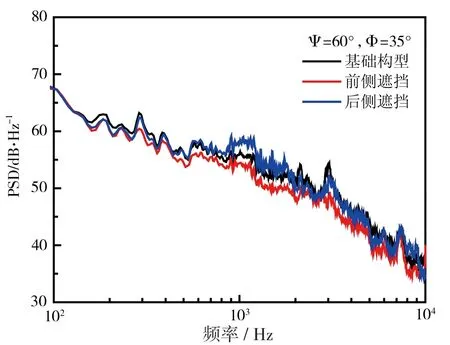
图32 起落架空腔前侧遮挡和后侧遮挡对侧边噪声的影响[53]
此外,如图33所示,利用小波分析对更简化的环形空腔近场噪声测量结果表明存在三种不同的离散噪声产生机理,有的是单独激发,各个离散峰之间没有任何联系,对某个离散峰进行降噪控制不会影响其他离散峰的情况;有的几个峰是交替激发的,一个峰被激发,另一个峰则不会激发;还有一类峰是主要声能量集中在一个主频下,其他离散峰通过主能量峰的振幅调制现象产生的。
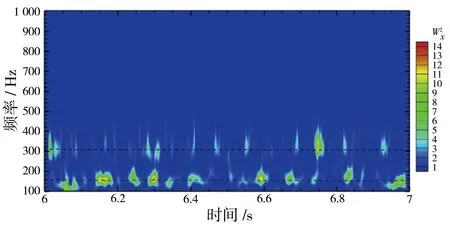
图33 腔声小波分析结果[45]
3.2 空腔气动噪声机理及降噪研究
陆士嘉实验室围绕大型客机起落架系统中的腔体部件噪声进行了基础性的研究。先是研究了带起落架轮毂空腔的圆柱形与环形空腔内的声共振噪声,然后研究了代表起落架舱的方腔噪声,以及应用于方腔流动上的简易被动降噪措施的功效。
空腔流动所引起的噪声问题涉及到流体力学中非定常分离流、涡动力学、自由剪切层的不稳定性、湍流剪切层中拟序结构、声与流动的相互作用等基本前沿问题。对于刚性壁面的空腔,空腔噪声根据其产生机制可分为两类:声共振和自激振荡。
声共振是由空腔内部的驻波产生的,其频率一般相对较高,对应的波长与空腔的尺寸在一个量级上或者更小。腔口剪切层内的湍流扰动作为一个随机噪声源的存在,所产生的噪声本来是宽频的。但在空腔这个半封闭空间中,只有接近空腔固有频率的噪声才能在驻波的作用下被最大程度地加强,这便形成了声共振噪声。这样的驻波会根据空腔的尺寸在深度方向、流向、展向(圆腔就是在径向)上形成。
自激振荡离散噪声是由流体动力学行为和声学行为相互强耦合作用产生的,二者之间存在着复杂的相互作用。从能量的角度看,一方面是从涡模型向声模型转化,涡的存在导致声学行为的产生;另一方面是从声模型向涡模型转化,声学行为刺激诱导涡的产生,两者相辅相成,缺一不可。
本文从声共振特性出发,以环腔为例结合气动声学风洞试验与理论公式推导,建立了基于单点气动噪声频谱测量的预测空腔中不同模态声共振噪声谱密度空间分布的分析模型。该模型能在波动方程解析解的基础上借助风洞试验测试某一关键点的近场噪声频谱数据进而推测出腔内空间的声共振强度分布,如图34所示。在该模型中,声共振模态是由正奇数阶的深度模态与非负整数阶的径向模态和周向模态组合而成,并且阶数越低的模态谱密度越高。声共振的频率不受来流马赫数影响而只依赖于空腔尺寸大小,其预测公式中的深度需要经过与腔口特征尺寸和该模态所处的频率相关的公式修正为有效深度。

图34 圆腔内声共振模态分析[50]
如图35所示,在对声共振行为进行时频分析时发现,声共振具有湍流间歇性的特征,各模态之间不存在调制现象,其不同模态的小波系数幅值归一化后在时间上的概率分布函数具有很好的相似性,且近似服从自由度为7的卡方分布。大体上,“模态共存”与“模态切换”行为出现的概率是均等的,且各行为持续的时间非常短并会快速互相转换。在只改变深度模态的两组噪声之间“模态共存”行为占据微弱优势。

图35 声共振附近频率噪声小波系数云图[54]
从涡模态的角度出发,本文也研究了方腔中自激振荡涡声耦合机理。自激振荡现象本质上来源于腔口剪切层内小尺度旋涡的融合增长并以行波的形式滚动最后与后壁面撞击,不同模态的旋涡运动产生了对应模态的自激振荡离散声,如图36中烟线实验结果所示。在越深的腔中,因与1阶深度模态的耦合作用更强因而自激振荡离散峰越尖锐。从远场噪声的指向性问题来看,自激振荡声最主要的传播方向为过顶平面的上游方向。增加空腔来流边界层的厚度对剪切层厚度的影响不是很明显,但会显著提高剪切层的高度,使其内部能量最强的地方与后壁面的碰撞被削弱,进而削弱了自激振荡噪声。空腔长度的增加则会降低剪切层平均高度并显著增加其厚度,这会让能量更加分散而无法形成集中的尖频噪声,如图37所示。

图36 方腔烟线实验瞬时照片[54]

图37 不同来流边界层下腔体内自激振荡远场噪声谱[54]
如图38所示,在降噪研究方面,分别为在空腔前缘布置不同尺寸的楔形体和通过填充使得空腔内壁面倾斜。前缘楔形体措施能够通过抬高腔口剪切层高度的方式抑制其与空腔后壁面的碰撞,进而降低腔内噪声及腔内外自激振荡声。楔形体夹角的大小对降噪效果影响较小,高度越高的楔形体对腔内噪声的抑制作用越大。当较高的楔形体安装到较短的空腔前缘时会将空腔流动转化为后台阶流动。对于远场噪声,越矮的楔形体对噪声的抑制效果越好。

图38 空腔噪声不同降噪措施[54]
方腔前后壁面向内倾斜会有效抑制腔内声共振噪声,但对自激振荡噪声的影响却需要视情况而定。后壁面会抑制自激振荡,而前壁面则会在某些马赫数下增强自激振荡。如图39所示,前者降噪的原因在于倾斜的后壁面能将剪切层碰撞后产生的扰动反射回剪切层中,进而使得展向一致性被破坏,大涡结构提前破碎为小涡,最后让小涡进入腔底部之前就被耗散掉了,因此抑制了声反馈效应进而达到降噪目的。后者增噪原因在于倾斜的前壁面加速了剪切层中的流动,这为其中的扰动涡注入了更多能量,因而增强了这些涡与后壁面碰撞的强度并增益了自激振荡的作用。

(a) 基本构型 (b) 后壁面倾斜构型 (c) 前壁面倾斜图39 三种构型的Q准则瞬时等值面云图,颜色表示马赫数大小[54]
3.3 柱体气动噪声机理及降噪研究
陆士嘉实验室围绕钝体部件气动噪声,主要开展以多种不同尺寸比例工况下圆柱、方柱等典型钝体部件噪声机理以及以圆柱表面螺旋状缠绕细铁丝和包裹吸声材料为主的降噪技术研究。
对起落架噪声频谱分析发现圆柱形部件如主支柱等产生的涡脱落噪声会对起落架噪声有很大的贡献,因此以圆柱简化模型进行了研究。在飞机机体噪声这一工程领域圆柱部件的雷诺数都比较高,其流态范围通常处于高亚临界状态或临界状态,因此对高雷诺数圆柱的气动噪声问题的研究就显得很重要。20世纪70年代以来对圆柱的气动噪声特性的研究有过一些实验和计算方面的进展,如Revell等人曾对雷诺数在45 000~450 000和马赫数在0.1~0.5范围内的表面光滑及粗糙圆柱的气动噪声进行了大量的实验研究,获得了丰富的实验结果,其实验测量结果一直被作为CFD计算的参考数据。此外他们还发现圆柱远场噪声的声压级很大程度上受到阻力系数的影响。King等人通过实验研究比较了不同截面圆柱的远场噪声特性,Iglesias等人则进一步研究了圆柱在不同倾角下的噪声特性。Fujita填补了高亚临界和超临界雷诺数范围内圆柱噪声在实验领域的空白,并检验了端板效应的影响,他发现当圆柱绕流的流态从亚临界流态变到超临界流态时,随着阻力的突然下降,远场噪声也会迅速降低。Cox等人运用可压缩N-S方程求解100 除圆柱噪声特性研究外,最重要的还是圆柱的降噪研究。二维圆柱的气动噪声主要产生于非定常涡脱落现象导致的圆柱表面强烈的压力脉动,通过一定的手段削弱或完全消除圆柱的非定常涡脱落过程就可以实现圆柱降噪的目地。过去对圆柱绕流控制的研究主要集中在流动控制、减阻、降低升力脉动或降低涡激振动(Vortex Induced Vibration,简称VIV)等方面,其中部分有效的流动控制方法及其主要控制机理在综述文献中有总结。这些工作尽管与圆柱降噪控制并不是完全等价,但是具有一定的参考价值。过去曾提出并验证了效果的圆柱降噪控制方法主要包括以下几类:等离子体激励、开槽圆柱、波状圆柱、多孔介质材料遮挡、绒毛材料遮挡、扰流板或分隔板和螺旋缠绕铁丝等。 图40 无量纲声压级频谱[28] 陆士嘉实验室开展了亚临界雷诺数下的圆柱绕流气动噪声研究。实验段的风速范围在30 m/s~80 m/s,雷诺数为0.41×10~1.1×10。此时,附面层仍为层流分离,而尾迹已转变为湍流涡街。如图40所示,圆柱绕流远场噪声声压级的尖峰值对应的涡脱落无量纲频率St在一个很小的范围内波动,与Revell的实验和Norberg的经验公式得到的St基本上相差不大,声压级近似与U成正比,表明圆柱绕流气动噪声为典型的偶极子声源。 如图41所示,以串列双圆柱模型为基础模型研究了起落架部件间相互干扰产生的噪声特性。试验结果表明双圆柱噪声与间距密切相关,小间距时噪声低而大间距时噪声大。将螺旋缠绕铁丝技术应用到双圆柱降噪中,发现对上游圆柱进行降噪控制能够有效地消除上游圆柱分离的剪切层或脱落涡与下游圆柱壁面的非定常相互作用,是实现双圆柱降噪的关键,此外,在大间距时该降噪方法的降噪效果要明显优于小间距时的降噪效果。进一步比较三种不同排列方式的双圆柱噪声结果发现,将小圆柱放置在大圆柱上游是一种最低噪声的排列方式,可以为起落架部件低噪声布局提供一定的参考。最后,通过小波分析发现在小间距时双圆柱产生的离散噪声具有模态切换的时间特性,其物理本质是双圆柱流动的非稳定特性。 图41 等直径串列双圆柱远场声压信号的时间序列 在实际的工业应用中,有限长的三维柱体更为常见,因为大部分的柱体结构并不能满足二维柱体无限长或者两端加端板的条件,如汽车天线及后视镜等。如图42所示,不同于二维方柱,三维方柱尾迹区的流场会受到边界处流动的影响,且在不同的长径比下,尾迹区会产生更为复杂的流动现象,如分区流动等。与之相对应的,在不同长径比下,三维柱体的远场噪声也会表现出不同的特性。如图43所示,随着方柱长径比的增加,由于流动分区现象的产生,远场噪声中的离散声个数会从0增加至3。与之相对应的,可以将方柱的长径比划分为R0、RI、RII与RIII四个区间,在RI、RII以及RIII区间内,远场噪声中的离散声的类型分别为P1、P1&P2以及P1&P2&P3,其中P1、P2与P3离散声分别主要对应的是顶部下洗流动结构,中部的展向涡结构以及底部的上洗流动结构,如图42所示。对于14 mm直径的方柱,其4个区间分别对应的长径比的范围为: 图42 壁面上有限长方柱流场[35] 图43 壁面上有限长方柱气动噪声特性[35] R0(L/D<2),RI(2≤L/D<10),RII(10≤L/D<14),RIII (L/D≥14);而对于30 mm直径的方柱,其4个区间分别为:R0(L/D<2),RI(2≤L/D<9),RII(9≤L/D<17),RIII(L/D≥17),如图44所示。在不同的区间内,方柱的气动噪声均满足偶极子特性,且通过计算结果可知,三维方柱的远场噪声中离散声主要受到横向脉动的影响,而流向脉动力主要影响的是离散声频率倍频处的噪声强度。 图44 近场噪声离散声St数随长径比的变化规律[35] 降噪技术研究主要以圆柱为主的起落架支柱模型作为钝体噪声降噪技术研究对象。对在圆柱表面螺旋状缠绕细铁丝的声学与流场进行了测量。首先通过参数化研究分析了该方法降噪效果受铁丝螺距和铁丝密度的影响规律,发现大螺距和大铁丝密度有更好的降噪效果,最优的降噪构型能降低圆柱远场噪声达17 dB,如图45所示。 图45 单圆柱绕细铁丝远场噪声特性[25] (a) 光滑圆柱 (b) 加控圆柱图46 光滑圆柱和加控圆柱尾迹区雷诺应力对比 如图46所示,通过对加控前后圆柱尾迹区流场特性的测量分析,发现光滑圆柱的时均流线关于尾迹中心线几乎是对称的,脱落的旋涡也非常靠近圆柱表面;但是对于加控后的圆柱,其时均流线却存在明显的不对称性,流线、脱落涡的位置等都大不相同,这就说明加控圆柱的尾迹中存在非常明显的三维流动。造成这一现象的主要原因是加控圆柱截面形状沿展向分布不均匀,从而使得气流在圆柱两侧的分离点位置并不对称且分离线沿展向发生弯曲。进一步比较脱落涡相对于圆柱表面的位置,发现不论在哪个截面,加控圆柱尾迹中的脱落涡总是在更下游的位置形成,可以定性地表明加控后脱落涡与圆柱表面相互作用的强度降低,使圆柱表面的压力脉动降低。 如图47所示,对覆盖软性多孔材料的起落架支柱模型进行了声学测量。试验使用了聚氨酯海绵、绒毛织物、喷胶棉、海藻绵四种软性多孔材料覆盖在支柱外表面,采用自由场传声器获取远场声谱特性,如图48所示。 图47 覆盖绒毛织物支柱远场噪声测试 图48 采用不同包裹材料圆柱绕流噪声特性[40] 声谱结果显示覆盖聚氨酯海绵和绒毛织物能使涡旋脱落引起的单音区域变得更窄,峰值更低但没有被完全抑制。覆盖喷胶棉和海藻绵,能使支柱单音完全消失,但海藻绵会引起高频噪声增加。最优秀的降噪材料喷胶棉,能完全抑制单音噪声和完全消除宽带噪声。覆盖多孔材料后,尾迹的大尺度涡脱落结构得到有效抑制,多孔材料减弱了近尾迹场的速度功率谱密度峰值,减小了尾迹区的速度,拓宽了尾迹的宽度,增大了涡形成长度;软性多孔材料使得支柱尾迹区两侧剪切层变得细长,削弱了剪切层之间的相互作用,同时减小了尾迹区的速度脉动。 图49 起落架及空腔噪声耦合特性 在起落架舱简化模型与起落架的耦合噪声场中,空腔噪声在低频段占优,而起落架噪声在中频段占优,如图49所示。二者组合在一起后会对中频段的空腔的声共振噪声以及支柱涡脱落噪声产生正向的非线性耦合作用,但不会影响到空腔的自激振荡峰。从空腔对起落架噪声的影响来说,空腔后壁面的阻滞作用会缩短支柱尾迹中的回流区,并增强其湍流脉动,进而增强了支柱表面的压力脉动,这会让支柱辐射到远场的低频噪声增加。从起落架对空腔噪声的影响来说,支柱尾流与空腔后壁面的撞击也会对后壁面中部区域产生较剪切层的撞击更为强烈的压力脉动,同时在支柱的阻滞作用下,撞击后破碎的小涡会在支柱与后壁面之间迅速地耗散掉而非顺着空腔底部流向前缘壁面,这就给支柱与前壁面之间的流场带来更少的扰动从而让其更加稳定,使得流向上的声共振驻波被流动干扰更少而得到增强,如图50所示。 图50 空腔底面压力信号相关系数云图[28] 本文以北京航空航天大学陆士嘉实验室气动声学风洞在近十几年来在气动噪声研究方面的典型结果,通过梳理在不同试验条件和工况下多段翼、起落架、腔体部件和钝体部件的典型气动噪声研究结果和方法,阐明了当下气动声学风洞研究中常见的研究思路和方法,有助于研究者参考学习。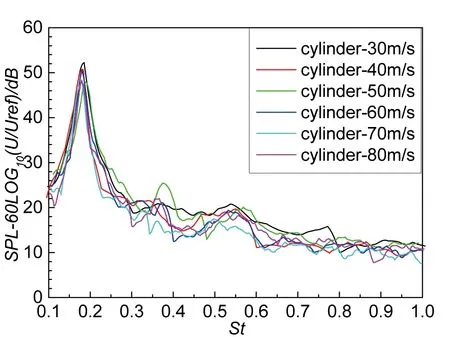









3.4 带舱起落架气动噪声研究


4 结论

