高拱坝参数反演的Jaya-高斯过程回归模型

马建婷，康 飞，姜成磊，向正林，王一帆

(1.大连理工大学水利工程学院，辽宁 大连 116024； 2.吉林省水利水电勘测设计研究院，吉林 长春 130021；3.南方电网调峰调频发电有限公司，广东 广州 510630)

21世纪以来，我国高拱坝建设取得了飞速发展，先后建成了小湾、锦屏一级、溪洛渡等多个特大型工程[1-2]。正确估算坝体混凝土和坝基岩石的材料参数是进行拱坝安全评价与建立大坝安全监控模型的关键[3]。拱坝物理力学参数反演分析是一个多参数组合的大空间搜索问题，求解算法十分重要[4-5]。在拱坝的智能优化反演分析方面，刘耀儒等[6]将改进的并行遗传算法用于溪洛渡拱坝位移反演分析；李火坤等[7]采用粒子群优化算法反演得到二滩拱坝的实际动弹性模量；Kang等[8]提出了一种求解反分析问题的混合单纯形人工蜂群算法；练继建等[9]建立了反映大坝弹性模量与位移之间非线性关系的BP神经网络模型，并将其用于李家峡拱坝材料参数反演；Liu等[10]在反演过程中采用无约束拉格朗日支持向量回归来代替大型有限元计算，以获得弹性模量与变形的关系。

目前的反演分析方法存在两方面不足：①基于有限元模型求解大坝静动力响应往往需要耗费大量的计算时间，对于某些大型结构甚至无法求解；②随着新型群体智能算法的提出，反演分析的精度还有待进一步提高。为此，本文将Jaya智能优化方法以及高斯过程回归(Gaussian process regression，GPR)理论引入大坝安全监控领域，提出了基于Jaya-高斯过程回归代理模型的拱坝物理力学参数反演分析方法。

1 混凝土坝反演分析基本理论

对于大坝工程，建立大坝与坝基位移监控模型以后，依据正分析的结果，通过相应的理论反求大坝和地基的材料物理力学参数，即为大坝位移反演分析[11]。若计算分析方法采用有限元法，则反演分析即为大坝的有限元模型修正。有限元模型修正是指利用静动力测试结果修改有限元模型的刚度、质量、边界条件等参数，修正后的模型不仅能够反映结构的实际状态，还可以用于损伤识别、安全评价等方面。

优化反演分析法是一种直接的反演分析方法，其适用性较强，通过建立目标函数，将反演问题转化为参数最优化问题，通过不断迭代逐次修正试算值，直至获得最佳值[12]。静力计算采用有限元模型，基于位移监测数据分离水压分量反演坝体参数的数学模型可表达为

(1)

式中：K为刚度矩阵；u为位移向量；R为荷载向量；ωi为权重，通常取值为1；Δuie为实测位移的变化值；Δuin为有限元计算得到的位移变化值；m为测点数目。

2 基于Jaya-高斯过程回归代理模型构建

2.1 Jaya算法

Jaya算法是一种新型智能优化算法，由Rao[13]于2016年提出。Jaya算法设计的基本思想是群体应趋向最优解移动而远离最差解。该算法，除了常规的群体规模和搜索终止条件参数，无需输入其他特定参数；同时，更新方程只有一个，算法简单、易实现。

Jaya算法的数学描述如下:令g(z)为待优化的目标函数，在任意迭代次数a中，Zj=(zb1,zb2,…,zbD)(b=1,2,…,N)为第b个候选解(D为设计变量的个数，N为群体规模)，Pb=(pb1,pb2,…,pbD)为第b个候选解寻找的最优解。通过式(2)生成新的候选解，不断更新，逐渐收敛到最优解。

Za+1,b=Pa,b+r1(Za,best-|Pa,b|)-r2(Za,worst-|Pa,b|)

(2)

式中：Za,best、Za,worst为第a次迭代整个群体中的最优解和最差解；r1、r2为在(0,1)内的2个随机数。

2.2 GPR

GPR最早由Rasmussen等[14]提出，是一种机器学习新回归方法。其最大的优点是能够从训练数据中学习平滑参数和噪声以提供不确定性估计[15]。

GPR预测均值和协方差为

(3)

cov(f*)=K(X*,X*)-

(4)

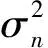
由(3)式可知，协方差函数对GPR预报结果有一定的影响。因此，协方差函数的选择对于GPR建模的成功具有重要意义[15]。常用的协方差函数为

(5)

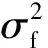
2.3 反演分析步骤

反演分析基本步骤如下：

步骤1生成样本点。确定待反演区域弹性模量的取值范围，采用拉丁超立方抽样生成样本点。

步骤2构建样本集。样本集由样本点及其各监测点的相对位移组成。采用有限元进行数值模拟，计算出各监测点的相对位移。

步骤3建立GPR代理模型。利用前2步得到的训练样本集建立基于GPR的代理模型。

步骤4检查GPR代理模型的准确性。利用步骤1和步骤2得到的测试样本，采用均方根误差(RMSE)作为样本精度的评价指标[16]，检验所建立的GPR代理模型的准确性。如果精度不满足，则返回到步骤1，生成更多的训练样本点，得到更准确的代理模型。

步骤5参数优化反演。利用可代替有限元计算的GPR代理模型以及引入的智能优化算法进行参数优化反演，得到最优解，即为反演分析结果。

3 算例验证

某特高拱坝最大坝高277 m，为混凝土双曲拱坝，有限元模型如图1所示，坝体和基础共分为11 013个单元，51 917个结点。采用有限元正分析的计算结果来模拟大坝位移观测值的水压分量[3]。选取的大坝变形监测点分别为P1、P2和P3。选取一组弹模E=(E1，E2，E3，E4)=(21，20，13，15)GPa，分别为坝体、底部基岩、左岸基岩和右岸基岩的弹性模量。求得上游水位为820 m和790 m的2种工况下P1、P2、P3测点的相对水平位移分别为16.60 mm、3.22 mm、-2.64 mm，相对垂直位移分别为42.79 mm、45.23 mm、24.81 mm。反演时，选取坝体和基岩的弹模范围为5～40 GPa[16]。

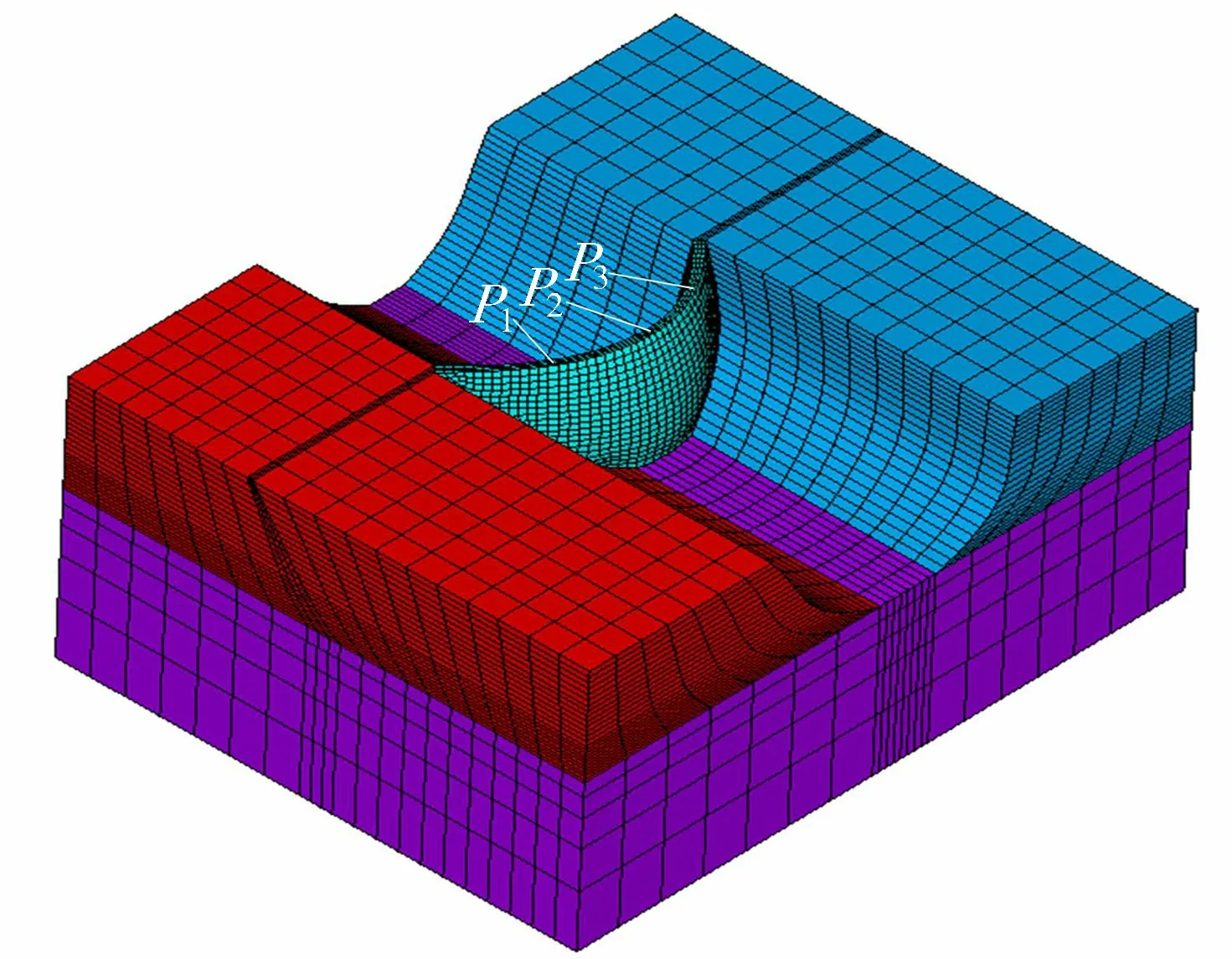
图1 某特高坝体有限元模型

表1 算例3种算法反演结果

为建立Jaya-高斯过程回归代理模型，研究了建模样本数量对精度的影响，将训练样本和测试样本(取为训练样本的25%)的RMSE绘成曲线，如图2所示。根据图2可知，均方根误差呈下降趋势，样本的精度逐渐增加。当样本数量为100D时，均方根误差变化较小。因此，选取样本数量为100D的GPR代理模型代替有限元模型。

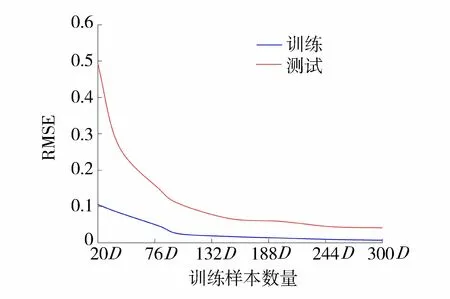
图2 样本均方根误差趋势

在该高拱坝反演分析中引入Jaya算法，并将它与粒子群算法[17](particle swarm optimization，PSO)及灰狼算法[18](grey wolf optimizer，GWO)做比较。3种算法群体规模N=20，最大迭代次数为200，粒子群算法的其他参数参考之前的研究[19]设置。为了避免算法的随机性，将优化算法运行30次[16]。3种算法的反演结果见表1，最优适应值变化曲线和坝体混凝土弹性模量识别过程曲线分别如图3、图4所示。

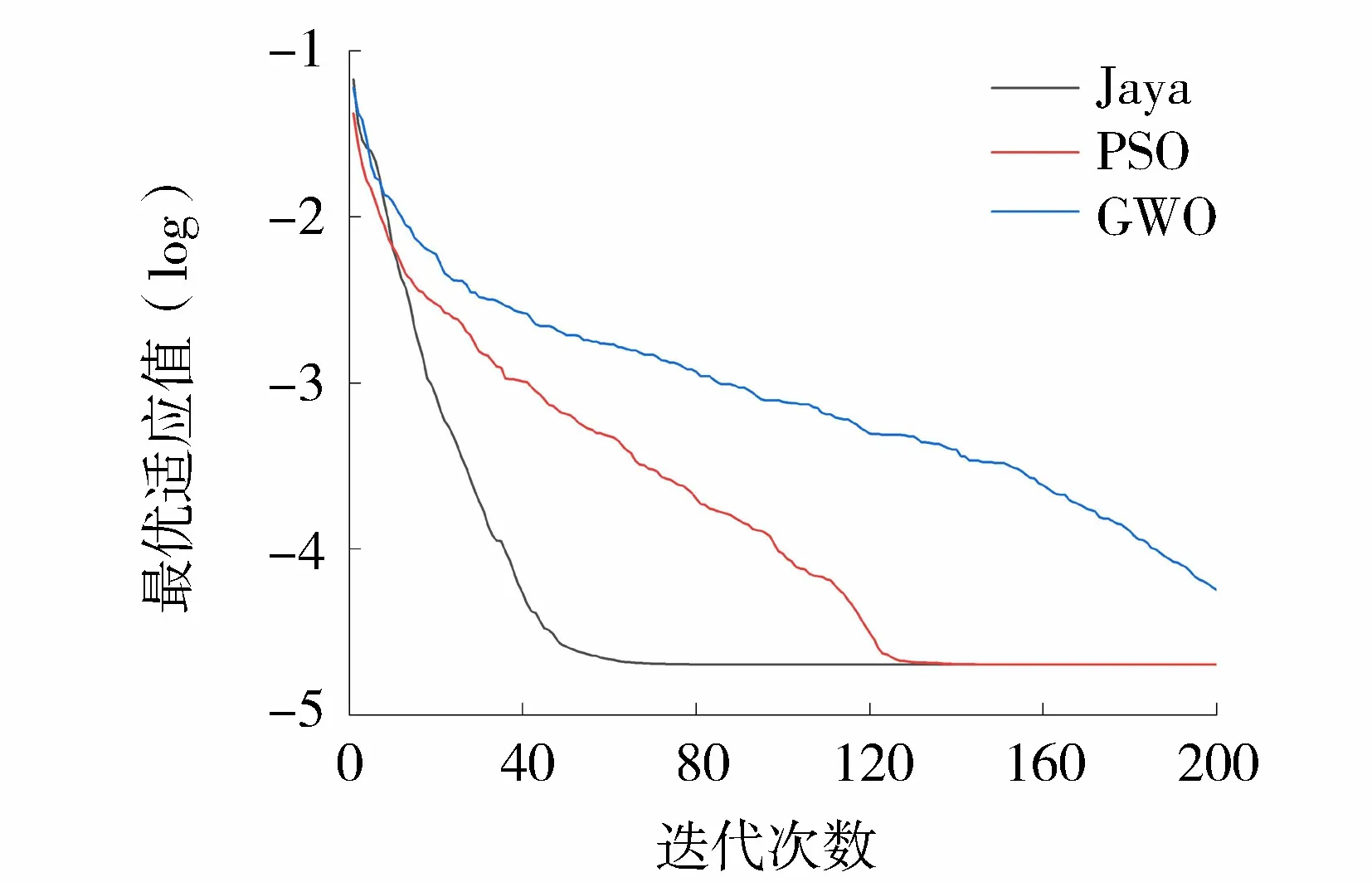
图3 算例拱坝最优适应值变化曲线

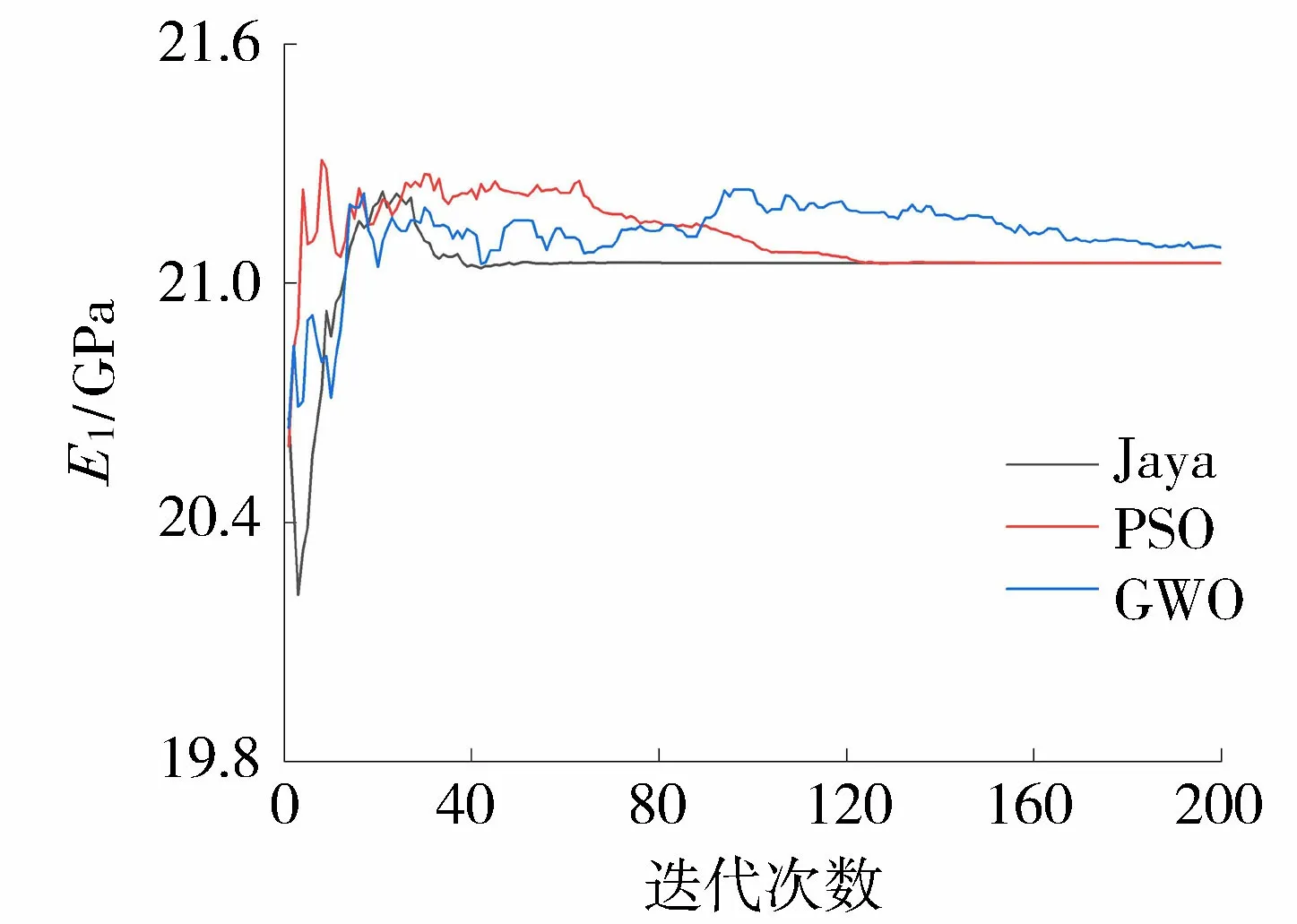
图4 算例拱坝弹性模量E1识别过程曲线

由表1可知，本文提出的反分析策略在该拱坝反演分析中是可行的。且Jaya算法比PSO算法、GWO算法的精度更高。由图3及图4可知，达到收敛时，Jaya算法的迭代次数约为80次，而PSO算法的约为130次，GWO算法却始终没有达到收敛状态。此外，在30次的运行结果中，Jaya算法和PSO算法的反演结果较为稳定，相对误差变化较小；而GWO算法反演结果的相对误差变化较大，最大误差为9.314 6%，最小误差为0.467 1%。

为了研究3种优化算法的抗噪声能力，在监测点的位移分别加3%的噪声，同样运行30次，结果见表2。由表2可知，在加入3%噪声时，Jaya、PSO及GWO算法的反演结果的平均相对误差分别为2.651 0%、2.651 1%和3.285 6%，均较小。因此，在加入3%噪声时3种算法对该混凝土拱坝的反演结果是可靠的。

表2 加入3%噪声3种算法反演结果

在反演用时方面，由表3可知， GPR代理模型比有限元模型节省约87.48%的时间。由此可以看出，基于Jaya-GPR代理模型的拱坝物理力学参数反演分析方法在保持计算精度的同时，计算效率也具有较大的优势。

表3 算例反演用时计算结果

4 实例应用

以西南某高拱坝为例，该高拱坝坝顶高程610.0 m，最大坝高285.5 m，顶拱中心线弧长681.5 m，厚高比为0.216，弧高比为2.451。依据坝体几何参数及设计相关资料，建立有限元分析模型。其中坝基范围为：向上下游、左右岸和河床深部分分别延伸1.5倍坝高，整个模型划分为233 538个单元，261 734个结点，有限元网格如图5、图6所示。边界条件定义为：坝基底部为三向固定约束，4个侧面为法向固定约束。其中坝体混凝土和坝基的材料参数除待反演的弹性模量，其余值均采取设计值。

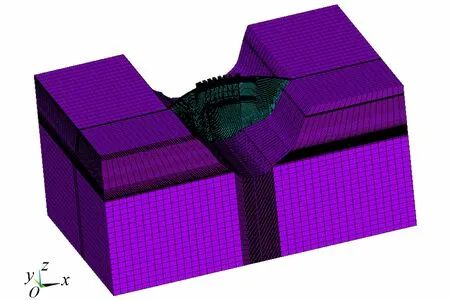
图5 拱坝整体有限元模型

图6 坝体有限元模型

于拱坝左岸坝肩、5号坝段、10号坝段、15号坝段、22号坝段、27号坝段、右坝肩拱布置7组29个正垂线测点用以监测坝体水平位移(图7)。根据监测数据显示7组测线中位于坝体中心线的15号坝段垂线监测到的坝体水平位移最大，且由于切向位移较小，实际观测值的误差相对较大，因此本文将以15号坝段径向位移监测数据作为研究对象开展分析。

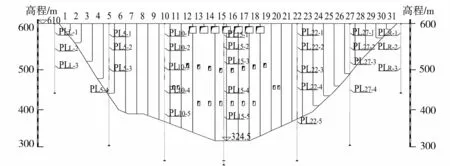
图7 拱坝正垂线及变形测点布置

对于15号坝段的温度监测数据，取与它相邻的16号坝段布置在坝体表面的32个温度传感器和布置在坝体内部的19个应力应变传感器，温度传感器分布图如图8所示，从图8可见拱坝温度测点较多，在应用回归模型时难以考虑全部温度测点，经过分析削减以后，仍有15个，故考虑提取主成分的方式，采用SPSS软件，对15个已有的温度因子进行降维处理，提取前4个主要成分(保留温度测量信息的90.599%)。按照传统多元回归模型的因子选择方法，最终自变量因子设计为

V=(h,h2,h3,h4,TPC1,TPC2,TPC3,TPC4,

-exp(-0.5t))

(6)

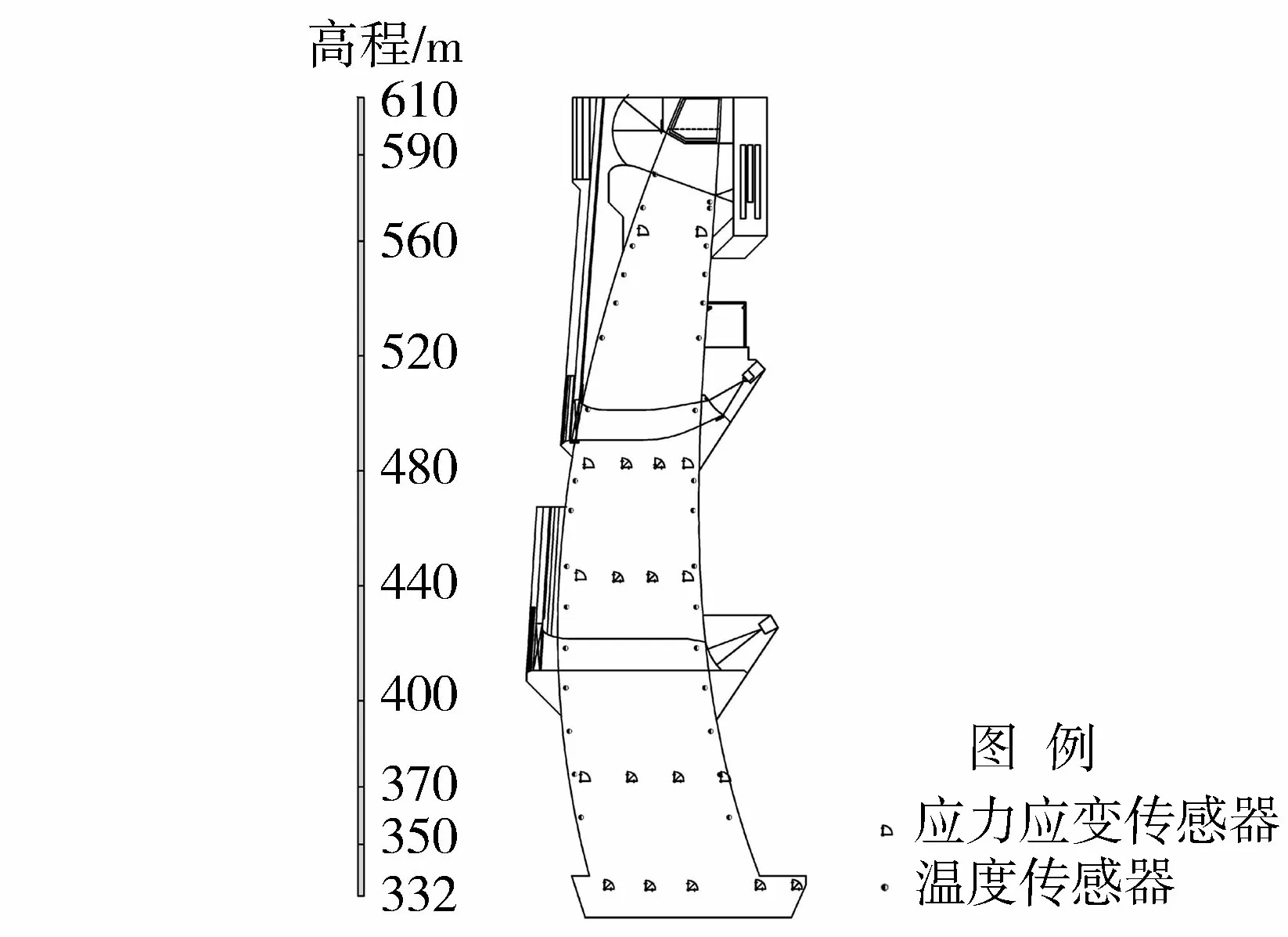
图8 拱坝温度传感器分布

式中：h为水压因子，取上游水深；TPC为主成分分析得到的温度因子；t为时间，取从监测日到始测日的天数除以365。选取测点PL15-1及测点PL15-2在2014年7月6日至2017年11月29日的实测径向位移建立统计回归模型。其中实测值、拟合值及各位移分量结果如图9所示。为计算简便，荷载工况选取上游水位为599.76 m和559.44 m情况下的水压差值作为位移反分析的荷载条件，其计算结果是在水压荷载作用下拱坝的位移差值。

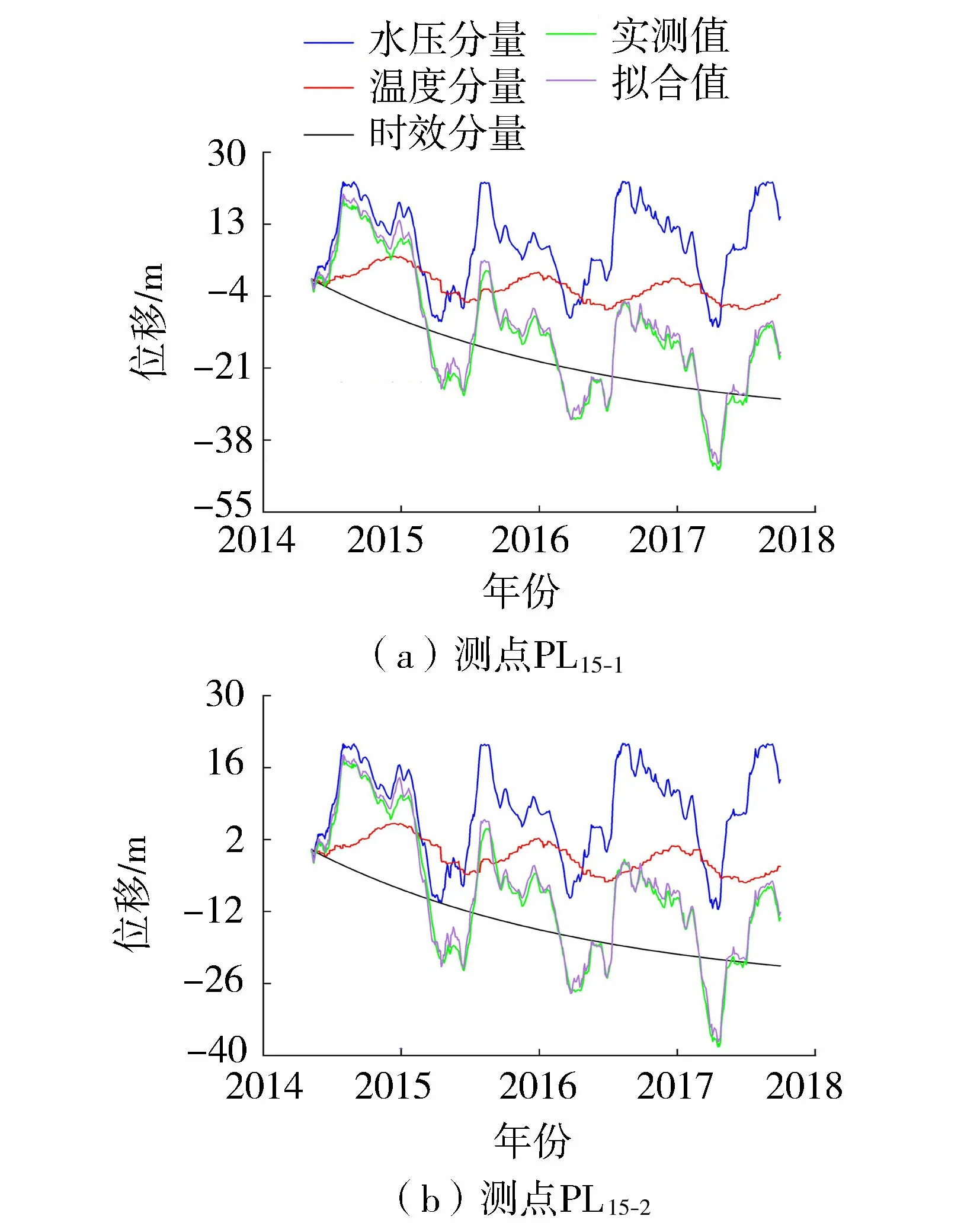
图9 拱坝PL15-1测点各位移分量分离结果

径向位移对应拱坝的极坐标系，需将其进行坐标转换，得到有限元模型坐标系下的位移值，即Δu15-1x= -25.371 8 mm，Δu15-2x= -23.047 2 mm。

根据相关试验资料，混凝土和岩体弹性模量的取值范围设置为：坝体E1=35～60 GPa，地基E2=15～40 GPa。训练样本数量为100D，建立GPR代理模型。3种算法群体规模N=20，最大迭代次数为200，每种算法随机运行30次[16]。3种算法弹性模量的反演结果见表4，最优适应值变化曲线及弹性模量识别过程曲线分别如图10和图11所示。

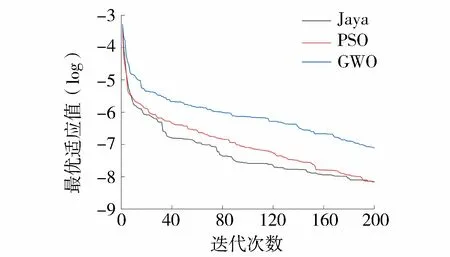
图10 实例拱坝最优适应值变化曲线

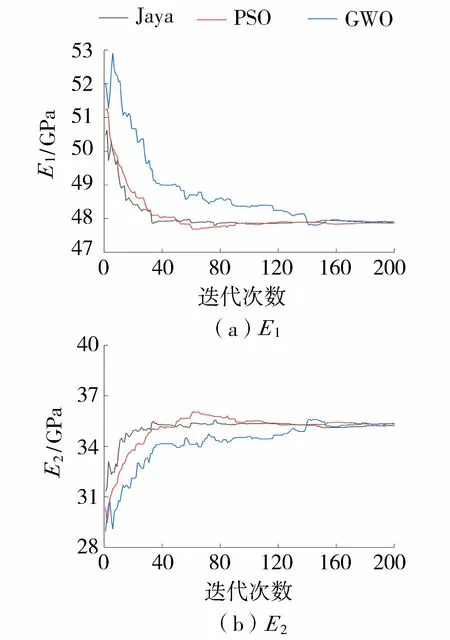
图11 实例拱坝弹性模量识别过程曲线

为了进一步验证反演结果，将上述反演结果，用有限元计算坝体测点在上游水位为599.76 m和559.44 m状态下的位移差值，并与实测位移水压分量差值进行比较。从表4中看出，两者接近，总体误差较小，说明反演的成果是合理的。

表4 实例3种算法反演结果

在反演用时方面，由表5可知，采用GPR代理模型相比有限元模型节省时间约93.75%。进一步证明了所提出的基于Jaya-GPR代理模型能大幅度提高体系反演分析的效率。

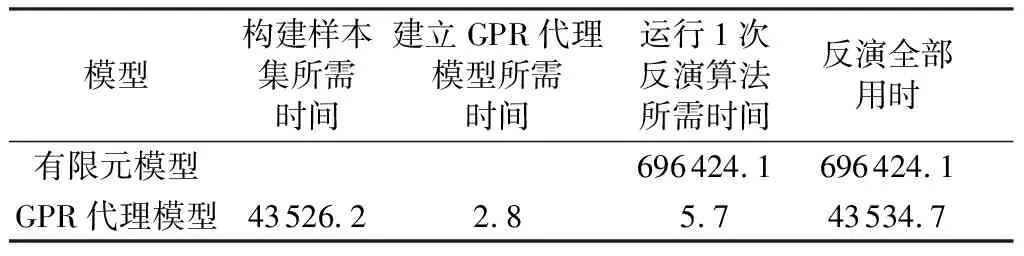
表5 实例反演用时计算结果 单位:s

5 结 论

a.高斯过程回归用于混凝土拱坝反演分析的代理模型是有效的，与有限元模型计算结果一致。

b.与其他算法相比，Jaya算法具有控制参数少、反演精度高、收敛速度快、稳定性好等优点。

c.提出的基于Jaya-GPR代理模型的拱坝物理力学参数反演分析方法能够大幅度的提高反演分析的效率，相比于基于传统有限元的反演方法，用时节省了80%以上。