液滴撞击恒温多孔介质表面的数值模拟
刘毅诚, 李培超
(上海工程技术大学 机械与汽车工程学院, 上海 201620)
液滴撞击动力学问题在生产生活中应用广泛,如金属切削加工时需要进行喷雾射流冷却[1]、打印机喷墨打印[2]和内燃机燃料碰壁燃烧[3]等。多孔介质在生活中无处不在,我们对液滴在多孔材料表面铺展润湿[4]、渗流[5]和吸附[6]等行为的研究也广为关注。
Van Gaalen等[7]对液滴在多孔介质表面渗透吸收进行了数值研究,基于Darcy定律用表面润滑理论和毛细现象解释了多孔基底的吸液行为,并总结了钉扎与移动接触线对渗透速率以及渗透深度的影响。Li等[8]对非连续湿润梯度表面液滴的自运输现象进行了数值分析,通过观察液滴在光滑和粗糙表面上毛管数和质心的变化,发现粗糙带对液滴铺展有显著的阻碍作用。Yuan等[9]在研究表面纹理对湿润性的影响时,提出了一种二级分层结构可以显著提高表面材料的疏水性,并通过数值模拟的方法分析了液滴韦伯数、撞击位置对液滴渗透、湿润的影响。Neyval C等[10]通过数值模拟的方法,研究了雷诺数、达西数及韦伯数等7种无量纲数对液滴冲击多孔介质表面铺展与渗透行为的影响。张新铭等[11]通过数值模拟的方法对石墨泡沫的流动阻力进行了研究,提出了一种基于Ergun渗流方程的泡沫多孔材料模型,可以用来很好的描述石墨泡沫材料对渗流流体的压降作用。
在研究液滴撞击动力学问题时,上述研究者多从液滴润滑理论和多孔材料渗透机理进行研究,考察液滴撞击动力学问题。笔者将在前人研究的基础上,考虑流动与传热之间的相互影响,从多孔介质表面温度、湿润性能和渗透性能等多个角度进行数值模拟,观察各参数对液滴撞击变形的影响,旨在能更好得了解液滴在多孔介质表的铺展与渗透机理。
1 数学模型
1.1 研究方法
笔者运用CFD软件FLUENT对液滴撞击多孔介质问题进行数值模拟实验。液滴撞击变形的过程中涉及到气液两相流相界面的捕捉问题,撞击后动力学过程又涉及到液体在多孔材料中渗透流动的问题以及内部热能传递的问题。在求解液滴渗流问题时,多孔介质宏观概化模型将很好的描述多孔材料对流体的黏性阻力和惯性阻力的作用;局部热平衡假设[12]可以用“有效热性能”来简化描述整个多孔区域(包括流体与固体)内的平均温度。
图1所示为液滴撞击多孔材料的物理模型,假设液滴在下落的过程中形态不变仍保持为球形,初始半径r0=1 mm,在重力加速度g的作用下以一定的速度与多孔介质平板发生碰撞,撞击速度V0=1 m/s。液滴碰壁模型是以坐标轴x轴为旋转对称中心,其正半轴为流体区域,负半轴为多孔区域。
1.2 控制方程
液滴在多孔材料表面铺展与内部渗透沿用了2套不同的控制方程,内部的流体除了受到压差力、重力和黏性剪切力外,还受多孔材料带来的黏性阻力与惯性阻力的影响,其控制方程如下:
流体区域:

(1)

(2)

(3)
多孔区域:

(4)
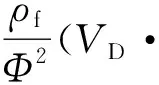
(5)

(6)
根据Ergun方程[14]可知,多孔材料的渗透率K和惯性因子C与孔隙度Φ和平均颗粒直径dp有关:
(7)
(8)
1.3 边界条件
多孔材料的表面是流体区域与多孔区域的交界面,而恒温多孔材料的表面属于传热学第一类热边界条件Dirichlet边界,即:
Tp=T0;
(9)
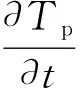
(10)
式中T0为多孔材料的初始温度。
在该边界条件下,多孔材料的表面温度Tp为定值且不随时间t变化而变化。
2 模型验证
2.1 模拟实验验证
模拟结果如图2和图3所示。
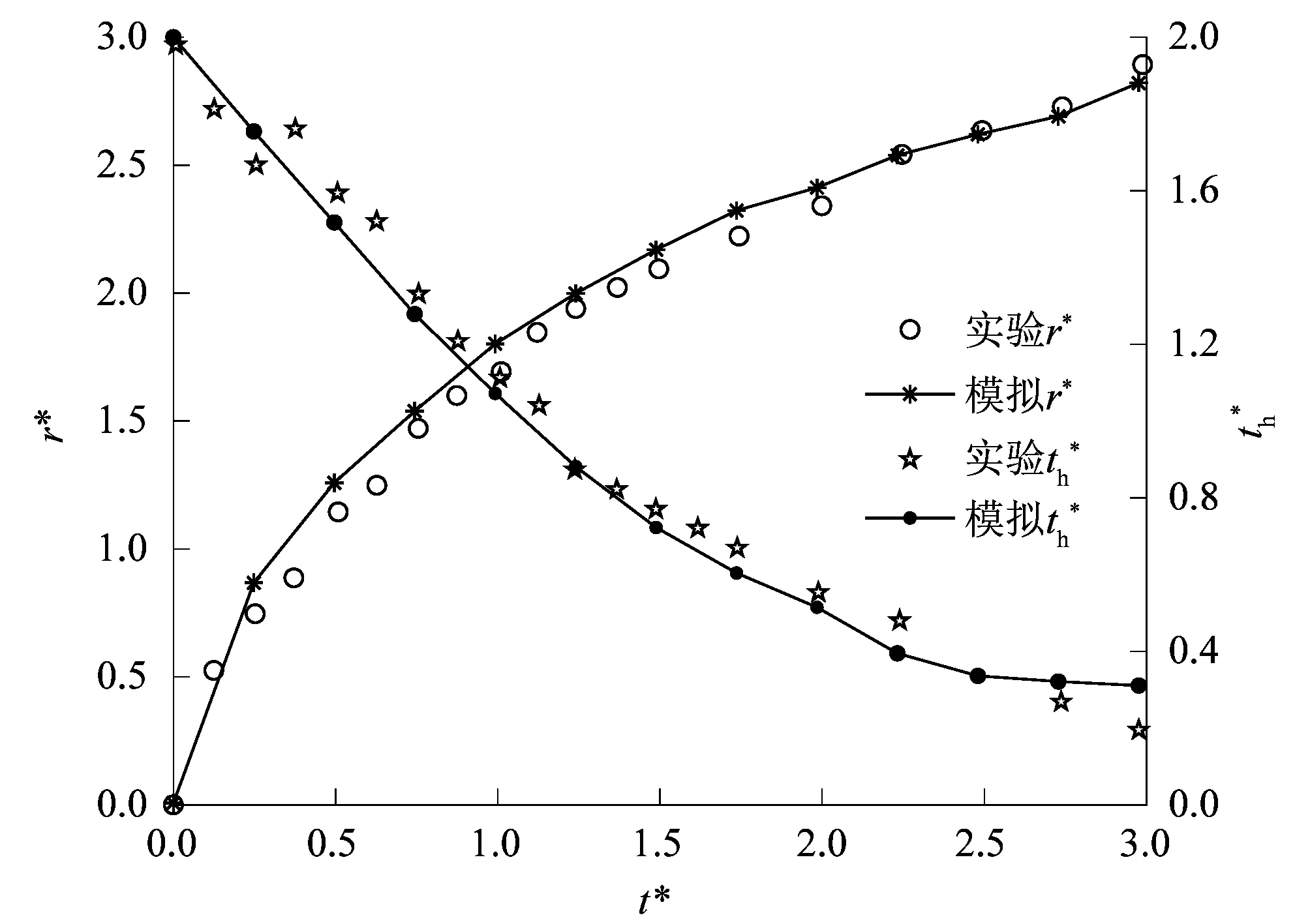
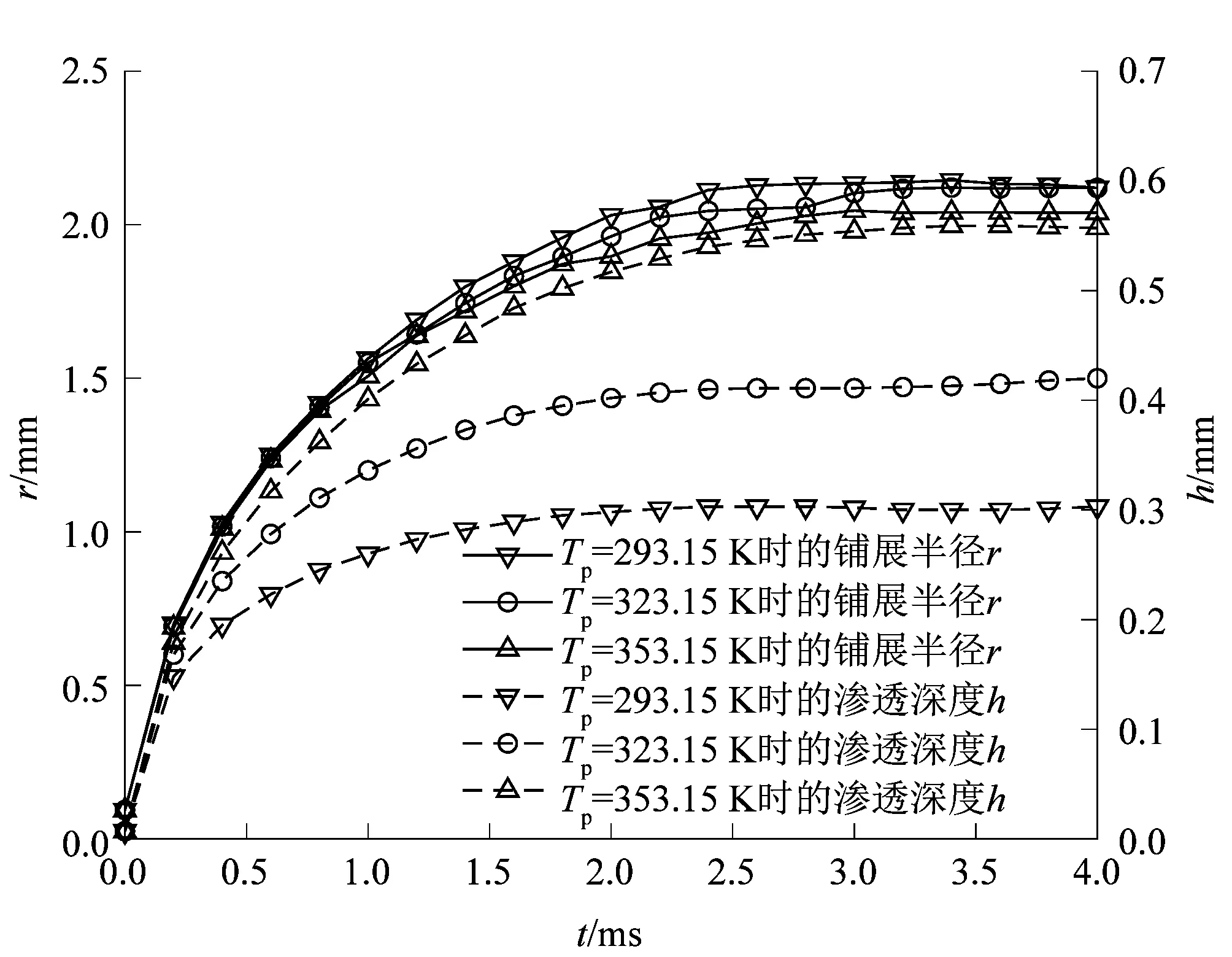
图2 r*和随t*的变化Figure 2 Change of r* and with t*
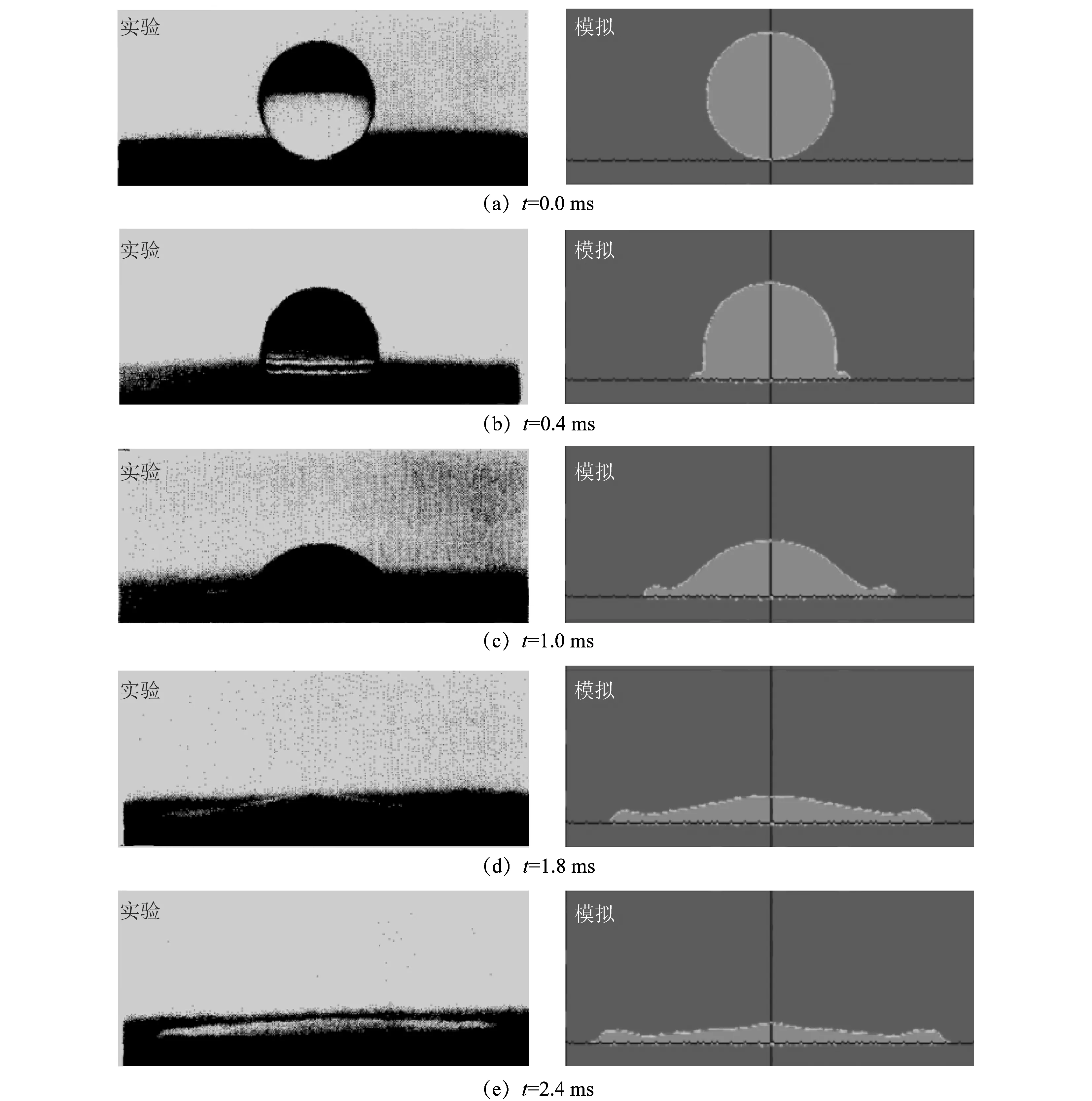
图3 不同时间下实验和模拟液滴变形对比Figure 3 Droplets deformation at different time in experiment and simulation
为验证多孔介质宏观概化模型的准确性,CHANDRA将模拟仿真实验与Chandra的实验结果[15]2385进行了对比。其中,正庚烷液滴的密度ρ=667.5 kg/m3,动力黏度μ=4.05×10-4Pa·s,初始半径r0=0.75 mm,初始速度V0=0.93 m/s,初始温度Td0=295.15 K;陶瓷的孔隙度Φ=0.25,平均颗粒直径dp=7.5 μm;气液表面张力σ=0.020 1 N/m,接触角θ=45°,大气压强pa=0.101 MPa,环境温度Ta=295.15 K。
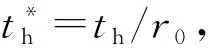
2.2 网格独立性研究
在进行流体仿真模拟实验时,常用库朗数Courant来衡量时间步长Δt与网格尺寸Δx的关系:
Courant=VΔt/Δx。
(11)
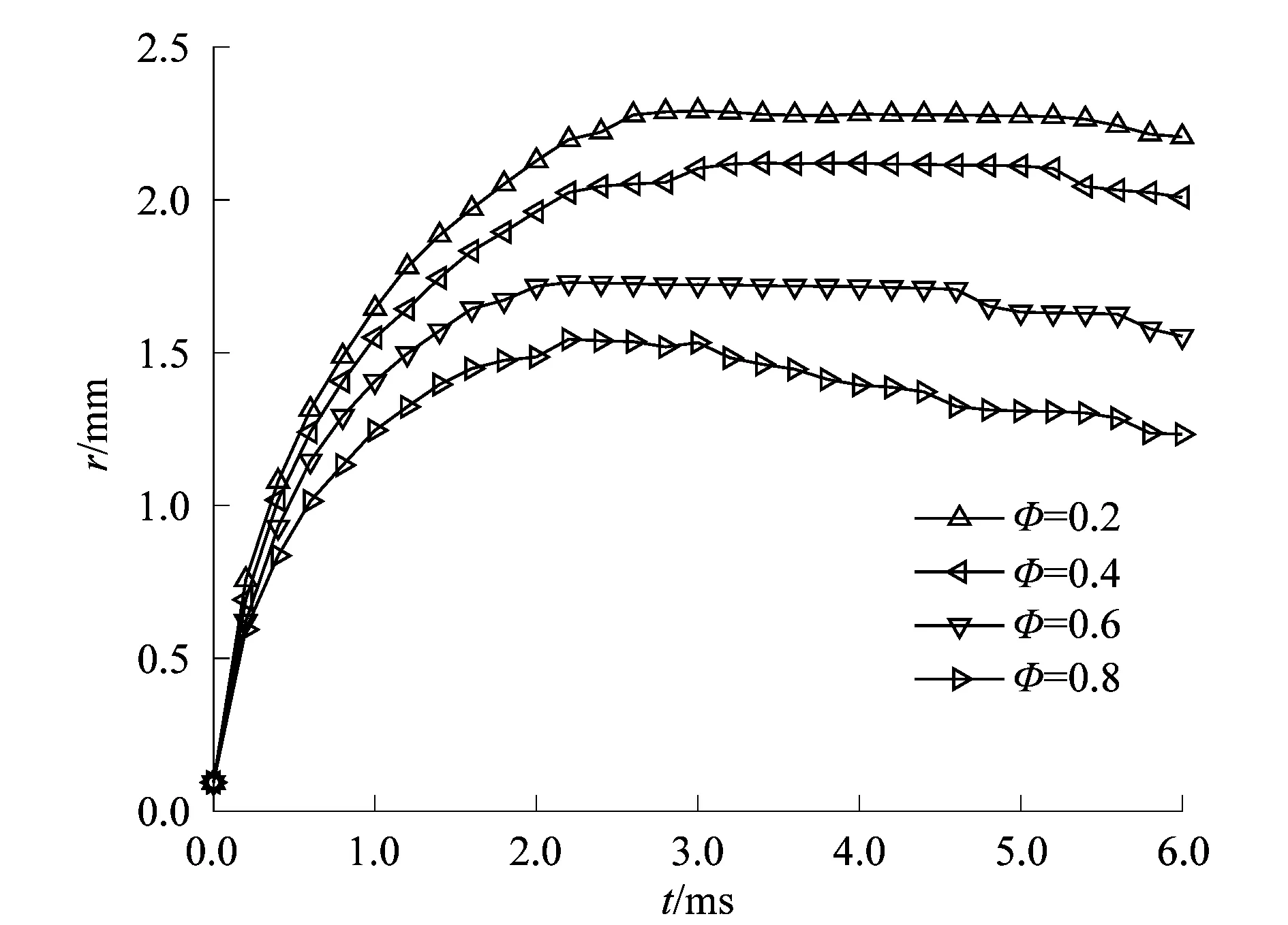
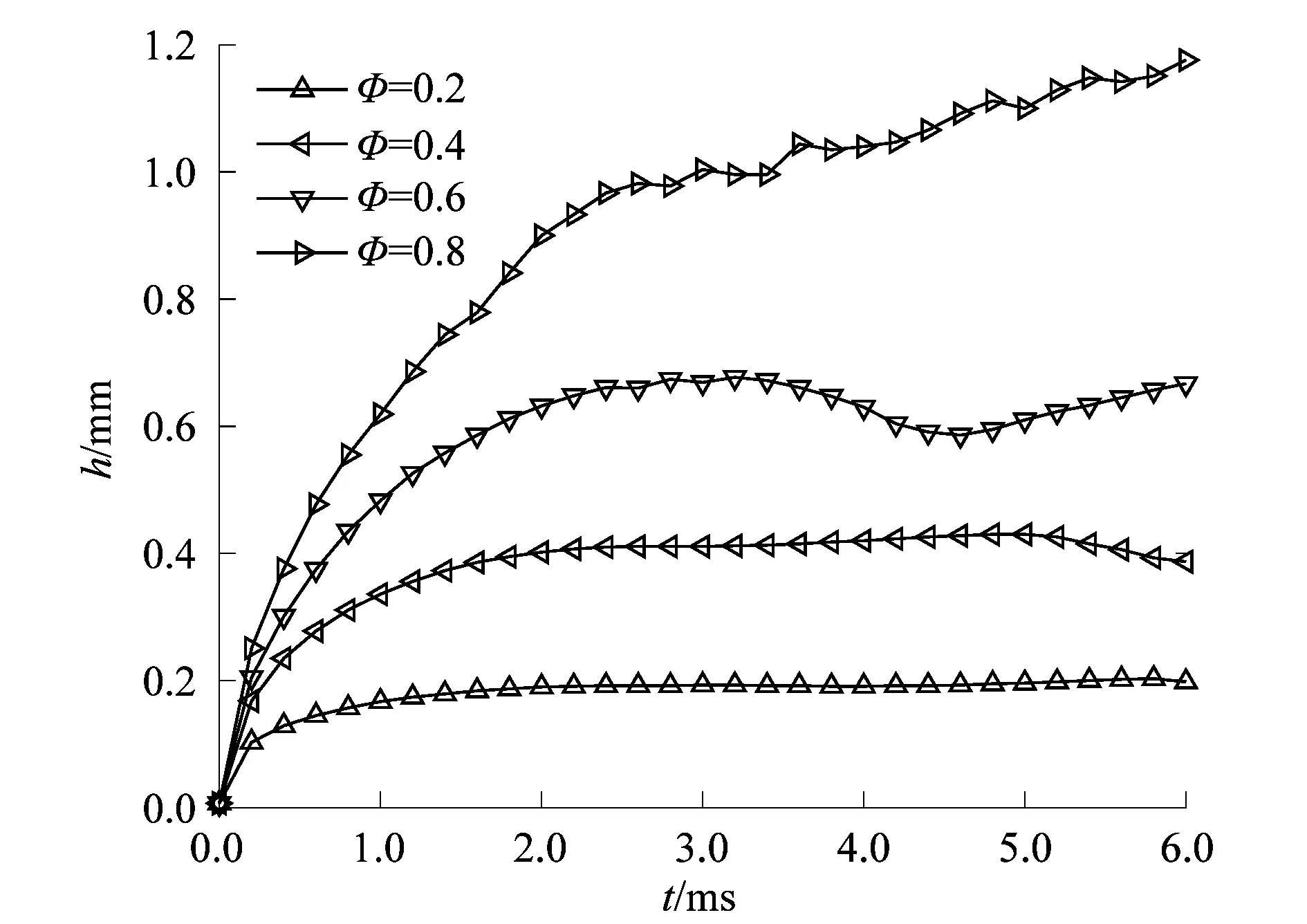
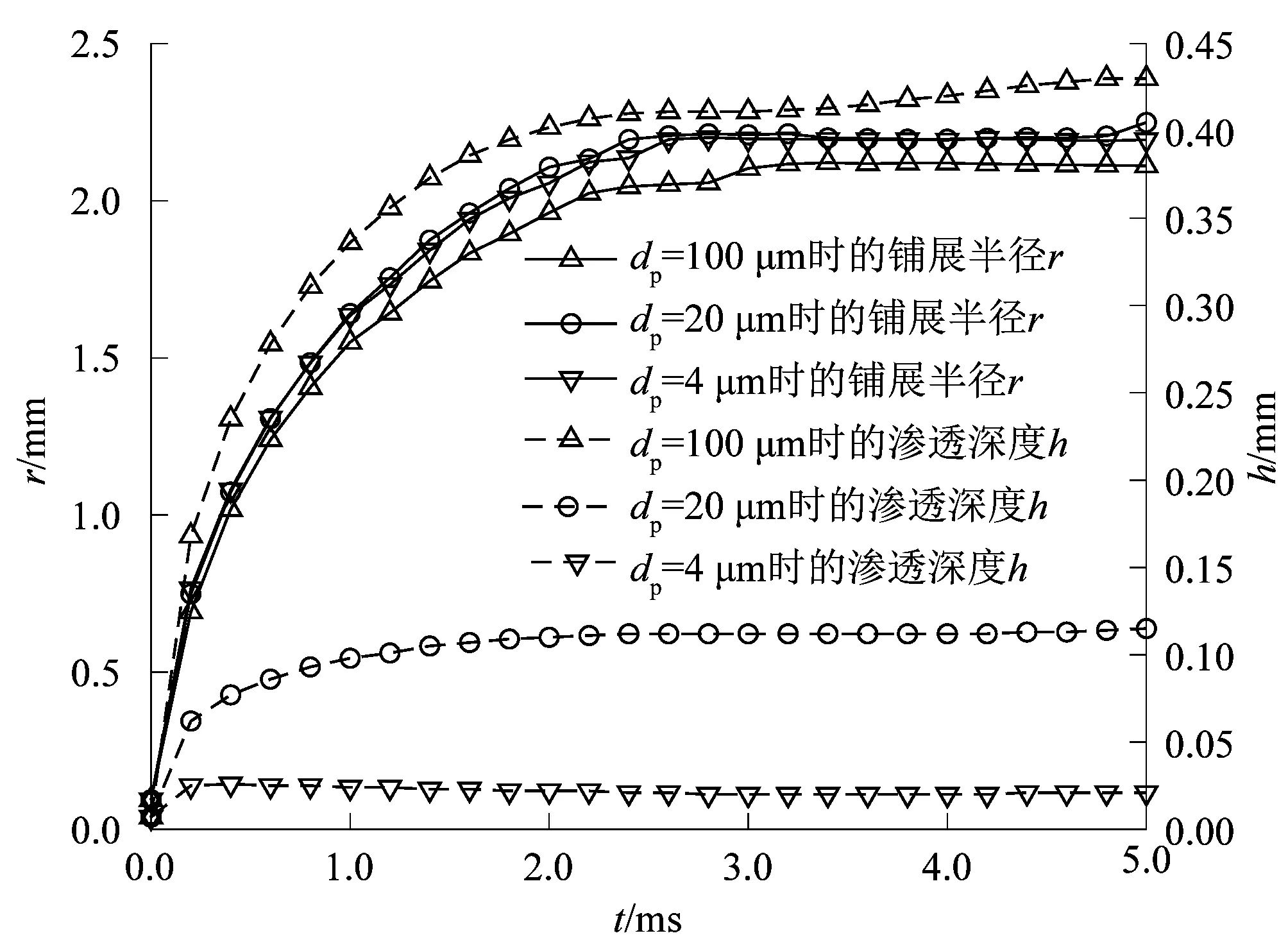
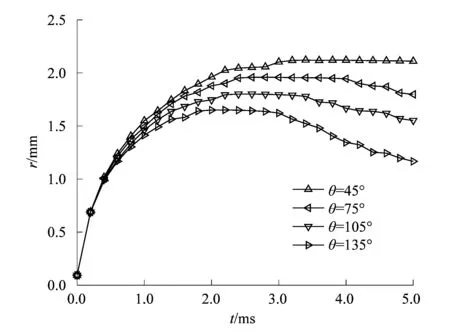
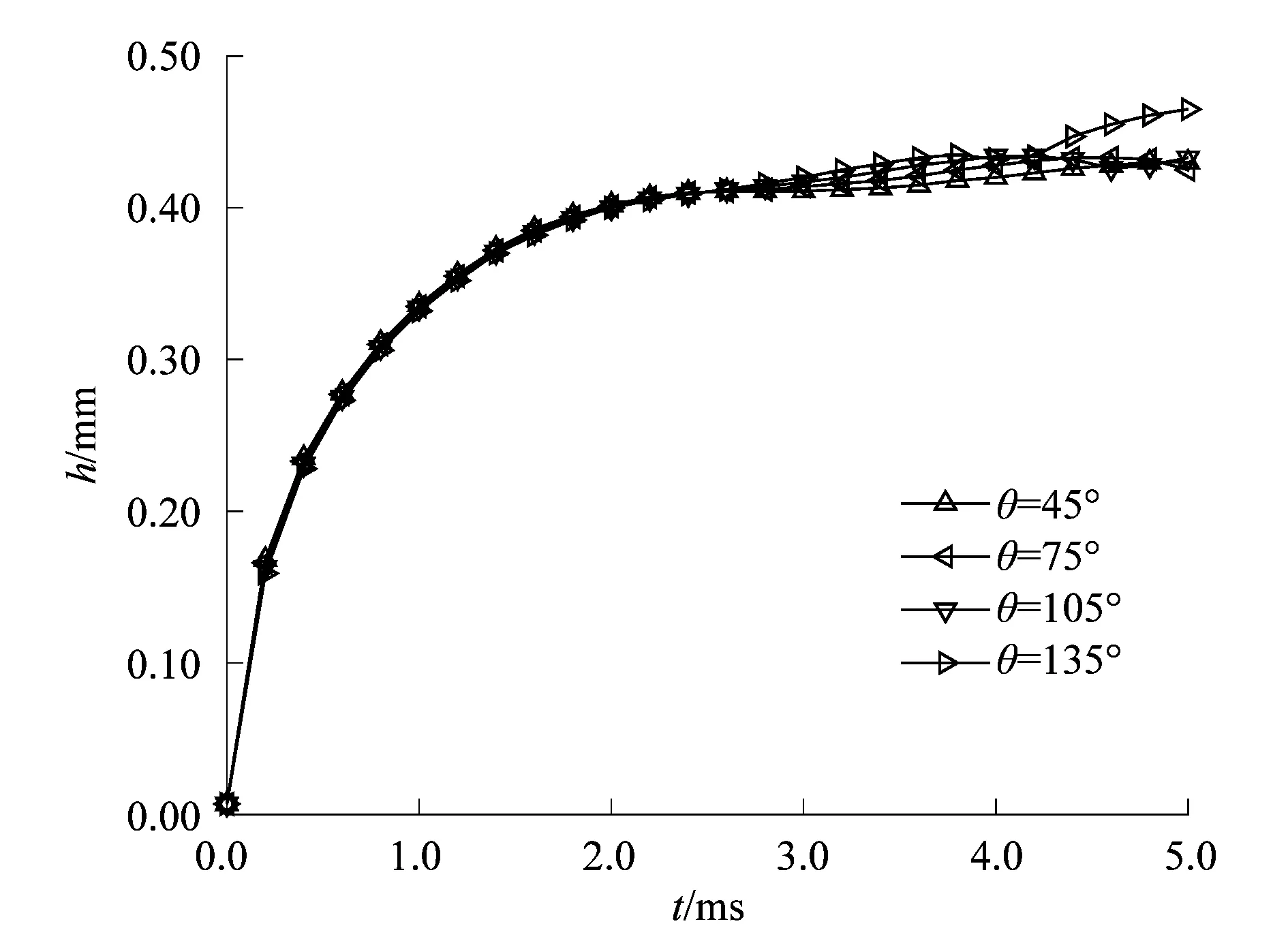
较小的Courant能够增加计算收敛的稳定性,从而保证了求解的精度;较大的Courant能够加快计算收敛的速度,从而降低计算的成本。在保证计算求解的精度的基础上,考虑问题的复杂程度与计算成本,在满足0.05 选取正庚烷液滴撞击陶瓷实验[15]2385中湿润半径r在t=2.4 ms时的结果,对不同网格精度下的模拟结果进行误差分析,结果如图4所示。 图4 网格独立性Figure 4 Independence of grid 从模拟结果中可以发现,随着网格数量的增加,液滴湿润半径r的相对误差不断减小并趋于稳定,在保证精度的基础上为了节约计算成本,最终确定网格数为50 000。 在模拟液滴撞击热多孔介质的实验中,所选用的材料为水、空气和多孔铝板,它们的物性参数如表1所示。 此外,Td0=293.15 K,Ta=293.15 K,表面张力σ=0.072 8 N/m,θ=45°,Φ=0.4,dp=100 μm,Tp=323.15 K,多孔材料表面粗糙度Ra=10 μm。 笔者通过改变恒温多孔材料的表面温度Tp,来观察液滴铺展与渗透的变化趋势,模拟结果如图5所示。 图5 不同Tp下r和h随t的变化规律Figure 5 Change rule of r and h with t for different Tp 从图5中可以发现,随着多孔材料表面温度Tp的升高,液滴的渗透深度h增加,而铺展半径r减小。在对流传热的过程中,流体温度与壁面温度相差越大,则换热量越大。因此,Tp越大,液滴在对流换热的过程中吸热升温也越高。由于液滴的动力黏度μ会随着温度的升高而减小,与此同时,液滴流动时所受到的黏性剪切力和渗透时所受到的黏性阻力也将减小。液滴的铺展与渗透之间是相互竞争的,当多孔材料对液滴的阻力较小时,液滴撞击后所能达到的渗透深度h就越大,而铺展半径r则会相对减小。 孔隙度Φ表示多孔材料内部流体所占据的体积与整个多孔材料占据的总体积之比。笔者通过改变恒温多孔材料的Φ,来观察对液滴铺展与渗透的影响,结果如图6~7所示。 图6 不同Φ下r随t的变化Figure 6 Change of r with t for different Φ 图7 不同Φ下h随t的变化Figure 7 Change of h with t for different Φ 从图6和图7中可以发现,随着孔隙度Φ的增加,液滴的铺展半径r逐渐减小,液滴的渗透深度h则不断增加。根据式(7)和(8)可知,当Φ增加时,多孔材料的渗透率K不断减大,而惯性因子C不断减小;再由式(5)可以发现,随着K的增加,液滴渗透流动时所受到的阻力将不断减小。因此,多孔材料的孔隙率Φ越大,其渗透率K也会增大,液滴的渗透深度h则越深。由于液滴铺展与渗透之间的竞争关系,液滴的铺展半径r随着渗透深度h的增加而减小。 生活中常见的多孔材料是由若干大小不同的颗粒物聚合形成,而颗粒物的大小疏密则影响着多孔材料的渗透吸收性能。笔者通过改变恒温多孔材料的平均颗粒直径dp来观察其对液滴撞击后铺展与渗透行为的影响,结果如图8所示。 图8 不同dp下r和h随t的变化Figure 8 Change of r and h with t for different dp 从图8中可以发现,随着dp的增加,液滴的渗透深度h不断增大,而铺展半径r不断减小。由式(7)和(8)中可知,当dp减小时,多孔材料的渗透率K迅速减小,惯性因子C则不断增大。根据式(5)可知,渗透率K减小,流体渗透进入多孔材料内部所受到的阻力将不断增大。因此,多孔材料的dp越小,液滴的渗透深度h越小,而铺展半径r则越大。 接触角θ可以用来衡量液体在固体表面的铺展润湿能力,根据杨氏方程: σsg-σsl=σglcosθ。 (12) 式中:σsg,σsl和σgl分别为气-固、液-固和气-液表面张力。 当θ>90°时,固体表面表现为疏水状态。本研究通过改变接触角θ的大小,来观察液滴在恒温多孔材料表面的铺展与渗透变化规律,结果如图9和图10所示。 图9 不同θ下r随t的变化Figure 9 Change of r with t for different θ 图10 不同θ下h随t的变化Figure 10 Change of h with t for different θ 从图9和图10可知,接触角θ越大,液滴的铺展半径r越小,而渗透深度h则越深。随着θ的增大,液滴在多孔材料表面湿润性能变差,达到最大铺展半径所用的时间也越短。在表面张力的作用下,液滴回缩后在撞击中心处聚集,底部液滴所受到的压差力也不断增加,促使渗透深度h进一步增大。液滴变形时储藏的表面能随着收缩又转变为液滴的动能,而随着θ的增大,液滴的动能也越大。当θ=135°时,液滴收缩后有了回弹的趋势。 笔者基于液滴润滑理论和多孔介质渗流理论,借助计算流体力学软件FLUENT对液滴撞击恒温多孔介质变形的过程进行了数值模拟研究,其主要结论如下: 1) 恒温多孔材料的表面温度Tp越高,液滴撞击时吸热升温越快,多孔材料对液滴的阻力也就越小;因此,Tp越大,液滴的渗透深度h越大,而铺展半径r越小。 2) 恒温多孔材料的孔隙率Φ越大,其渗透率K也越大,液滴所能达到的渗透深度h增加,而铺展半径r则会随着h的增加而减小。 3) 恒温多孔材料的平均颗粒直径dp越小,其渗透率K也越小,渗透性能越差;因此,dp越小,液滴的铺展半径r越大,渗透深度h越小。 4) 随着接触角θ的增加,液滴在恒温多孔材料表面的湿润性能变差,铺展半径r不断减小,而渗透深度h则会相对增加。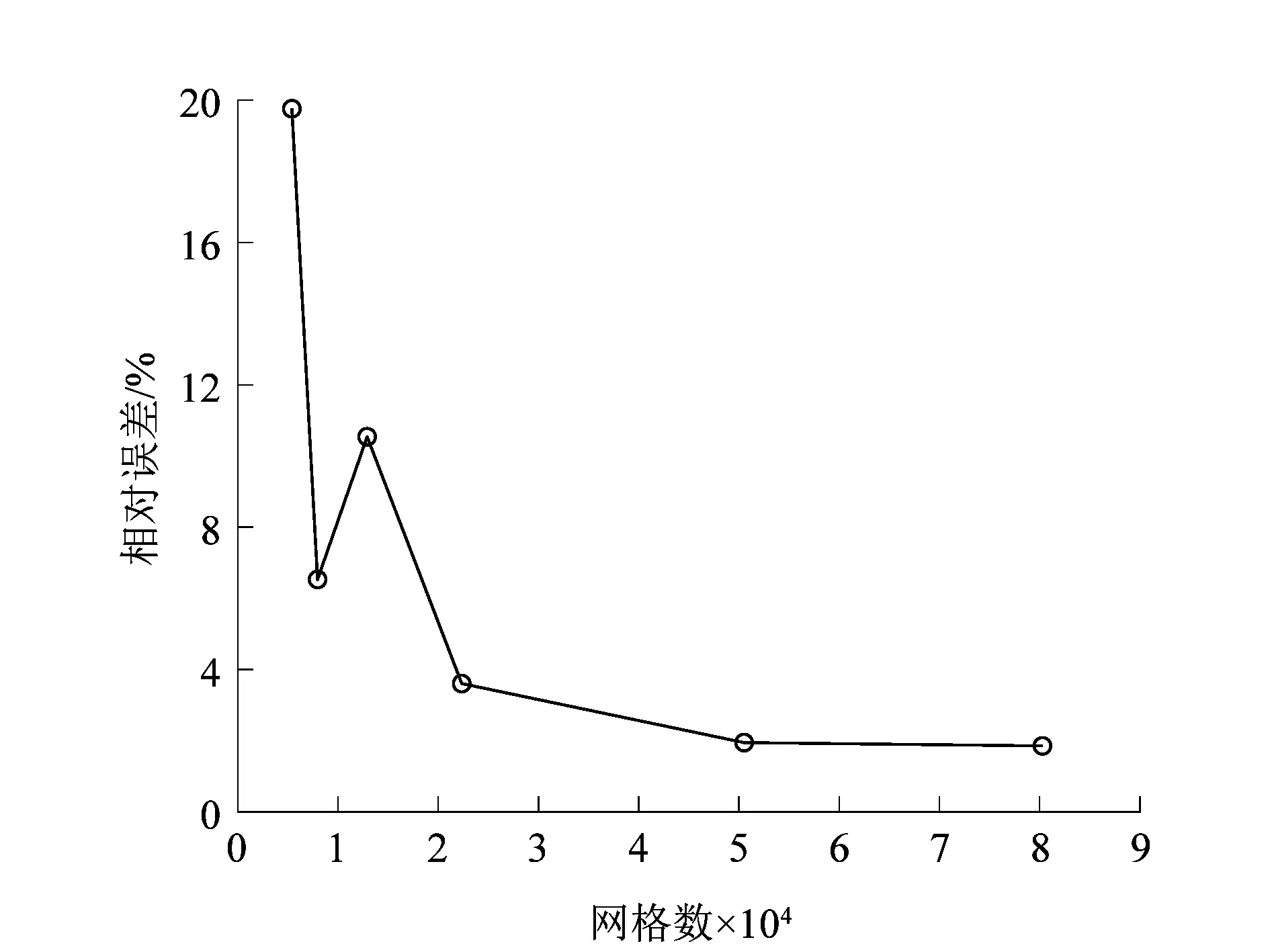
3 参数分析
3.1 表面温度的影响
3.2 孔隙度的影响
3.3 平均颗粒直径的影响
3.4 接触角的影响
4 结论

