剪切流作用下层合梁非线性振动特性研究1)

刘昊 瞿叶高 孟光

(上海交通大学机械系统与振动国家重点实验室,上海 200240)

引言

轴向流动下弹性梁或板结构的稳定性问题是流固耦合动力学中经典的问题之一,广泛存在于航空工程、海洋工程、核能工程[1-3]等领域.置于流场中前缘固支的柔性梁或板状结构在来流速度超过临界流速时,会产生周期性的大挠度自激振动现象,这种振动现象可以归因于运动诱发激励机制(movementinduced excitation,MIE)[4].

国内外针对均匀轴向流中柔性梁或板结构振动问题开展了一些研究.早期Taneda[5]基于实验方法研究了旗帜的各种振动模式.Eloy 等[6]采用稳定性分析方法分析了轴向流中悬臂柔性板的周期性极限环振动和混沌振动机制.Zhu 和Peskin[7]采用浸入边界法研究了细丝在流动的肥皂膜中的振动现象,揭示了更长的细丝向不稳定振动模式的过渡和双稳态区域的存在.文献[8]采用基于有限差分格式的直接模拟(fluid-structure direct simulation,FSDS)方法,以质量比为变量,分析了均匀流作用下柔性板的振动特性.Lui 等[9]提出CEFI (combined field with explicit interface)公式,采用有限元方法分析质了量比和雷诺数的改变对柔性板振动特性的影响.Zhang 等[10]采用一种松耦合格式研究了强附加质量效应下二维柔性板的流致振动现象.以往的研究[11-12]揭示了均匀流作用下柔性板具有三种不同的变形模式:定点稳定模式、周期性极限环振动模式以及混沌振动模式.最近,Saravanakumar 等[13]开展了复合材料层合梁在均匀流中的振动特性研究,分析了铺层刚度和密度对层合梁振幅、频率和涡脱落模式的影响.

实际工程中存在很多剪切流流场,而剪切流动作用下弹性结构的流固耦合动力学行为更加复杂.Cheng 等[14]采用LBM (lattice boltzmann method)方法分析了作用在圆柱和方柱上的二维不可压缩线性剪切流.结果表明,圆柱后的涡结构与剪切速率有很大关系,作用在圆柱上的升力和阻力一般随剪切速率的增大而减小,通过方形圆柱的涡流脱落频率随剪切速率的增大而减小.Yu 等[15]采用高精度谱方法研究了剪切流对NACA0012 翼面上涡结构的演变及相应的气动性能的影响.Liu 等[16]研究了水翼在不同剪切速率的剪切流作用下振动的能量收集效率问题.文献[17-18]对二维线性剪切来流作用下弹性支撑圆柱体结构物双自由度流致振动问题进行了数值计算,发现圆柱在剪切流中的运动轨迹呈液滴形状,这与均匀流的“8”形轨迹明显不同.

复合材料弹性结构已广泛应用于船舶舰艇、海洋工程等领域结构设计[19-20].研究剪切流动作用下复合材料层合梁振动机制对于上述领域结构设计具有重要的意义.关于单层梁在均匀流作用下的振动已经开展了大量研究,但对于复合材料层合梁在剪切流作用下的振动研究较少,剪切流分布、层合材料的差异对于振动特性的影响和机理尚不清楚.本文针对水下剪切流动下复合材料层合梁振动问题,基于复合材料层合梁高阶剪切锯齿理论[21-23],建立了不可压缩黏性剪切流中层合梁高精度的非线性流固耦合动力学数值模型,研究了不同剪切流动下不同刚度比、不同铺层厚度、不同铺层角度层合梁的大变形非线性振动行为与机理.本文为水下剪切流动作用下复合材料梁的动力学响应预测和复合材料结构设计提供参考依据.

1 模型描述

1.1 计算模型

本文考虑一个沉浸在水中的复合材料层合梁,层合梁的长宽尺寸为L×H,H=0.01L,其几何中心距流体域左边界距离为2L,到右边界距离为10L,到流体域上下边界的距离均为2L,如图1 所示.不考虑流体和结构所受的重力.将水介质假设为不可压缩黏性流体,流体密度为 ρf,动力黏度为 µf.左端入口处的剪切流速度分布函数为U(Y)=U0(Y/2L)α,层合梁中轴线处的流速为U0,对应的雷诺数为Re=ρf U0L/µf.

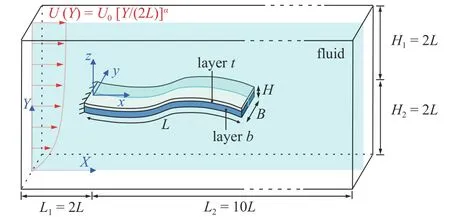
图1 计算模型Fig.1 Computational model

1.2 边界条件

浸没在流体中的层合梁前端(x=0)固支,右端(x=L)自由.流场区域的左端入口采取流速的边界条件:u=U(Y),v=0 ;右端出口设置压力出口边界条件:p=0 ;层合梁结构表面为流固耦合界面,设置无滑移边界条件;流域上下边界设置为滑移固壁边界条件:∂u/∂y=0,v=0 .

2 流固耦合建模与计算方法

2.1 流体数值计算模型

不可压缩黏性流体的控制方程为Navier-Stokes方程,本文采用ALE (arbitrary Lagrangian Eulerian)方法描述流体网格的变形.在ALE 框架下,流体控制方程为[24]

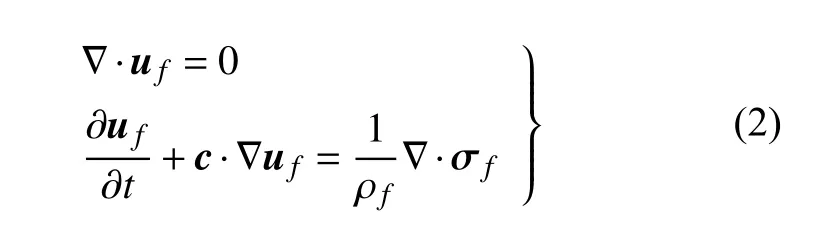
其中,uf是流体速度矢量，ρf表示流体密度,c是ALE 速度矢量c=uf−um,um表示流体网格变形速度.将水介质假设为不可压缩牛顿流体,应力张量σf定义为

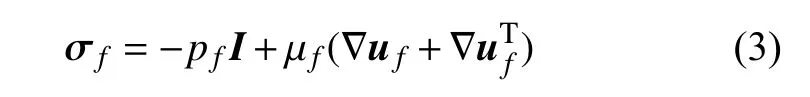
采用有限体积法对流体控制方程进行离散[25],任意一个控制体单元内的离散方程可以表示为

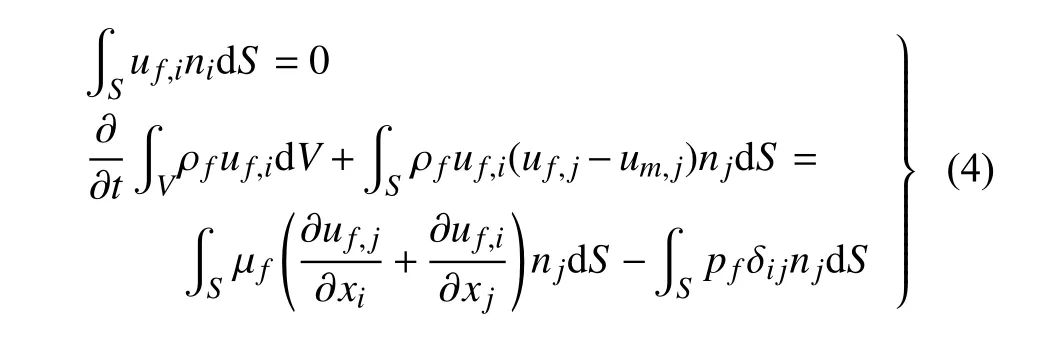
其中,V代表控制体体积,S代表控制体表面积,nj是控制体表面的单位法向向量,um,j表示控制体j方向的网格变形速度.时间离散采用二阶隐式欧拉方法,对流项离散采用线性迎风差分方法,扩散项离散采用中心差分方法,速度和压力耦合项采用PIMPLE(PISO-SIMPLE)算法[26]求解.

2.2 层合梁结构动力学数值模型

基于考虑层合梁面内位移锯齿效应的高阶剪切梁锯齿理论来描述层合梁的振动变形.层合梁内任意一点P(x,z)在x和z方向的位移可以表示为[27]

其中,u,w,ϑ 和 η 表示层合梁中性轴上的广义位移,仅与坐标x和时间t有关.f(z)和g(z) 是广义位移分布形函数,反映了位移沿厚度方向的分布情况,其表达式为[28]

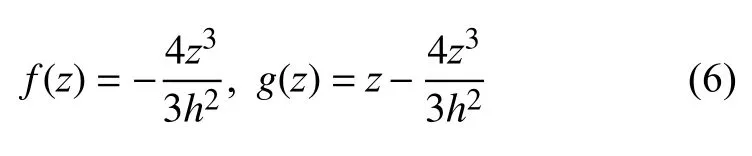
式(5)中 φ (z,k) 是锯齿函数(zig-zag 函数),与坐标z及铺层数目k有关,定义为[29]

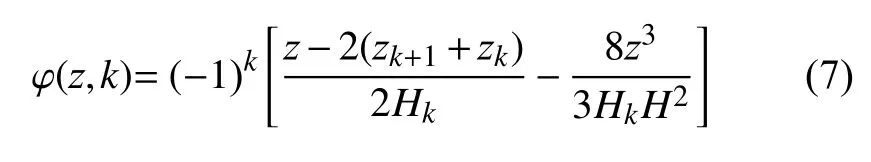
基于von Kármán 位移−应变关系来考虑层合梁的几何非线性大变形效应.层合梁的应变分量表达式为

忽略层合梁厚度方向的正应力和正应变,正交各向异性材料铺层的应力应变关系如下[30]

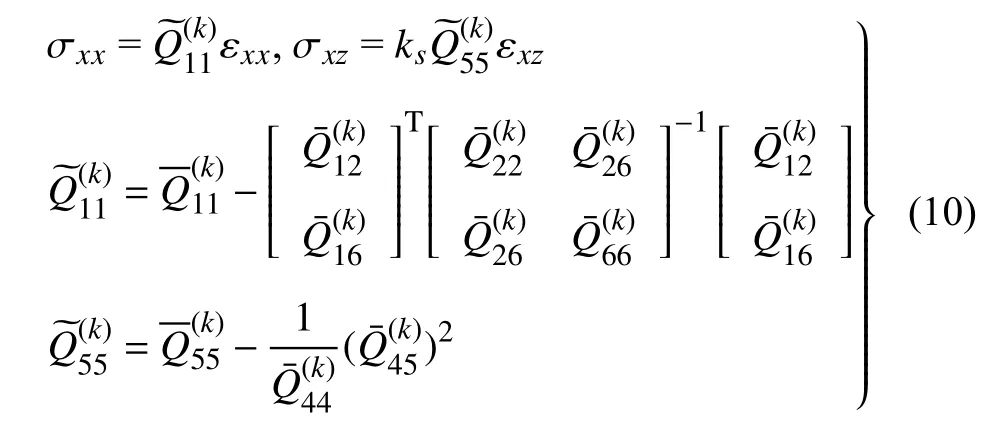
采用有限元方法对层合梁的运动方程进行离散,采用2 节点10 自由度梁单元对层合梁进行离散,对轴向位移分量u和广义位移变量ϑ,η 采用线性插值,对横向位移分量w采用Hermite 函数进行插值.层合梁非线性振动有限元方程可写为[30]

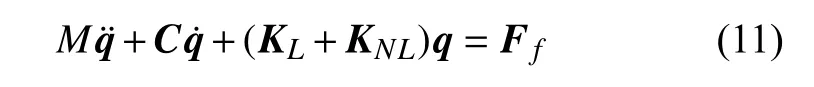
式中,M表示层合梁的质量矩阵,KL和KNL分别表示层合梁的线性和非线性刚度矩阵,C是阻尼矩阵,动力学分析中一般采用瑞利阻尼描述.Ff为外部流场载荷向量.

采用直接积分Newmark-β方法结合Newton-Raphson 迭代方法对层合梁结构的非线性振动有限元方程进行求解.在每个时间步长内,需要根据层合梁与流体的耦合作用来迭代计算Ff.

2.3 双向流固耦合算法

考虑流体与层合梁的强耦合作用.在流体与结构耦合界面上,需要满足力平衡条件和速度协调条件

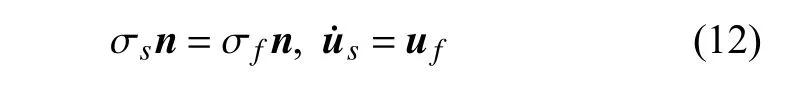
式中,n为流固耦合界面的单位法向量,为流固耦合界面处结构的速度.

本文采用分区流固耦合计算方法来迭代求解流动响应和结构振动响应,如图3 所示.由于流体和结构网格是非匹配的,需要对流体域计算后获得的流固耦合界面力ff si=FΓ进行插值计算,将其作为层合梁的外载荷Ff.对于不可压缩牛顿流体,边界上的力Ff可由Cauchy 应力张量与表面法向向量的内积,再乘以表面面积得到[26]

图2 复合材料层合梁的示意图Fig.2 Schematic diagram of composite laminated beam

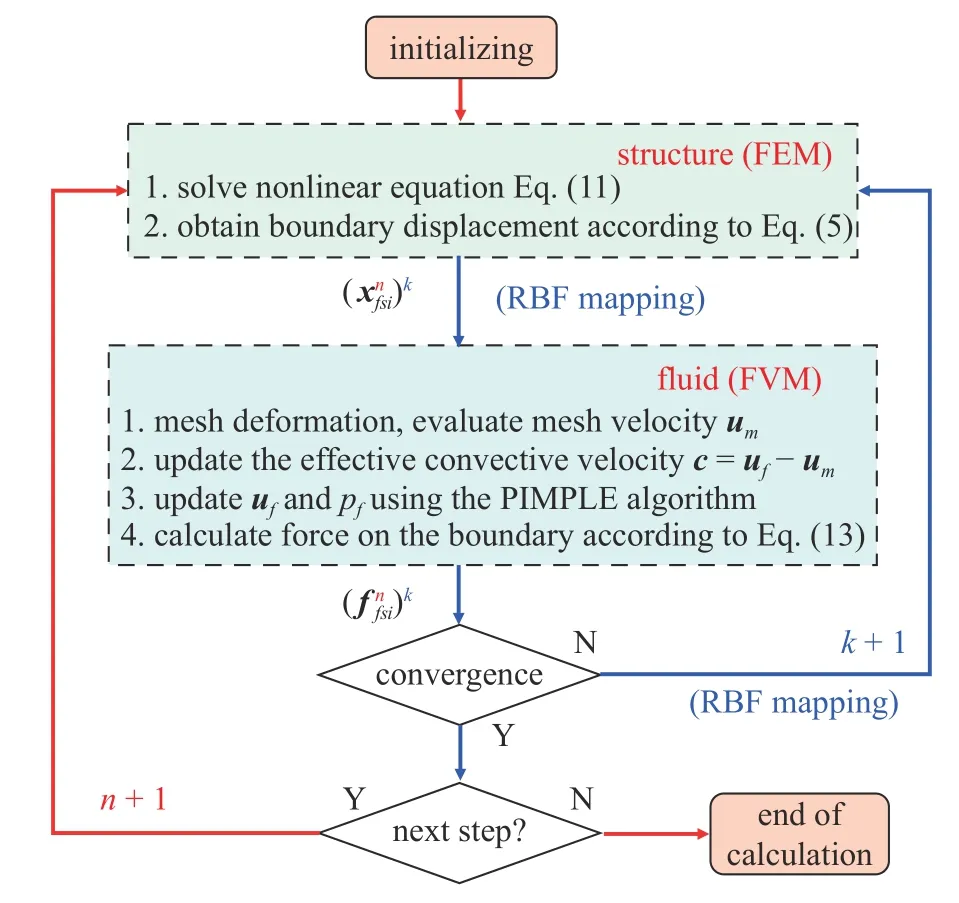
图3 双向流固耦合计算流程图Fig.3 Flowchart of bidirectional fluid-structure interaction

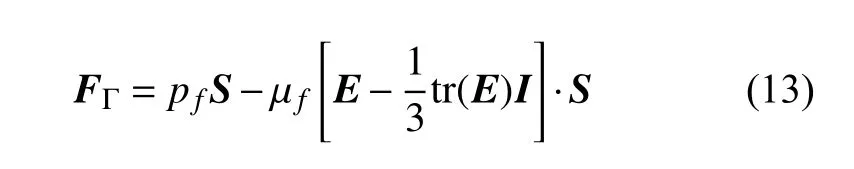
结构在流场载荷作用下产生振动变形,更新结构位移xf si=us,将其插值后传递给流场作为下一个耦合迭代步流场的运动边界条件.在一个时间步内进行多次耦合迭代,直到流场、结构以及流固耦合界面都达到设定的力收敛和位移收敛准则,程序再推进下一时间步计算.本文采用径向基函数(radial basis functions,RBF)[31]方法对流固耦合界面上流场和结构非匹配节点的物理量数据进行插值.

3 数值计算和结果分析

3.1 算例验证

采用不同数目网格来分析层合梁(∆=0)在均匀流作用下的振动响应收敛特性.采用3 节点三角形非结构单元对流体区域进行离散,采用2 节点梁单元对层合梁进行空间离散.考虑了三种计算网格:Mesh A (NE=11860,NP=6109,NM=50)、Mesh B(NE=19426,NP=10220,NM=60)和Mesh C (NE=41624,NP=21184,NM=80),其中NE表示流场单元数,NP表示流场节点数,NM表示梁单元数目.图4给出了网格C 对应的流场非结构网格,层合梁的表面布置三层边界层网格,其中第一层网格高度根据无量纲壁面距离y+=1 计算得到.三种网格得到的层合梁无量纲振幅uy/L和无量纲振动频率f L/U0如表1所示,表中还给出了文献[13]数值计算得到的结果.结果表明,由Mesh C 网格得到的层合梁振动幅值与文献[13]结果之间的最大偏差为2.4%,后续的数值计算采用网格C.

图4 流场非结构网格C Fig.4 Overview of the Mesh C

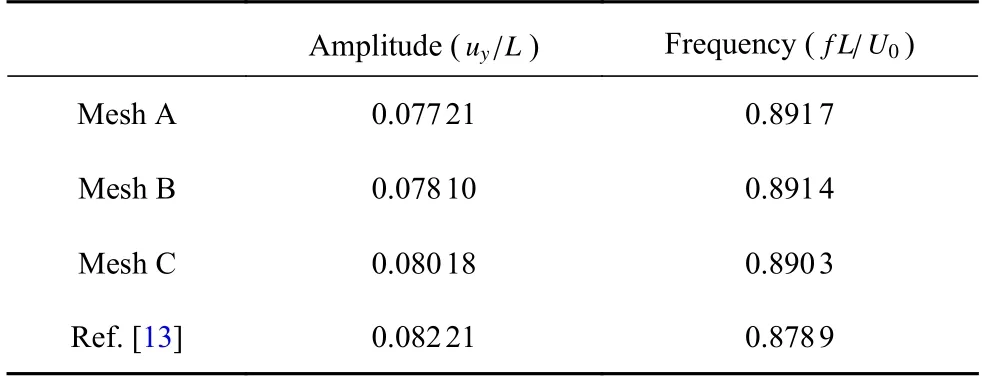
表1 网格收敛性分析Table 1 Grid independence test

考虑层合梁不同铺层弯曲刚度之差 ∆ 情况下,分析层合梁上下两层弹性模量的差异对层合梁振动响应的影响.图5 和图6 给出了10 个无量纲时长内,层合梁右端(x=L)节点振动最大幅值和主导频率随铺层弯曲刚度之差的变化.图中还将本文数值计算结果与文献[13]的结果进行对比.结果表明,层合材料的差异对梁的振动响应具有显著影响,随着 ∆ 的增加,层合梁振动幅值增大,主导频率有下降的趋势.需要指出,文献[13]基于CEFI 公式[9],采用有限元方法统一求解流体和结构,层合梁的非线性建模采用了Saint Venant Kirchhoff线性超弹性材料和Green-Lagrangin 位移−应变关系.而本文采用分区强流固耦合方法,流体部分采用有限体积法求解,结构部分采用有限元方法求解,层合梁的几何非线性建模采用von Kármán 位移−应变关系,导致本文计算得到的层合梁振幅和频率结果与文献解略有差别.

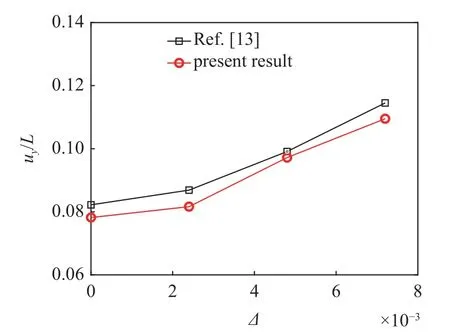
图5 不同 ∆ 情况下,层合梁右端(x=L)节点横向位移的最大振幅Fig.5 Maximum amplitude of transverse displacement at laminated beam tip as a function of ∆

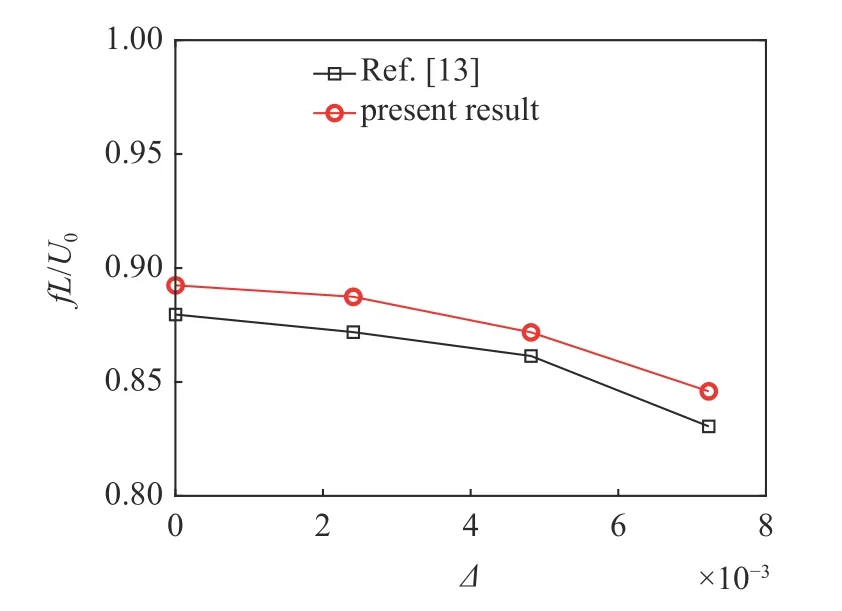
图6 不同 ∆ 情况下,层合梁右端(x=L)节点横向位移的主导频率Fig.6 Dominant frequency of transverse displacement at laminated beam tip as a function of ∆

3.2 剪切流速度分布对单层梁振动的影响

本节研究剪切流的速度分布对单层梁振动特性的影响.考虑剪切流不同的来流速度分布 α ∈[0,2],采用如下无量纲参数:Re=1000,αavg=10,βavg=6000,h=0.01.来流速度分布与系数 α 的关系如图7 所示.

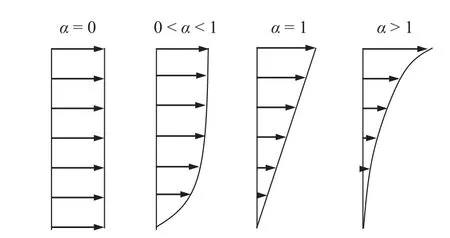
图7 不同 α 情况下的来流速度分布Fig.7 Velocity profile as a function of α

图8 给出了剪切流中单层梁右端节点10 个运动周期的横向位移标准差和平均值随 α 变化的曲线.图9 给出了振动频率随 α 变化的曲线.结果表明,随着剪切流速度分布系数 α 的增加,单层梁振动的幅度和主导频率(涡脱落频率)均是先减小后增加,单层梁的振动平均值随着 α 的增加逐渐增大,振动的向下偏斜更加明显.

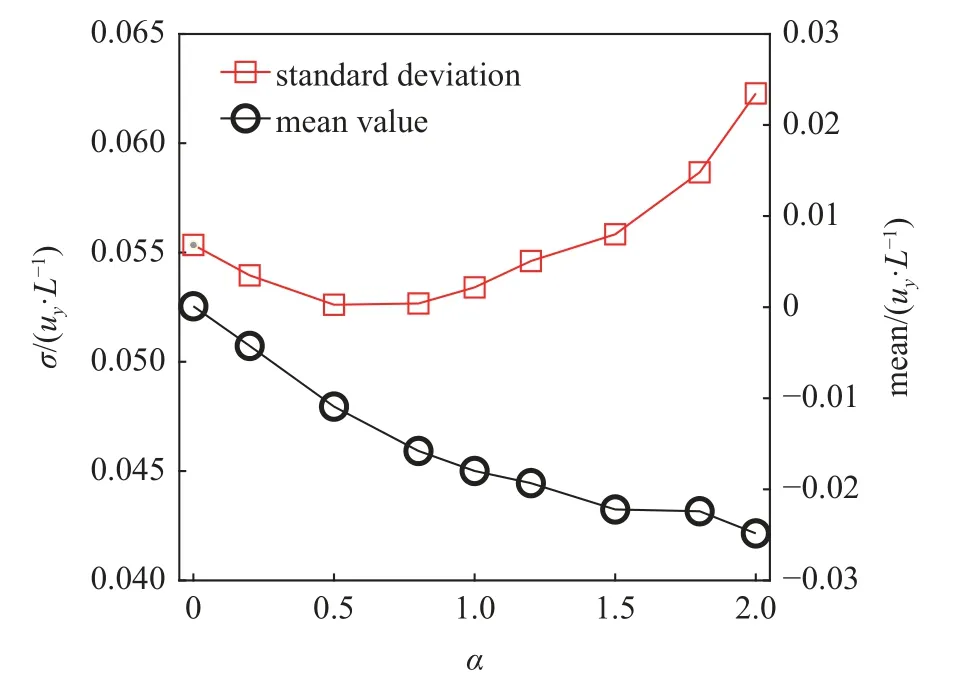
图8 单层梁右端(x=L)节点的横向位移标准差曲线和平均值曲线Fig.8 Standard deviation and mean value of transverse displacement at single isotropic beam tip as a function of α

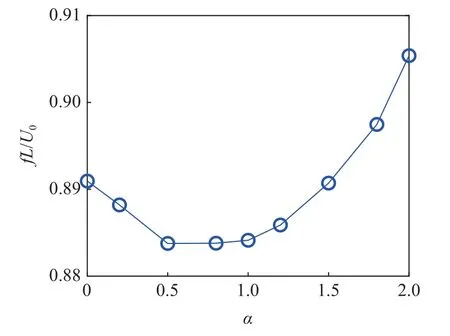
图9 单层梁右端(x=L)节点的横向振动频率曲线Fig.9 Dominant frequency of transverse displacement at single isotropic beam tip as a function of α

图10 给出不同 α 情况下单层梁在一个完整运动周期内的变形包络图,红色虚线为中性轴,图10(c)标记了单层梁拍动过程中弯曲变形的三个拐点(x4=0.175L,x4=0.475L,x3=0.775L) 和右端节点x4=L.图11 给出了 α=1 情况下上述四个节点在5 个振动周期内的横向位移时域曲线,位移曲线峰值的依次出现表明单层梁的振动模式区别于类模态振动模式,是一种行波形式的振动模式[32].图12 给出不同 α 情况下,20 个振动周期内,单层梁右端节点位移的Lissajous 曲线,红色虚线表示横向位移的平均值.结果进一步表明,随着剪切流速度分布系数 α的增加,单层梁的振动平均偏斜量增加,右端节点的运动轨迹发生改变,当 α=2 时(图12),Lissajous 曲线的不对称性变得明显.

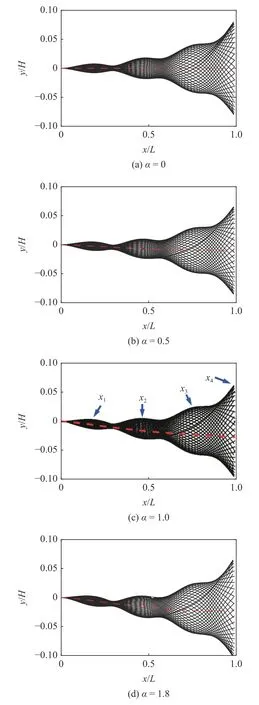
图10 单层梁在一个完整振动周期内的变形包络图Fig.10 Deformation envelope of single isotropic beam in a complete motion period

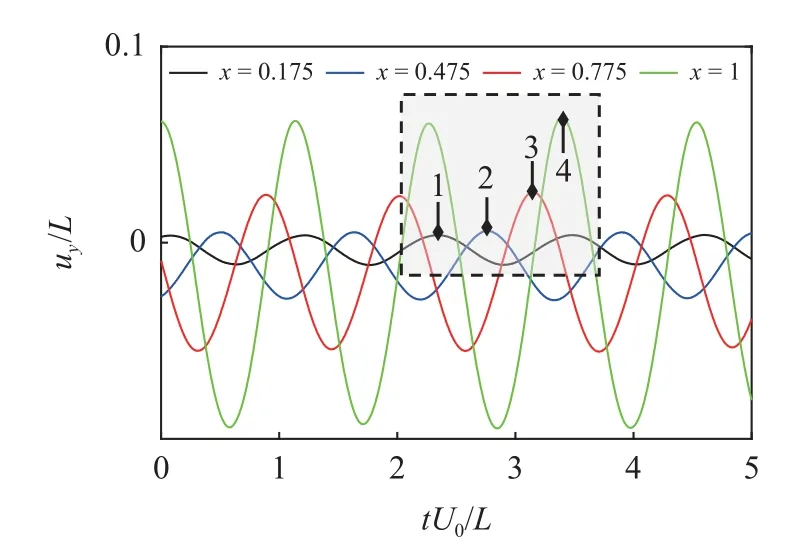
图11 单层梁不同位置节点在5 个振动周期内的横向位移时域曲线(α=1)Fig.11 Time domain responses of transverse displacement of beam at different positions in 5 flapping motion periods (α=1)

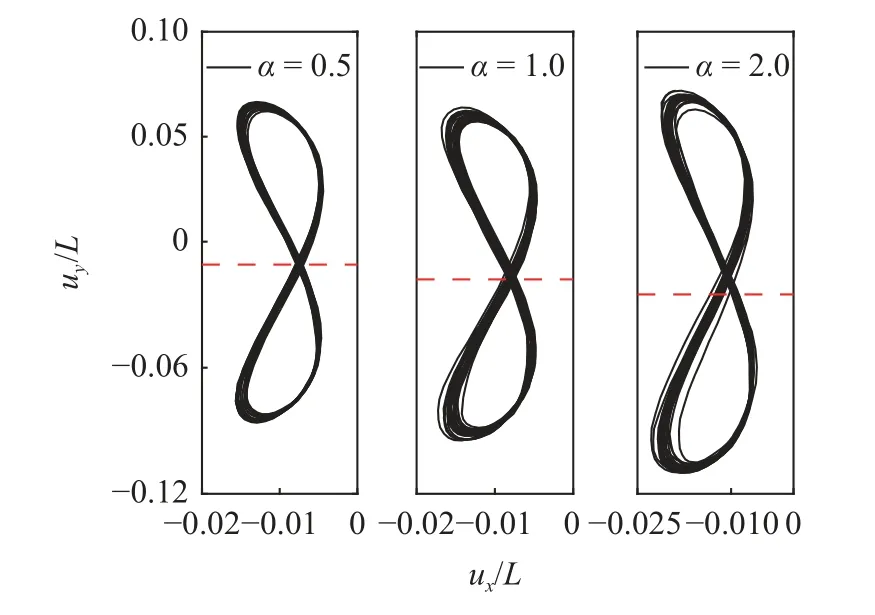
图12 不同 α 情况下,单层梁在20 个完整振动周期内的右端节点位移Lissajous 曲线Fig.12 Lissajous curves of single isotropic beam in 20 flapping motion periods at beam tip with different α

图13～图15 分别给出了剪切速度分布 α=0,α=0.5,α=1.8 情况下,单层梁一个完整振动周期内的流场涡量图.在α=0 情况下观察到典型的2 S 涡模态(每个振动周期脱落两个单独的涡,两个涡的强度几乎相等,旋转方向相反);随着剪切速度分布系数 α 增加,单层梁后方流场中脱落的漩涡不再呈现对称趋势,在α=0.5 和 α=1.8 情况下,上方的漩涡尺寸较大且形状较圆,下方的漩涡尺寸较小且形状较细长.

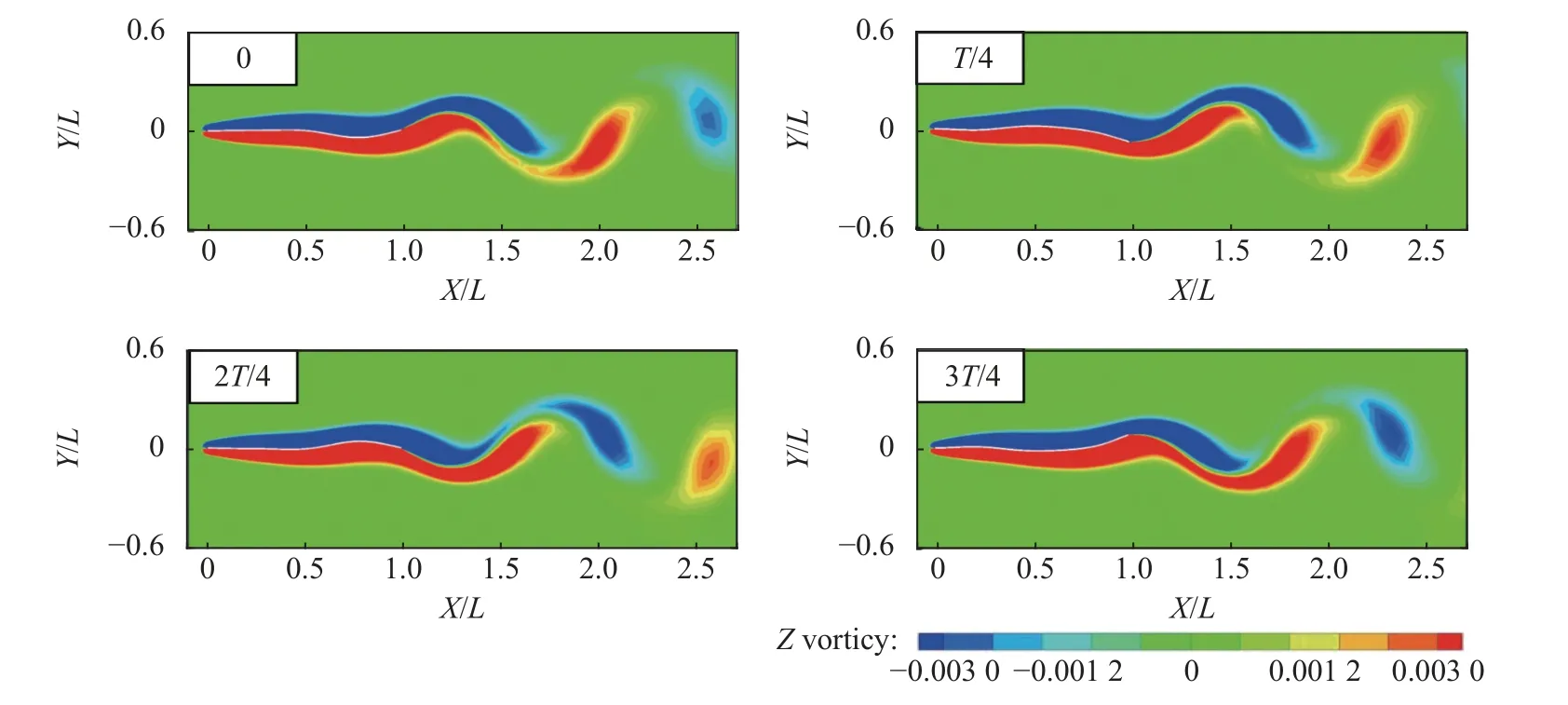
图13 一个完整振动周期内的涡量图(α=0)Fig.13 Vorticity diagrams in a complete flapping motion period at α=0

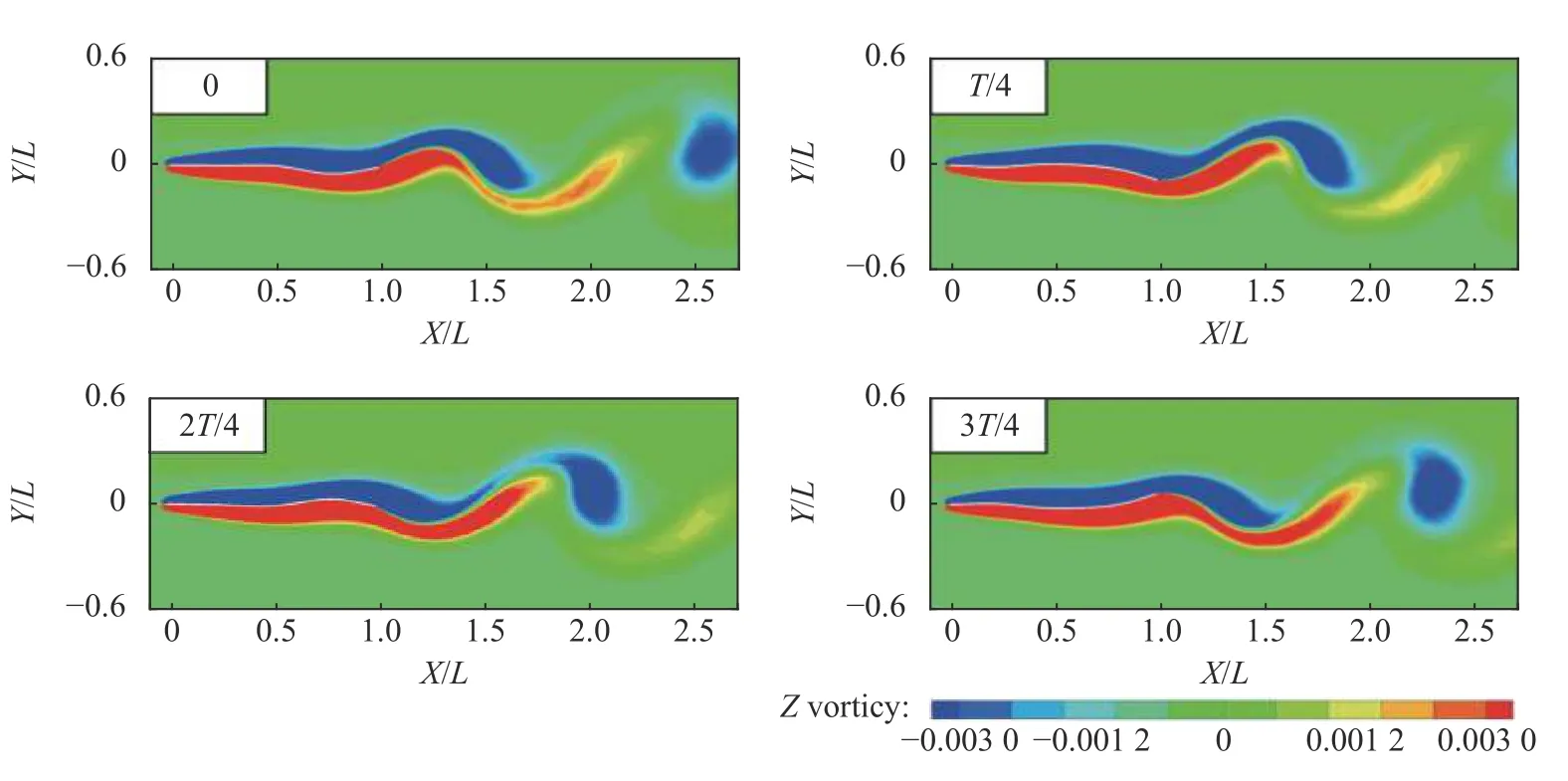
图14 一个完整振动周期内的涡量图(α=0.5)Fig.14 Vorticity diagrams in a complete flapping motion period at α=0.5

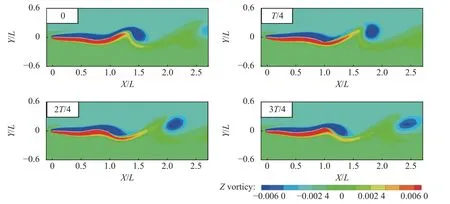
图15 一个完整振动周期内的涡量图(α=1.8)Fig.15 Vorticity diagrams in a complete flapping motion period at α=1.8

3.3 刚度比对剪切流中层合梁振动的影响

本节研究剪切流中层合梁上下两层弹性模量的差异对振动响应的影响,考虑不同刚度比 ∆=2.4 ×10−3,4.8 × 10−3,7.2 × 10−3,9.6 × 10−3.图16 给出了10 个无量纲时长区间内,不同刚度比的层合梁右端(x=L)节点的横向位移时域曲线,可以发现随着刚度比 ∆ 的增加,双层层合梁振动的振幅增大,主导频率下降,这一规律与均匀流作用下层合梁的振动特性变化规律一致.

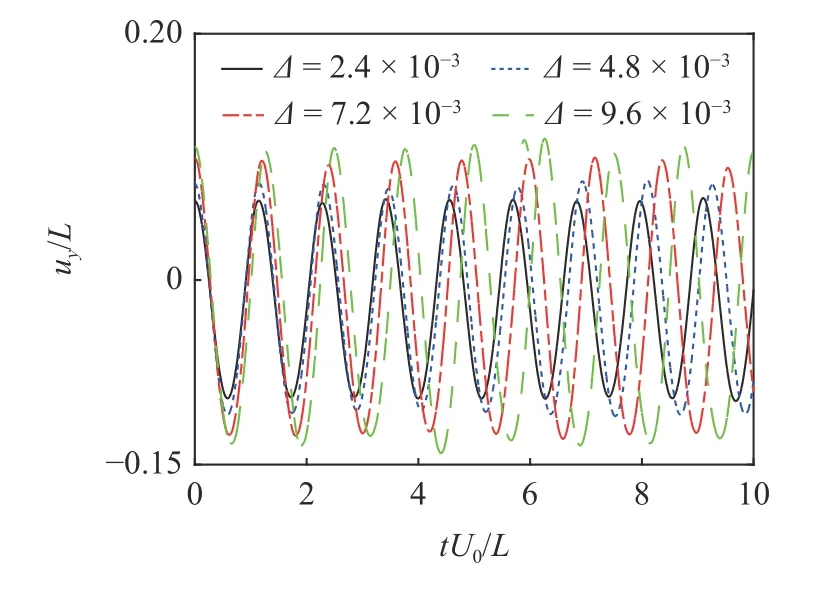
图16 层合梁右端(x=L)节点的横向位移时域响应Fig.16 Time domain response of transverse displacement at beam tip

进一步对比上下两层弹性模量的差异对振动响应运动轨迹的影响.不同刚度比情况下,20 个振动周期内,层合梁右端节点位移的Lissajous 曲线如图17 所示,红色虚线表示横向位移的平均值.当刚度比较小时,Lissajous 曲线上下对称,运动轨迹是‘8’字形;当刚度比 ∆ 较大时可以发现Lissajous 曲线不对称的现象,层合梁向下振动的弯曲程度大于向上振动的弯曲程度.

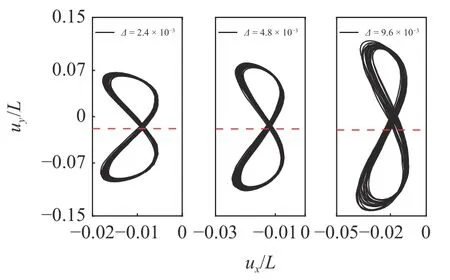
图17 层合梁右端(x=L)节点位移的Lissajous 曲线Fig.17 Lissajous curves of displacements at beam tip

3.4 厚度占比对剪切流中层合梁振动的影响

本节研究剪切流中层合梁上下两层的不同厚度占比对振动特性的影响,定义上铺层厚度占比 γ=Ht/(Hb+Ht).考虑剪切速度分布 α=1,分析了刚度比 ∆=0.0048 和 ∆=0.0096 两种情况下,上铺层厚度 γ ∈[0,1] 的层合梁振动特性,其他无量纲参数与3.2 节相同.

图18 和图19 分别给出了两种刚度比情况下,10 个振动周期内,层合梁右端节点横向位移标准差和平均值曲线随厚度占比 γ 变化的曲线.图18 表明,在γ <0.8 的区间内,随着厚度比的增加,层合梁的振动幅度逐渐降低;在0.8 <γ <0.9 的区间内,层合梁的振动从大幅度周期极限环振动模式(P)转变到静变形为主的定点稳定模式(S),两种模式下的变形包络图在图18 中给出.图19 表明,随着刚度较大的上铺层厚度占比的增加,剪切流作用下层合梁的平均偏斜量减少.结合图18 和图19 中的结果分析,厚度占比 γ=0 和 γ=0.1 时,刚度比差异大(∆ ＝ 0.0096)的层合梁平均偏移量更大,但振幅更小;在0.2 <γ <0.8 的区间内,刚度比差异大(∆ ＝ 0.0096)的层合梁平均偏移量和振幅均大于刚度比差异小的层合梁;当 γ >0.8 时,层合梁处于定点稳定变形模式,刚度比大的层合梁的平均偏斜量小.

图18 层合梁右端(x=L)节点的横向位移标准差曲线以及 γ=0.33,γ=1 时的变形包络图Fig.18 Standard deviation of transverse displacement at beam tip as a function of γ and deformation envelope of beam at γ=0.33,γ=1,respectively

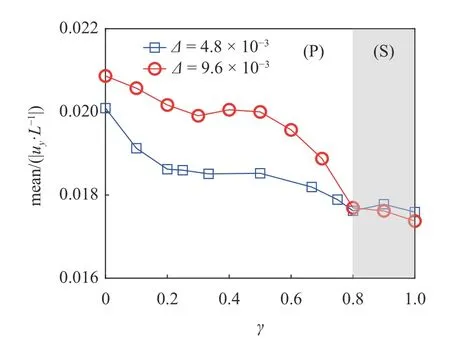
图19 层合梁右端(x=L)节点的横向位移平均值曲线Fig.19 Mean value of transverse displacement at beam tip as a function of γ

结果表明,层合材料对复合材料梁的动力学行为有显著影响,相同的流场条件下层合特性的轻微改变会导致动力学行为的突变,这可以归因于厚度比的变化影响了层合梁的等效刚度,进而影响了剪切流−层合梁系统的稳定性.

3.5 铺层角度对剪切流中层合梁振动的影响

本节研究剪切流中层合梁上下两层厚度相同,材料相同,不同的铺层角度对振动特性的影响,采用与3.2 节相同的无量纲参数,各向异性复合材料参数如下:E2=E1/10,G23=G13=G12=E1/20 .定义铺层角度 θ,层合梁的铺层方式表示为 [ θ,−θ] .考虑剪切速度分布 α=1,分析了铺层夹角 θ ∈[0◦,90◦] 的复合材料层合梁振动特性.

图20 给出了20 个振动时长内层合梁右端节点横向位移标准差值曲线随铺层角度 θ 变化的曲线,其中蓝色散点表示不同角度 θ 情况下20 个振动时长内的位移曲线幅值极大值.结果表明,随着铺层角度的增加,层合梁的振动模式从周期极限环振动模式(P)转变到非周期振动模式(NP).非周期振动模式在大多数情况下无法识别极限环,通常是概周期或混沌运动,在这种非周期状态下,由于运动的随机性导致了位移曲线的幅值极大值具有不稳定性;另一方面,位移的标准差曲线保持了连续性,非周期振动模式与周期极限环振动模式下的标准差具有相同的数量级.图21 给出了20 个振动时长内,层合梁右端节点横向位移平均值曲线随铺层角度 θ 变化的曲线,θ=35°和 θ=40°情况下右端节点的Lissajous 曲线也在图21 中给出.随着铺层角度的增加,层合梁的等效刚度减少,导致剪切流作用下层合梁的平均偏斜量增大.

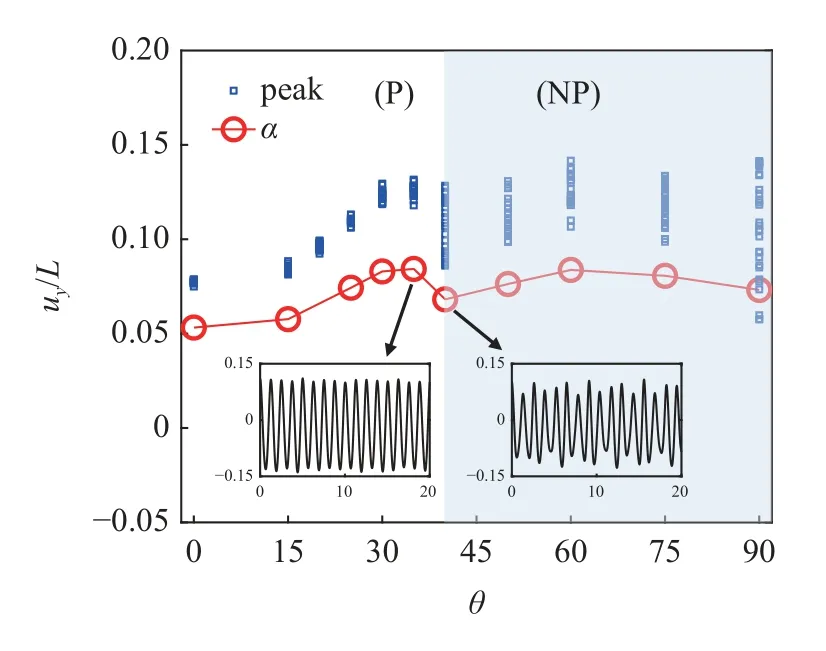
图20 层合梁右端(x=L)节点的横向位移标准差曲线以及 θ=35°,θ=40°时的时域曲线Fig.20 Standard deviation of transverse displacement at beam tip as a function of θ and time domain response at θ=35°,θ=40°,respectively

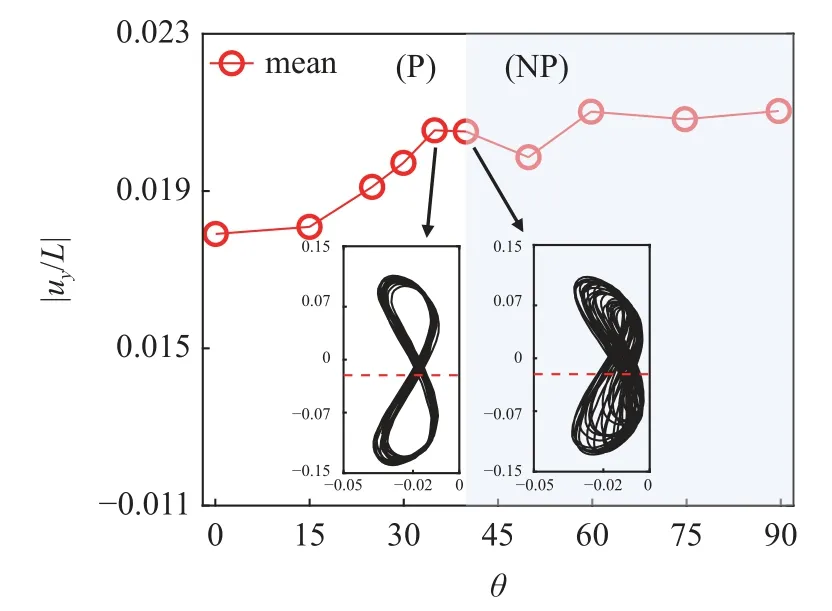
图21 层合梁右端(x=L)节点的横向位移平均值曲线以及 θ=35°,θ=40°时的Lissajous 曲线Fig.21 Mean value of transverse displacement at beam tip as a function of θ and Lissajous curves at θ=35°,θ=40°,respectively

4 结论

本文对剪切流作用下复合材料层合梁的振动特性进行数值建模和计算,得到了以下结论.

(1)剪切流作用下单层梁的振动特性与均匀流作用下不同,梁的振动受剪切流影响向下偏斜,随着速度分布系数增加,单层梁振动的不对称性逐渐明显,振动的幅度和主导频率(涡脱落频率)均是先减小后增加,尾部流场中的涡结构发生改变.

(2)刚度比对剪切流作用下层合梁的振动特性有显著影响.随着刚度比的增加,层合梁振动的振幅增大,主导频率下降,运动轨迹由“8”字形逐渐变得不对称,层合梁向下振动的弯曲程度大于向上振动的弯曲程度.

(3)厚度占比对剪切流作用下层合梁的振动特性有显著影响.随着厚度占比的增加,观察到两种不同的响应状态:大幅度周期极限环振动模式(P)转变到静变形为主的定点稳定模式(S).

(4)复合材料铺层角度对剪切流作用下层合梁的振动特性有显著影响.随着铺层角度的增加,观察到振动模式由周期极限环振动模式(P)向非周期振动模式(NP)转变.