深海采矿系统中悬臂式立管涡激振动分析1)

金国庆 邹 丽 ,†,2) 宗 智 ,† 孙 哲 王 浩

* (大连理工大学船舶工程学院,工业装备结构分析国家重点实验室,辽宁大连 116024)

† (高技术船舶与深海开发装备协同创新中心,上海 200240)

** (中国水利水电科学研究院,北京 100038)

引言

海底蕴藏着丰富的矿产资源,目前已知的包括多金属结核物、多金属硫化物、富钴结壳和深海稀土资源等,具有重要战略意义与商业开采价值[1-2].这类矿产资源大多富含于数千米水深的深远海底部,赋存状态的特殊性和周围环境的复杂性导致开采难度较大[3-4].目前主流的深海采矿方式为垂直管道混输系统,即采用水力提升的方式将矿物通过长距离的管道输送至水面采矿船.该系统主要由海底采矿系统、垂直输运系统和水面支持系统三部分组成[3].如图1 所示,海底采矿车收集矿物并通过软管输送到中间仓(缓冲仓),之后利用水力提升泵将矿物通过垂直提升管道输送至水面母船[5-9].

图1 深海采矿系统示意图Fig.1 Sketch of the deep-sea mining system

矿产混输系统中的关键装备之一为具有大长细比特征的垂直提升管道.不同于传统的海洋立管,垂直提升管道底部与中间仓相连接,其底部是自由运动的状态,因此该输运管道通常被称为悬臂式或自由悬挂式立管.类似的立管形式在油气资源开采系统中也会遇到,当遭遇极端海况或者回收输油管道时,输油管道底部脱离井口,呈现自由悬挂式状态[10-12].在深海采矿垂直提升管道的研究中,底部中间仓重量可简化为一个垂直向下的作用力,立管底部可视为弱约束状态.然而,目前对此类立管的研究主要集中在结构动力学行为分析[11-15],缺乏对其水动力学性能的研究.

与传统立管类似的是,悬臂式立管在作业过程中也面临着涡激振动(VIV)等水动力学问题.涡激振动指的是流体经过钝体结构物,从物体表面分离后在尾部交替地产生旋涡,进而产生周期性的外力和振动.在一个质量-弹簧-阻尼系统中,当振动频率和泻涡频率一致时,出现锁定共振现象,此时结构物会产生大幅度的振动,严重危害作业安全.此外,长期的立管振动会导致结构出现疲劳损伤.因此,立管的涡激振动研究是立管水动力性能分析的重要组成部分.对于立管的涡激振动特性的测量,传统的做法是采用缩尺模型进行水池试验.Chaplin 等[16]针对一根长13.12 m 的柔性立管,进行了阶梯流作用下的VIV 试验研究,观察到了立管在一定流速下被激发出高阶模态振动.Trim 等[17]开展了水平布置的38 m 长的立管分别在均匀流和剪切流作用下的试验,分析了不同拖曳速度下的振动模态和频率等特征.Song 等[18-19]和高云等[20]研究了7.9 m 长立管在不同流速的均匀流作用下的非均匀分布的水动力载荷、立管截面运动轨迹和疲劳损伤等问题.此外,王俊高等[21]研究了正弦振荡来流下小尺度模型立管的VIV 特性.徐万海等[22]则结合拖曳水池试验和数值模型分析了立管的流体力系数特性.在悬臂式立管模型试验方面,文献[10]研究了水面母船运动对立管动力行为的影响.Fujarra 等[23]研究了悬臂式管道在一阶振动模态下的锁定问题.Wang 等[24]分析了船舶周期性运动对自由悬挂式立管运动响应的影响.Mao 等[25]测量了悬挂式排空采油管道在不同流速下的振动模态和振幅.然而,模型试验成本高且周期较长,此外,缩尺模型需要改变立管的材料属性,产生难以避免的误差.

近年来,数值手段成为研究立管涡激振动的主要方式.常见的立管振动预报数值方法主要分为三类:经验模型、参数化模型和CFD 模型[26].其中,经验模型常采用尾流振子模型获得作用在结构上的流体力,进一步通过梁模型求解立管变形[27-29].参数化模型则是基于一系列的刚性圆柱涡激振动试验结果来确定立管运动幅值[30],该方法已形成相关的计算软件,例如Shear 7 和VIVANA 等.可以看出,前两者分别属于经验和半经验方式,因此其计算成本相对较低.计算流体力学方法则是通过求解Navier-Stokes (N-S)方程,获得立管尾流场的非定常流动特征和时域内变化的水动力载荷.常见的方法是基于切片法的思想,采用CFD 模型求解立管若干节点的受力,通过有限元方法求解柔性立管变形和振动[31-34],这类准三维的数值模拟手段可兼顾计算效率和精度.此外,部分研究采用高精度的大涡模拟LES 方法[35]和直接数值模拟DNS 方法研究低雷诺数下柔性立管的涡激振动[36-37],但该方法目前所需计算资源较大,难以求解高雷诺数下大长细比立管的水动力问题.

综上所述,基于CFD 模型和有限元的耦合求解算法,可有效求解具有大长细比特征的海洋立管的涡激振动问题.其中,离散涡方法(DVM)[38]作为一种无网格的纯拉格朗日的流体计算方法,可以高效率地求解高雷诺数下的圆柱绕流问题,通过与有限元方法(FEM)结合,近年来被发展用于研究立管的VIV 问题[31-32,39-40].此外,目前海洋立管研究主要集中于传统的两端铰支的立管形式,缺乏对深海采矿系统中采用的悬臂式立管水动力性能的研究.本文基于准三维的DVM-FEM 耦合算法,建立悬臂式立管涡激振动的计算模型,即立管上端固定,底部无约束且承受一定的向下的拉力.主要目的是系统性地研究不同流速下悬臂式立管的振动响应,分析其振动模态、频率和振幅等主要特征.本文首先分别介绍了二维离散涡算法和有限元模型.其次,通过数值预报与经典的9.63 m 长立管在均匀流作用下的试验结果[41]的对比,验证了本文采用的耦合算法可以较好地预报柔性立管的振动响应.最后,研究不同折合速度下悬臂式立管的VIV 特征,分析其与两端铰支立管的异同.本工作可为深海采矿混输提升系统的设计和振动行为分析提供参考.

1 DVM-FEM 耦合算法

本文所采用的耦合算法基于切片法的思想,将立管沿垂向划分成若干切片,在每个切片上通过二维离散涡算法求解弹性圆柱涡激振动问题,并获得该切片所对应的节点的水动力载荷.此外,基于有限元方法建立柔性立管振动求解的控制方程,通过迭代求解获得立管振动的时域解.综上,该耦合算法主要包括流体求解器和结构求解器两部分,所对应的算法分别为离散涡和有限元方法.

1.1 流体求解器:离散涡方法

离散涡算法是一种纯拉格朗日粒子算法,不需要进行复杂的网格划分,涡元在物面上生成,运动后的涡元主要集中在边界层和尾流区域,因此具有较低的计算成本[38,42].根据质量守恒和动量守恒定律,离散涡算法的控制方程为连续性方程和N-S 方程,即

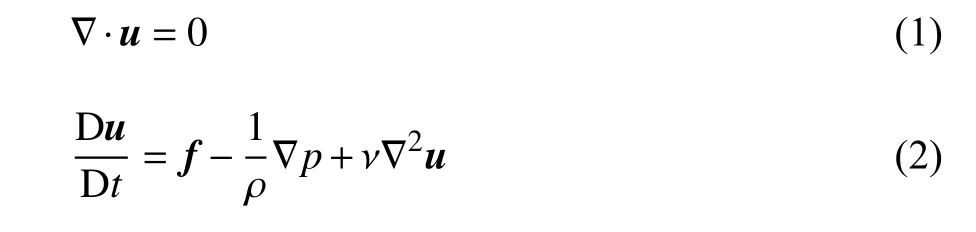
式中,u为速度矢量,D/Dt为物质导数,f为质量力,ρ 为流体密度,ν 为运动黏度.对式(2)两侧取旋度,可得到二维涡量输运方程

式中,ω 是垂直于二维水平面方向上的涡量分量

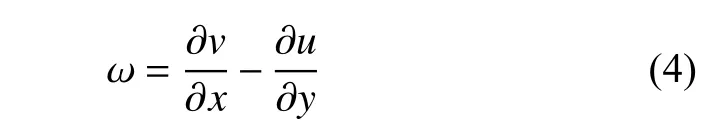
式中,u和v分别是速度在x和y方向上的分量.离散涡方法引入流函数 ψ,速度分量可表示为

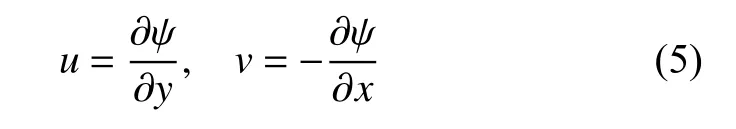
将方程(5)代入式(4)中可得Poisson 方程

Chorin[38]采用算子分裂法的思想,将涡量输运方程分解为两部分求解,分别为对流和扩散方程

对流项

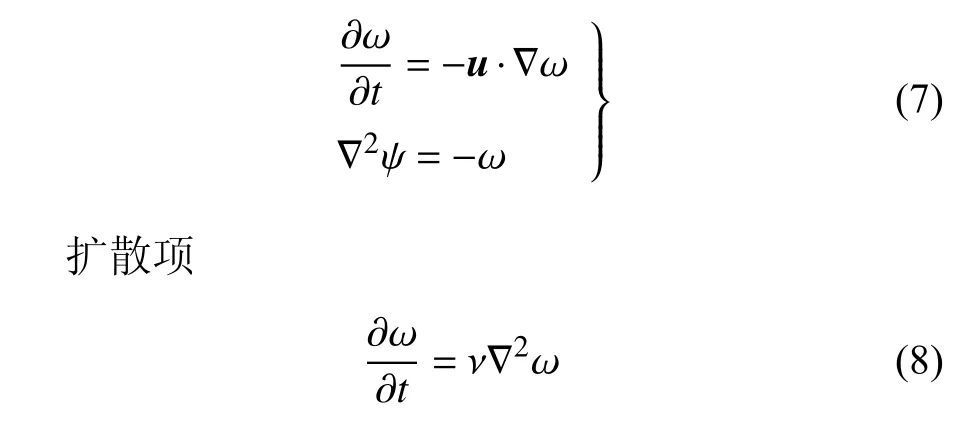
通过Biot-Savart 定律可求解对流项方程,涡元对流速度由涡元之间的诱导速度和来流速度两部分组成,基于Spalart 等[42]提出的涡核模型,数值计算过程中的对流速度可表示为

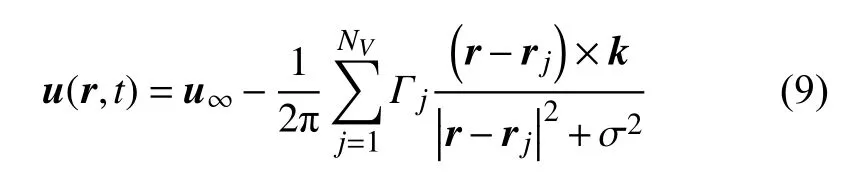
式中,u∞=(u∞,0) 为来流速度,r=(x,y) 为涡元位置坐标,Γ 为涡元强度,σ 为涡元半径,k为二维平面垂向单位矢量.对于扩散项,基于Chorin[38]提出的随机扩散法求解扩散方程,即

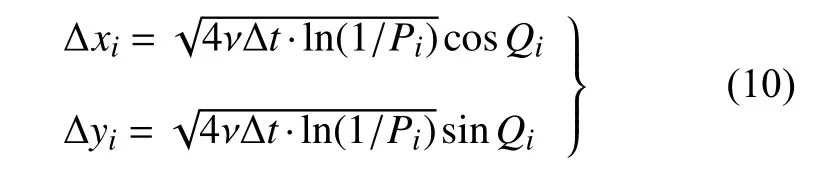
式中,∆xi和 ∆yi分别为第i个涡元在两个方向的随机步长,∆t为迭代时间步,Pi和Q分别为介于 (0,1) 和(0,2π)的随机数.采用二阶Runge-Kutta 法进行时间积分,涡元i在t+∆t时刻的新位置为

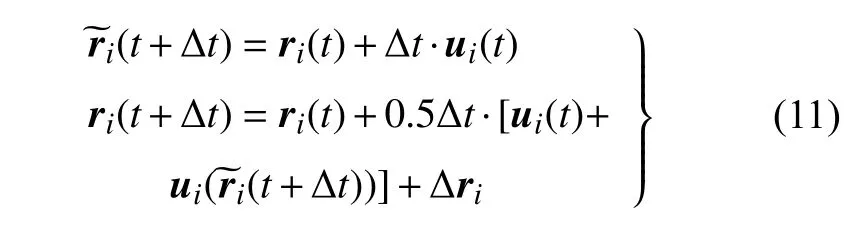
求解物面压力分布时,由于物体是运动的,因此需在压力求解中考虑加速度项,即

式中,p为物面压力,s表示物面切向,ab为物体运动加速度.

离散涡算法具体的实现过程可参考文献[43-44].需要注意的是,涡元在运动过程中会进入物体内部,本文采用瞬态涡量守恒方法,将进入圆柱内部的涡元基于圆周定理映射到物体外部,保证单个时间步内流场涡量是守恒的,具体实现步骤可参考文献[44-45].

1.2 结构求解器:有限元方法

海洋柔性立管具有大长细比的特征,可简化为一根垂直的Euler-Bernoulli 梁模型.通过Galerkin 方法,可获得立管结构动力响应计算的有限元控制方程[31-32],即

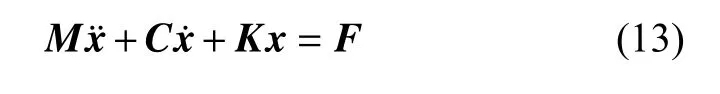
式中,M,C,K分别为质量、阻尼和刚度阵,F为外力矢量,x为立管各节点组成的位移矢量.其中外力矢量由离散涡算法提供,阻尼采用Rayleigh 阻尼模型,即

式中,α 和 β 为瑞利阻尼系数,计算方式为

式中,ξ 为阻尼比,ω1和 ω2分别为立管的前两阶固有角频率,可通过模态分析获得,本次计算模态分析采用子空间迭代法[46].

需要注意的是,传统的两侧铰支立管高度为 2 处的张力T(z) 由顶部张力、包含管内流体重量的立管结构自重和浮力项三部分组成,即

式中,Ttop为顶部张力,ztop为立管顶端高度,ws和wb分别为单位长度立管的自重和所受到的浮力.对于底部有附加重量的悬臂式立管,其所受张力由参考文献[25-47]给出

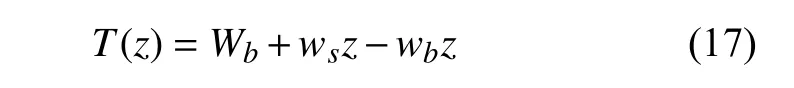
式中,Wb为立管底部承受的向下的拉力,即深海采矿系统中中间仓的重量.

如图2 所示,悬臂式立管可简化为一个柔性悬臂式模型,其底部连接的中间仓可简化为一个垂直向下的力Wb,需要注意的是该力学模型忽略了中间仓惯性力的影响.未来工作中可以将中间仓简化为一个集中质量节点进行结构动力响应分析,并且可以研究这两种力学模型的异同.

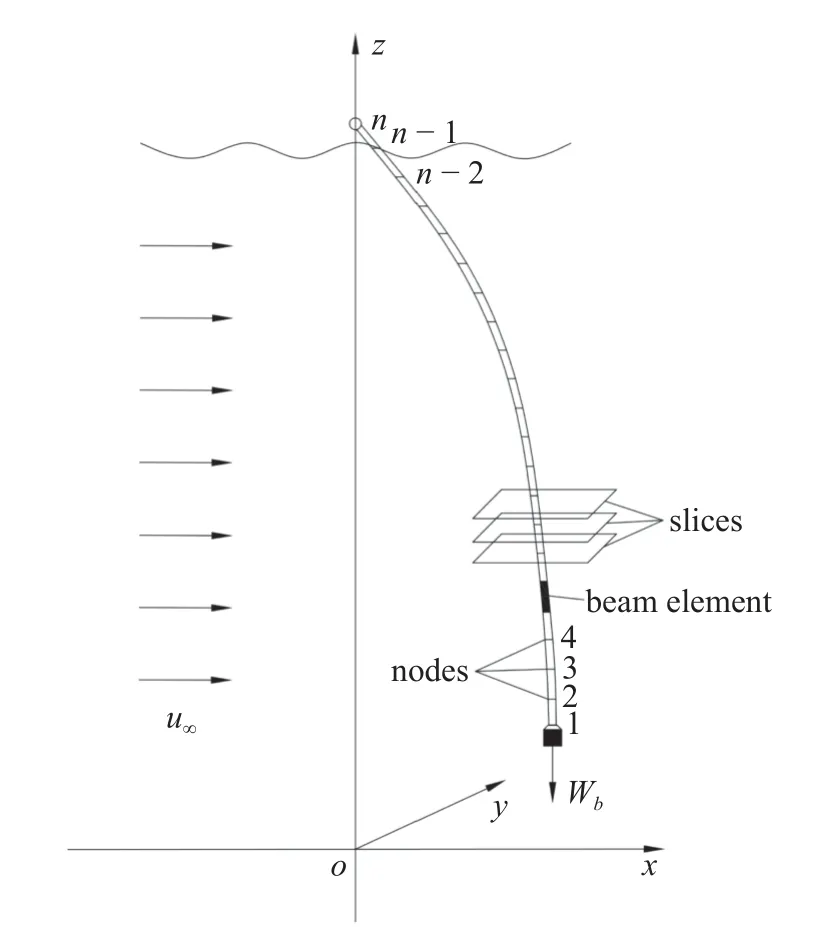
图2 垂直提升管道简化模型Fig.2 Simplified model of the vertical lifting pipeline

综上所示,基于切片法的思想,立管被划分成一系列的梁单元,基于离散涡方法求解立管各单元节点所受的外力,采用有限元方程求解柔性立管结构变形,本文采用Newmark 方法[46]迭代求解每个时间步内的立管振动位移、速度和加速度,采用弱耦合的形式实现流体和结构求解器之间的数据交换.在接下来的内容中,本文首先通过与经典的立管模型对比来验证该耦合算法的有效性,进一步分析悬臂式立管的VIV 特性.

2 数值模型验证

由于悬臂式立管的模型试验基准算例较少,在这一节中仍采用顶端和底部均为固定边界条件的模型试验进行数值验证.基于DVM-FEM 耦合算法的计算程序由本文作者自主开发,采用Fortran 语言编写.如表1 所示,物理模型试验[41]中的立管总长度为9.63 m,立管外部直径为20 mm,厚度为0.45 mm,顶部张力为817 N,分别计算均匀流速0.42 m/s 和0.84 m/s 两个流速下的立管振动响应.

表1 柔性立管参数[32,41]Table 1 Parameters of a flexible riser[32,41]

本文的耦合算法基于切片法,切片数量对计算成本有重要影响,选取合适的立管单元数N可在保证计算精度的基础上提高求解效率.本次研究选择了4 套立管单元数进行敏感性分析,数量分别为30,60,90 和120.在0.42 m/s 来流速度作用下,不同单元数计算得到的立管横向振动位移均方根值如图3 所示.可以看出,立管单元数量变化对其振幅和模态的影响均较小,选取N=60 时即可满足立管单元数量收敛性要求,因此本文所有模拟采用的立管单元数均为60.

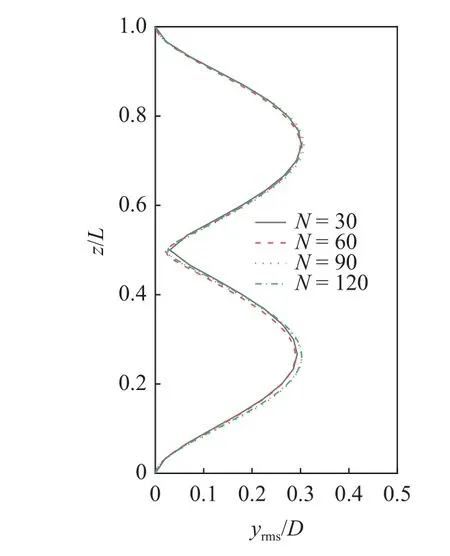
图3 不同单元数立管的横向位移均方根值Fig.3 RMS amplitudes of the transverse displacements for the riser models with various element numbers

两个来流速度下的立管在不同时刻的横向振动位移包络线和对应的均方根值如图4 所示.可以看出,在0.42 m/s 流速下,立管横向呈现出2 阶振动模态.高流速下激发出了更高阶的振动模态,在0.84 m/s 流速作用下,立管横向振动呈现出4 阶模态.进一步对比横向振动位移的均方根值,如图4(b)和4(d)所示,图中同时给出了文献[32,48-49]的数值模拟结果.结果表明:数值预报的振动模态阶数与试验和其他数值模拟结果均是一致的,但振动幅值相比试验结果是偏小的,目前算法在准确预报柔性立管振动幅值方面仍有待改进.本文数值模型预报立管振幅偏小的原因可能是多方面的,首先,DVMFEM 耦合算法基于切片法的思想,将立管简化为梁模型进行结构动力响应求解,忽略了立管本身三维效应的影响以及尾流中三维涡结构的影响,Huang等[48]和Wang 和Xiao[49]则是采用完全三维网格的方法求解流场和立管变形;其次,Wu 等[50]的研究表明立管流向和横向运动之间存在相互作用,本文采用的耦合算法则是单独求解每个方向的立管结构动力响应;此外,离散涡方法本身及其与有限元方法的耦合方式仍有待进一步的研究与改进.

图4 不同流速下的柔性立管横向振动响应((a),(c)振动位移包络线;(b),(d)位移均方根值)Fig.4 Vibration response envelopes of a flexible riser under different current speeds ((a),(c) vibration amplitude envelopes;(b),(d) RMS displacements)

3 悬臂式立管计算结果与分析

本节主要关注不同流速下的悬臂式立管的涡激振动响应特征,同样选用上述9.63 m 长的立管,其底部承受的向下的拉力设定为Wb=817 N,这与原来两端铰支的立管试验中所选择的顶部张力在数值上是相同的,其他物理参数保持不变.因此,不同流速作用下的柔性立管的固有频率是一致的.基于子空间迭代法可获得立管湿模态下的前8 阶固有频率及其对应的归一化的振型,如图5 所示.立管的固有频率随模态阶数的增加而增大,本文以1 阶固有频率f1=0.78 Hz 为参考值,取折合速度Ur从4 到46,间隔为2,计算得到的实际流速区间为u∞=0.0626～0.6884,对应的雷诺数区间为Re=1252～ 13768.折合速度计算公式为

图5 悬臂式立管前8 阶固有频率和振型Fig.5 First eight-order natural frequencies and modal shapes for a cantilever riser

雷诺数计算公式为

基于结构物绕流的升力时历曲线,采用快速傅里叶变换(FFT),可得到泄涡频率fs,进一步可计算斯特劳哈尔数

3.1 振动响应分析

首先,本文计算了不同折合速度下的柔性悬臂式立管的横向振动,振幅均方根值随Ur和z/L的变化情况如图6 所示.可以看出,随着折合速度的增加,立管振动模态逐渐增加,在较高折合速度下高阶模态被激发.在Ur=4～ 46 范围内,横向振动逐渐由1 阶模态向4 阶模态过渡.立管振幅则呈现出波浪式的变化特征,即在一定的折合速度范围内,立管的振动模态是相同的,这与Fan 等[35]对两端铰支柔性立管VIV 的研究结果类似.当立管呈现出相同模态时,随着Ur的增加,立管振幅逐渐增加,同时在少数折合速度下振幅没有呈现出线性增长的特征.当振动从低阶模态向高阶模态转变时,模态阶数的跃迁过程中会伴随着振幅的突然降低.此外,可以很明显地观察到无约束的立管底部表现出较大幅度的位移.

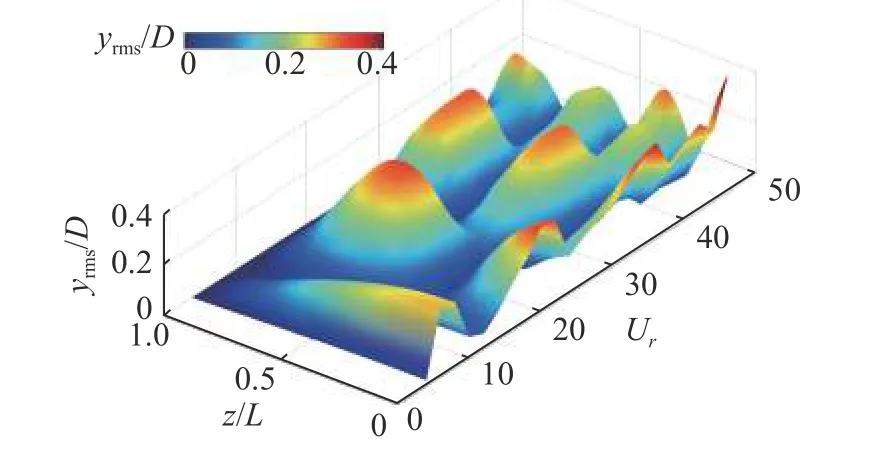
图6 不同折合速度下的横向振幅均方根值Fig.6 RMS vibration amplitudes in the transverse direction under a wide range of reduced velocities

针对不同振动模态下立管的变形特征,本文分别将1 阶到4 阶模态下立管横向振动的位移均方根值进行了比较分析,如图7(a)到图7(d)所示.并且列举了四种振动模态下某一折合速度对应的立管瞬态振动包络线图,如图7(e)到图7(h)所示.同样可以看出,大部分情况下,沿立管展向各位置处的横向位移随折合速度增加而逐渐增大,该变化特征在3 阶模态情况下最为明显,如图7(c)所示.此外,在同一振动模态下,振幅最小处所对应的立管展向位置基本上是相同的,与来流速度关系较小.

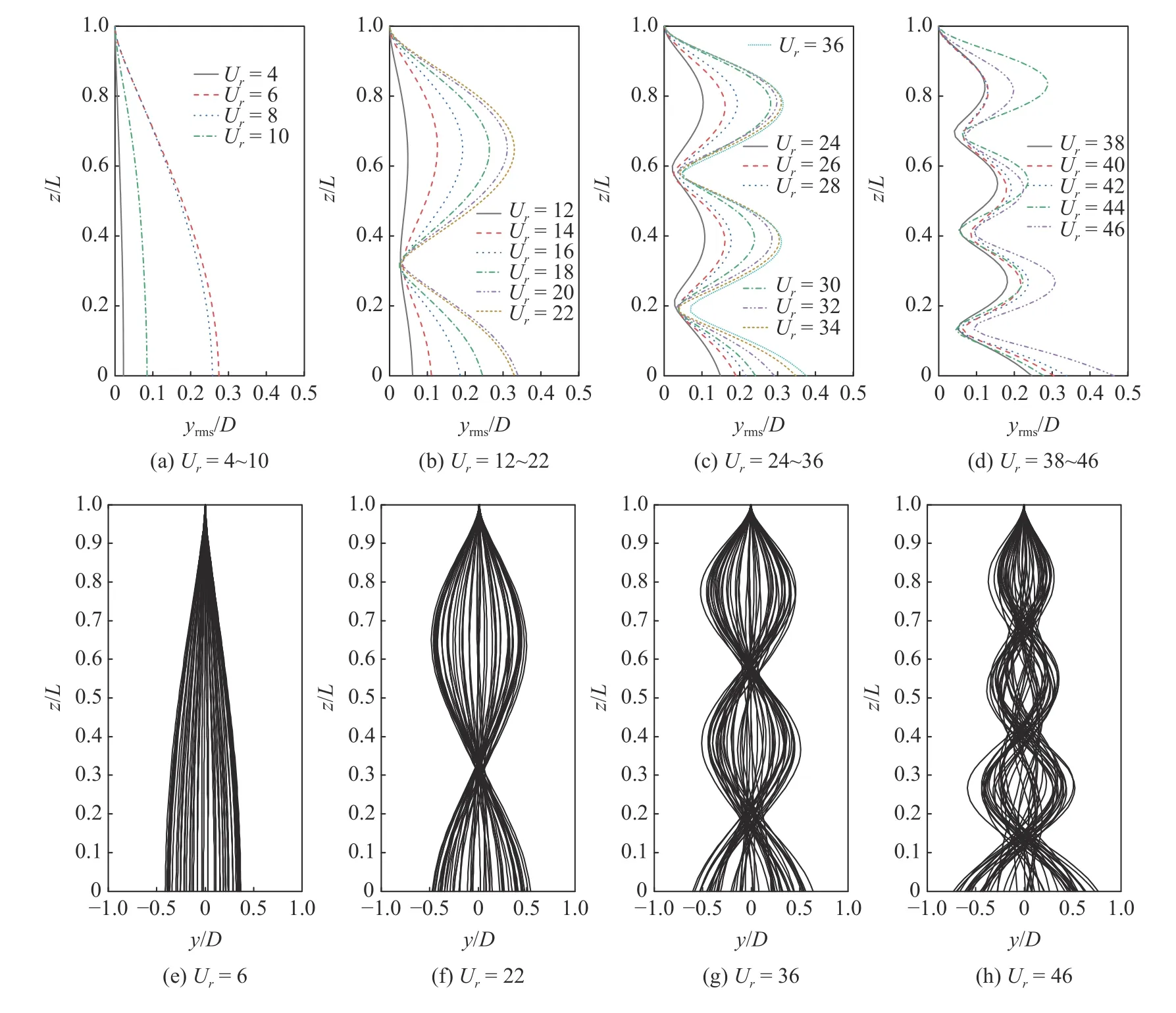
图7 不同折合速度下的柔性立管横向振动响应 ((a)～(d)位移均方根值;(e)～(h)振动位移包络线)Fig.7 Vibration response envelopes of a flexible riser under different reduced velocities ((a)～(d) RMS amplitudes;(e)～(h) vibration amplitude envelopes)

在深海采矿系统中,悬臂式立管底部与中间仓相连接,矿物经输料软管到达中间仓,再通过垂直提升硬管输送到水面母船.因此,立管底部的振动对矿物输运的稳定性有较大的影响.本文将中间仓简化为有一个作用在立管底部的垂直向下的作用力进行研究,如图2 所示.由上述分析可知,悬臂式立管底部位置有较大幅度的位移,不同折合速度下的立管底部位移均方根值如图8 所示.可以看出,不同模态下振幅的增长速率是不同的.在同一振动模态下,立管底部振幅与折合速度基本上呈现出线性关系.

图8 立管底部横向位移均方根值Fig.8 RMS amplitude of the transverse displacement at the bottom for the riser

不同折合速度下立管振动的主导频率fv如图9 所示.图中St=0.2 这条线表示当圆柱在亚临界雷诺数范围内振动时,其对应的斯特劳哈尔数位于0.2 附近[51].整体上,振动频率随着折合速度的增加而逐渐增大.当振动模态发生转换时,振动频率会发生突然的跳跃.在同一振动模态内,振动主导频率在低折合速度下沿着St=0.2 增加,且频率值低于所对应振动模态下的固有频率.随着折合速度进一步增加,当振动频率超过固有频率后,主导频率逐渐偏离S t=0.2 所对应的频率值,该现象与刚性圆柱涡激振动是类似的[52].

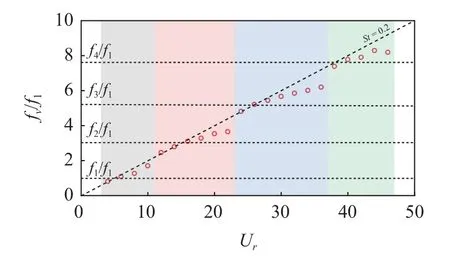
图9 横向振动的主导频率比Fig.9 Dominant frequency ratio of the transverse vibration

3.2 三阶模态下横向振动响应分析

由上文分析可知,悬臂式立管发生涡激振动时,其振动模态在一定折合速度范围内是相同的,因此本节选取典型的3 阶振动模态进行讨论.本文中立管以3 阶模态振动时所对应的折合速度Ur=24～36,间隔为2,共7 个工况,所对应的横向振幅均方根值如图7(c)所示.基于立管垂向不同位置振动时历曲线,采用快速傅里叶变换(FFT)方法对时历数据进行频谱分析,可得到振动频率的空间分布特征,如图10 所示.其中颜色条为归一化的振动能量谱密度(PSD),白虚线表示3 阶振型所对应的固有频率,f3=4.07 Hz.可以看出,7 种折合速度对应的振动频率均由3 阶模态主导,且不同折合速度下立管底部均呈现出较高能量的振动.此外,随着折合速度增加,振动频率逐渐远离3 阶固有频率.

同样采用FFT 方法,可得到不同折合速度下的立管展向各位置处的泄涡频率空间分布,如图11 所示,其中白虚线均表示St=0.2 所对应的频率值.与图10 相比,不同折合速度下泄涡频率与振动频率基本上是一致的.在低折合速度下,立管各位置处的泄涡频率均集中在St=0.2 附近,随着速度增加,立管展向大部分位置所对应的泄涡频率逐渐低于S t=0.2所对应的频率值,尽管仍有较少位置的泄涡频率集中在St=0.2 附近.不同折合速度下的泄涡频率在立管展长方向上并未呈现出明显的分布特征,这与振动频率空间分布图中呈现出的3 阶分布特征是不同的.

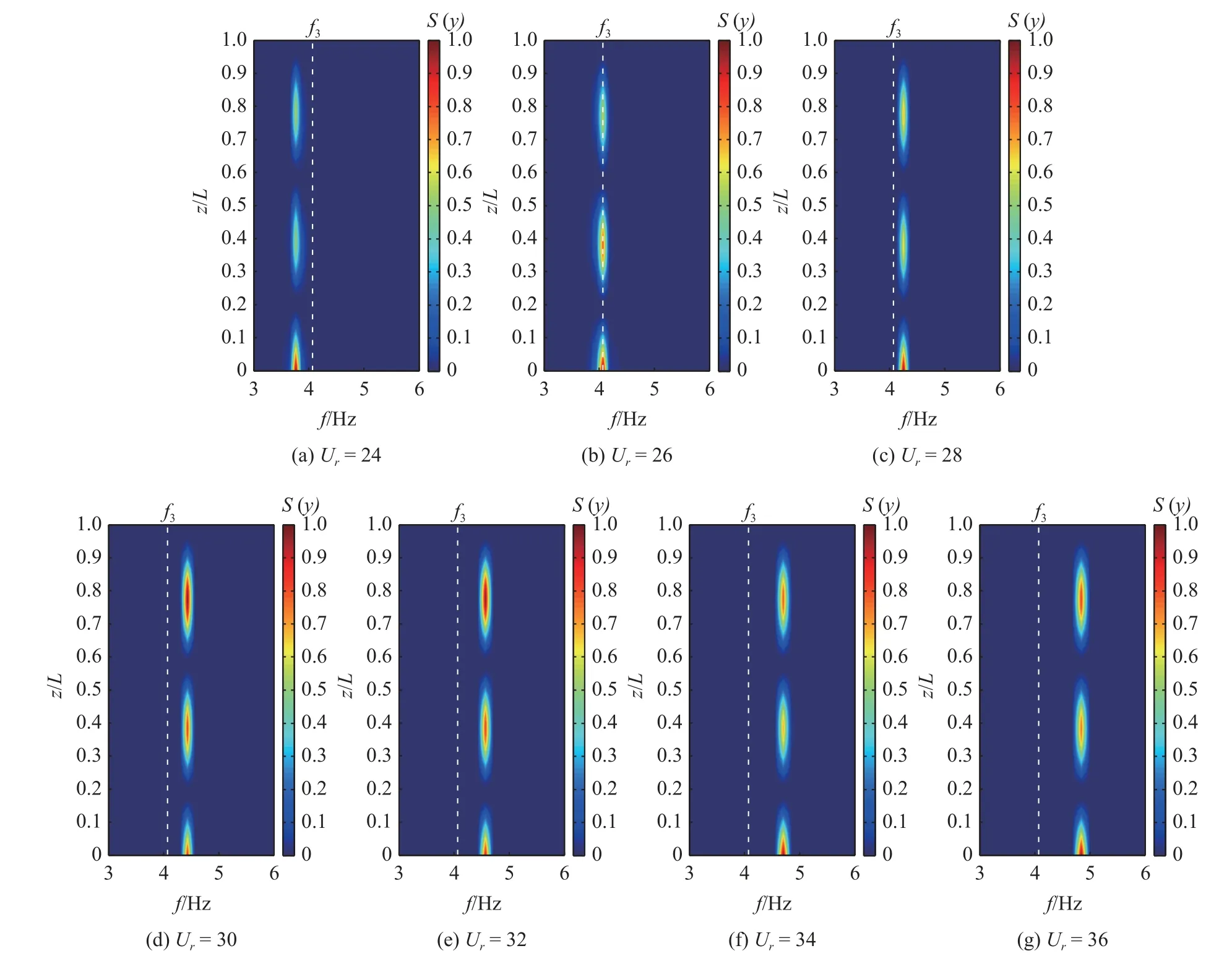
图10 立管横向振动频率空间分布 ((a)～(g) Ur=24～36)Fig.10 Spatial distribution of transverse vibration frequency for the riser ((a)～(g) Ur=24～36)

图11 立管泄涡频率空间分布 ((a)～(g) Ur=24～36)Fig.11 Spatial distribution of vortex shedding frequency for the riser ((a)～(g) Ur=24～36)

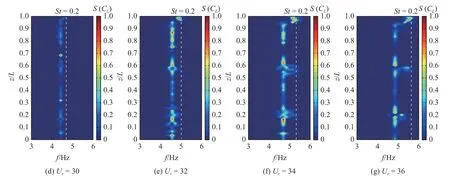
图11 立管泄涡频率空间分布 ((a)～(g) Ur=24～36) (续)Fig.11 Spatial distribution of vortex shedding frequency for the riser ((a)～(g) Ur=24～36) (continued)

3 阶振动模态下不同折合速度所对应的立管横向振幅时空演化特征如图12 所示,所有时空演化图选择的时间段均为6～8 s,其中红色和蓝色表示相反的振动方向.可以看出,随着折合速度的增加,立管展向不同位置处的振幅增加,且在该时间段内驻波特征逐渐增强.由上文分析可知,同一振动模态下,振动频率随折合速度的增加而增大,因此相同时间段内红蓝单元交替的周期逐渐减小.

图12 立管不同位置的振幅时空演化 ((a)～(g) Ur=24～36)Fig.12 Temporal-spatial evolution of transverse vibration amplitude along the riser span ((a)～(g) Ur=24～36)

本文工作基于切片法的思想,在切片上采用无网格的二维离散涡算法计算流体力,四种折合速度下(Ur=24,28,32,36)的立管若干截面处的瞬态涡量场如图13 所示.可以看出,随着折合速度的增加,立管底部的流向位移逐渐增大.立管不同高度截面涡量场中红色和蓝色粒子分别表示涡元具有正向和负向的涡量.立管不同截面处的尾流场中的涡结构具有不同的模式[53],其中大部分截面呈现出2 S 的尾涡模式.此外,近尾流场涡结构比较清晰,而远尾流场则演化出更为复杂的涡结构特征.

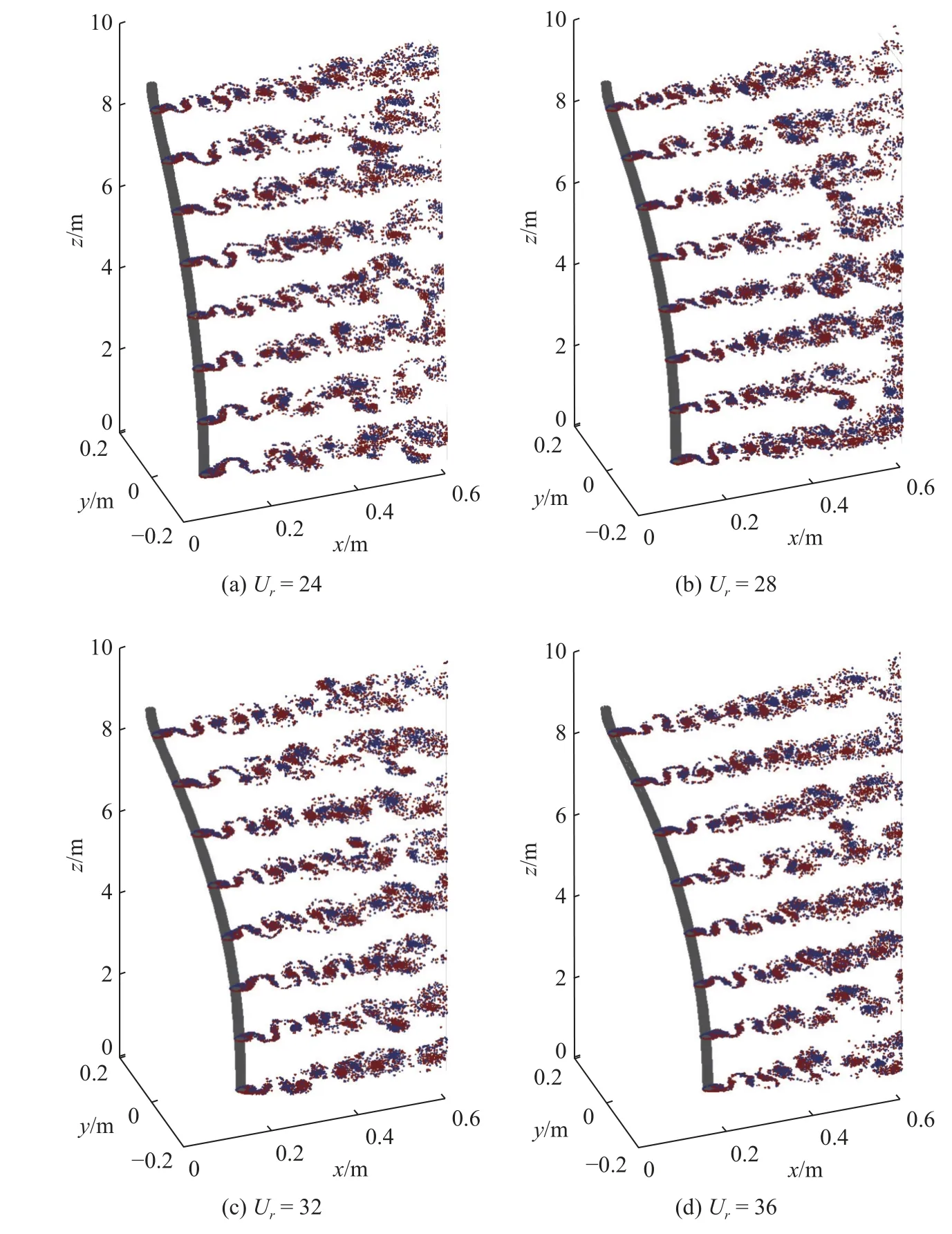
图13 瞬态涡量场 ((a)～(d) Ur=24～30)Fig.13 Instantaneous vorticity field ((a)～(d) Ur=24～36)

3.3 两端铰支与悬臂式立管的涡激振动特征比较

为了比较传统的两端铰支立管(对应海洋工程中的采油管道)与悬臂式立管(对应深海采矿的提升管道)涡激振动特征的异同,本文计算了一系列均匀流速作用下的两端铰支的9.63 m 长立管的涡激振动响应.立管顶部张力与试验保持一致,取为Ttop=817 N.立管湿模态下的前8 阶固有频率及其对应的归一化的振型,如图14 所示.可以看出,两端铰支立管的各阶固有频率均大于对应的底部拉力为817 N 的悬臂式立管的固有频率.两端铰支立管的1 阶固有频率f1=1.61 Hz,本次计算取折合速度Ur=4～ 44,间隔为2.计算得到的不同来流速度作用下立管最大的横向位移均方根值如图15 所示,图中不同颜色块表示不同的振动模态.可以发现,横向振幅的变化规律与悬臂式立管是一致的,即在同一振动模态下,立管振幅与折合速度基本上呈现出线性关系.此外,当模态转变发生时,振幅会突然降低,并随着折合速度增加,振幅再一次逐渐增大,这与悬臂式立管的VIV 特征也是相同的.

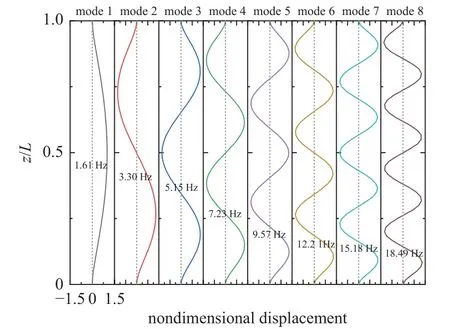
图14 两端铰支立管前8 阶固有频率和振型Fig.14 First eight-order natural frequencies and modal shapes for a riser hinged at both ends

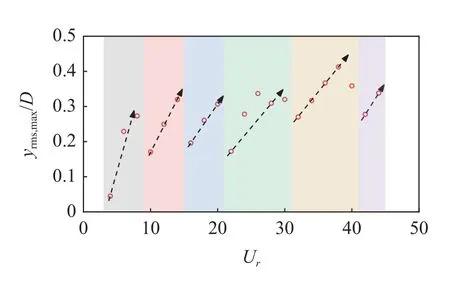
图15 沿立管展向最大的横向位移均方根值Fig.15 Maximum RMS amplitude of the transverse displacement along the riser span

横向振动的主导频率与1 阶固有频率的比值如图16 所示.同样地,振动频率的变化趋势与悬臂式立管也是一致的,即振动频率随着折合速度的增加而逐渐增大,并且当振动模态改变时,振动频率会出现较大幅度的增加.不同的是,在相同的折合速度区间内,两端铰支立管存在6 阶振动模态,而悬臂式立管只存在4 阶模态.这是由于两端铰支立管的1 阶固有频率较大,相同折合速度下其对应的真实来流速度更大,这导致两端铰支立管被激发出高阶模态响应.本文选取两端铰支立管的3 阶振动模态进行分析,该模态下3 个不同折合速度作用下的立管不同位置的振幅时空演化如图17 所示,选择的时间段均为5～7 s.可以发现,两端铰支的立管展向不同位置处的振幅均随折合速度增加而增大.在低阶模态响应下,随折合速度增加,该时间段内驻波特征逐渐增强.这两个特征与悬臂式立管是一致的.

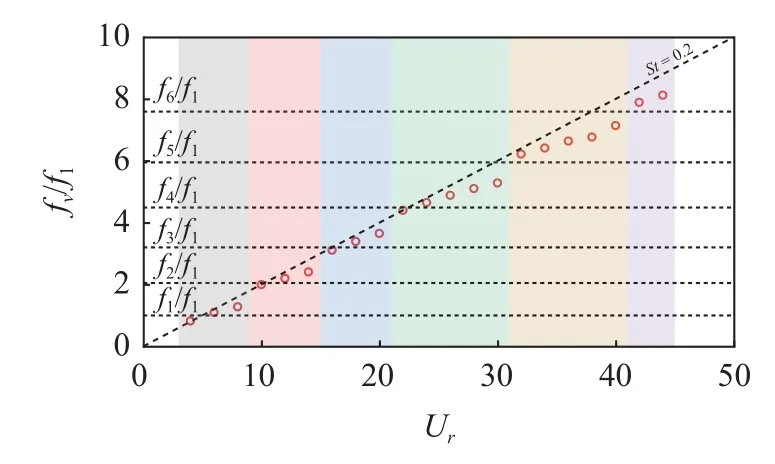
图16 立管横向振动的主导频率比Fig.16 Dominant frequency ratio of the transverse vibration for the riser

图17 立管不同位置的振幅时空演化 ((a)～(c) Ur=16～20)Fig.17 Temporal-spatial evolution of transverse vibration amplitude along the riser span ((a)～(c) Ur=16～20)

4 结论

矿产混输垂直提升管道是深海采矿集成系统中十分重要的装备,其悬臂式的结构面临复杂海洋环境时的振动特征不同于传统海洋立管,目前文献仍缺乏对该类型立管的讨论.本文的主要目的便是分析具有一定底部重量的悬臂式立管在不同来流速度下的涡激振动响应.为此,本文首先建立了基于切片法思想的DVM-FEM 耦合模型,通过数值计算两端铰支立管的振动响应并与模型试验结果对比,验证了该耦合模型的有效性.最后,系统性地分析了不同速度的均匀来流作用下悬臂式立管的横向振动响应特征,主要结论如下.

(1)本文采用的DVM-FEM 耦合算法可以准确预报柔性立管在不同速度下的振动模态,但振幅相比试验结果要小,该问题同样出现在前人的研究工作中[39].由于本文目的是研究深海采矿系统中存在的悬臂式立管的涡激振动特征,因此目前工作主要分析不同来流速度对这类特殊立管的影响规律,如何实现对立管实际振幅的准确预报仍有待进一步的研究.

(2)对于悬臂式立管,随着折合速度的增加,立管的振动模态阶数逐渐增加.同时,振动模态在一定的折合速度范围内是相同的.在同一模态下,立管不同位置的振幅随着速度增加而增大,尤其是无约束的立管底部会发生较大的位移.此外,当模态发生转换时,振幅会发生突降,并随着速度的增加振幅再一次逐渐增大.振幅随Ur和z/L的改变整体上呈现出波浪式的变化特征.

(3)深海采矿垂直提升立管底部与中间仓及输送软管相连接,因此底部位移对采矿系统整体稳定性有重要影响.本文结果表明,在同一振动模态下,悬臂式立管底部位移呈现出随折合速度线性变化的特征.当振动模态发生转变时,振动主导频率存在突然跳跃的特征.

(4)本文重点分析了3 阶振动模态下的悬臂式立管的振动响应.可以看出,振动主导频率在低折合速度下低于3 阶固有频率,随着速度增加,振动频率逐渐增大并远离3 阶固有频率.此外,无约束的立管底部的振动能量较大.对于本次研究中3 阶模态振动下的悬臂式立管,其驻波特征随着折合速度增加而逐渐加强,需要注意的是,本文关注的立管模型的长径比较小且为低阶模态响应,对于实尺度深海采矿立管以及高阶振动模态响应下的立管,其振动特征仍需进一步研究.

(5)本文对比了悬臂式立管与两端铰支立管的异同.可以发现,悬臂式立管的各阶固有频率均小于对应的两端铰支立管的固有频率.在相同折合速度区间内,两端铰支立管被激发出更高阶的振动模态响应.此外,两种类型立管的VIV 振幅和频率随折合速度的变化规律是相同的.

(6)垂直管道水力提升系统是深海采矿的主流方式,但目前仍缺乏对这类特殊的底部弱约束立管的数值与试验研究工作.未来研究工作可以考虑以下几方面:母船运动对悬臂式立管涡激振动和水动力性能的影响;中间仓重量改变的影响;考虑中间仓惯性力作用下的深海采矿立管模型的结构动力响应;海洋剪切流动等变化的影响;考虑内部流动的立管振动特征;采矿立管涡激振动抑制措施等.