片状颗粒间液桥力变化规律的计算研究1)

刘奉银 姜景希 李栋栋

(西安理工大学岩土工程研究所,西安 710048)

引言

非饱和土是由气体、液体、固体组成的多相体系[1].土水特征曲线描述了吸力与含水率之间的关系,是非饱和土力学中的基础本构关系,对于分析非饱和土持水性、渗透性、变形及强度特性具有重要意义.然而土水特征曲线具有增、减湿路径依赖性,反映了非饱和土增减湿过程中持水性能的变化,表现为相同吸力条件下土体中脱湿过程中赋存的水量比增湿过程多[2-4].

深入理解土水特征曲线滞回特性对非饱和土强度、变形、流动特性的影响,内因上从土性的角度涉及土的颗粒大小、级配、矿物成分、压实度以及水的含量、赋存状态与空间分布、孔隙气体的赋存状态(封闭、连通)与空间分布等因素,外因上需要考虑土体应力历史、应力大小、应力路径等因素[5-7].非饱和土中吸力和土水特征曲线的影响因素多,变化规律复杂,因此,固液作用机理亟待深入研究,然而仅通过宏观土样试验难以解释固液作用机理,因而从细观角度研究土颗粒与液体相互作用机理揭示其本质更有必要.颗粒间的作用力涉及短程双电层力、范德华力与毛细力(以下统称液桥力).饱和土随含水率降低进入非饱和状态,土中产生吸力,在高饱和度、低吸力条件下,土的力学特性发生剧烈变化,此时毛细水起主要作用.而在低饱和度、高吸力条件下,土体中含水率趋于稳定[8-11].因而针对土颗粒间液桥力变化规律及其影响因素开展研究,具有重要的理论意义.

颗粒间液桥力常用的计算模型有能量法、几何法、Young-Laplace 方程积分法[12].其中能量法有物理基础,能考虑液体体积、接触角的影响.几何法假定液桥轮廓线为圆形或抛物线形(目前缺乏物理依据),几何误差无法避免[13-14].1926 年,Fisher[15]提出环形近似方法,并对相互接触的颗粒系统中毛细作用进行了分析.Lian 等[16]指出基于环形近似的颈部法,在较大液桥体积、分离距离范围内的稳态液桥的计算液桥力误差小于10%,并基于最小能量原理确定了Young-Laplace 方程稳定数值解.Orr 等[17]基于椭圆积分求解Young-Laplace 方程,Nguyen 等[18]用微分几何的方法求解Young-Laplace 方程,Lambert和Delchambre[19]提出双重打靶法对Young-Laplace方程进行数值求解,同时系统阐述了基于能量法、几何法及拉普拉斯方程法的固体颗粒间液桥力模型.

此外,由于自然界中颗粒形状极其复杂,为了便于研究,深入理解非饱和土吸力特性的内在机理,将土颗粒简化为规则的球体颗粒或者片状颗粒.①当简化为球体颗粒时,Willett 等[20]利用微分天平测量了一对等径或不等径的球体颗粒间附着液体时的液桥力变化;Damiano 等[21]通过小挠度的悬臂装置,测量了一对等径球体颗粒间液桥力的大小;Diana 等[22]和Wang 等[23]在两颗粒拉伸试验的基础上进一步测量了三颗粒间液桥力的变化.②当简化为片状颗粒时,Sprakel 等[24]研究了在不同饱和度条件下平板和球面液桥的性质;庄大伟等[25]、朱朝飞等[26]分别从试验和理论分析的角度研究了狭长平板间液桥的形态.

软件模拟在一定程度上可以解决试验过程中具体条件无法准确控制以及理论公式推导中假设脱离物理本质的困局.由K.A.Brakke 教授及其团队整理的开源软件Surface Evolver,能极好地模拟固、液、气三相组成的各种稳定形态.王学卫和于洋[27]利用Surface Evolver 模拟了平面和不同曲率的球状表面之间液桥的拉伸直至断裂的动态过程;于洋等[28]进行了一对平面间的液桥拉伸-断裂试验研究,并利用Surface Evolver 进行了同条件下的液桥拉伸-断裂模拟,但缺少对液桥拉伸直至断裂过程中液桥力的研究.

上述关于固液相互作用的研究涉及理论、试验、模拟等多方面,且均取得了一定的成果.然而大多研究均集中在等径或不等径的球体颗粒,关于片状颗粒的液桥力在各参数影响下的变化规律研究不足.为此,选择以片状颗粒为研究对象,使用Surface Evolver 开源软件拟从最小表面能原理构建三维颗粒-液桥拉伸模型,分别对固液接触角、液桥体积、分离距离和钉扎效应等多因素影响下的液桥力变化规律展开讨论,同时与环形近似解对比验证.

1 计算模型与理论基础

1.1 片状颗粒间液桥力计算模型与假设

图1 为一对平行的片状颗粒间液桥的几何参数示意图,r为固液接触半径,R1为液桥颈部半径,R2为液桥颈部横截面外轮廓上一点的外切圆半径,s为两片状颗粒间分离距离,θ为固液接触角.

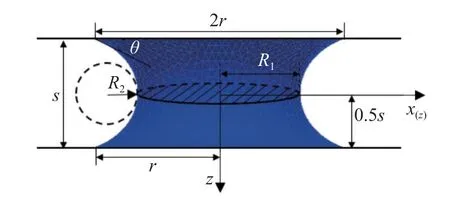
图1 一对片状颗粒间液桥几何参数Fig.1 Geometric parameters of liquid bridge between a pair of flaky particles

颗粒间液桥力与其形态密切相关,为了便于研究,此处有如下假设:

(1)片状颗粒在拉伸过程中彼此平行,且颗粒表面光滑无摩擦;

(2)液桥在颗粒间呈轴对称分布,且固液接触区域为圆形;

(3)假定液桥拉伸过程中弯液面形态为圆弧,不计重力,且固液接触角保持不变,体积守恒.

1.2 基于能量法的液桥力计算

在静态条件下,颗粒间液桥总是趋于收缩成具有最小表面能的形态,其间液桥力等于系统关于无限小位移的能量变化率的负值.由于忽略了重力势能,且液桥拉伸过程中液体体积恒定,即

液桥的表面能就是系统的总能量,因此,颗粒间液桥力计算公式为

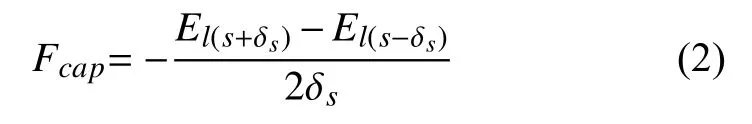
式中,E和El分别是准静态系统的最小总能量和最小表面能,s是颗粒间分离距离,δs是颗粒间微小位移,Fcap是颗粒间液桥力.

由于表面能与颗粒间液桥形态直接相关,为此,选择Surface Evolver 软件[29-30],基于所研究液体在给定条件下向系统总能量最小化状态演变的原理,模拟片状颗粒-液桥拉伸断裂过程.图2 是利用Surface Evolver 建立的片状颗粒-液桥三维重构模型,其间,上下部灰色区域是固体片状颗粒,中间蓝色区域为液桥.利用Young 方程cosθ=(σSV−σSL)/σ,其中,θ为固液接触角,σ,σSL,σSV分别是气液、固液、固气单位界面能,表示单位表面积所具有的自由能.系统的总能量表达式为

图2 片状颗粒-液桥三维重构模型Fig.2 Three-dimensional reconstruction model of plate-particle and liquid bridge

1.3 基于环形近似的液桥力计算

作用在片状颗粒上的液桥力Fcap由两部分组成,一部分是沿弯液面切线方向的表面张力分量,一部分是液体的内外压差,表达式为

式中,ΔP为气液界面内外压差,γ为液体的表面张力,θ是液体与两平面之间的接触角,r表示固液接触半径,如图1 所示.稳定时液桥的弯液面形态用Young-Laplace 方程[31]描述为

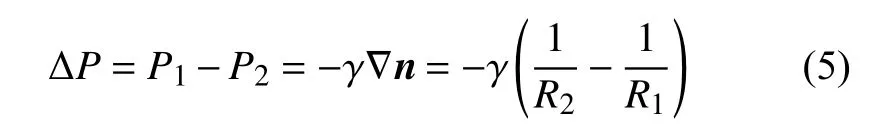
式中,P1为液体压强,P2为气体压强,n为指向表面外的单位法向量.根据文献[32]对液桥表面轮廓的数学描述,结合图1,液桥表面轮廓满足函数x=x(z),有

式中,H为由式(6)定义的液桥子午剖面的平均曲率.当假设液桥拉伸过程中弯液面形态为圆弧时,基于环形近似,同时将液体部分近似为圆柱体,圆柱半径取液桥颈部半径和固液接触半径的中间值时,可推得如下简化的液桥力表达式[33]为

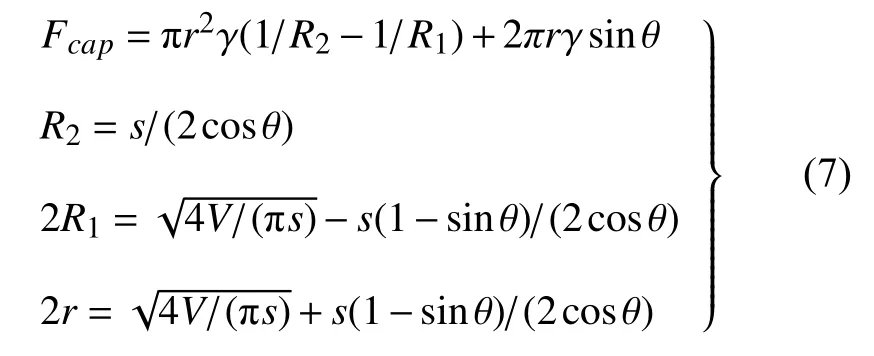
2 结果与讨论

根据建立的颗粒-液桥模型,液体为蒸馏水,γ=0.072 N/m,进行不同条件下的液桥拉伸模拟,其具体方案设计和材料参数如表1 所示.

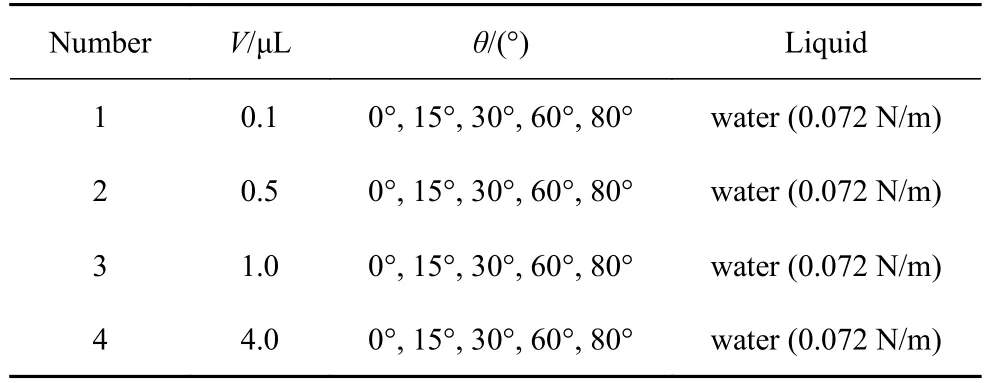
表1 方案设计与材料参数Table 1 Experimental design and the parameters of material

需要注意的是,下文中如果没有特别强调,则在模拟过程中颗粒-液桥系统的三相接触线是可以进行滑移的,从而保持固液接触角为常数.

2.1 液桥体积与固液接触角的影响

图3 是当固液接触角不变(此处,以θ=30°为例)时,不同分离距离下颗粒间液桥力随液桥体积的变化关系曲线.

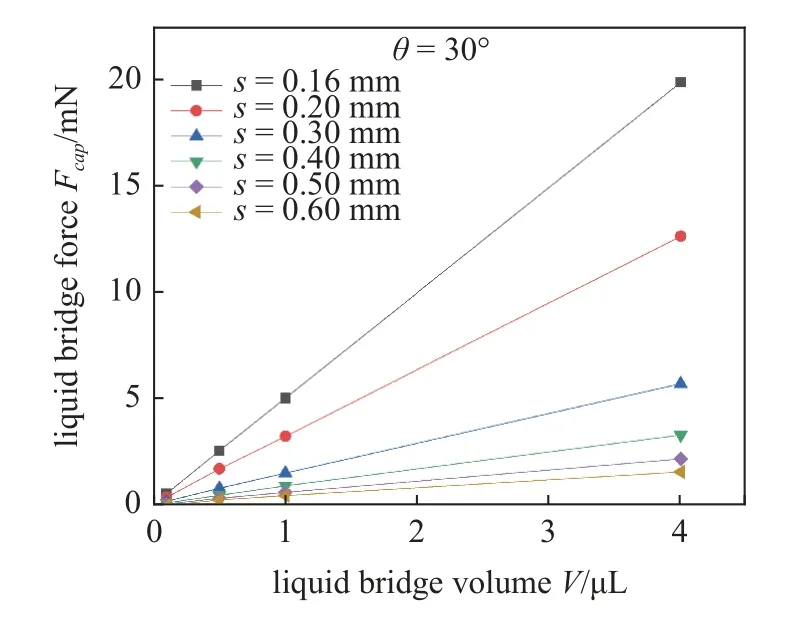
图3 固液接触角θ=30°时,片状颗粒间液桥力与分离距离和液桥体积的变化规律Fig.3 The evolution of the liquid bridge force between the flake particles,the separation distance and the volume of the liquid bridge,when the solid-liquid contact angle θ=30°

从图3 中可以看出,在其他条件相同时,随其间液桥体积的增大,片状颗粒间液桥力整体上呈线性递增的趋势.当两颗粒间的分离距离越小时,随着液桥体积的增加,其液桥力的变化幅度越大,变化速率越快,此结果与文献[34]中的描述一致,这是因为相同条件下,液桥体积增大时,液体与片状颗粒表面的浸润区域扩大,固液间黏附力增大,此时液桥颈部半径增加,液桥稳定性增强.

图4 是当液桥体积固定不变时,不同分离距离下颗粒间液桥力随固液接触角的变化曲线,其中,图4(a)～ 图4(c) 分别对应液桥的体积为0.1 μL,0.5 μL,1.0 μL.整体上看,液桥体积固定时,当颗粒间分离距离s<0.5 mm 时,随着固液接触角的增大,其液桥力逐渐降低,且降低的速率不断增大,这是因为接触角大小表示了液体对固体表面的浸润性大小,距离较小时,液桥力对接触角敏感度大,接触角越小,液体对该固体表面的浸润性越好,导致相同条件下液桥力越大;当颗粒间分离距离s≥0.5 mm 时,其液桥力值会随固液接触角的增加先增大然后缓慢降低,体积越小,这种现象越明显,且当分离距离越小,液桥力的变化幅度越大.这是因为,颗粒间距较大时,液桥力对接触角敏感度降低,导致液桥力变化小.

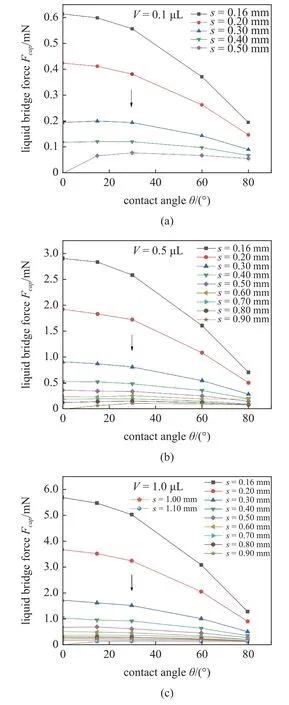
图4 固定液桥体积分别为(a) 0.1 μL;(b) 0.5 μL;(c) 1.0 μL 时的一系列分离距离下的液桥力随固液接触角的变化规律Fig.4 The capillary force evolution of a fixed liquid bridge with a fixed volume of (a) 0.1 μL (b) 0.5 μL and (c) 1.0 μL at a series of separation distances with solid-liquid contact angle was studied

2.2 拉伸过程中的液桥形态及接触半径

图5 为初始条件液桥体积V=2 μL,固液接触角θ=0°时液桥拉伸至断裂过程中的形态演变.其中,图5(a)是液桥在初始距离s=0.5 mm 时形成的稳定形态,此时的固液接触半径r=1.290 mm,颈部半径R1=1.108 mm,s<2R1,液桥呈现扁平型.随着颗粒间距离的增大,液桥被拉伸,其颈部收缩,固液接触区域变小,具体表现为颗粒-液桥系统的三相接触线在液桥被拉伸的过程中会向内产生滑移,即液桥为了维持自身的稳定性,需要不断地改变自身形态和位置,如图5(a)～ 图5(e)所展示的液桥形状变化,在这个过程中s<2R1,固液接触半径一直在减小,液桥均呈现扁平型.当颗粒间距离增加到1.0～1.2 mm 之间某一数值附近时,s=2R1,即液桥形态达到转折点,会呈现短暂的中间型,固液接触半径也达到最小值,此时的液桥形态介于图5(e)和图5(f)之间.此后,两颗粒不断分离,液桥颈部不断收缩,s>2R1,液桥形态呈现细长型,如图5(f)～ 图5(i)所示,固液接触区域不再内收,而开始向外扩张,即三相接触线开始向外滑移,接触半径增大.当颗粒间距接近断裂距离时,颗粒间液桥形态开始急剧变化,具体表现为:固液接触区域迅速扩张,液桥颈部急剧收缩,此时液桥处于极不稳定的状态,极其微小的扰动就会导致液桥断裂,断裂后的液桥会被分割成两部分,分别附着上下固体颗粒表面,并在自由状态下向外扩散达到新的稳定状态.

图5 V=2.0 μL,θ=0°时液桥拉伸过程中的形态演变Fig.5 Morphology evolution of liquid bridge during stretching at V=2.0 μL,θ=0°

为了定量化描述液桥拉伸过程中其形态和位置的变化,将液桥在拉伸过程中其子午剖面平均曲率、固液接触半径和颈部半径随分离距离的变化关系绘制如图6 所示.从图中可以看出,随着分离距离的增大,其平均曲率一直递减,且递减的速率开始时很快,随着颗粒间距增大逐渐变慢,接近断裂时递减的速率又急剧增加,而液桥颈部半径和平均曲率具有相同的变化趋势;不同的是,液桥在拉伸过程中其固液接触半径会先缓慢减小,而后会有一个短暂的基本稳定值,随后,又缓慢增大,接近断裂时会急剧增大.

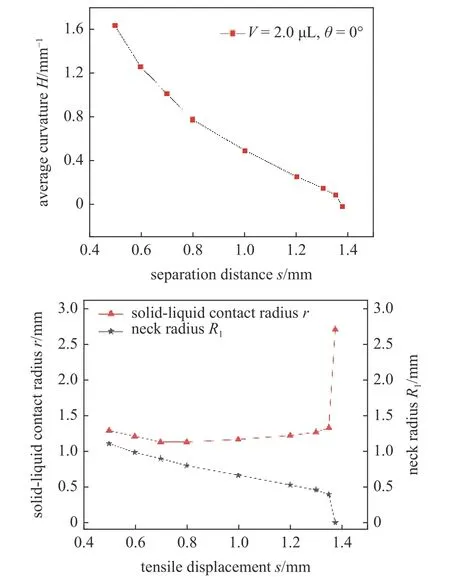
图6 V=2.0 μL,θ=0°时液桥拉伸过程中几何参数变化Fig.6 Geometric parameters change in liquid bridge stretching process with V=2.0 μL,θ=0°

2.3 自由滑移时液桥力的演化规律

图7(a)和图7(b)分别为恒定液桥体积下改变固液接触角和恒定固液接触角下改变液桥体积时其液桥力随颗粒间分离距离的关系曲线.从图中可以看出,所有条件下,颗粒间液桥力均在初始状态下处于最大值,随着其间分离距离的增加,其液桥力值不断降低,最后随着液桥的破裂而消失,且其液桥力降低的速率都是由快变慢,最后在接近断裂时又急剧增加.这与文献[34-35]所得结果一致,这是因为片状颗粒间分离距离的变化导致液桥形状发生改变,表现为液桥平均曲率改变及三相接触线不断滑移,如图6 所示,在这个过程中,液桥稳定性减弱,液桥力减小,直至颗粒间分离距离增加到一定值时液桥无法再保持稳定而断裂,液桥力消失.由此表明,片状黏土样孔隙越小,颗粒间相互作用力越强,越有利于黏土样吸持水分.

图7 不同条件下片状颗粒间液桥力随分离距离的变化规律Fig.7 The evolution of liquid-bridge capillary force with separation distance under different conditions

值得注意的是,对于图7(a),在恒定液桥体积为0.1 μL 的条件下,当颗粒间分离距离小于0.5 mm 时,固液接触角愈小的液桥力愈大;而当颗粒间分离距离大于0.5 mm 时,固液接触角愈大的液桥力愈大,这说明不同固液接触角对应的液桥力曲线随着分离距离的增加存在一个交点,而在这个交点前后,液桥力大小反转.对于图7(b),在恒定固液接触角为30°的条件下,体积为0.1 μL 的曲线整体最低,体积为4.0 μL 的曲线最高,且各曲线均表现出液桥力随着分离距离的增大而减小.

所有的初始颗粒间距均为0.16 mm,此条件下形成液桥,此时的液桥力记为初始液桥力,随后,增大颗粒间距,液桥被拉伸直至被拉断.值得注意的是,当颗粒间距较小时,微小的扰动便会引起其间液桥力值的剧烈变化,即变化速率大,而随着分离距离的增加,液桥力值的变化速率逐渐降低,直到液桥接近断裂时,其液桥力的变化速率会突然增大,而后趋近于0.如果将液桥断裂距离与其初始距离之间的差值记为液桥的总伸长量l,则液桥拉伸过程中的每一个位置处的伸长量记为ls,ls与l的比值记为拉伸率δ;同时,由于片状颗粒间的液桥力在初始位置处最大,其液桥的拉伸过程是液桥力的减小过程,则液桥力在拉伸过程中的损失率即为其初始液桥力与每一个分离距离下液桥力的差值对初始液桥力的比值.以图7(a)中的模拟结果为例,绘制出液桥力损失率与其对应伸长率之间的关系曲线,见图8,可以看出,当液桥伸长率接近30%时,其液桥力的损失已经高达50%以上,可见液桥力的损失主要集中在拉伸过程的前期.

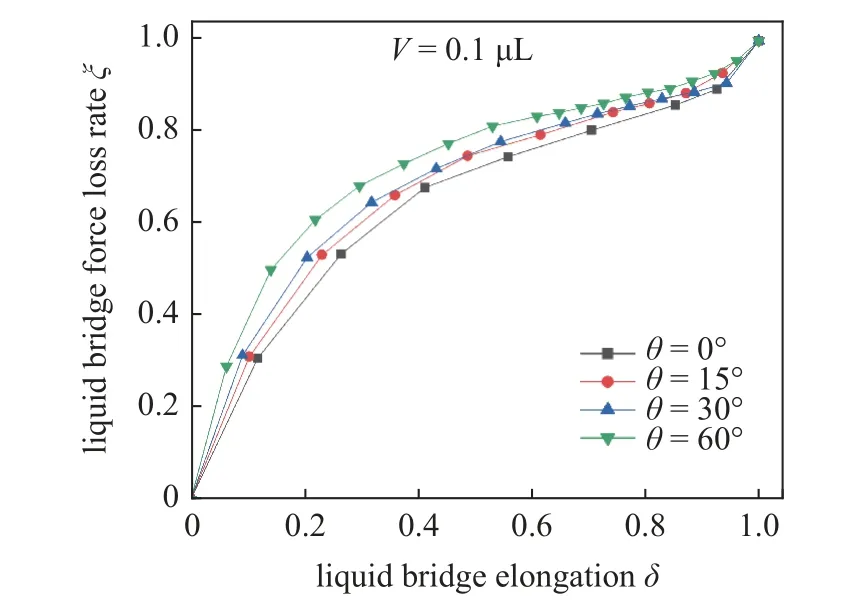
图8 V=0.1 μL 时颗粒间液桥损失率随伸长率的关系Fig.8 Relationship between loss ratio of liquid bridge between particles and elongation at 0.1 μL

2.4 钉扎效应对其液桥力的影响

从学者们的研究[36-37]发现,土水特征曲线存在滞回现象,究其原因,一方面是因为土体在增湿和减湿过程中接触角的不同,即接触角的滞后;另一方面则是因为土体内不规则的孔隙分布造成的毛细现象.其中,孔隙分布涉及非饱和土样的几何特征,而接触角滞后是滞回现象的微观机理.

在实际液桥拉伸过程中,由于物理或化学的不均匀性,固体颗粒表面并不光滑,致使液桥在被拉伸时并非一直在理想状态下滑移,而是阶段性地有钉扎效应.所谓钉扎效应,实际上是液桥在被拉伸过程中由于固体表面的束缚而导致其固液气三相接触线被约束在固体表面而局部不能向后退缩的现象,表现为接触角的滞后.当液桥钉扎时,其固液接触半径不变,而固液接触角变化;当液桥挣脱钉扎时,则固液接触角不变,而固液接触半径变化,即接触角的滞后会阻碍三相接触线的滑移[38-40].实际过程中一次完整的液桥拉伸其实伴随着液桥钉扎与退缩的交替进行,实际过程太过复杂,目前无法全部考虑,为方便研究,考虑主要因素的简化情况,即三相接触线一直处于钉扎状态下,液桥力随分离距离的变化规律.

图9 为给定液桥体积V=2.0 μL,并在自由滑移和钉扎两种状态下分别进行液桥拉伸的模拟结果.横坐标为拉伸过程中颗粒间分离距离,纵坐标为对应分离距离处液桥力的变化.从曲线结果看,在自由滑移状态下,对应于恒定的固液接触角,其液桥力随分离距离的增加一直递减;而在钉扎条件下,对应于恒定的固液接触半径,其液桥力随分离距离的增加先增大,直到峰值出现,随后一直递减.两种状态下的模拟结果对比表明,液桥钉扎的特征在于力随分离距离的增加存在一个峰值,这是因为钉扎效应使得液桥在被拉伸过程中无法向内或向外滑移以调整自身的稳定性,而使接触角发生跳跃变化,导致液桥力受接触角与分离距离共同主导,液桥稳定性较差,不利于片状黏土颗粒持水.

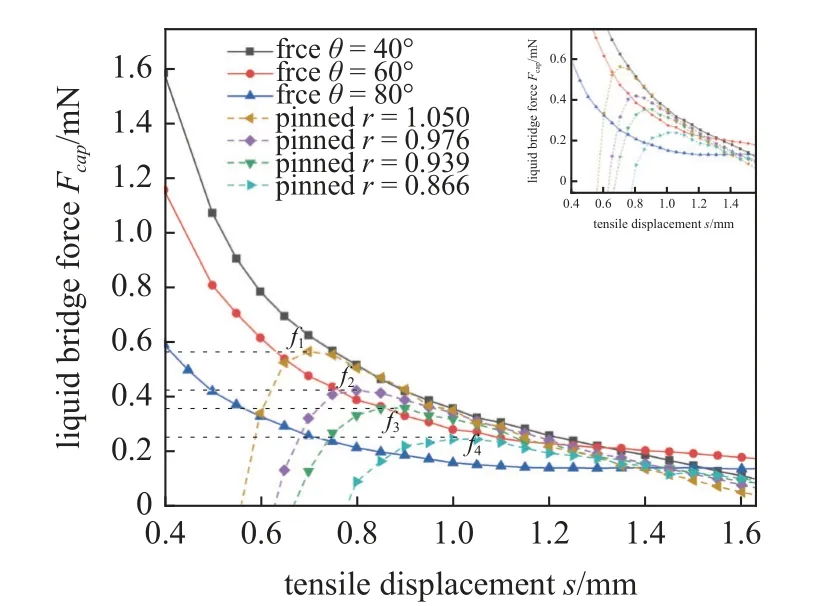
图9 液桥钉扎和自由滑移下液桥力的变化Fig.9 Evolution of liquid-bridge forces under hydraulic bridge nailing and free slip

如图9,在固液接触半径分别为1.050 mm,0.976 mm,0.939 mm,0.866 mm 时,其对应的液桥力峰值点分别为f1,f2,f3,f4,可以看出,液桥钉扎的范围越大,其液桥力峰值就越高,随距离的增加出现的也就越早,随着分离距离的增加,为适应分离距离的变化,其固液接触角会不断发生调整;与之对应的是液桥处于自由滑移状态时,增加分离距离会使三相接触线前进或后退,具体表现为固液接触半径会不断减小至最小值,随后保持基本稳定,在接近断裂时迅速增大,如图6(b)所示.由此可知,液桥钉扎效应的产生会影响液桥的稳定性,使液桥力减小,削弱颗粒间相互作用,不利于片状黏土颗粒吸持水分.

2.5 与环形近似解的对比分析

上述结果是基于Surface Evolver 从能量角度对片状颗粒间液桥力的数值解,为了分析模拟结果的可靠性,将对液桥体积V=1.0 μL,液桥处于自由滑移状态下拉伸的结果为例,与同条件下的环形近似解[33]进行对比分析,环形近似的相关理论如1.3 小节内容所述.液桥力采用式(7)计算,计算结果和数值解的对比见图10(a).

从图中可以看出,数值解和已有的环形近似解整体规律一致,且对于不同的固液接触角以及不同的分离距离范围内二者在数值上相差不大.对图10(a)中的结果进行误差分析,绘制如图10(b)所示的相对误差随液桥拉伸率的关系曲线.其中,当θ=60°和θ=80°,数值解和环形近似解在断裂前整个拉伸过程中的结果都具有极好的一致性,二者之间的误差相对于环形近似解基本上在6%以内,在断裂前,二者的误差急剧增加;当固液接触角θ为0°,15°,30°,液桥的拉伸率在10% 以内时,二者的误差基本在6%以下,而随着液桥拉伸率的增加,其误差会不断增大,当增加到30%时,二者之间的最大误差会迅速增加到40%.

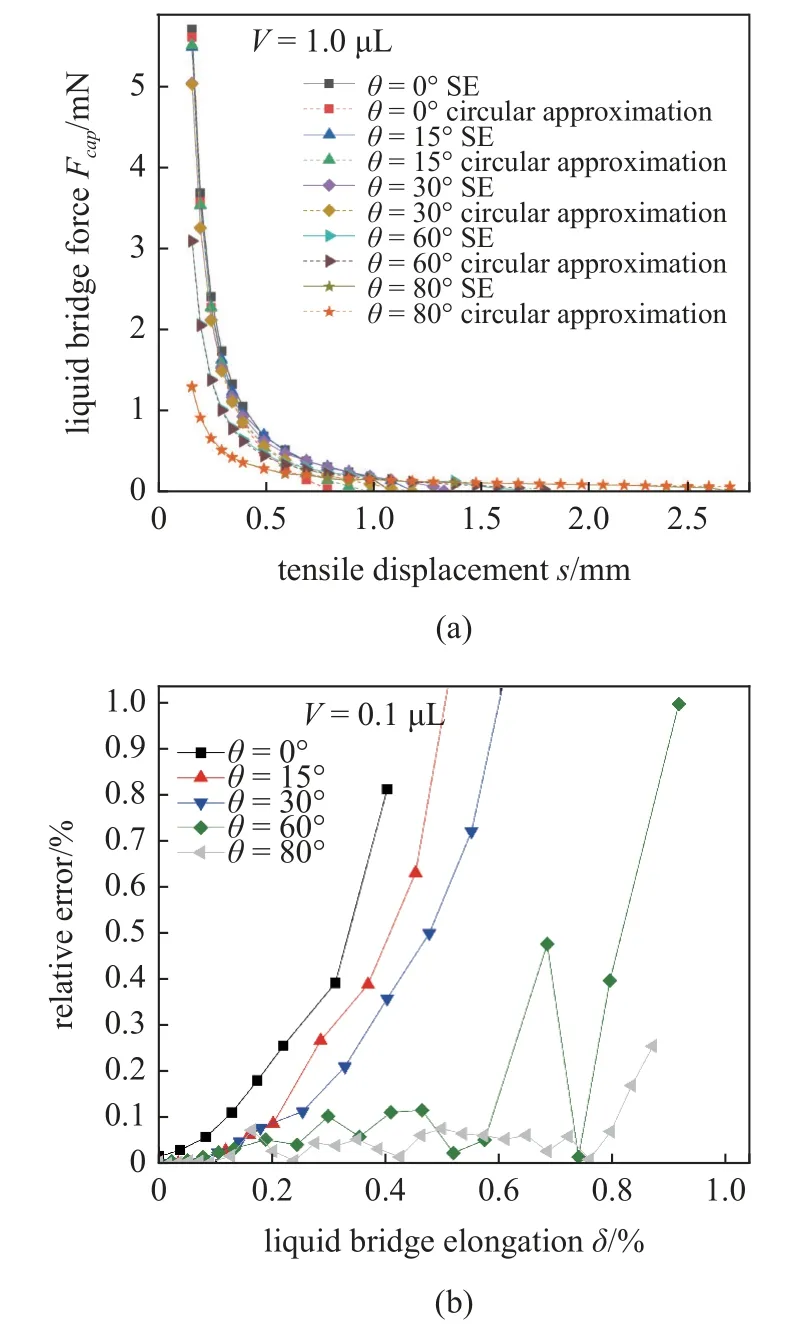
图10 恒定液桥体积为1.0 μL,不同固-液接触角下其(a)液桥力的数值解和环形近似解的对比及其(b)误差分析Fig.10 Comparison of (a) numerical solution and annular approximate solution and (b) its error analysis when the constant liquid bridge volume is 1.0 μL,the liquid bridge force at different solid-liquid contact angles

对于上述现象,是由于环形近似并不能完整描述整个液桥拉伸过程中其外轮廓的形态变化,实际中液桥只有在小距离时其外轮廓比较接近于环形,而随着颗粒间距离的增加,液桥被拉长,颈部收缩,其外部轮廓的形态会逐渐偏离环形,且颗粒间距越大,这种偏离程度会越严重,当接近最大分离距离时,液桥形态变得极不稳定,具体表现为其颈部收缩加剧.另一方面,接触角越小时,固体颗粒对液桥的影响越大,即在拉伸的过程中液桥越不稳定,所以表现为接触角越小时,液桥力的数值解和环形近似解的误差越大.

3 结论

利用开源软件Surface Evolver 通过最小表面能原理建立了片状颗粒-液桥三维模型,在此基础上系统地研究了液桥体积在0.1～ 4.0 μL,接触角在0～80°条件下,液桥力与固液接触半径的变化规律,并与环形近似解进行了比较;同时,还研究了钉扎效应对模拟结果的影响,结论如下.

(1) 片状颗粒间在初始位置处(初始间距0.16 mm)存在峰值液桥力,最大液桥力在0.197～21.831 mN 之间内变化,其中,当固液接触角为80°,液桥体积为0.1 μL 时,峰值液桥力有最小值0.197 mN;当固液接触角为0°,液桥体积为0.1 μL 时,峰值液桥力有最大值21.831 mN.

(2) 片状颗粒间液桥在拉伸过程中,其固液接触半径均先呈现递减的趋势,而后保持水平,随后在接近断裂时急剧增大;与此同时,随着分离距离的增加,液桥形态会经历扁平型、中间型和细长型三种形态变化.

(3) 当其他条件相同时,片状颗粒间液桥力在一定范围内随其体积的增大基本呈现线性递增;随分离距离的增大呈现递减的趋势,且递增的速率先快后慢;随固液接触角的增大先增后减或一直递减.

(4) 液桥体积一定时,在钉扎状态下,其液桥力会随着分离距离的增大迅速递增达到峰值,而后逐渐降低.