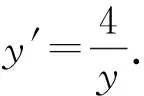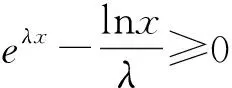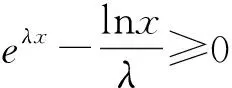多视角下同构法的应用*

福建省泉州市第七中学 (362000) 吴宝树 黄永生 林志敏

在一些数学试题命制过程中，命题者预设考察模型，并对考察模型中的变量多次赋值，使考察对象的结构复杂化，从而提升试题的难度.考生若能通过观察、变形找到命题者构造的模型，那么解题效率将大大提升.找到这个模型的方法，称为同构法.本文从同构法应用出发，呈现高中数学若干板块中常见的同构式，总结解题策略，希望对读者有所启迪.

应用一 方程组的解

例1 设x,y∈R,满足

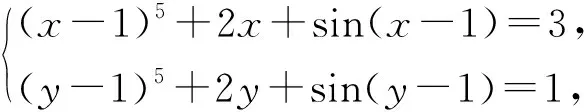
A.0 B.2 C.4 D.6

解析：原方程组变形为

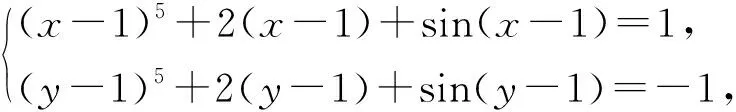
评析：对于结构相同的方程f(a)=0和f(b)=0，a,b可视为方程f(x)=0的两根.解题时可通过观察，将方程组变形得到同构式，进而构造函数.

应用二 数列的通项

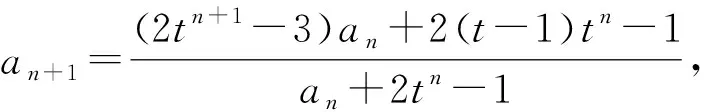
评析：数列中可将递推公式变形为“依序同构”的特征，即关于(an，n)与(an+1，n+1)的同构式,从而构造新数列便于求解.

应用三 不等式

例3 若0

A.ex2-ex1>lnx2-lnx1B.ex1-ex2>lnx2-lnx1

C.x2ex1>x1ex2D.x2ex1

评析：如果不等式的两边呈现同构特征，则可将相同的结构构造为一个函数，利用函数的单调性解题.

应用四 圆锥曲线的切线弦

例4 过直线x-2y+13=0上一动点A(A不在y轴上)作抛物线y2=8x的两条切线，切点为M,N,证明直线MN恒过定点.

评析：在解析几何中，如果A(x1,y1),B(x2,y2)满足的方程为同构式，则AB为方程所表示曲线上的两点.特别地，若满足的方程是直线方程，则该方程即为直线AB的方程.

应用五 指数与对数的互化