两种视角审视一类平面向量问题

江苏省昆山市柏庐高级中学 (215300) 汪 梅

数学是关于数量关系和空间形式的一门科学，向量兼具代数与几何的双重身份，是解决数学问题的基本工具，也是进一步学习和研究其它数学问题领域的基础，在解决问题中发挥重要作用.在高中数学的学习中，与向量有关的面积比问题频频出现，其中有一类与平面向量线性表示相关的面积比问题可以利用共线向量定理和建立平面直角坐标系即坐标法两种方法解决，这类问题在数学试题中属于中档题或难题，也是学生易错点甚至是盲点.笔者对该类问题进行初步研究并总结整理成文，供大家在课堂教学中借鉴参考.

一、问题呈现

思路探寻：为解决面积比问题，需确定点P的位置.

思路1 直觉思维：直觉思维是指对一个问题未经逐步分析 ，仅依据内因的感知迅速地对问题答案作出判断、猜想、设想.

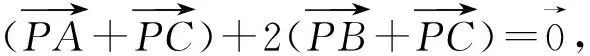
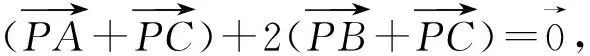
图1

评注：从系数的特征入手,从特殊的数据出发，找到了三点共线，从而问题得到解决,即关注系数的特征.

思路2 转换视角： 我们知道笛卡尔建立的平面直角坐标系架起了几何与代数的桥梁，那么本题能不能用代数的方法解决这个几何问题呢？我们知道解答填空题有更简便的方法,可以将问题特殊化：将△ABC特殊化为等腰直角三角形，通过建立平面直角坐标系即坐标法解决问题.

图2

评注：第一种角度是从系数的数据的特殊性出发，第二种角度是从特殊的三角形出发，体现了数与形的特殊性，可解决一类高考填空题，拓宽了我们的视野，灵活了我们的思路.

二、问题升华

思路1 构造三点共线

图3

评注：妙用“x+y=1”，构造三点共线，水到渠成.

思路2 三角形特殊化毕竟是解决填空题的好方法，但存在题型的局限性，下面采取非特殊化建系解决

图4

三、归纳、总结提升——问题的推广与探究

图5

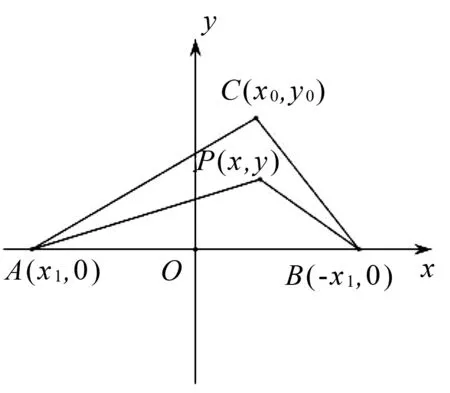
图6

四、变式训练、建构内化——问题的迁移与思路的加深

图7

从不同的角度入手，下面提供两种解法.

图8

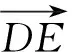
图9

五、结语