基于里程计/LiDAR/GNSS 的室内外连续定位方法研究*

钱 伟陈 析陈 鑫孙丙宇*

(1.重庆三峡学院机械工程学院，重庆 404130；2.中国科学院合肥物质科学研究院，安徽 合肥 230031)

随着制造业与物流行业的飞速发展，市场对自动导引车(Automatic guided Vehicle，AGV)定位导航的需求逐渐扩大，其中室内外连续定位技术需求更是日益爆增[1－2]。 室内外连续定位技术已经独立于室内定位，成为导航定位领域的一个新的研究方向。室内外连续定位方法以定位精度高、稳定性好、环境适应性强为特点，其核心算法在于室内和室外融合定位算法与定位信号源平滑滤波算法。 然而受室内外光照、遮挡物等变化和不平滑的定位信号源切换的影响，在实际室内外连续定位过程中易出现定位信号丢失、定位信号精度差等问题，极大地影响了AGV 在室内外连续场景的定位导航。 因此，如何实现稳定性高、精度高的AGV 室内外连续定位算法，成为了AGV 定位导航工程应用中的一个研究热点。

基于激光雷达的信标定位算法是当前室内定位领域热点算法之一[3]。 在室内定位过程中，激光信标定位算法相对于RFID、WIFI、激光即时定位与地图构建(simultaneous localization and mapping，SLAM)、视觉SLAM 等[4]室内定位算法具有定位精度高、定位平稳、鲁棒性高等显著优势。 在市场对室内外连续定位的高需求下，基于激光信标、全球导航卫星系统(Global Navigation Satellite System，GNSS)、里程计组合实现AGV 室内外连续定位，具有巨大的潜在应用价值。 传统室内外连续定位算法种类较多，如文献[5]提出了一种基于UWB 协助低成本惯性测量单元(IMU)系统的连续定位解决方案，评估移动机器人的位置、速度和位姿。 文献[6]提出了一种室内外连续定位系统，该系统考虑了UWB、GPS 以及两种定位技术的结合，并可靠地估计在室内和室外场景中移动的车辆的位置。 文献[7]提出一种基于GPS/INS/磁力计进行多传感器融合的室内外连续定位方法，定位轨迹误差在2 m 以内。综上所述，传统室内外连续定位算法，定位精度大都在米级，信号源切换实时性较差，定位服务适应对象为手机、人类等，不能满足AGV 定位精度、稳定性的要求。

基于此背景，AGV 室内外连续定位技术要解决的技术难题在于室内外定位精度问题和不同定位信号源平滑跳转问题。 在室内外连续定位领域，本文首次提出一种基于里程计/激光雷达(Light Detection and Ranging，LiDAR)/GNSS 的多元异构数据融合方法解决室内外定位精度问题，提出一种基于扩展卡尔曼滤波的多模型融合连续定位方法，利用GNSS 和LiDAR 协方差、水平精度因子动态计算定位信号源概率，借助定位信号源概率实现不同信号源的平滑跳转，从而提高室内外连续定位系统的稳定性和定位精确，满足AGV 的定位导航要求。

1 室内外高精度定位

1.1 室内外连续定位算法框架

本文针对传统AGV 在室内外不同动态环境下工作易出现定位丢失，定位精度下降的问题，提出了一种AGV 室内外连续定位算法，原理如图1 所示。 是一种基于扩展卡尔曼滤波的多元异构融合定位算法，采集了来自里程计、GNSS、LiDAR 的数据。 利用里程计获取实时6 轴角速度、加速度，并通过积分运算实时推算AGV 实时速度和位姿，并提取姿态矩阵。 然而由于定位信息是通过积分运算进行的，里程计长时运行会产生严重的误差漂移。 本文采用扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法来提高室内外连续定位精度，算法系统方程由里程计提供参数更新，量测方程分两段式进行更新，室内环境时由LiDAR 信标算法提供更新，室外环境由GNSS 提供参数计算更新，同时提出了一种基于扩展卡尔曼滤波的多模型融合连续定位滤波方法，提高信号源切换的平滑性。

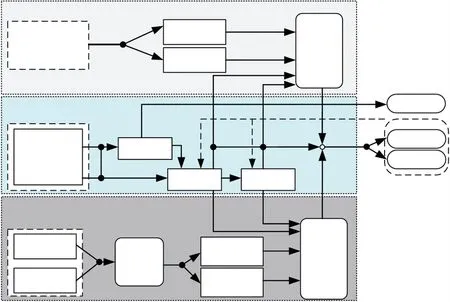
图1 组合定位原理图

AGV 室内外连续定位过程开始时，自动获取上一时刻定位状态估计，并通过里程计进行速度积分和位姿积分，更新系统方程。 室外情况下，GNSS 接收机获取AGV 定位数据计算量测方程，采集传感器协方差矩阵计算卡尔曼增益系数，并更新AGV 的姿态最优估计；室内情况下，采用LiDAR 信标定位算法计算AGV 定位数据，更新量测方程，并实时更新卡尔曼增益系数，更新AGV 姿态最优估计。 AGV最优估计作为下一时刻系统方程初始位姿，循环迭代，实现AGV 室内外的连续定位。

1.2 基于EKF 室内外融合定位算法

在室内外连续定位场景下，障碍物遮挡、动态环境改变的问题难以避免，为了获取更准确的AGV 位姿，本文采用扩展卡尔曼滤波(EKF)进行多传感器信息融合。 由于系统状态变量和测量数据间的关系是非线性的，需要将非线性问题转化为线性问题，其中扩展卡尔曼滤波(EKF)使用泰勒展开式来解决转化问题，再根据最小均方差规则进行系统状态的最优估计[8]，求解最优估计的流程如图2 所示，YLk为LiDAR 信标定位算法计算室内环境量测方程，YGk为GNSS-RTK 计算室外环境量测方程，Yk为最优量测估计，Xk为最优预测估计，Uk为里程计增量，＾Xk为后验最优估计。

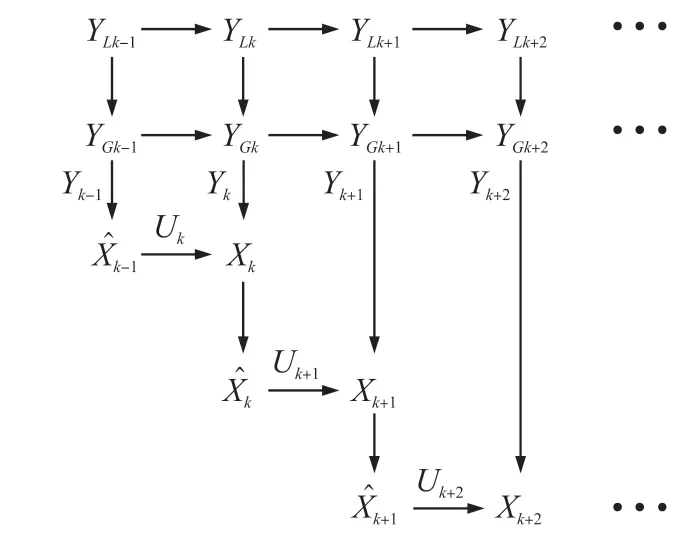
图2 最优定位估计

里程计模型建立系统状态方程，由于里程计存在累计误差较大，需提供量测方程进行误差修正更新:

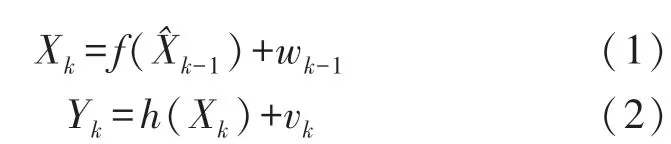
对式(1)和式(2)进行线性化处理，采用雅克比矩阵来替代系统方程的非线性转移过程。H表示h的雅克比矩阵，F表示f的雅克比矩阵。 雅克比矩阵求解方式为方程矩阵对变量的偏导数。

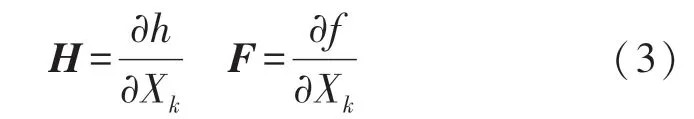
式(1)和式(2)系统状态方程和量测方程线性化具体表达式为:

式中:Xk、Xk－1分别为k时刻与k－1 时刻的状态变量，p为位置，v为速度，θ为航向角；f表示非线性系统模型；wk－1考虑为系统噪声，假定噪声均值为0，Rk为协方差。Yk表示实时最优量测方程，h表示非线性观测模型，vk表示量测噪声，考虑量测噪声是均值为0，协方差为Qk的高斯噪声。为系统状态转移系数矩阵，T为AGV间隔采样时间；H＝为量测系数矩阵，θ为观测航迹与推算航迹的夹角，Vx、Vy为k时AGV 速度。 系统状态预测量计算的协方差矩阵:

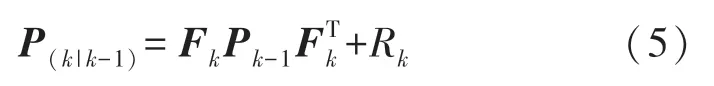
计算AGV 预测信息与量测信息后，更新此时AGV 状态的后验概率分布。 AGV 系统在时刻k时的扩展卡尔曼滤波增益为:

由量测信息对预测信息进行更新:

最后再次更新后验协方差矩阵:

通过上式可以理解AGV 的系统运动模型迭代更新过程。 根据前一时刻的状态Xk－1获取AGV 先验状态X(k｜k－1)及其协方差矩阵P(k｜k－1)。 计算出k时刻扩展卡尔曼滤波的增益系数后，可更新k时刻AGV 的后验最优估计X(k｜k)及其协方差矩阵P(k｜k)。因此，在数据融合定位中，随着量测数据的不断输入，AGV 状态参数将不断迭代更新，实现AGV 的实时高精度定位。

2 室内外定位平滑滤波

2.1 基于SVD 坐标变换

根据1.1 设计多传感器融合实现连续定位，需设计算法将GNSS、LiDAR、里程计定位转换到同一全局静态坐标系下。 另外因为传感器外形尺寸影响，需要将传感器转换到AGV 上同一位置。 本文室内外坐标系统具体如图3 所示。

图3 AGV 多传感器坐标系

图中XOY 为LiDAR 定位坐标系；X′O′Y′为GNSS-RTK 定位坐标系；X″O″Y″为AGV 车身坐标系，同时也是里程计坐标系。 AGV 运动轨迹由室内经过混合场景到达室外，GNSS-RTK、LiDAR 均可以提供混合场景下的AGV 定位。Pi为AGV 在混合场景中里程计处定位点，Pi在XOY坐标系下坐标为PLi＝(XLi，YLi)，在X′O′Y′坐标系下坐标为PGi＝(XGi，YGi)，传感器安装位置1，2，3 处于AGV 中轴线上，位置1 与2 相距d1，位置2 与3 相距d2，α为AGV 航向角。 多传感器坐标系统转换步骤如下:

步骤1 将LiDAR 定位数据由雷达安装位置1P′Li，转换到里程计安装位置2PLi:

步骤2 将GNSS 接收机定位数据由接收机安装位置3P′Gi，转换到里程计安装位置2PGi:

步骤3 将GNSS、LiDAR 定位数据统一到同一静态坐标系下，将LiDARPLi转移到GNSSPGi坐标系下，采用SVD 统计方法计算坐标系平移矩阵T(a，b)、旋转矩阵R:

坐标转换误差Ei分析结果:

定义标定多对点坐标质心公式:

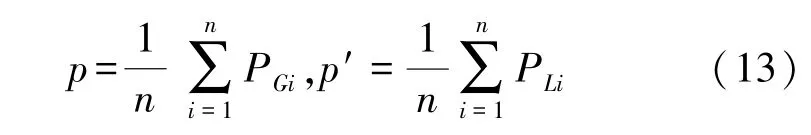
使误差最小的R和T就是最优的旋转矩阵和平移向量，利用多对点构造最小二乘:

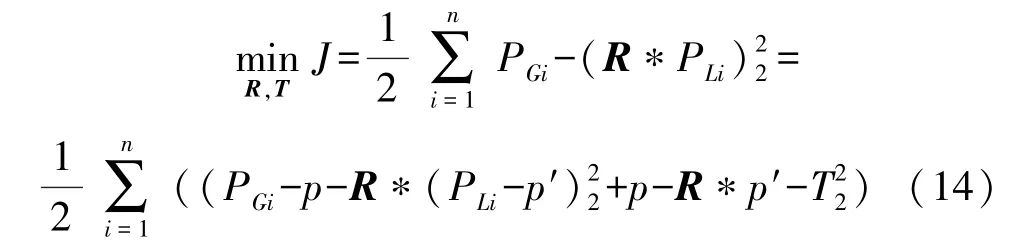
式中:第一项只与旋转矩阵R有关，第二项与R和平移向量T都有关。 可以令第一项为0 求得R，再令第二项为0 求得T求PGi去质心点:

最终计算旋转矩阵R、平移矩阵T:

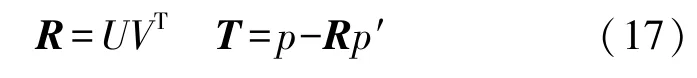
2.2 室内外信号源平滑滤波

为了提高室内外连续定位稳定性和精确度，研究人员最关心的热点在于定位信号源切换频率、信号源切换是否造成定位精度下降。 如果室内外信号源平滑滤波算法较差，将严重影响组合定位的稳定性和精度。 本文提出一种基于卡尔曼滤波的信号源平滑滤波算法，在室内外连续定位中，AGV 定位的稳定性、精度均有较明显提高。 室外环境下，GNSS协方差矩阵，水平精度因子均可以有效评估GNSS定位的准确度和稳定性[9－10]；室内环境下，雷达连续多帧扫描到信标数、雷达信标定位算法协方差都可以直接有效地反映室内雷达定位的精度和稳定性。

其中GNSS 水平精度因子(HDOP)计算公式如式(18)，hii是权重矩阵H的对角元素。αKn和θKn分别代表卫星方位角和俯仰角

定位信号源最优概率估计由GNSS、LiDAR 协方差矩阵、水平精度因子、LiDAR 信标数等共同推算，具体算法如表1。

表1 室内外信号源平滑滤波算法

3 实验

3.1 实验条件和环境

本文提出室内外连续定位算法，在合肥某园区进行了AGV 的室内外连续定位实验，以评估室内外连续的定位稳定性和精度。

图4(a)所示为麦克纳姆轮实验平台，搭载SICK-NAV 型雷达、司南M600-GNSS 定位系统，实验场景下GNSS、LiDAR 安装在带有里程计的麦克纳姆轮实验小车上，并在GNSS失效区域布置好雷达定位信标，室外无遮挡处安装GNSS 主机站和电台。

如图4(b)所示，LiDAR 信标用实线圈出，实验开始定位进行对准，因为里程计进行轨迹推算需要初始位姿变量，初始位姿在室内外分别由精度较高的LiDAR 信标定位算法或者GNSS-RTK 计算。 完成初始对准后，测试平台开始进行室内外连续定位测试。

图4 麦克纳姆轮实验平台和实验场地

本实验共采集8 次数据，如表2 所示。 其中实验1～8 分别为室内定位采集、室外定位采集、室内外连续定位采集、室内外随机定位采集。 实验数据的采集与室内外连续定位算法实现均在笔记本电脑(Intel i5-9300H CPU＠2.4 GHz，16G RAM)上运行。

表2 采集数据集

3.2 实验结果

根据3.1 采集数据集，选取实验5 进行室内外连续定位算法精度与稳定性分析。 测试平台实验定位轨迹如图5 所示，虚线为相对真值轨迹，由GNSS、LiDAR 静态定位采集拟合；实线为最终室内外连续定位算法计算轨迹。

图5 实验环境和实验轨迹图

图6为麦克纳姆轮测试平台实验过程中LiDAR接收雷达信标数和GNSS 从站接收卫星数随时间变化图。 其中0～90 s 和230 s～726 s 测试平台处于室外环境；90 s～230 s 测试平台处于室内环境。 可以看出室外向室内移动过程中，从站接收卫星数减少，GNSS 定位精度降低，同时雷达扫描信标增多，LiDAR 定位精度提高；室内向室外行进过程中，从站接收卫星数增加，GNSS 定位精度提高，同时LiDAR 扫描信标减少定位精度降低

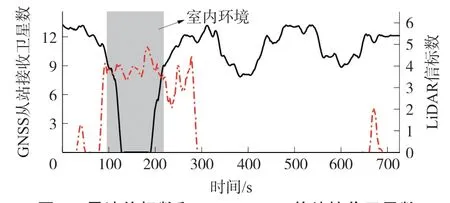
图6 雷达信标数和GNSS-RTK 从站接收卫星数

表3 为室内外连续定位平均误差对比。 可以发现在定位效果上，本文提出GNSS、LiDAR、里程计连续定位系统相比传统室内外连续定位方法[7－8，11]，定位精度上具有较大提升。 平均绝对定位误差为0.122 m，满足AGV 的室内外连续定位导航需求。

表3 不同组合定位平均误差

图7 所示为本次室内外连续定位实验的定位误差绘图，系统在只有GNSS/里程计融合定位下，室外具有较好的定位精度，室内定位基本丢失；在只有Li-DAR/里程计定位情况下，室内具有较高的定位精度，室外环境下定位基本丢失。 本文提出室内外连续定位方法，系统可以自适应地切换定位模型，连续定位误差明显减小，最大绝对定位误差为0.5 m，平均绝对定位误差为0.122 m。 对比传统室内外连续定位方法[12－15]，在定位精度和稳定性上均有明显提高。

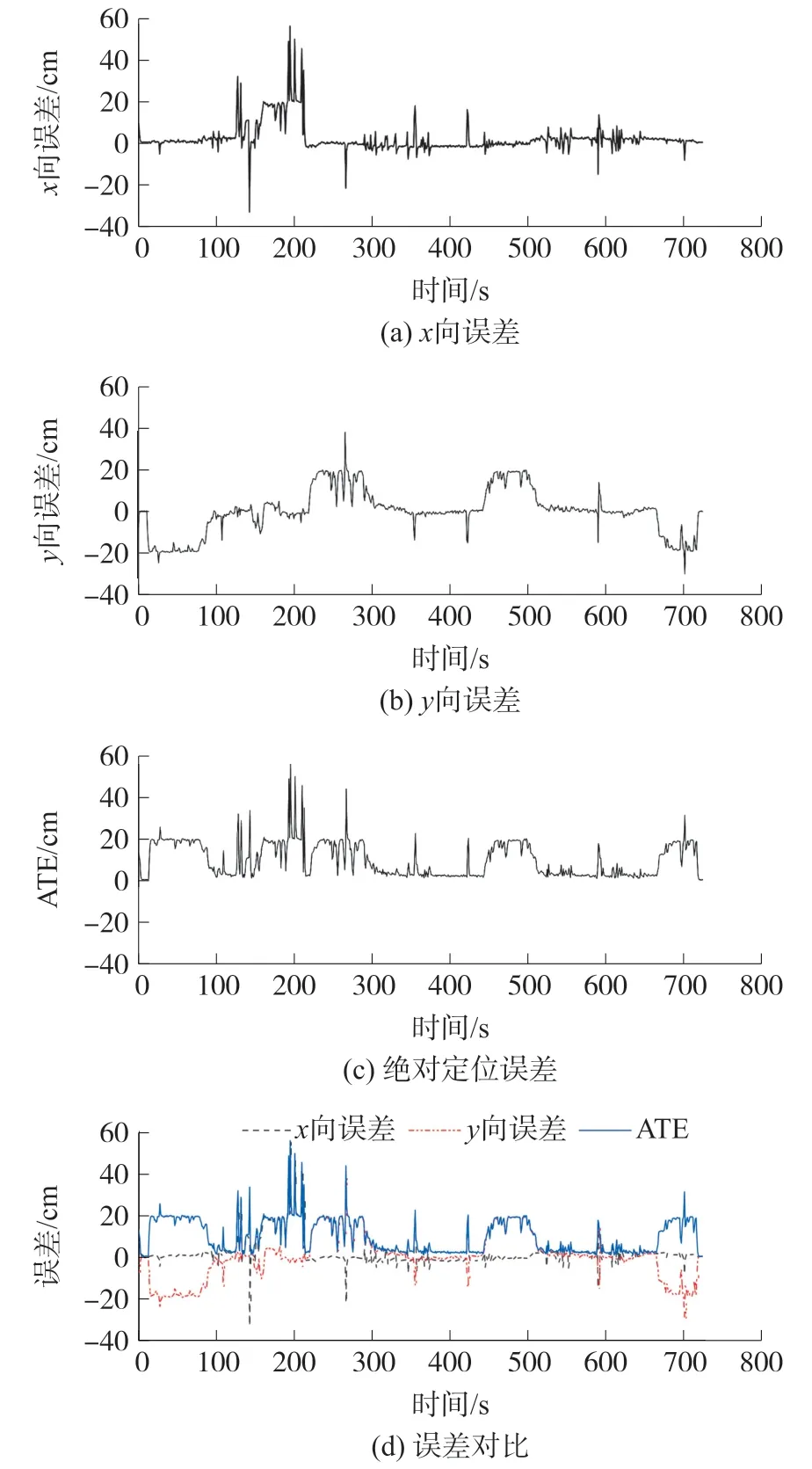
图7 室内外连续定位实验定位误差图

4 结论

本文首次提出了一种基于里程计、LiDAR、GNSS 融合的室内外连续定位方法，通过建立室内雷达信标数据库和室外GNSS-RTK 定位基站，实现AGV 的全局定位。 针对室内外遮挡物和光照改变造成AGV 定位精度、稳定性降低的问题，本文首次提出了一种室内融合LiDAR/里程计、室外融合GNSS/里程计的全局定位方法；同时为了抑制因为信号源切换造成定位稳定性下降的问题，提出了一种室内外信号源平滑滤波算法，该方法利用LiDAR、GNSS 定位协方差、GNSS 水平定位精度因子、LiDAR扫描信标等评估信号源可信度，剔除不可信定位结果。 最后，通过实际实验验证了所提出方法的有效性。