基于经验模态－小波包分解和卷积神经网络的P300 脑电信号分类研究*

崔丽丽郑 赟孟小飞马玉良*

(1.杭州电子科技大学采购中心，浙江 杭州 310018；2.杭州电子科技大学自动化学院，浙江 杭州 310018)

脑机接口(Brain-Computer Interface，BCI)是一种特殊的人机交互接口，它可以在大脑与计算机等外部设备之间建立一条可靠的通信链路，通过采集与处理脑电信号以实现人体与周围环境的交流。 在众多的脑电信号中，P300 信号凭借其良好的特性，受到了越来越多研究人员的青睐[1]。

P300 信号是由小概率事件诱发的脑电信号，它是一种内源性的事件相关电位(Event-Related Potential，ERP)，与大脑的认知功能相关。 P300 信号和外部刺激之间具有严格的锁时性，在刺激发生后约300 ms 时刻会产生一个正电位波形，因此可以作为BCI 系统的控制信号[2]。 脑机接口中一般使用oddball 实验范式(一项实验中对同一感觉通道施加两种刺激，两种刺激出现的概率差异极大)来诱发用户产生P300 信号[3]。 许多学者对P300 信号在字符拼写、命令输出等BCI 系统中的应用进行了积极的探索，并取得了一定的成果[4－6]。 但由于P300信号具有非线性、非平稳性及个体差异性等特点，大部分研究仍处于实验阶段。 如何高效地对P300 信号进行特征提取和分类识别是人们在研究脑机接口系统时最关注的问题。

现有的P300 信号识别技术大部分是基于支持向量机[7－8]的，特征提取的方法主要有小波包分解[9]、独立分量分析[10]、主分量分析[11]以及小波变换[12]等。 传统“特征提取＋分类器”的框架将信号的特征提取和分类识别过程分离，增加了运算复杂度，降低了算法运行速度，但也舍弃了许多重要的特征信息。 卷积神经网络(Convolutional Neural Network，CNN)[13]是近些年发展起来的、一种非常高效的识别方法，可以直接在网络内部自动实现最优化的特征提取和分类，不需要人工选择脑电信号特征。 相比于传统的神经网络，CNN 不仅可以提取出更抽象、更具有区分度的特征信息，还能自发地从训练数据中学习已得到的特征模式，从而获得更好的识别效果。 例如，Cecotti[14]首次使用CNN 实现了对P300 信号的分类，获得了很好的字符识别准确率，证明了深度学习算法在脑电信号识别中的可行性。 Liu 等人[15]开发了一种新的卷积神经网络用于提高P300 拼写系统中的字符识别性能。 Li 等人[16]通过在简单贝叶斯卷积神经网络，有效地提高了网络对P300 信号的识别准确率。

本文在前人的基础上，改进了CNN 的网络结构，并根据P300 脑电信号的时频特性，选择经验模态分解(Empirical Mode Decomposition，EMD)算法和小波包分解(Wavelet Packet decomposition，WP)算法对原始脑电信号进行滤波处理，提出了一种基于EMD-WP 和卷积神经网络的P300 混合分类方法，记作T-CNN。 其中，EMD 算法用于将原始脑电信号分解为若干个本征模函数(Intrinsic Mode Function，IMF)分量，WP 算法用于对这些IMF 分量进行滤波处理，卷积神经网络用来自动提取重构信号的特征并进行分类。 本文在国际BCI 竞赛数据集上评估了所提出的基于EMD-WP 和卷积神经网络的P300 混合分类方法。 结果表明，该方法相比于传统算法显著提高了P300 信号的识别准确率。

1 方法

1.1 实验范式及数据预处理

本研究所用数据来自第三次国际BCI 竞赛所提供的P300 拼写器实验[17]。 实验中要求被试集中精力，注视图1(a)中由字母和数字组成的6x6 矩阵，并预先选择一个目标字符。 字符矩阵中所有的行和列随机闪烁100 ms(即该行或列的亮度加强)，每次闪烁间隔75 ms。 12个行列分别闪烁一次即为完成一次实验，周期为2.4 s。 每个字符进行15 次重复试验，然后进行下一个字符的测试。 当目标字符所在的行和列被加亮时，被试者需要在心中默记加亮的次数，其他行列被加亮时，被试者不需要做出反应。 这样，当加亮的行或列中包含目标字符时，便会诱发P300信号。 一次实验中，只有2个行列含有P300 信号，其余10个行列不包含P300 信号。 信号数据采集自64个电极，位置如图1(b)所示，采样频率为240 Hz 且经过0.1 Hz～60 Hz 的低通滤波器及信号放大器。 这样，每次刺激都会产生240×64 大小的样本数据。

图1 实验数据采集

有两名被试参与了本实验，编号分别为A、B，将他们产生的P300 电位数据分别处理成12×15×240×16×85 的五维张量，其中，12 表示字符矩阵每行(列)的编号，15 表示实验重复的次数，240 表示信号采样点数，16 表示选取的导联数目，85 表示目标字符数。本文选用枕叶区的16 导联数据进行研究，编号分别为32、34、36、41、9、11、13、42、47、49、51、53、55、56、60、62。 以被试A 为例，选取其产生的前55个字符数据作为训练集，后30个字符数据作为验证集，对原始数据作15 次叠加平均处理[18]。 其训练集和验证集包含的样本如表1 所示。

表1 每位受试者的训练集和验证集

1.2 实验原理

1.2.1 经验模态分解

EMD 算法是黄锷等人[19]在1998 年提出的一种自适应信号处理方法，它可以将一个复杂信号分解成若干个具有不同特征尺度的IMF 分量和残差信号。分解得到的IMF 分量有以下两个特征:①在整个数据范围内，极值点和过零点的数目相等或者差值至多为1；②在任意点处，由极大值点形成的包络线和由极小值点形成的包络线的平均值为零。

EMD 分解过程描述如下:

①找到信号x 的所有极值点，利用三次样条算法分别连接所有的极大值点、极小值点，得到两条上下包络线和Umin。

③检查得到的h1是否是固有模态函数，若是，则将h1作为第一个IMF 分量；否则将h1作为输入信号即x＝h1，重复步骤①～③。

④在得到一个IMF 分量后，将之前的输入信号变为x＝x－h1，并重复①～ ④步骤，直到Recall ＝变成一个单调函数信号。最终得到N个IMF 分量和一个残差序列。

1.2.2 小波包分解

小波包分解是对小波变换的延伸和推广，它可以对小波变换中没有细分的高频部分进行有效分解，并根据被分析信号的特征，自适应地选择相应频段，从而提高时频分辨率[20－21]。

小波包分解得到的是二叉树结构，将二叉树节点记为(j，i)，j是分解层数，i是该层节点个数，则信号在第j层第k个节点的小波包分解系数为:

经过小波包分解后，信号被划分为若干个频段，每个频段的频率区间为fs/2j＋1Hz，fs为采样频率。第j＋1 层第k个节点的小波包分解系数重构公式为:

1.2.3 改进的卷积神经网络

卷积神经网络是一种具有特殊拓扑结构的多层感知器，它具有独特的权值共享和局部感知特性，极大地简化了训练参数，降低了网络的复杂程度；同时能够充分利用信号本身所包含的局部特征。 CNN网络结构一般包括输入层、卷积层、下采样层、全连接层及输出层。 其中，卷积层用来提取信号特征，下采样层的主要作用是对输入的特征图降维，通常用在卷积层后面，全连接层的输入是CNN 的输出特征。

传统的卷积神经网络在识别脑电信号时不仅耗费时间长，而且分类的准确率也不尽人意[14]。 本文提出了一种改进的CNN 模型用于脑电信号的识别。该模型将卷积层中的卷积核设置为向量而非矩阵，使其只提取同一维度的特征，在保证分类准确率的基础上大幅减少程序运行时间，模型结构如图2所示。

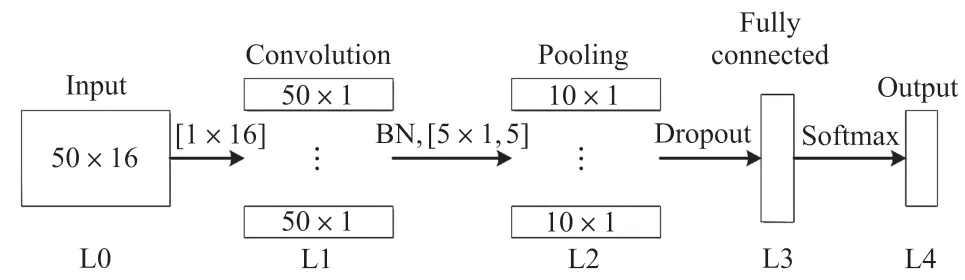
图2 改进的卷进神经网络结构

改进卷积神经网络结构由5 层构成。 具体描述如下:

第一层L0 是输入层，输入数据为经过处理后的P300 信号，每个输入样本的维度为50×16，其中50是每个通道中的采样点数，16 是选择的通道数；

第二层L1 是卷积层，在此层中对输入样本进行空间滤波和卷积运算。 卷积核数目设为20，大小为1×16。 使用ReLU 函数激活神经元，得到了20个特征映射图，大小为50×1。 在该层之后添加BN 技巧，对下采样层输入进行标准化；

第三层L2 是下采样层，主要作用是降低特征维度。 采用步长为5 的均值池化方法，每个神经元与卷积层中相应特征图的5×1 区域相连接，得到20个大小为10×1 的特征图；

第四层L3 是全连接层，该层引入了Dropout 操作，在训练过程中以0.6 的概率随机地关掉部分神经元，以防止CNN 模型过拟合。 全连接层将各个神经元节点的特征信号转换成向量信号，使用Softmax分类器判别输入样本的类别；

第五层L4 是输出层，因为本研究的目的是识别输入样本是否为P300 信号，所以最终有两种分类结果输出:‘1’表示P300 信号，‘0’表示非P300信号。

卷积网络的主要参数设置如表2 所示。

表2 CNN 的主要训练参数

表2 中MaxEpochs 表示最多遍历整个整个数据集50 次，MiniBatchSize 表示每次迭代时batch 块的最小尺寸为64，InitialLearnRate 表示初始学习率为0.001。

1.3 T-CNN 方法

脑电信号具有非线性、非平稳的特征，直接将原始脑电信号输入CNN 网络会带来比较大的误差。针对以上问题，本研究结合经验模态分解算法、小波包分解算法和卷积神经网络，提出了T-CNN 方法用于识别P300 信号。

该方法首先将P300 脑电信号进行EMD 分解，得到若干个IMF 分量，并根据脑电信号的有效频率范围，舍弃第一个IMF 分量；接着对剩余的IMF 分量分别进行小波包分解，保留0～30 Hz 范围内的信号成分；然后将经过WP 滤波后的各个IMF 分量进行叠加，得到重构后的脑电信号；又因为P300 信号出现在刺激发生后约300 ms，所以将选取0～625 ms内的数据进行下采样，采样因子为3。 最后，将处理好的数据送入改进的CNN 模型中进行训练和预测，以实现P300 脑电信号的识别。

T-CNN 方法的流程图如图3 所示。 图3 中，IMF1，IMF2，…，IMFn表示EMD 分解得到的n个固有模态函数，IMF′1，…，IMF′n表示经过小波包分解算法滤波后的固有模态函数。

图3 T-CNN 方法的流程图

1.4 评价标准

本文使用分类准确率对该方法识别P300 信号的能力进行评估。 分类准确率定义为正确分类的样本数与样本总数之比，计算公式为:

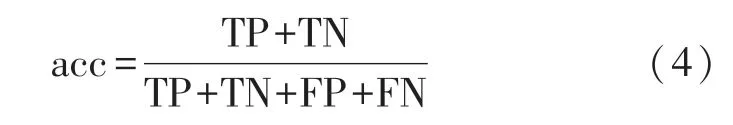
此外，还引入了如下指标评价P300 信号的识别结果，公式如下[22]:

Recall 表示召回率，Precision 表示精确率，F1-score 是识别率的延伸，结合了精确率和召回率。其中，TP 是分类为真实正例样本的数目，TN 是分类为真实负例样本的数目，FP 是错分为正例样本数目，FN 是错分为负例样本的数目。

2 结果分析与讨论

本文在MATLAB R2018a 平台上对训练集和验证集进行仿真实验，使用6 折交叉验证的平均结果以验证T-CNN 方法在P300 信号检测中的有效性。实验中使用rng()函数控制随机数的生成，设置其种子数为3，使得CNN 模型每次初始化参数时使用的随机数保持一致。

2.1 P300 信号的滤波与重构

为便于观察，本研究随机选取了被试A 在Cz通道内的一组P300 数据。 首先使用EMD 算法对P300 信号进行分解，得到5个固有模态函数，如图4所示。 每个IMF 分量对应着不同的频率成分，且不同的IMF 分量之间波形差异明显，幅度也不同。

图4 P300 信号的EMD 分解

再对每个IMF 分量进行频谱分析，画出对应的频谱图如图5 所示。 可以看出第一个IMF 分量的频率成分主要集中在40 Hz～80 Hz，而P300 信号的频率范围为0～30 Hz。 因此本文舍弃了第一个IMF分量，采用IMF2～IMF5这四个IMF 分量分别进行4层小波包分解，并以db4 小波作为小波基函数。 脑电信号的采样频率为240 Hz，由抽样定理知，奈奎斯特频率为120 Hz。 分解了4 层，最后一层有16个频率段，则每个频段的范围是120/32 ＝7.5 Hz。 根据P300 信号的有效频段和公式(3)，选择第四层的前4个小波包子带重构脑电信号。 表3 给出了这4个子带的频率范围。

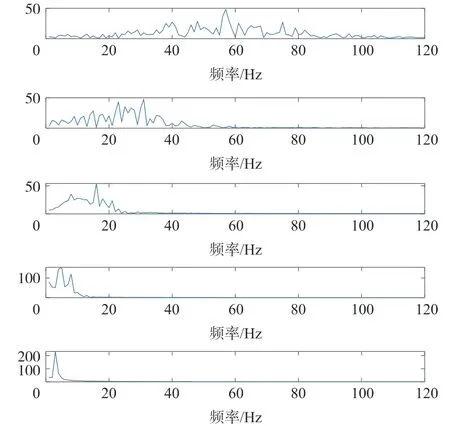
图5 IMF 分量对应的频谱图

表3 前4个小波包子带对应的频率范围

将经过小波包分解后的各个IMF 分量叠加，重构P300 信号。 原始P300 信号与重构P300 信号的比较如图6 所示:通过2个信号的波形可以看出重构的P300 信号保留了原始信号的大部分特征，为了定量分析该方法的消噪效果，本文将去除的IMF1 分量作为噪声信号，并且使用信噪比作为评价标准。 经过计算，原始信号和重构信号的信噪比分别为2.07、6.82，说明重构信号消除了大量的随机噪声，EMD 算法和WP 算法的滤波效果是较为理想的。

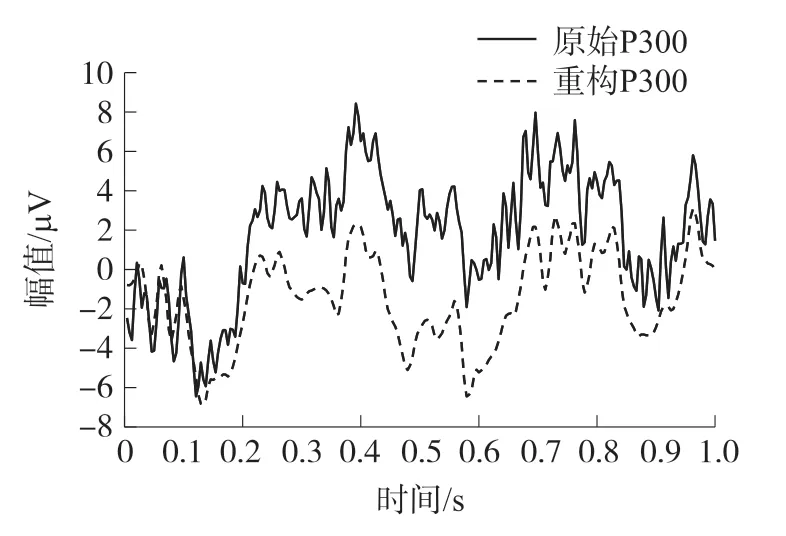
图6 原始P300 信号与重构P300 信号

2.2 T-CNN 方法对P300 信号识别结果

同样以受试者A 为例，将其训练集输入改进的卷积神经网络，训练准确率和损失函数曲线如图7所示，横坐标均表示迭代次数，纵坐标分别表示准确率和损失值。 训练过程中遍历数据集50 次，每次进行10 次迭代，每次迭代时batch 块的最小尺寸为64，总共进行了500 次迭代。 从图7 中可以看出，在迭代次数多于400 次以后，训练准确率和损失值基本稳定，两条曲线均趋于收敛。 可以认为网络在第400 次时达到最好的训练效果，此时训练准确率为98.44%，损失值为0.071 5。

图7 CNN 训练过程中的训练准确率曲线和loss 曲线

使用验证集检验训练好的模型，P300 信号的分类准确率为97.78%，证明了T-CNN 方法在P300 信号识别中的有效性。 被试A 在该模型下的召回率、精确率和F1-score 如表4 所示。

表4 P300 信号分类结果的召回率、精确率和F1-score

和文献[15]相比，该方法得到了更高的召回率、精确率和F1-score，这意味着更好的分类表现。

为了更加客观地评价本文提出的方法，本文将T-CNN 方法与其他P300 识别方法进行了比较，如图8 所示。 支持向量机(Support Vector Machine，SVM)、线性差别分析(Linear Discriminant Analysis，LDA)和T-CNN 三种方法使用的输入数据均经过EMD 算法和WP 算法处理，而tT-CNN 使用的输入数据未经过WP 算法处理。 使用tT-CNN 方法和TCNN 方法分别对两名受试者产生的P300 数据进行识别，得到的分类准确率均比传统的支持向量机、线性判别分析方法要高，说明使用深度学习算法确实能够更好地对P300 脑电信号进行分类。 而两名受试者使用tT-CNN 方法得到的分类准确率分别为95%、94.17%，使用T-CNN 方法得到的分类准确率分别为97.78%、95.56%，说明相比于对只经过消噪的P300 数据进行分类的tT-CNN 方法，T-CNN 方法获得了更高的分类准确率。

图8 多种方法识别效果对比

2.3 讨论

针对P300 脑电信号非线性、非平稳的特性，本研究使用EMD 算法和WP 算法对信号进行滤波(图4～图6)。 实验结果表明(图8)，与直接将信号送入改进的CNN 模型相比，使用WP 算法进行滤波使得两名被试的分类准确率分别提高了2.78%、1.39%。 这说明同时使用小波包分解算法与改进的卷积神经网络模型对P300 脑电信号进行二级特征提取与分类，能够有效地改善信号的识别效果，获得更高的分类准确率。 这表明通过EMD 得到的有效IMF 分量能准确分类P300 信号。 同时可以看到，相同算法在不同受试者产生的P300 数据上的分类表现存在差异，这进一步验证了P300 脑电信号的个体差异性，提醒我们需要开发出一种具有普适性的脑电信号分类算法。 而在只使用EMD 或WP 算法的情况下，以受试者A 为例，P300 信号的分类准确率分别为91.25%、93.75%，均比同时使用时的准确率低。 这表明EMD 和WP 算法的组合有效地过滤了信号中的噪声，同时也对信号中的特征进行了简单提取，方便了后续卷积神经网络对信号的分类。

脑电信号是一种具有时间特性和空间特性的信号，为了保证卷积运算后的特征中不会同时包含空间和时间信息，本研究对传统的卷积神经网络进行了改进，如图2 所示。 在设计CNN 网络结构时，本文只使用了一个卷积层。 卷积核设置为向量而非矩阵，保证了卷积层只能提取空间特征或时间特征。实验结果如图8 所示，改进的CNN 网络模型，相比于普通的分类器能够有效地改善P300 信号的识别准确率。 在实验过程中，为了得到分类效果较好的CNN 模型，本文研究了不同参数设置的网络。 结果表明，在样本确定的情况下，模型的分类准确率和网络的复杂度并没有必然的联系。 针对训练过程中可能出现的过拟合现象，我们在CNN 网络结构中添加了BN 和Dropout 技巧，在防止过拟合的同时还提高了识别准确率。

本研究的主要工作是对P300 脑电信号进行处理和分类，是在离线环境下进行的。 因此，虽然本文提出的方法有效改善了P300 信号的识别准确率，但要想开发出可以实时处理信号的在线BCI 系统，仍有很多问题需要解决。 由于目前在设置CNN 网络参数时，主要还是依靠研究者的经验及多次重复实验，随机性太大且缺乏理论依据，所以如何选择合适的算法来确定CNN 网络的参数将是笔者后续的研究内容。 而少量的受试者更是无法从统计学意义上说明本文提出方法的有效性，使用更多的数据集去验证该方法也是必要的工作。

3 结论

本文通过对P300 脑电信号的研究，提出了一种将经验模态分解、小波包分解与改进的卷积神经网络相结合的方法，实验结果表明，该方法能够有效地提高P300 信号的识别准确率，为基于P300 信号的脑机接口系统实现提供了一条新思路。