回声状态网络在气候预测方面的应用研究

王人杰 刘海忠＊ 朱 洋

（兰州交通大学，甘肃 兰州 730070）

21 世纪，经济的发展速度比以往任何时候都要快。但工业文明的过快扩张也促使我们生存的环境受到了极大的破坏，最为典型的问题就是全球变暖。这是一个全球范围内的严重问题，每一个国家和地区都无法置身事外[1]。

1 研究现状

Zhang 等学者[2]在前人研究成果的基础上创新性地提出了SCAD 罚函数模型，能够把样本当中的小变量设置为0，从而更好地反映出变量稀疏性，同时设置大变量为常数以解决过拟合，使最终的结果符合无偏估计。在处理多维且复杂的气象数据时效果良好，但SCAD 的本身方程中涵盖了过多需要调整的超参数的值，大大的增加了计算量，尽管也有人试图采用粒子群算法(PSO)对超参数进行联合估计，但计算仍然复杂繁琐，而且粒子群算法本身也存在着一些不足[3]，如：算法容易陷入局部最优解[4]，后期收敛速度慢，导致算法求解精度不高。谢倩[5]采集了近年来岭南地区的气候变化数据，围绕着广州周边的数据样本来进行量化分析，从人体热感觉、风向以及日轨等多个不同的维度来梳理总结出气候变化所表现出的特征，最终总结出气候变化的规律。这样通过数据的表示使气候的特征更为直观，但该研究的问题在于，考虑的变量并不全面，忽略了一些影响可能相对显著的因素。

本文选择以PCA-ESN 的气候预测模型来进行样本分析。第一步，先对采集的数据进行预处理，然后以主成分分析方法(PCA)提取样本数据的主要特征，减少数据中的冗余信息。第二步，以ESN 方法构建气候预测模型，有效地解决传统方法极易出现的梯度消失等问题，该模型在实际的应用过程中表现出十分优异的信息处理能力。

2 数据简介及预处理

2.1 数据简介

原始数据为广东省广州市黄埔区1980 年1 月1 日至2020 年12 月31 日的气象日数据，共14976 组。本次研究采集的数据包括当地的平均地表气温、当日最高与最低地表气温、最大风速、各个时间段的降雨量、当地最高与最低气温、平均气压、平均相对湿度等指标。

2.2 数据预处理

数据样本的预处理会直接影响数据分析结果的准确性和真实性[6]。在多元统计分析中，主成分分析法能够从数据样本当中有效提出变量特征，降低数据的冗余度，为之后数据模型的应用和预测奠定良好的基础。此外，主成分分析法还能解决信息重叠所带来的负面影响，提高分析结果的准确度[7]。

设原始数据集包括n 个数据样本，每个样本具有p个变量，将数据在SPSS 软件中进行主成分分析，得到成分矩阵如表1 所示[8]：

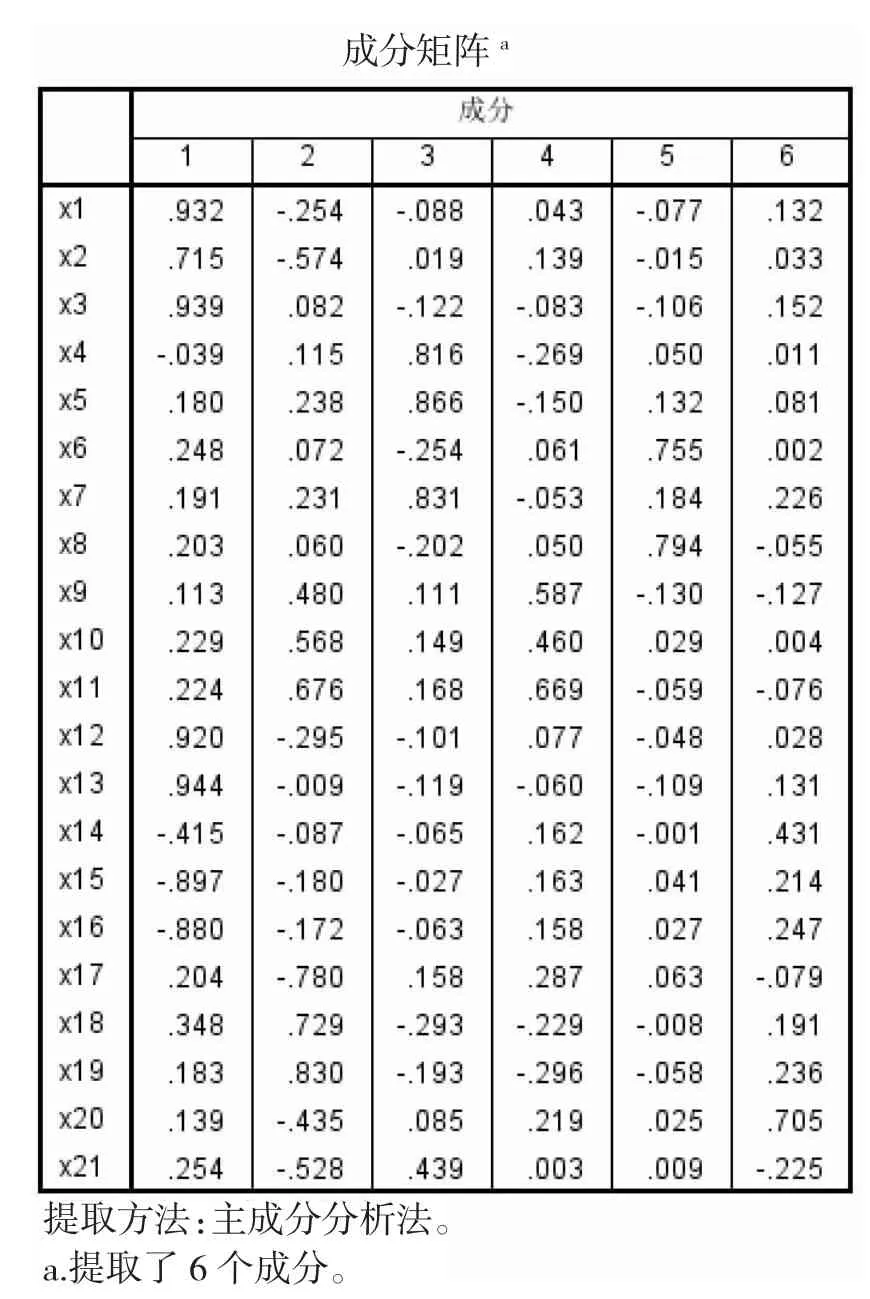
表1 成分矩阵

根据上表1 的对应数据，可以得到经过标准化之后的6 个主成分因子表达式，以第一个主成分为例，计算过程为：首先从表1 成分矩阵中，计算第一列数据的平方和，即0.9322+0.7152+…+0.2542，根据主成分分析的定义，该平方和被称为“第一主成分的方差”。将该方差的平方根除成分矩阵第一列的每个元素，即0.932/√(主成分方差), 0.715/√(主成分方差), …, 0.254/√(主成分方差)，便得到第一个主成分的各个系数0.370694, 0.28453, …,0.100956。

3 模型和算法

3.1 主要模型

本次研究选择使用的ESN 模型属于储备池计算网络范畴[9]，表现出鲜明的动力学特征。从结构上来看，ESN可以分为3 层，分别是输入层、输出层以及储备层。在储备层中，ESN 包含了大量的神经元，以随机的方式进行连接，具有储备短期记忆的功能。在整个网络中，储备池是最重要的核心部分，也关乎网络的运行性能，内部结构可参考图1。

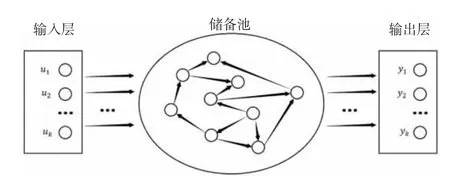
图1 ESN 结构图

设输入矩阵、状态矩阵、输出矩阵分别为：

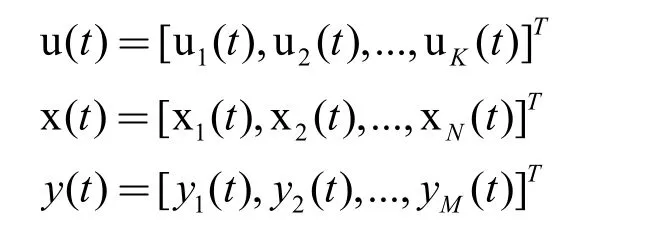
其中，K 为输入维数，N 为储备池内部神经元个数，M 为输出维数，T=1，2，……，T。

状态矩阵的更新如下式所示：

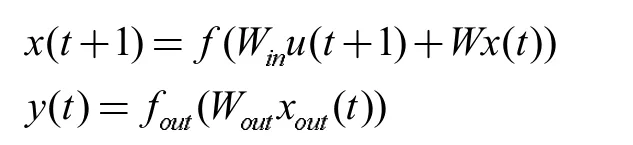
其中，Win是输入层到储备层的N×K 的权重矩阵，W 是储备层权重矩阵，Wout是储备层到输出层的M×K的权重矩阵，此矩阵的更新如下式所示：

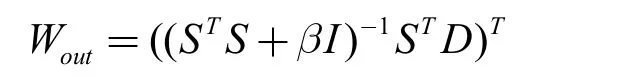
其中，β 表示非负正则化系数，S 表示全部状态矩阵，I 表示单位矩阵，D 为全部输出矩阵。

3.2 训练算法

ESN 模型训练过程如图2 所示。

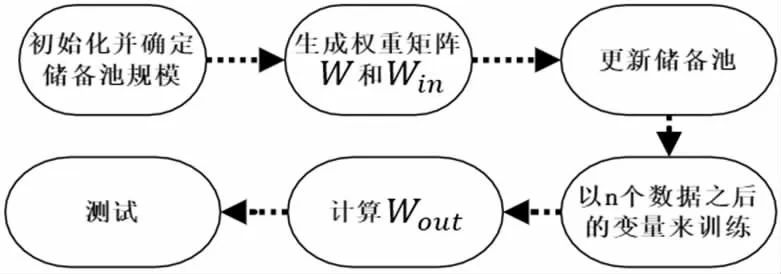
图2 ESN 训练过程示意图

第一步，进行初始化操作，先确定储备池的规模，即神经元的个数。

第二步，随机生成两个矩阵，分别是输入层和储备层的权重矩阵，并通过缩放因子大小的调整，确保谱半径位于[0,1]的范围内。

第三步，样本数据依次加载到输入、输出，更新储备池内部状态。

第四步，删除x（1）至x（n）的数据，这个数据并不涉及模型训练，但却都会不同程度地受到初始瞬变影响，并训练该n 个数据之后的变量。

第五步，计算输出权重矩阵Wout。

第六步，用新输入和训练好的Wout计算相应输出，进行测试。

4 实验

本次研究先将所有的样本数据（14976 组）进行归一化处理，接着通过PCA 算法来获取新主成分。之后，以样本中11980 组数据作为模型训练，后面的数据用作模型测试。将ESN 模型的各项参数设置为：节点数为2；神经元稀疏度为5%；储备池中含有神经元总数为50，输出节点数为1。

以调参后的ESN 模型作为气温预测的系统，当模型反复运行30 次后，最终的结果逐步稳定，可以作为模拟结果，具体测试效果可参考图3。

图3 ESN 预测效果图

将预测结果和原数据放在同一张表格中，这里决定选取绝对预测误差率APE 对预测输出的结果的偏离程度进行整体分析，计算公式如下：

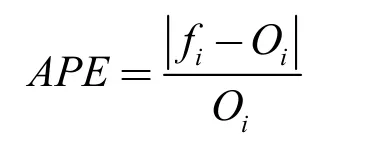
其中，fi表示第i 次的预测值，Oi表示相对应的实际值。误差测试图如图4 所示。

从图4 可看出，预测误差率全部介于(0,1)内，且大多数预测误差都在15%以下，极少部分计算值存在着较大偏离，不具备参考价值。由此可知，ESN 的测试输出能够很好的拟合真实的气温数据，预测效果良好。

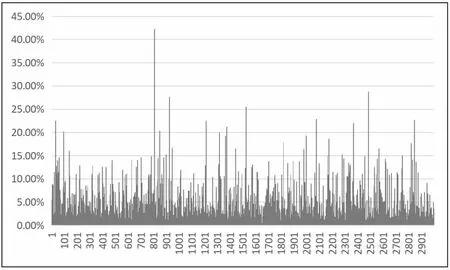
图4 误差测试图

继续选用ARIMA 模型[10]和LSTM 模型对原始数据进行预测，并计算ESN 模型、ARIMA 模型和LSTM 模型的预测结果的均方误差(MSE)，MSE 的计算公式为[11]：

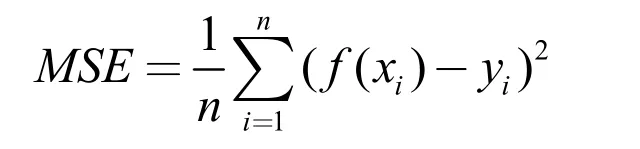
结果详情可见表2。

表2 三种预测模型的均方误差比较

由表2 可知，ESN 的均方误差是最小的，在量级上远小于另外两个模型。由此也可以进一步显示出ESN 预测模型在预测方面的优越性。

5 结论

本文以广州市黄埔区的气象数据作为研究对象，将主成分分析法和回声状态网络相结合，提出了基于PCA的ESN 模型进行气候预测，总结如下：

我们利用了主成分分析法本身的特性，使得本文模型可以有效处理规模庞大的数据集，避免迭代次数过多。本研究以PCA 算法来对原始气候数据展开预处理，并获得6 个主成分。以这6 个主成分作为模拟预测的输入变量，在此基础上建立ESN 预测模型，反复运行后可以预测当地的气温，有效地降低了样本数据的计算复杂度。由于本文所研究的数据集具有非线性、季节性等特征，常用预测模型在面对这样类型的数据时，往往要经过十分繁琐和复杂的数据处理和运算阶段，但ESN 模型在预测这样的时间序列数据时具有更为良好的性能。实验结果表明，利用ESN 模型预测经过PCA 处理之后的气候数据，预测值和实际值的总体偏差小，均保持在较低水平，绝对预测误差普遍处于15%以下，预测效果优于LSTM 模型和ARIMA 模型。因此，本次研究构建的PCA-ESN 模型能够被应用到气候预测中，为今后的气候数据分析提供了重要的参考。