基于改进粒子滤波算法的水下地形辅助导航方法

陈睿玮，车驰东

（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

对于海洋资源的探索一直以来都受到世界各国的高度重视，尤其在极地区域，蕴含着丰富的自然与航运资源，利用水下航行器（Autonomous Under-water Vehicle，AUV）在极区进行水下环境与海洋物理等信息的采集成为了海洋资源开发的重要一环。AUV的工作效率与工作质量与其导航的性能高度相关，但受水下环境的制约。如全球定位系统（Global Positioning System，GPS）、基线定位法等传统的高精度定位方法在AUV水下作业时无法使用，在有冰层常年覆盖的极区，AUV无法浮出水面接收GPS信号修正定位，且基线定位方法所需的外部辅助设备在极地冰雪层上施工困难。AUV只能通过惯性导航提供短距离内的定位，传感器的漂移导致误差随AUV航行时间的增加而累积。

高精度的自主导航问题可以通过使用水下地形辅助导航（Terrain Aided Navigation，TAN）技术解决。TAN方法通过将采集到的地形与地图信息进行匹配，推算出当前测点的位置。TAN方法根据匹配形式可以分为地形轮廓匹配（Terrain Contour Matching，TERCOM）和递归贝叶斯估计。TERCOM技术是一种批相关处理的方法，早期用于飞行器和导弹制导，现在技术已经较成熟，并有广泛的应用，但由于其实时性较差及无法处理过程和量测噪声，用于AUV导航的效果并不理想。基于递归贝叶斯估计的导航方法可以有效地处理过程噪声，其中具有代表性的有卡尔曼滤波（Kalman Filter，KF）、扩展卡尔曼滤波（Extended Kalman Filter，EKF）和无迹卡尔曼滤波（Unsented Kalman Filter，UKF）。EKF和UKF虽然解决了KF无法用于非线性系统的问题，但二者仍要求系统的观测是高斯分布的，具有局限性。粒子滤波（Particle Filtering，PF）利用随机分布的粒子逼近后验分布，解决了KF及其衍生方法的问题，成为当前TAN技术研究的主流方向。

PF方法为了解决粒子权值过低而产生粒子退化的问题，引入了重采样步骤，但重采样导致高权值粒子被大量复制，使粒子的多样性匮乏，即产生粒子贫化现象。现有研究的主要目标是在剔除低权值粒子的同时，保持粒子的多样性。近年来，研究人员通过将相关系数、高斯和滤波器等引入PF算法，使粒子贫化问题得到改善，并应用于水下地形辅助导航中。研究表明，PF方法用于AUV的长航程、高深度工作也具有良好的性能。

学者们也对TAN的鲁棒方法做了大量研究。当前的导航鲁棒方法可概括为2种：提高局部定位自适应能力，直接提高局部定位精度；提高逃离局部最优定位的能力，间接提高全局定位鲁棒性。现有TAN方法的研究多基于高分辨率的海底地图，文献[23]的数据表明，导航的精度在分辨率较低时与其呈正相关。当前对极地区域开发仍处于起步阶段，现有的水下信息并不充分。目前北极地区的海底地形图分辨率仅为500 m，且具有分辨率低、噪声大、特征稀疏、平坦区域面积大等特点，这些不利因素使得现有的TAN方法作用于低分辨率海图时，在精度和鲁棒性上都表现较差。文献[25]提出了一种带粒子抖动的粒子滤波（Jittered Bootsrap Particle Filter，JBPF），通过给重采样后的粒子添加额外噪声，来改善粒子贫化，该方法在基于分辨率为500 m的海底地形图导航仿真中得到较低的导航误差。JBPF添加的粒子抖动在抖动半径较大时，将引入较大的额外误差；而半径较小时，则鲁棒性下降。

本文针对低分辨率海底地形图的水下地形辅助导航，提出一种带有自抖动及修正的粒子滤波方法（Self-jitter and Correction Particle Filter，SJCPF）。通过在重采样步骤中根据相关系数对粒子权值进行调整，并引入额外噪声，增加粒子的多样性，在保证鲁棒性的基础上，增加了导航精度，且提高了算法的效率。

1 粒子滤波及改进方法

1.1 基本理论

粒子滤波的本质是一种贝叶斯估计，采用蒙特卡洛方法，通过随机生成的粒子来近似概率分布。基于传统的粒子滤波的辅助导航算法包含以下几个步骤。

1）起始位置的粒子初始化：在起点处附近以一定的概率分布（如均匀分布、高斯分布等）生成一组离散点，每一个点代表在初始时刻AUV可能存在的位置，此时每个粒子的权值相等。

2）粒子位置更新与预测值、测量值获取：从惯导系统获取数据，并推算AUV在2次测量中的位移量，更新所有粒子的位置，并根据新的粒子位置在数字地图上获取深度的预测值，测量值可由测深传感器得到。

3）粒子权值更新及重采样：根据测量值和预测值更新每个粒子的权值，将得到的权值归一化后，重新从粒子中采样，得到新的一组权值一致的粒子。

4）航行位置预测值更新：将粒子的位置加权平均后得到AUV航行位置的预测值。

导航过程中，迭代步骤2—4），算法将连续地提供AUV的预测航迹。

1.2 粒子抖动

虽然重采样的引入改善了粒子退化的现象，但是随着迭代次数的增加，保留的大量高权值粒子只集中在几个很小的区域内，尤其在低分辨率海图的条件下，地形信息的相对匮乏，对数字海图插值带来的误差更大，传统算法的重采样步骤将过早地舍弃部分低权值但接近AUV实际位置的粒子。为了解决上述问题，引入粒子抖动，即在每次粒子位置更新时，引入额外的过程噪声，该过程噪声采用高斯分布。该方法使得传统算法中过度集中的粒子适当向周围发散，改善了算法本身及海图分辨率低带来的粒子多样性匮乏。

1.3 相关系数修正重采样权值

在算法中采用粒子抖动，一方面解决了粒子贫化的问题，改善了算法的鲁棒性，但同时也引入了额外的过程误差。考虑到AUV航速较慢，并且在长航程工作时采样频率低，可以在算法中引入TERCOM方法批相关处理的思想。根据每个粒子前几次的预测值序列与测量值序列，得到其对应的相关系数ρ，重采样时使用该系数修正粒子的权值ω。

在统计学上常用的相关系数有皮尔逊相关系数（Pearson Correlation Coefficient，PCC）、斯皮尔曼秩相关系数（Spearman's Rank Correlation Coefficient，SRCC）及肯达尔秩相关系数（Kendall Rank Correlation Coefficient，KRCC）。PCC是一种线性相关系数，通过2个变量、的协方差除以它们的标准差乘积得到，变量的序列长度为。

PCC本质上是2组变量协方差的归一化，取值范围为–1~1，其计算的时间复杂度为()。SRCC和KRCC都是秩相关系数，其中SRCC可以理解为对数据排序后并用排序位置代替原始数据得到的PCC。

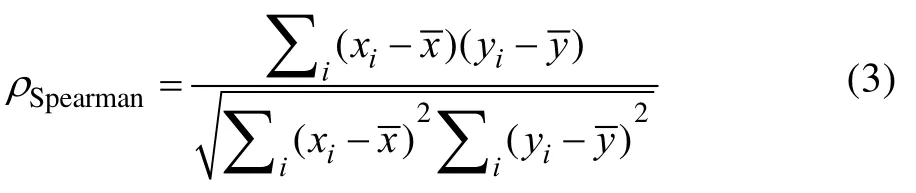
式中：x、y为X、Y对应的排序位置数据。由于使用了排序，SRCC的时间复杂度为(lg)。

KRCC通过数据对(X,Y)、(X,Y)的两两比较得到。

式中：为满足X>X且Y>Y或X<X且Y<Y的数据对组数；为不满足前述条件的组数。由于计算过程需要对每2组数据分别比较，KRCC的时间复杂度为()。

1.4 带有自抖动及修正的粒子滤波方法

基于上述讨论并针对AUV的航行特点，本文提出了一种基于SJCPF的水下地形辅助导航算法。该算法的计算步骤如图1所示。

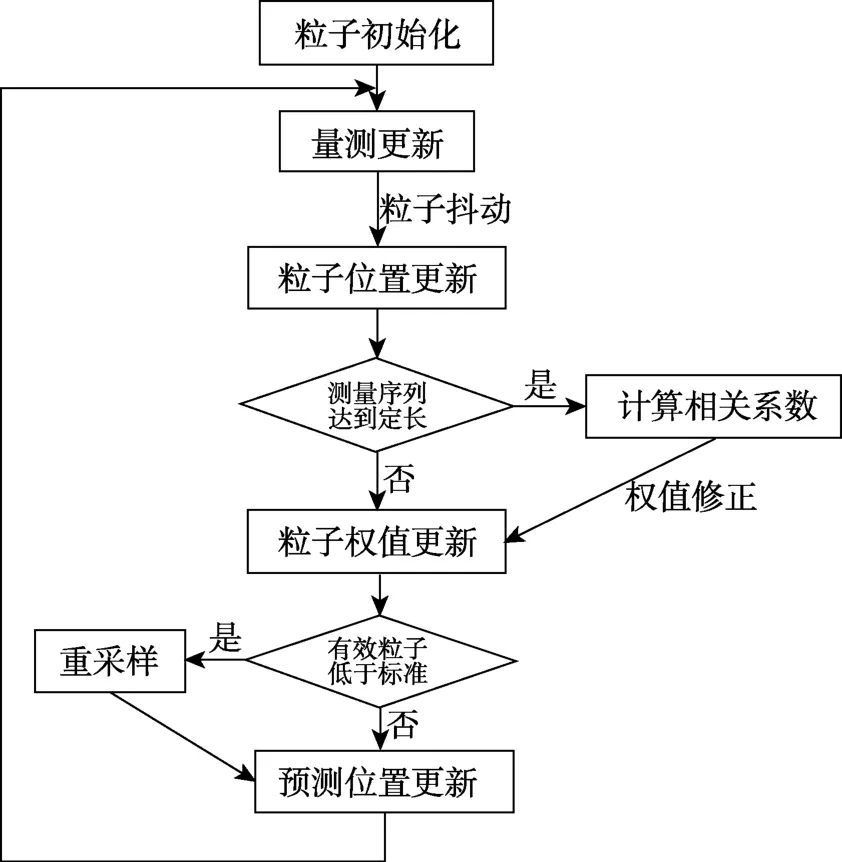
图1 SJCPF算法流程 Fig.1 SJCPF algorithm flow chart

1）粒子初始化：在起始点的位置附近，采用高斯分布对粒子的位置进行初始化。

2）粒子位置更新及抖动：在每个测量区间，根据惯性系统的数据，更新粒子的位置，并为更新后的粒子位置添加高斯噪声。

3）相关系数修正粒子权值及重采样：当测量值及预测值序列长度达到设定的最低值后，计算2组变量的相关系数，并将其用作核函数的参数修正粒子权值，采用修正后的权值对粒子进行重采样。

4）位置更新：将粒子的位置加权平均后得到AUV航行位置的预测值。

2 仿真与分析

对传统PF算法及SJCPF算法的导航性能进行仿真，选用北纬75.27°~75.6°、西经162.5°~161°区域的数字海底地形图，地图分辨率为500 m。SJCPF算法中，粒子的抖动方差取225 m，重采样的相关系数采用Pearson相关系数，核函数取指数函数。以75.27°N、162.5°W为坐标原点，仿真中AUV按以上参数沿规定航迹行驶，起始位置为北向1 000 m，东向15 000 m。假设起始位置不存在误差，2种算法的航迹图及误差随位移的变化曲线如图2及图3所示。

由图2和图3可以看出，PF算法在预测位置偏离航迹后，并没有及时有效地调整，在航迹图中的表现近似于静差，其导航误差也维持在500 m以上。这直接体现了传统PF算法的粒子贫化问题。由于导航 过程中粒子逐渐集中在高权值粒子附近，在出现较大的导航误差时，真实位置附近可能不存在粒子，误差难以消除。

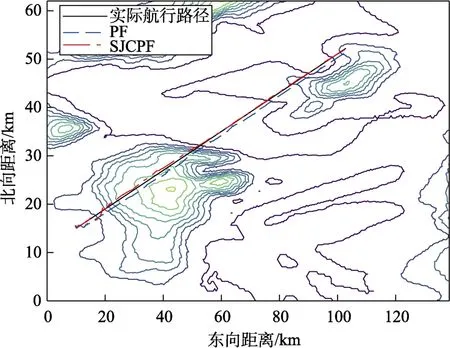
图2 PF算法及SJCPF算法的地形匹配结果 Fig.2 Terrain matching results of PF and SJCPF

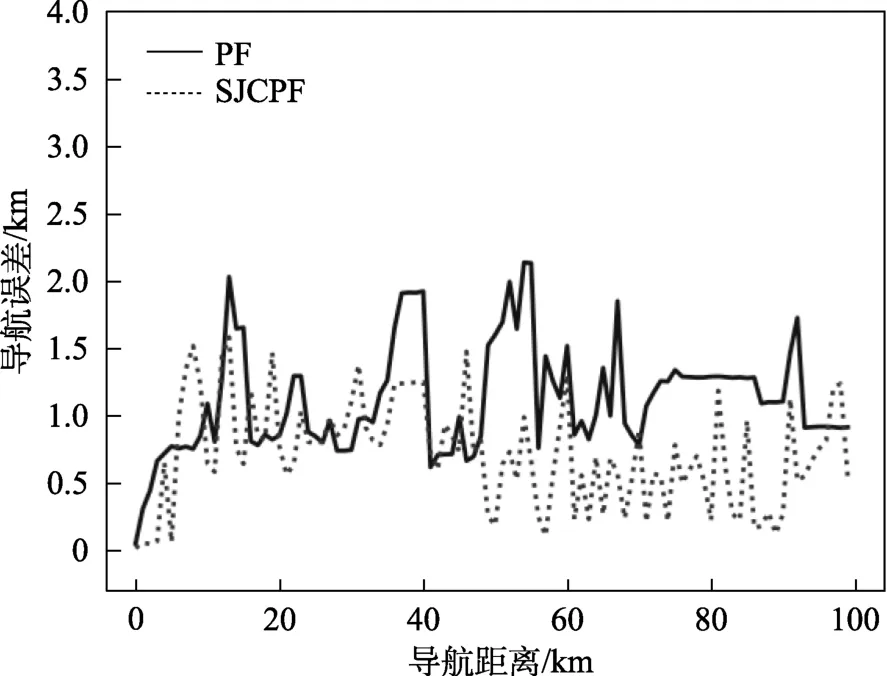
图3 PF算法及SJCPF算法的匹配结果 Fig.3 Matching results of PF and SJCPF

SJCPF算法的预测航迹与实际航迹的重合度更高，导航误差的均值也显著低于传统PF算法。这是由于SJCPF引入的过程噪声以及在重采样过程中保留了更多的粒子，并放大了相关系数高的粒子的权值，在导航误差较大的时候也能及时调整至真实位置附近。

对以上仿真进行200次重复性试验后，得到传统PF算法和SJCPF算法的均方根误差分别为1 767.75 m及1 277.31 m，SJCPF算法控制导航误差的能力显著优于传统PF算法。

在表1参数的基础上，通过控制SJCPF算法的部分参数，研究算法对导航精度的影响因素。改变重采样中相关系数的求取方法，分别为PCC、SRCC、KRCC。由图4可以看出，基于KRCC的SJCPF算法的导航误差相对较小，极值也更低，但与PCC及SRCC并未有明显区别。对该仿真进行200次重复性试验，基于SRCC和KRCC导航算法的均方根误差分别为1 386.98 m及1 241.01 m，相较于基于PCC的1 277.31 m没有明显提升。在算法耗时上，基于PCC的算法执行单次循环体需140.59 ms，SRCC为301.19 ms，KRCC为235.37 ms，并且随着粒子数量增加，计算SRCC和KRCC耗时的增速要显著大于计算PCC的耗时。因此，综合考虑导航性能，选用PCC更优。

表1 仿真参数 Tab.1 Parameters of Simulation

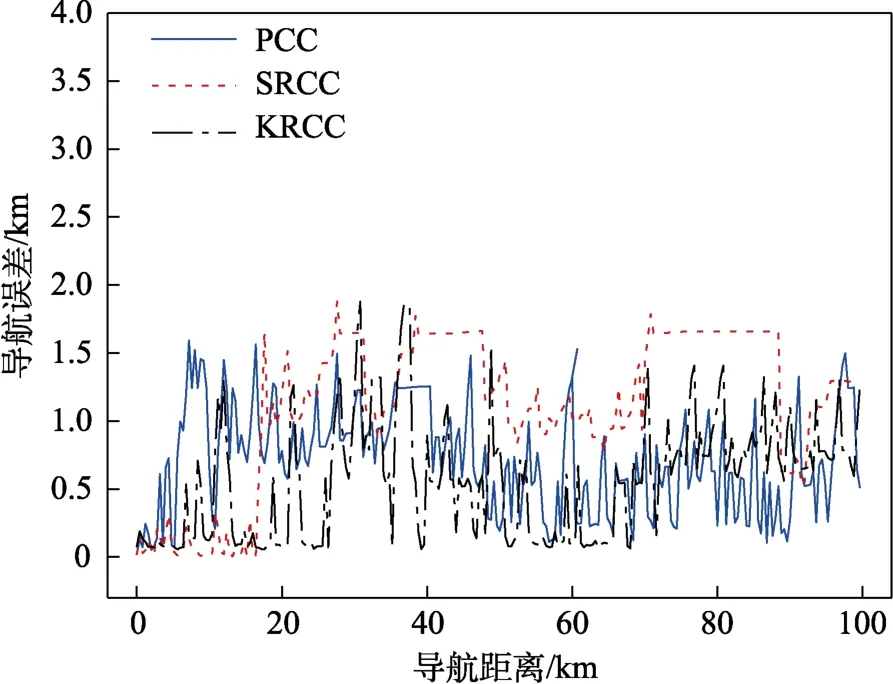
图4 SJCPF算法基于不同相关系数的匹配结果 Fig.4 Terrain matching results of SJCPF based on different correlation coefficients

改变SJCPF算法中粒子的数量，分别取50、500、1 000。从图5中可以看出，随着粒子数量的增加，导航的精度及稳定性都有所提高。但当粒子数量较大时，这一提升便开始减小，并且粒子数量的增多将增加计算负担，给功耗和耗时都带来负面影响。在粒子数量只有50时，由于粒子数量过低，放大了引入的过程噪声带来的影响，导航稳定性大大降低；粒子数量提升至1 000时，由于粒子密度已经较高，对导航精度的提升有限。

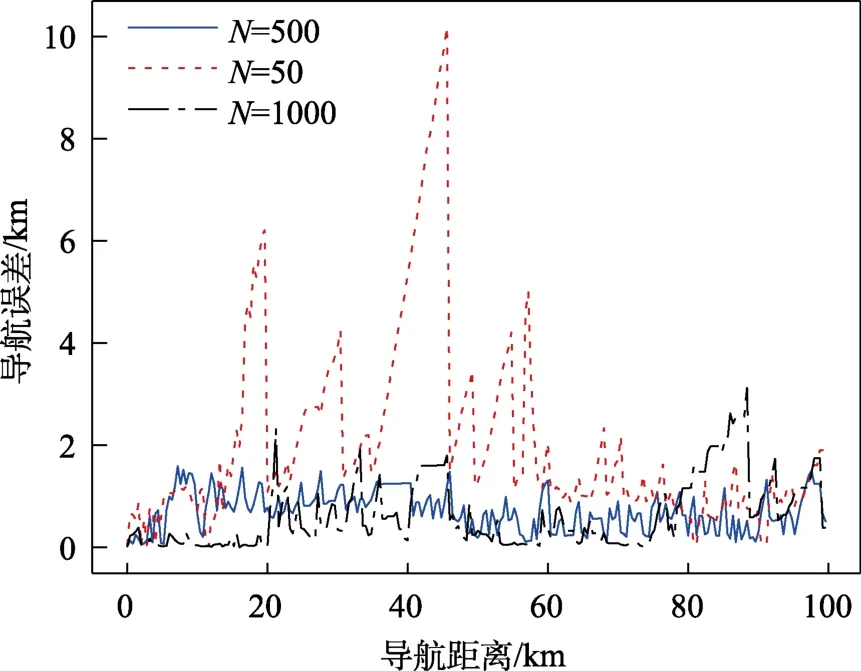
图5 SJCPF算法基于不同粒子数量的匹配结果 Fig.5 Terrain matching results of SJCPF based on different number of particles

改变SJCPF算法中的测量频率，分别取0.05、0.01、0.001 Hz。随着测量频率的提升，导航误差的均值及方差都有明显的降低，如图6所示。这一结果表明，工程中需要避免使用过低的测量频率，但并不意味着需要大幅提升测量频率。一方面，更加频繁地使用测深仪器会增大AUV的功耗，降低其续航能力；另一方面，仿真所使用的插值地图并不能很好地模拟网格节点间的真实地形，实际上这部分的误差并不能通过提高测量频率来消除。因此，综合考虑，只需要选用能使测量间距略低于网格分辨率的测量频率即可。

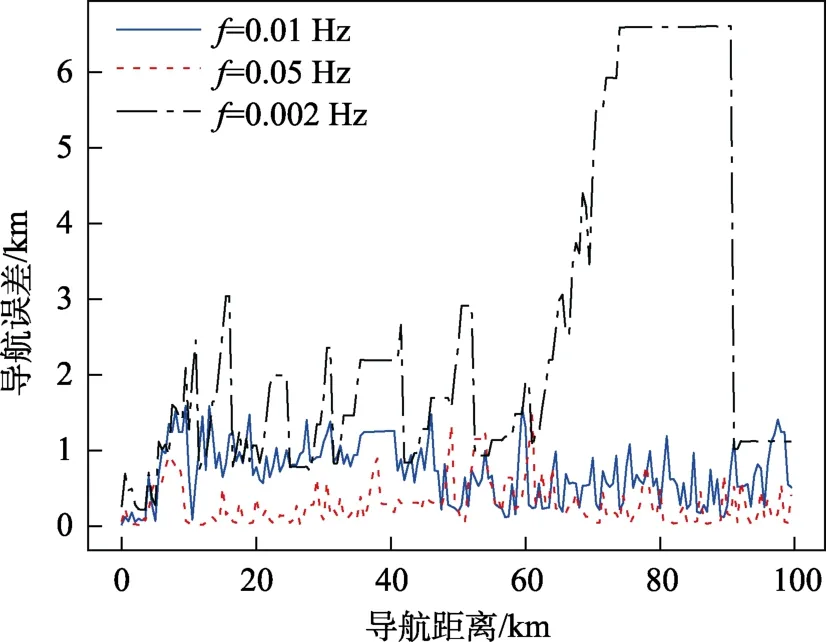
图6 SJCPF算法基于不同测量频率的匹配结果 Fig.6 Terrain matching results of SJCPF based on differ-ent measuring frequency

3 结论

1）SJCPF算法较好地解决了传统PF算法的粒子贫化问题。在低分辨率海图的条件下，粒子贫化所带来的误差影响尤为明显，传统PF算法极易在误差较大时脱离原航迹，产生导航静差。SJCPF算法增加的过程噪声使得误差较大时粒子仍有机会回到真实位置附近，并且运用粒子先前时刻测量值求取的相关系数修正权值，避免了部分贴近真实航迹的粒子只因为一次测量值偏差较大而被剔除，增加了算法的鲁棒性。相较于传统PF算法，导航的均方根误差降低了27.7%。

2）通过比较不同参数对SJCPF算法导航性能的影响，发现PCC、SRCC、KRCC这3种相关系数用于算法中都可以得到较低的导航误差，其中KRCC表现最佳，但是提升程度有限。在耗时方面，PCC由于拥有线性的时间复杂度而远低于SRCC和KRCC。导航误差和粒子数量呈负相关，在粒子数量较小的时候，粒子数量的提升对导航误差的控制效果显著；粒子密度较高时，粒子数量增加并不能明显降低误差，反而增加了算法耗时。测量频率对导航误差的影响与粒子数量类似，在频率较低时提升明显，频率较高时提升测量频率对导航误差的影响有限，且受制于仿真使用的地图精度，高测量频率带来的误差减小可能只适用于仿真中，而无法在实际工程中实现。因此，在实际工程中，使用SJCPF算法进行水下地形辅助导航时，可选用PCC作为相关系数，使用较高的粒子数量及较高的测量频率，可以兼顾AUV的续航及导航精度。