典型仪器支架动力学管控方法研究

李雨青，邵旭东，李炳蔚

（中国运载火箭技术研究院，北京 100076）

随着高速飞行器技术的发展，飞行器在极高飞行速度和大动压条件下，往往会造成较高量级的飞行气动噪声和形成飞行振动环境，这带来了严重的力学环境问题。高量级的振动环境会引起设备失效和结构破坏，成为飞行器设计必须考虑的重要因素之一。为了避免飞行器的关键设备、结构在飞行条件下失效，一方面，在单机设计中需要提高设备的环境适应性；另一方面，需要进行舱段-支架-设备系统的动力学一体化设计，通过科学的管控手段，实现力学环境传递可控，从而确保飞行器的飞行可靠性和环境适应性。

由于飞行器局部曲率的原因，仪器、电缆等设备通常通过金属支架固定在舱壁上，仪器支架是设备直接感受到机械振动、冲击的最后关键环节。在工程上最常见的3种支架几何模型分别为簸箕形、几字形、盒形，如图1所示。

图1 典型的支架形式 Fig.1 Typical support forms: a) “dustpan” shaped supporter; b) “W” shaped supporter; c) “box” shaped supporter

在航天工程中，为了提高工艺可靠性，降低加工成本，金属支架往往为金属薄板通过钣金工艺得到。然而，在工程实际中发现，在舱段-支架-设备系统（见图2）中，从支架安装处到设备安装处的动力学传递特性有明显的放大特征，设备安装处的振动响应总均方根值是支架安装处的振动响应总均方根值的几倍甚至10倍以上，因此该系统的动力学响应主要由金属支架的动力学特性决定。从支架安装处到设备安装处动力学传递特性的显著放大会导致设备无法正常工作，甚至会导致飞行失利，严重影响飞行可靠性。然而，在实际工程研制中，对金属支架的设计一般只考虑结构、承载、接口等设计，不进行动力学设计，往往采取先设计、再生产、最后对整个系统进行试验验证的开环设计方法，然后通过一系列的“试错”试验后，把支架的结构方案确定下来，耗费大量人力物力。因此，如何将支架动力学设计融入支架结构设计，实现系统动力学传递特性的优化成为了近年来航天工程关注的一个重要问题。

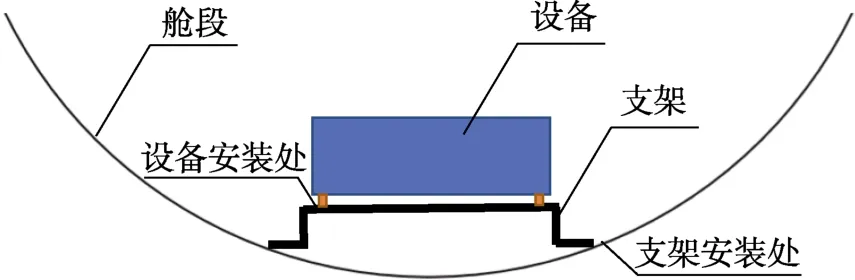
图2 舱段-支架-设备 Fig.2 Schematic diagram of cabin-supporter-equipment

在飞行器的方案设计和工程研制阶段，可以采用有限元法对飞行器结构进行动力学建模及数值仿真，从而得到随机振动条件下的结构振动响应分布，为结构优化设计打好基础。周芒等、唐远强等对典型结构的随机振动进行了试验和有限元仿真，得到了结构的振动响应。卢其进等、陈前等对海洋风电支撑结构在海洋环境下的动力学特性进行了分析和优化。葛文韬等研究了车载设备安装支架的疲劳仿真分析方法。李敏浩等、卢剑等开展了基于疲劳分析的车载设备安装支架结构方案优化研究，提高了支架的疲劳寿命。于忠杰等研究了船上设备支架的动力学特性，为结构方案的优化设计提供了重要基础。唐波、周江贝等研究了机载设备支架的振动特性和减振方案。张永存等研究了典型火炮结构在工作过程的瞬态响应，得到了前支架相关设计参数对振动响应的影响规律。徐立黄等、罗研朝等、张鹏飞等对飞行器设备支架结构的动特性进行了分析，获得了支架的模态、频响函数等特性参数。朱晓芳等、申智春等、王东升等对航天设备支架的振动响应进行了分析，并开展了方案的优化改进设计。柴国栋对某电台安装支架进行了随机振动分析。施云高等基于有限元对支架进行了轻量化力学分析。朱晓芳等研究了船舶尾轴架的固有频率计算方法，采用有限元法得到了支架的动力学特性参数。于韶明等研究了管路支架的振动试验方法，考核了支架及管路的环境适应性。张晓飞等、王云鹏等、文新海等研究了各种支架结构在外界振动环境作用下的应力和疲劳寿命分析方法。目前的工作主要集中在针对支架结构的动力学仿真分析及试验验证，对于工程上亟待解决的如何将支架动力学特性设计融入结构设计流程，以及如何通过支架的仿真分析、试验研究进行动力学特性设计的系统性研究较少。

基于此，文中提出了基于仪器支架随机振动响应预示的动力学特性管控方法，结合工程实际，设定动力学特性的优化目标，将支架动力学设计融入结构设计的流程中，形成了仪器支架的动力学特性管控方法，并在工程中得到应用。本文为支架结构振动分析和设计改进提供了可行的方法，避免了支架上设备安装处相对支架安装处的振动环境严重放大，为关键设备提供良好的力学环境，对飞行器环境工程和弹/箭环境适应性及可靠性提升具有重要意义。

1 仪器支架结构动力学

1.1 随机振动理论

复杂结构系统受到随机激励时，可以视为多自由度系统的受迫振动，其运动方程如下：

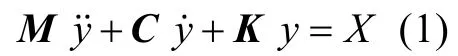
式中：为质量矩阵；为阻尼矩阵；为刚度矩阵；为系统响应；为激励。

对于该系统，如果系统本身的结构动力学参数（、、）都是确定的，而系统振源是随机的，则其输出响应也是随机的，所产生的振动就是随机振动。对于平稳随机过程，振源功率谱密度函数为S()，为频率，则结构振动响应的功率谱密度函数可以表示为：

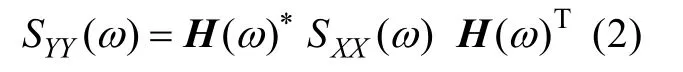
式中：()为系统的频率响应函数矩阵；上标“*”和“T”分别表示复共轭和转置。

对于时域上的平稳随机振动，其自相关函数为：

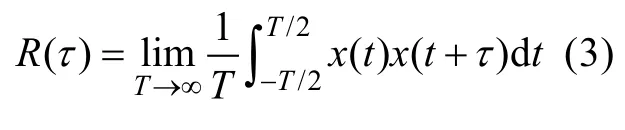
则功率谱密度为自相关函数的傅里叶变换为：

功率谱密度函数在频率的积分的均方根值为：

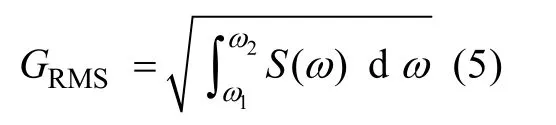
由上述随机振动理论可知，在准确地确定结构模型参数后，就可以方便地获得结构各个部位的随机振动响应。

1.2 动力学特性指标

为了将支架动力学特性融入支架结构设计中，需要构造合理的目标函数来表征支架的动力学特性。为了对工程中关注的仪器支架的动力学特性进行量化，提出了仪器支架的动力学特性指标，将其作为目标函数和结构优化变量的桥梁，实现通过结构优化对动力学特性进行管控。仪器支架的动力学特性指标的表征对象为舱段-支架-设备系统，舱段为边界条件，设备为负载。兼顾工程需求和问题的简化，提出了以下3个动力学特性指标。

1）基频值。基频值指的是支架第一阶弹性振动频率，是支架整体刚度的表征，选取该值便于在工程上对支架及其安装的刚度进行控制。基频大小与支架刚度、支架边界条件、支架上设备等因素有关。控制该参数，还可以避免支架与飞行器、设备及减振器的固有频率发生耦合。

2）放大倍数。放大倍数定义为支架上关键设备安装处的振动响应均方根值与支架安装处的基础激励振动环境均方根值的比值。放大倍数的大小与输入环境、支架动力学特性等因素均有关系，控制该参数，可以控制响应与输入间的传递关系。

3）一定频段内加速度幅频特性的最大值。幅频特性值是从支架安装处到设备安装处的传递函数在一定频段内谐振峰处的最大值。该值与结构设计、阻尼等因素有关。控制该参数，可以避免在特定频点发生异常的放大。

可根据不同情况选择其中的1个或几个来构造目标函数进行动力学特性的管控，也可以直接定义不同频段下从支架安装处到设备安装处的传递特性曲线作为控制要求。

2 随机振动响应分析

2.1 问题描述

以某热流变换器的盒形支架（见图3）为例开展振动响应的试验、建模和仿真分析研究工作。该支架上安装有3个热流变换器，分别为热流变换器1、热流变换器2、热流变换器3。热流变换器1—3通过螺接安装于顶部金属板上，其中热流变换器1、2质量为200 g，热流变换器3质量为150 g。

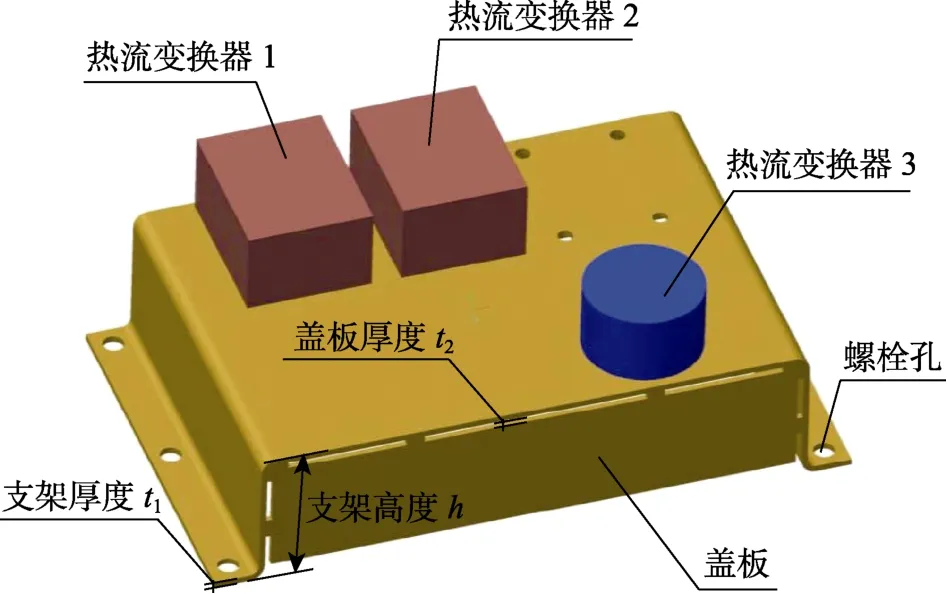
图3 热流变换器支架模型 Fig.3 Model of heat flux converter supporter

支架由厚度为的铝板经过钣金工艺，然后焊接厚度为的前后盖板得到。支架整体高度为，通过2个侧方向翻边的6个螺钉孔与飞行器舱壁螺接。支架材料的弹性模量为71 GPa，泊松比为0.33，密度为2 700 kg/m。

2.2 随机振动试验

为了得到支架的振动响应和放大情况，开展了振动试验，振动方向为垂直支架安装面。测点布置见图4。试验中振动加速度控制点设为支架安装处，振动加速度响应测点设置在热流变换器2安装处点。

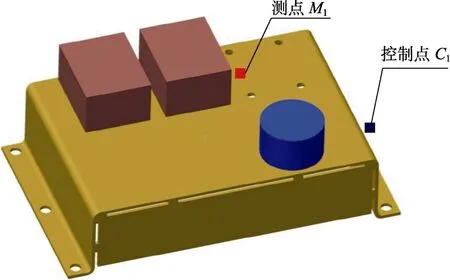
图4 试验测点布置 Fig.4 Test point layout

试验采用电磁式振动台进行，获得了支架安装处（）及设备安装处（）的振动响应，功率谱密度曲线见图5。可见该支架放大较严重，支架安装处的振动响应总均方根值为12.27，设备安装处测点的振动响应总均方根值为51.06。图5中100 Hz以内的低频部分，设备安装处和支架安装处有约2 dB的差异，分析认为主要原因是，振动台的振动传递到工装上在低频的存在一定的空间不均匀性，而支架由于承受多点不均匀的随机振动激励，导致低频并不是一比一的传递。

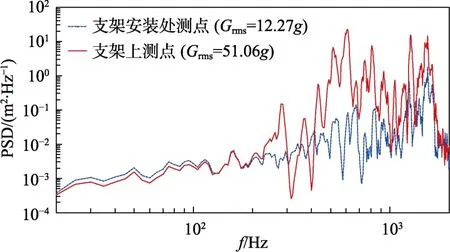
图5 振动响应实测数据 Fig.5 Vibration response of measured data

根据设备安装处测点与支架安装处测点振动响应的传递曲线（见图6）可知，支架在200 Hz以后有丰富的模态，并且在高频有严重的放大，是典型的壳体的振动响应。从传递函数曲线可以得到支架系统的各阶频率，前3阶频率分别为285、370、425 Hz。

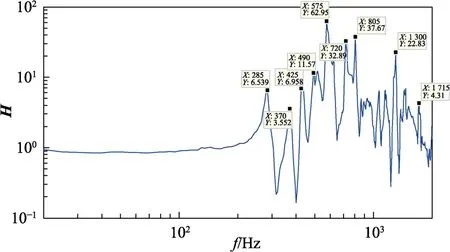
图6 传递函数 Fig.6 Transfer function

2.3 仿真分析

支架建模过程中考虑了支架厚度、螺钉、螺钉安装孔、金属翻边、局部倒圆角等特征，真实反映了支架的结构特性（如图7所示），为力学环境分析得到较为精确的分析结果提供了重要基础。在进行结构连接的建模中，主要进行了如下的考虑：设备上的螺钉与支架的螺钉孔采用固定连接；支架上的螺钉孔与舱段边界刚性连接；支架的翻边与舱段边界处理为接触连接。根据以往多次支架结构振动试验实测和模型修正的结果，系统的阻尼系数取为1.0%。

图7 有限元模型 Fig.7 Finite element model

采用ANSYS谱分析模块，给支架施加与试验中支架安装处振动响应一致的基础激励，可以得到结构各部位的振动响应。数值模拟得到的振动加速度响应云图见图8，试验测点位置处的振动响应功率谱密度曲线见图9。可见设备安装处振动量级的计算值为53.68，与实测值51.06基本一致，并且功率谱密度曲线与试验实测曲线趋势一致，低频的谐振峰吻合较好。功率谱曲线低频的差异主要是由于数值仿真时对基础激励进行了平滑处理造成的。

图8 结构加速度响应云图 Fig.8 Contour of structure acceleration response

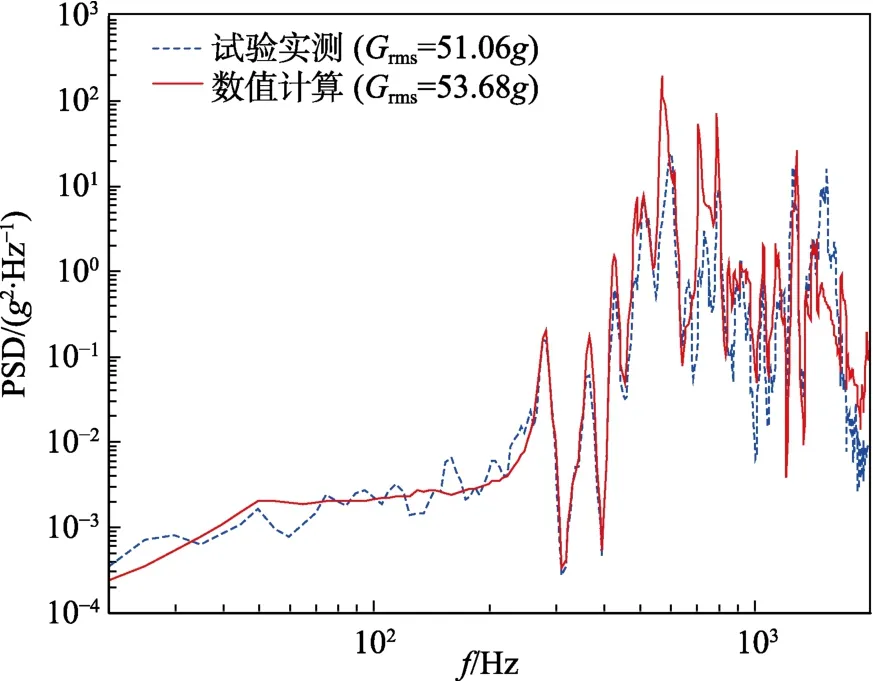
图9 支架上测点处响应功率谱密度 Fig.9 Response power spectral density at the measuring point on the equipment supporter

由于支架结构尺寸、测点尺寸及质量的限制，随机振动试验只能得到少数位置的振动响应。通过数值仿真可以得到整个结构各处的随机振动响应，这是对随机振动试验的重要补充。该建模与仿真方法可以较为准确地预示支架的随机振动响应。

对该问题选择基频和放大倍数这2个动力学特性指标进行分析。从传递函数曲线（见图6）可以得到支架系统的各阶频率，其一阶频率为285 Hz。分析支架安装处及设备安装处的振动响应，由图9可见，该支架放大较严重，支架安装处振动响应总均方根值为12.27，设备安装处的振动响应总均方根值为51.06，可见设备安装处相对支架安装处放大了4.2倍。

3 动力学管控方法

第2节采用的数值仿真方法可以较为准确地预示仪器支架的随机振动响应。在此基础上，提出了航天设备仪器支架动力学管控方法，将支架的动特性设计融入支架结构设计流程中，运用动力学仿真优化及振动试验验证的方法，实现了基于“仿真分析-设计优化迭代”与“振动试验确认”双链路的航天设备仪器支架动力学管控。

支架振动特性闭环管控实施方案如图10所示。具体流程为：明确支架动特性指标要求；对支架振动特性进行仿真分析；设置目标函数，开展迭代优化设计；对支架开展动力学试验，验证其动特性指标。

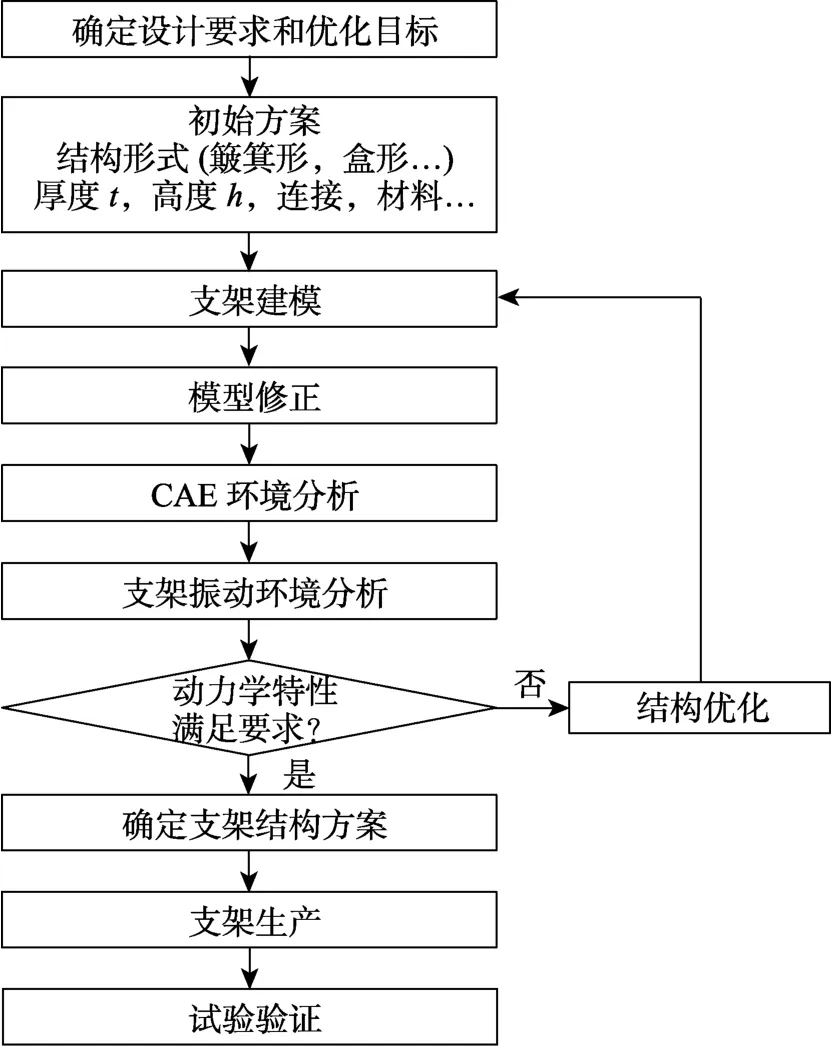
图10 支架振动特性闭环管控实施方案 Fig.10 The implementation of closed-loop control of the vibration characteristics of the equipment supporter

以第2节研究的支架为例，对其进行动力学管控。根据工程需要，该支架的动力学特性设计要求为：一阶频率高于180 Hz，振动量级放大倍数小于2。

由于选用了2个动特性指标，在优化分析中需要综合考虑这2个指标。采用统一目标函数进行优化分析，具有线性加权平方和的形式，见式（6）。

式中，加权因子w(=1,2,…,)的选取使得各分目标函数wf()成为具有等量级数值的无量纲函数。各分目标函数为：

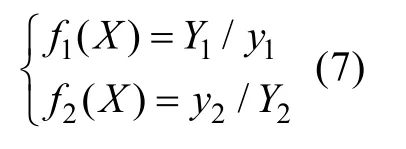
式中：、为给定的动力学特性指标值；、为仿真计算得到的动力学特性指标值。在本算例中，=180，=2，=0.3，=0.7。

对该支架进行随机振动仿真分析，得到的动特性指标为：一阶频率为285 Hz，振动量级放大倍数为4.2。

优化设计的方法有很多，如结构拓扑优化、参数 灵敏度分析等。由于支架设计不仅受动特性约束，主要还受空间、负载、接口的约束，以满足结构设计需求为主，设计变量的变化范围相对较小，因此采用灵敏度分析的方法，对支架结构进行优化设计。

在工程设计中，各参数一般进行圆整化处理，对支架厚度、盖板厚度、螺栓数量、支架高度4个参数在合理范围内进行灵敏度分析，结果如图11所示。根据灵敏度分析结果，选择支架厚度为4 mm、盖板厚度为2 mm、螺栓数量为8个、支架高度为45 mm，进行仿真。仿真得到的动特性指标为：一阶频率为183 Hz，振动量级放大倍数为1.67，满足指标要求。

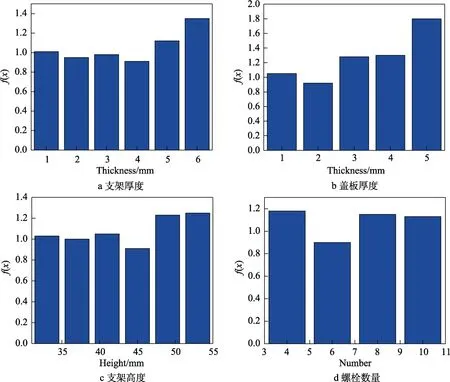
图11 各参数灵敏度分析结果 Fig.11 Sensitivity analysis results of each parameter: a) thickness of supporter; b) thickness of cover plate;c) height of supporter d) number of bolts

4 结论

本文基于典型仪器支架精确预示方法，提出了仪器支架的动力学特性管控流程，以动特性指标要求为目标，以随机振动响应的精确预示为途径，对仪器支架的动特性进行优化和管控，为支架结构振动分析和改进设计提供了可行的方法，可以降低对电子设备的环境适应性要求，降低研制成本。通过本文的工作可以得到如下结论。

1）通过对支架结构、连接、阻尼等进行合理建模，可以得到振动响应量级、低频功率谱密度曲线与试验吻合较好的数值仿真结果，实现了对仪器支架随机振动响应的精确预示。

2）提出了面向支架动特性管控的动力学特性指标：基频值、放大倍数、一定频段内加速度幅频特性的最大值。这3个动力学特性指标可以全面表征仪器支架在随机振动激励下的动力学特性，并可据此构造优化目标以对支架的动力学特性进行有效管控。

3）提出的典型仪器支架的动力学管控方法，实现了将支架动特性设计融入支架结构设计流程中，可在研制初期实现对支架动力学特性的有效管控。

本文给出了典型仪器支架的振动响应分析和动力学管控方法，将支架动特性设计融入支架结构设计的流程中，并经过航天工程实践验证有效，对于支架结构振动分析和设计改进提供了依据，对提高弹、箭环境适应性和可靠性具有重要意义。