基于模拟退火算法的加速器能谱重建
郭金森GUO Jin-sen;李传龙LI Chuan-long;王薇WANG Wei
(中国原子能科学研究院,北京102413)
0 引言
在利用加速器打靶的韧致辐射光子束进行治疗时,剂量计算软件为加速器TPS 治疗计划系统的基础。任何剂量计算程序都需要用到光子能谱数据。然而在实际的治疗系统中,有些情况下很难直接测量能谱数据。因此针对医用加速器,不同的研究者一直在探求获取准确能谱的方法[1]。主流方法有:一是利用蒙特拉罗方法模拟加速器治疗机头得到能谱,如Deng J 等人[2]在2000 年利用EGS4 程序模拟了来自瓦里安Clinac2100c 和2300c/d 加速器的4、6和15MV 光子束能谱。2015 年Fátima Padilla-Cabal 等人[3]利用MCNPX 和EGS 程序建立了医科达加速器的精确模型并做了剂量计算。这种方法能够保证所建能谱的精度,但前提是需要精确地知道准直器、均整器、电离室等部件的尺寸、材料等数据。二是利用射束穿过不同介质的透射数据得到X 射线能谱,典型如[4,5]等人的工作,该方法并不适用于高能光子射束。三是在射束中轴测量PDD 数据得到精确测量的前提下[6],利用数学方法进行能谱重建。如2001 年,Deng J[7]等人在研究了从电子束中心轴百分比深度剂量(PDD)曲线,采取“随机蠕变”(random creep)算法推导了临床电子和光子能谱,但该方法有可能收敛至局部最优解。2010 年北京大学姚杏红[8]等人采用Cimmino 方法重建瓦里安600CD 直线加速器X 射线能谱,该方法基于双源模型,结果比较精确,但大射野情况下重建能谱出现了病态解。2013 年陈元华[9]等人针对瓦里安15MV 光子束利用遗传算法优化重建了光子能谱,得到的能谱与蒙特卡洛模拟得到的能谱具有较好的一致性。2013 年刘娟[10]等人根据利用模拟退火算法重建了西门子医用加速器6MV X射线能谱。
模拟退火算法为化工、冶金工业术语,现在已经作为最优化算法用于各个行业。模拟退火算法的核心是在爬山算法的基础上增加Metropolis 准则,即从当前状态i→新状态j 时,即使新状态j 在某个规则下优于状态i,也以一定的概率接受状态j,否则仍保留状态i。模拟退火算法有一定的概率跳出局部最优解从而找到全局最优解。本文拟利用模拟退火算法,结合实验PDD 数据,对国内某型医用加速器6MV、18MV 能量下X 射线能谱进行重建,重建结果和蒙特卡罗模拟得到的能谱进行对比以验证可靠性。并为后续剂量计算程序开发奠定基础。
1 材料与方法
1.1 问题的数学描述
由测量PDD 和单能光子PDD 求解光子能谱的问题,可以描述为解线性方程组问题。假设加速器出射能谱可以离散化为E1,E2…En,其中E1~En为每个离散化能量区间的平均能量。n 组能量的按照注量加权的权重为ω1,ω2,…ωn,则应有如下如下线性方程组成立:

其中dij代表深度为i 处,Ei能量下的单能PDD 的剂量数据。Dj为深度为Hj处不同权重下的单能PDD 加权相加后的合成PDD 数据,在ω1,ω2,…ωn为实际能谱情况下,D1…Dm即为测量PDD 数据。该方程组一般为超定方程组,其解不止一个。因此需要找到最符合物理意义的一组解,即为能谱数据。可见,最优化的能谱可以使合成PDD 数据最接近测量PDD,也即相似度最高。为描述合成PDD(用量F 表示)和测量PDD(用M 表示)x 相似度,引入相关系数:

进行能谱重建。其中f(x)为目标函数,Fi为深度为Hi处的合成PDD,Mi为深度为Hi处的测量PDD。
1.2 单能光子PDD 以及能谱模拟
为获取(1)中的单能PDD,采用蒙特卡罗模拟程序BEAMnrc 的剂量计算程序xyznrc 进行模拟。模体为30cm×30cm×30cm 厚的水模,密度为1.0g/cm3。源皮距为100cm,射野为5cm×5cm。沿射野中心轴取1.5cm×1.5cm×0.1cm 体素共299 个。针对6MV 计算了17 个能量点的单能PDD 数据,针对18MV 则计算了23 个能量点,即公式(1)中n=23。所有模拟结果误差最大均不超过0.4%。
为验证重建能谱的准确性,利用蒙特卡罗模拟程序EGSnrc 建立了加速器治疗头模型,获取了治疗头6MV 和18MV 的出射能谱。加速器治疗头结构包括靶、初级准直器、均整器、电离室,次级准直器(上、下两个)等结构。通过控制上下次级准直器控制射野大小为5cm×5cm,分别模拟了6MeV 与18MeV 窄电子束入射情况下的韧致辐射谱。见图2,图3。
1.3 利用模拟退火算法重建光子能谱
在热力学上,一块被加热至高温的物体的降温过程被称之为“退火”。退火过程满足Metropolis 准则,即温度为T时,出现能量差为dE 的降温概率P(E)为:

即温度越高,出现一次能量差为dE 的降温的概率就越大;温度越低,相应概率就越小。
模拟退火算法的基本流程图见图1。

图1 模拟退火算法流程图
模拟退火算法基本流程为:
①对光子各能量箱赋予一定的权重,经验表明该权重不可过分偏离实际权重,否则可能导致收敛过慢甚至收敛至病态解。
②开始迭代过程,每一次迭代在每个能量箱上加一个小的随机量,即
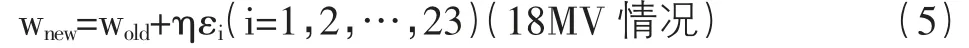
其中,η 为摄动系数,取0.00001,εi取[-1,1]之间的随机数。
③如果新的目标函数f(x)(见公式(3))小与当前目标函数,则接受新解和新的目标函数。如果新目标函数大于当前目标函数,则以概率P(C)=e-dC/T接受新解和新的目标函数。容易看出随着T 逐渐降低,越难接受“坏”的新解。迭代终止条件为目标函数低于某一个截止值,或模拟退火温度低于某个截止值。
模拟退火降温过程由初始温度T 及温度控制参数a表示,如下

这里初始温度取1×10-9,a 取0.999,每个温度出迭代100 次,取目标函数截止值Scut为4.6×10-5,即合成PDD 和测量PDD 之间的相关系数C=1-Scut即0.99954。
2 结果
图2、图3 分别为优化前后6MV、18MV 能谱和MC 模拟能谱对比图。二者均作了归一化处理。可以看出优化能谱和MC 模拟能谱峰位相同,谱形基本一致。计算得到相关系数均为0.99 以上。另外可以看出,图2 优化后能谱尾端有微小抬升,怀疑此处算法陷入局部最优解。但低能光子由于权重小对总剂量贡献较低。而高能部分两条能谱基本一致。图3 优化后能谱和MC 模拟能谱除个别点外也基本一致。

图2 优化后6MV 能谱和MC 模拟能谱对比图

图3 优化后18MV 能谱和MC 模拟能谱对比图
图4-图5 为优化前后6MV、18MV PDD 数据相对于测量数据的偏差。可以看出优化后绝大部分点相对误差在0.5%以下。

图4 优化前后后6MV PDD 相对测量数据的偏差

图5 优化前后18MV PDD 相对测量数据的偏差
3 讨论
本研究利用模拟退火算法,基于蒙特卡罗模拟的单能光子PDD 数据和测量得到的PDD,对医用电子加速器6MV、18MV X 射线能谱进行重建。计算得到的能谱与蒙卡程序直接模拟治疗头得到的能谱形状基本一致。
模拟退火算法具有全局搜索性,相比简单的爬山算法,有更大的概率得到全局最优解。需要指出的是,选择合适的初值仍然是有必要的,首先可以减小搜索时间,其次进一步降低收敛至局部最优解的风险。今后的工作将分为两步进行:①调整算法,尝试在迭代计算初期以更大的步长进行搜索,在目标函数f(x)满足一定条件时进行小步长精细化搜索,提高算法鲁棒性;②利用建成能谱开发卷积剂量计算程序。

