考虑级配参数空间变异性的堆石坝随机有限元分析

陆雪妮，朱 晟

(河海大学水利水电学院，江苏 南京 210024)

0 引 言

堆石坝工程中堆石料的级配变动会在很大程度上影响材料的物理力学性质，进而影响坝体的变形应力。已有研究表明，堆石料的物理力学特性与其级配分布紧密相关，李罡等[1]通过数值试验和室内试验研究，发现颗粒级配对材料应力应变关系的影响显著；赵婷婷等[2]基于颗粒流试验，发现表征颗粒级配分布的分形维数与堆石料的力学特性存在明显相关关系，可将分形维数用于量化分析堆石料的力学特性；加力别克等[3]根据一系列室内三轴压缩试验结果，整理了分形维数与邓肯E-B模型参数之间存在的二次函数关系。由此可见，堆石料的级配参数作为表征材料分布的重要参数，在堆石坝有限元计算中应当加以考虑，不可忽视堆石料级配效应对坝体力学响应的影响。朱晟等[4]结合不同级配堆石料的三轴试验结果，分析了堆石料级配参数与各力学特性之间的关系，基于广义塑性模型理论，建立了本构模型参数与分形维数之间的函数关系式，并验证了合理性，从而为考虑级配效应的有限元计算提供了有效途径。

目前，传统的确定性有限元计算方法对于大坝各分区材料均采用单一级配的假定，没有考虑到堆石料级配参数的空间变异性。即使是同一分区的堆石料，由于受到自然条件、母岩性质、填筑过程等多种因素影响，其级配参数也会存在分布上的空间变异性，这种空间变异性是与位置和距离紧密相关的。因此，为了可以更好地反映工程实际，可在考虑级配效应的有限元计算基础上，引入随机场理论和相关离散方法，用随机场的统计特性对堆石料级配参数的空间变异性进行表征，建立堆石料级配参数的三维随机场模型，结合考虑级配效应的堆石坝有限元分析方法对坝体力学响应进行研究。

本文以某抽水蓄能电站面板堆石坝作为工程实例，对堆石坝进行有限元网格剖分，整理统计堆石料的级配参数和静力计算本构模型参数，采用Cholesky分解法建立堆石料级配参数的三维空间随机场模型，结合考虑级配效应的堆石坝有限元分析方法，通过多次随机模拟，对随机计算结果进行统计分析，讨论堆石料级配参数的空间变异性对堆石坝变形安全的影响。

1 对数正态随机场模拟方法

已有众多学者[5-11]对堆石料材料参数随机场模型的建立展开研究，考虑到对数正态随机场在对数值大于零的模型参数进行模拟时的良好效果，研究中将筑坝堆石料材料参数均拟定为服从对数正态分布的随机变量。本文采用对数正态随机场对堆石料级配的分形维数进行随机模拟。

在随机场模型中，一般采用理论自相关函数来描述堆石料同一分区中两个不同空间位置处参数之间的自相关性[12]，由于高斯型自相关函数具有较好的平稳性，本文选用高斯型自相关函数进行表征，即

(1)

(2)

式中，δx、δy、δz分别为3个坐标方向上的波动范围；θx、θy、θz分别为3个坐标方向上的相关距离；τx=|xi-xj|，τy=|yi-yj|和τz=|zi-zj|为任意2个空间位置点之间的平行于坐标方向的间距。

对数正态随机场模拟方法的具体步骤为：

(1)根据有限元计算网格将随机场离散划分成一系列单元，令随机场单元与有限元单元一致，计算各单元中心点坐标(xi，yi，zi)，i=1， 2，…，ne，ne为随机场研究域内的单元数量。

(2)采用拉丁超立方抽样(LHS)方法随机生成独立标准正态空间随机向量ξ(ξ为含ne个随机抽样点的列向量)，经过m次随机抽样(m为随机模拟次数)，可以得到m个列向量。

(3)将步骤(1)得到的各单元中心点坐标代入式(1)，计算得到空间任意两点之间的自相关系数，构成自相关系数矩阵

(3)

当堆石料级配参数原始随机场为对数正态随机场时，需要将原始自相关矩阵C等概率转换成相应的标准正态空间的等效自相关系数C0，计算公式为

(4)

(4)采用Cholesky分解方法对上一步得到的等效自相关矩阵C0进行分解，得到下三角矩阵L(ne×ne)，乘上步骤(2)得到的独立标准正态随机向量样本ξ，即能够求得标准参数高斯随机场

(5)

然后结合均值μ、标准差σ等概率分布统计特征值，进行等概率变换，将上述得到的标准参数高斯随机场转换成相应的对数正态随机场，具体变换公式为

图1 大坝典型剖面示意

(6)

(5)以上过程实现了一次对数正态随机场的建立，对于步骤(2)中的m次随机抽样结果，将步骤(3)～步骤(4)进行m次重复，即实现了对数正态随机场的m次模拟与建立。

2 工程实例

2.1 单元网格剖分与荷载分级

根据所研究堆石坝工程的坝址地形及坝体分区资料，图1为大坝分区示意，模拟大坝填筑施工过程，逐级施加荷载，共分32级模拟大坝填筑过程，建立大坝三维有限元计算网格模型，如图2所示，共剖分网格节点59 298个，总单元57 359个，坝体底部施加固定约束。

图2 堆石坝有限元网格模型

2.2 堆石料级配参数空间随机场模拟

采用分形分布模型[13]拟合主堆石区、下游堆石区等主要分区坝料的颗粒级配曲线。对于堆石料，颗粒质量的分形分布模型为

(9)

式中，P(di)为小于di的颗粒质量分数；di为颗粒直径；dmax为最大粒径；D为分形维数。

结合施工填筑检测级配资料，其中主堆石料的实测级配数据共计147组，下游堆石料级配数据共计99组，拟合各分区坝料的颗粒级配曲线，如图3所示，相关系数均大于0.95，认为堆石料级配基本满足分形分布。

图3 堆石料填筑级配曲线

绘制分形维数的频率分布直方图和对数正态概率分布图，如图4、5所示，正态概率图用于检查一组数据是否服从正态分布，对主堆石区和下游堆石区的分形维数D取对数后绘制正态概率分布图，发现散点近似呈一条直线，说明主堆石区和下游堆石区的分形维数D满足对数正态分布。对各区分形维数D进行统计分析，根据3σ准则对各区分形维数D中含粗大误差的数据予以剔除，得到的各区参数分布范围为主堆石区2.34～2.71，下游堆石区2.44～2.71，见表1。

图4 主堆石区分形维数D概率统计规律

图5 下游堆石区分形维数D概率统计规律

表1 各区级配分形维数分布统计分析

表2 堆石料分形维数随机场的数字特征

在确定随机场特征值的基础上，根据前文所述对数正态随机场模拟方法，分别对主堆石区和下游堆石区的分形维数D进行随机模拟，采用中点映射法将各分区随机场中的分形维数D赋值给对应的坝体有限元网格单元，即可得出坝体堆石料分形维数的三维随机场。本文对堆石料分形维数随机场进行了200次随机模拟，根据其中一次随机模拟得到的堆石料分形维数D的三维随机场，绘制堆石料三维整体和最大断面的分形维数D的空间分布云图，如图6所示，发现主堆石区和下游堆石区的分形维数值分布没有明显的分界，主要原因是两个分区分形维数的统计特征值之间差异不大，且变异系数均较小。在建立三维随机场模型后，即可利用随机场模型中的分形维数值进行坝体有限元计算。

图6 主堆石区和下游堆石区的分形维数D的空间分布云图

图7 竣工期典型断面应力变形分布云图(单位：位移cm；应力MPa)

2.3 静力计算本构模型参数

计算采用可以反映堆石料剪胀性的统一广义塑性模型[16]。考虑级配效应对大坝有限元计算的影响，需要研究筑坝料级配参数与其力学特性之间的关系。已有研究[4]以大量堆石坝工程的试验结果为依据，分析了表征抗剪强度、剪胀性、压缩性等特性的参数与级配参数之间的关系，其建立的广义塑性模型参数与分形维数之间的函数关系式可将级配参数直接应用于堆石坝有限元计算中。本文主要研究考虑堆石料级配参数空间变异性时坝体的结构响应，因此对于库盆回填区、过渡区、垫层区等体积较小、对大坝主体影响较小的分区筑坝料，堆石料的分形维数按照单一级配的假定作均一化处理，仅探究对坝体变形应力影响较大的主堆石区和下游堆石区的分形维数随机分布。

对于主堆石区、下游堆石区的堆石料，需要考虑级配参数的空间变异性，对主堆石区、下游堆石区的堆石料级配参数随机场进行离散，实现足够多次数的对数正态随机场的模拟与建立，然后根据单元中心点的坐标，将所建随机场模型中的分形维数值一一映射到相应位置的网格单元中，根据分形维数与广义塑性模型参数之间对应的函数关系式[4]，完成堆石料单元级配参数与本构模型参数之间的映射，从而直接将级配参数直接应用于坝体有限元计算中。

2.4 考虑级配参数空间变异性的堆石坝三维有限元应力变形分析

以与图6随机场对应的随机有限元计算结果作为典型案例，选取坝体最大断面作为典型断面，整理竣工期堆石坝应力变形随机响应结果，如图7所示。图7中，位移竖直向上为正，竖直向下为负；水平位移向下游为正，向上游为负；压应力为正，拉应力为负。

由图7a可知，坝体沉降分布规律符合一般规律，坝体沉降较显著的位置主要集中于主堆石区、下游堆石区以及二者交界处。随机性有限元方法算得的竣工期坝体最大竖直沉降量为98.5 cm，位于下游次堆石区183.7 m高程附近，约1/2坝高处。

由图7b可知，坝体的水平向位移基本上主要指向下游，这主要是受到了向下游倾斜的坝基地形和堆石体的泊松效应两方面的影响。随机性有限元方法计算得到竣工期的水平向位移最大值为16.3 cm，指向下游方向，位于下游次堆石区的170.0 m高程附近。

由图7c、7d可知，竣工期的堆石坝大、小主应力的等值线分布均呈现出和坝坡近似平行的趋势，并且应力值随高程自上而下逐渐增大，在坝基处达到最大值。随机性有限元方法算得坝体大主应力最大值为2.92 MPa，位于主堆石区底部地基处；小主应力最大值为1.40 MPa，也位于主堆石区底部位置。

图8 随机有限元计算结果的统计稳定性(竣工期)

3 随机有限元计算结果分析

3.1 计算结果的统计稳定性

对坝体主堆石区和下游堆石区堆石料的分形维数分别进行200次随机模拟后，完成相应的随机有限元计算，在对200次随机有限元计算结果进行统计分析前，需要先判断经过多次随机模拟后的输出结果是否达到统计稳定状态。通过绘制随机计算结果的滑动平均值以及滑动标准差随模拟次数的波动曲线，作为判断随机模拟是否稳定的依据，若曲线波动性减弱、波动趋于平稳，则判定随机模拟计算结果达到稳定状态，认为随机模拟次数已足够。

滑动平均值Runava(n)和滑动标准差Runsd(n)分别定义为

(10)

(11)

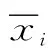
根据以上计算公式，将竣工期坝体竖直沉降、水平向位移、大主应力及小主应力等变形应力指标的最大值作为坝体响应值，绘制各响应值的滑动平均值Runava和滑动标准差Runsd随模拟次数变化的波动示意图，如图8所示。可以发现当随机模拟次数达到60次时，各响应值的波动曲线波动性均已减弱，曲线趋于平稳，当模拟次数达到140次以上曲线波动性已经非常稳定，认为曲线达到收敛状态。因此对坝体实现200次随机场模拟，认为随机模拟次数满足稳定要求，由此得到的统计分析结果足以很好地代表总体的统计特性。

3.2 统计分析

对200次随机有限元计算结果进行统计分析，统计特性如表3所示，由均值和标准差计算得到各响应值的变异系数分别为1.60%、1.56%、3.27%、1.85%、2.52%，各响应值的概率分布情况如图9、10所示。对坝体各随机响应值分别绘制正态概率分布图，用于检验是否服从正态分布，如图9、10所示，各响应值的正态概率分布图上的点可以较好地用直线拟合，认为满足正态分布，由此表明，堆石料级配的分形维数满足对数正态分布时，坝体应力变形基本满足正态分布。

3.3 与确定性有限元比较

如果不考虑堆石料级配参数的空间变异性，大坝各分区按照单一级配计算，即主堆石区、下游堆石区的分形维数取其平均值计算，作为确定性有限元计算结果，列于表4中。根据各坝体响应值的均值表征随机性有限元的计算结果，计算得到竣工期最大竖直沉降为97.8 cm，比确定性有限元方法算得的最大竖直沉降95.1 cm多出2.84%；最大水平向位移为16.3 cm，比确定性有限元方法算得的最大水平向位移16.0 cm多出1.88%；大主应力最大值为2.98 MPa，比确定性有限元方法算得的大主应力最大值2.85 MPa多出4.56%；小主应力最大值为1.43 MPa，比确定性有限元方法算得的小主应力最大值1.34 MPa多出6.72%。根据表4的计算结果比较情况可以看到，与忽略级配参数空间变异性的确定性有限元相比，随机性有限元的变形和应力均偏大，计算结果偏于安全，两者相对误差在2%～7%左右，由此可见，如果不考虑堆石料级配参数的空间变异性，很可能会在一定程度上低估坝体变形和应力。

表3 坝体200次随机模拟响应值的统计特性(竣工期)

图9 竣工期坝体变形概率统计规律

图10 竣工期坝体应力概率统计规律

表4 考虑级配参数空间变异性的随机有限元计算结果与确定性有限元对比(竣工期)

4 结 论

本文以某面板堆石坝工程为例，发展了基于Cholesky分解的堆石坝随机有限元计算方法，建立堆石料级配参数的三维随机场模型，结合考虑级配效应的堆石坝有限元分析方法对坝体力学响应进行研究，主要结论如下：

(1)堆石料级配曲线基本满足分形分布模型，分形维数D可较好地表征级配曲线，主堆石区、下游堆石区等分区的分形维数频率分布近似服从对数正态分布。

(2)基于Cholesky分解法实现堆石料分形维数的对数正态随机场模拟，并将随机参数映射至有限元分析模块，计算考虑级配参数空间变异性时的坝体结构响应分析。计算结果表明：当随机模拟至200次时，坝体各响应值达到统计稳定，且堆石料级配的分形维数满足对数正态分布时，算出的坝体应力变形基本满足正态分布。

(3)与坝料各分区参数采用单一级配假定的确定性有限元相比，随机性有限元的变形和应力均偏大，计算结果偏于安全，两者相对误差在2%～7%左右。如果不考虑堆石料级配参数的空间变异性，会在一定程度上低估坝体变形和应力。