一种基于SVD排列熵的电压暂降源分析方法

王子佳

（大唐环境产业集团股份有限公司，北京 100097）

0 引 言

电能质量是配电系统稳定运行的重点，减少电压暂降对系统的冲击是保证电能质量的重要指标之一。如何快速准确识别电压暂降源并采取相应措施，成为保证配电系统电能质量的难点[1]。近年来，众多学者通过大量研究后发现，引起电压暂降的工况不同，电压信号的突变程度各异。因此，准确提取电压突变信息是识别电压暂降源的关键。基于此，本文将奇异值分解（Singular Value Decomposition，SVD）排列熵方法引入电压暂降分析，通过对电压暂降信号进行SVD分解得到一系列包含突变信息的信号分量，然后对信号分量求取排列熵，提取突变特征，实现对电压暂降源的分析和识别。

1 SVD排列熵

1.1 SVD理论

SVD是一种通过将信号信息展开，呈现信息特征的分析方法[2]。对于m×n阶矩阵A，存在正交矩阵U和V，使得：

式中：

式（1）为矩阵A的奇异值分解，其中σi为A的奇异值，数值依次递减。

由于电压信号为一维向量，因此选取合适的矩阵形式是利用SVD理论的前提[3]。本文采用连续截断的矩阵构成方式，取正整数m和n，构成连续截断矩阵A为：

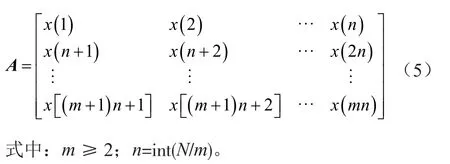
电压信号的突变信息主要体现在奇异值的数值上，随着奇异值逐渐变小，包含的突变信息也越来越少。假设第k个开始数值明显趋于零，则可确定电压信号的突变信息包含在前k-1个奇异值中。选取前k-1个奇异值重构矩阵，得到排除原电压信号中干扰信息的矩阵A'，便于准确提取电压突变信号特征。

1.2 排列熵

排列熵是一种对信号突变特别敏感的非线性分析方法[4]。通过对一维向量x(i)=[x1,x2,xN]进行重构，选取合适的嵌入维数m和延迟时间δ，则可得到：

将X(i)按照升序方式重新排列可得：

由式（7）可知，所有向量均可得到相应的符号序列[j1,j2,…,jN]，假设符号序列出现的概率为Pk，则其排列熵Hp为：

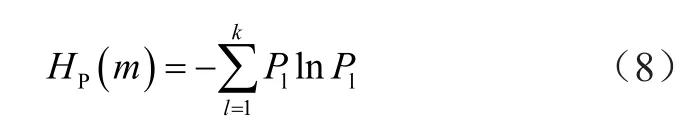
式中：l=1,2,…,k，且k≤m!。为统计方便，最后需对排列熵进行归一化处理。

2 基于SVD排列熵分析方法

由上分析，本文提出一种基于SVD排列熵的电压暂降源分析方法，首先对电压信号构造连续截断矩阵进行SVD分析，选取包含突变信息的奇异值重构信号，计算其排列熵，组成特征向量进行电压暂降源分析识别，具体步骤如下。

（1）对电压暂降信号采样，得到N个样本x1,x2,xt,…，xN；（2）对样本xt构造连续截断矩阵X，进行奇异值分解，得到一系列包含突变信息的奇异值矩阵，即S=diag(σ1,σ2,…,σi)；（3）确定奇异值明显趋于零的k值，选取前k-1个奇异值重构矩阵X'=[x'(1),x'(i),…x'(k-1)]；（4）选取合适的嵌入维数m和延迟时间δ，计算x'(i)的排列熵，构建特征向量T=[e1,e2,…,ek-1]，识别电压暂降源类型。该方法实现的流程如图1所示。

图1 基于SVD排列熵的电压暂降源分析方法流程

3 仿真验证

为了验证方法的可行性，将所提方法应用于配电网电压暂降仿真实验数据。参照文献[5]搭建火电厂配电仿真系统，如图2所示。

图2 火电厂配电仿真系统结构图

配电仿真系统由10 kV和0.4 kV两级构成。通过设置平台模块参数，分别模拟正常工况、线路短路、变压器投运以及电动机启动引起电压暂降的典型工况。仿真系统的采样频率为1 kHz，每种暂降源在0.4 kV侧各采集100组样本，每组样本包含1000个数据，随机选取50组作为实验数据。

3.1 样本信号

正常情况下，电压为0.38 kV的周期性正弦波，如图3所示。

图3 正常电压波形

以电动机启动工况为例，当0.4 kV低压侧有电动机启动时，系统母线电压幅值会出现短暂降低，并在电动机启动完毕时恢复到正常电压幅值，如图4所示。

图4 电动机启动时电压波形图

3.2 样本分析

分别对正常、线路短路、变压器投运以及电动机启动4种工况的样本向量构造10行100列的连续截断矩阵，进行奇异值分解。经奇异值分布对比后，选取前5个奇异值重构，重构后的矩阵为5行100列。分别求取重构矩阵行向量的排列熵，结果如表1所示。

表1 4种工况的排列熵分布

由表1可知，不同工况的排列熵强度和分布均不相同。将排列熵构建特征向量T=[e1,e2,…,e5]，可见不同工况的电压暂降特征存在较明显的阶梯分布，具有较好的识别性。

4 结 论

本文提出一种基于SVD排列熵的电压暂降源分析方法，有效解决配电系统造成电压暂降的工况识别。利用SVD排列熵构建特征向量，对电压信号暂降特征进行分析识别。仿真实验证明了本文方法的有效性，为配电系统电压暂降的分析提供了新途径。