基于NCD与优化函数结合的整流控制系统设计

吴连波，张小龙，刘华青，许孔孔

（1.西安航天动力测控技术研究所，陕西 西安 710025；2.空军装备部驻西安地区第八军事代表室，陕西 西安 710025）

0 引 言

晶闸管整流技术在通信系统、交通运输、电力系统以及工业等领域有着广泛应用[1,2]。传统的模拟触发电路控制线路复杂，不易调试，可靠性低，且触发信号精度不高，与预期波形相差较大。本文采用STM32F429微控制器作为数字化控制器，通过软件调节触发角，为晶闸管智能控制模块提供控制信号，具有较高的精度。为更快、更好地实现对调节器的设计，引入参考文献[3]中介绍的调节器工程设计方法。该方法通过合理的近似化简方法，降低系统阶次，以降低调节器的复杂程度。通过运算放大器或数字化控制器实现精确的控制规律，进而将系统校正为几种特定的低阶系统[4-9]。再结合总结的公式和图表计算调节器参数，可快速实现控制系统调节器结构参数的设计[10]。

1 系统建模

系统由整流、滤波、负载、采样以及控制等多个环节组成，建立控制系统的数学模型是分析和设计控制系统的首要工作。现主要对晶闸管整流装置和控制系统的建模过程进行分析。

1.1 晶闸管整流装置特性分析与建模

晶闸管整流装置传递函数当做一阶惯性环节处理后，能通过线性控制理论对其进行分析和设计。

1.2 控制器设计建模

为降低设计的难度，根据设计过程中的规律，利用MATLAB中的非线性最小平方函数，按照最小平方指标J=∫e2dt进行PID参数寻优，得到较优的PID参数kp(比例)、ki（积分）、kd（微分），并在此基础上再进行NCD优化，得到最终的kp、ki、kd。其中最小平方函数为：

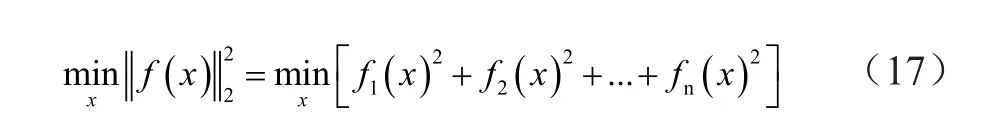
1.3 基于NCD优化仿真模型设计

结合上述方法对电压电流反馈控制方式的晶闸管整流系统的设计，采用Simulink工具箱建立控制系统仿真模型，如图1所示。

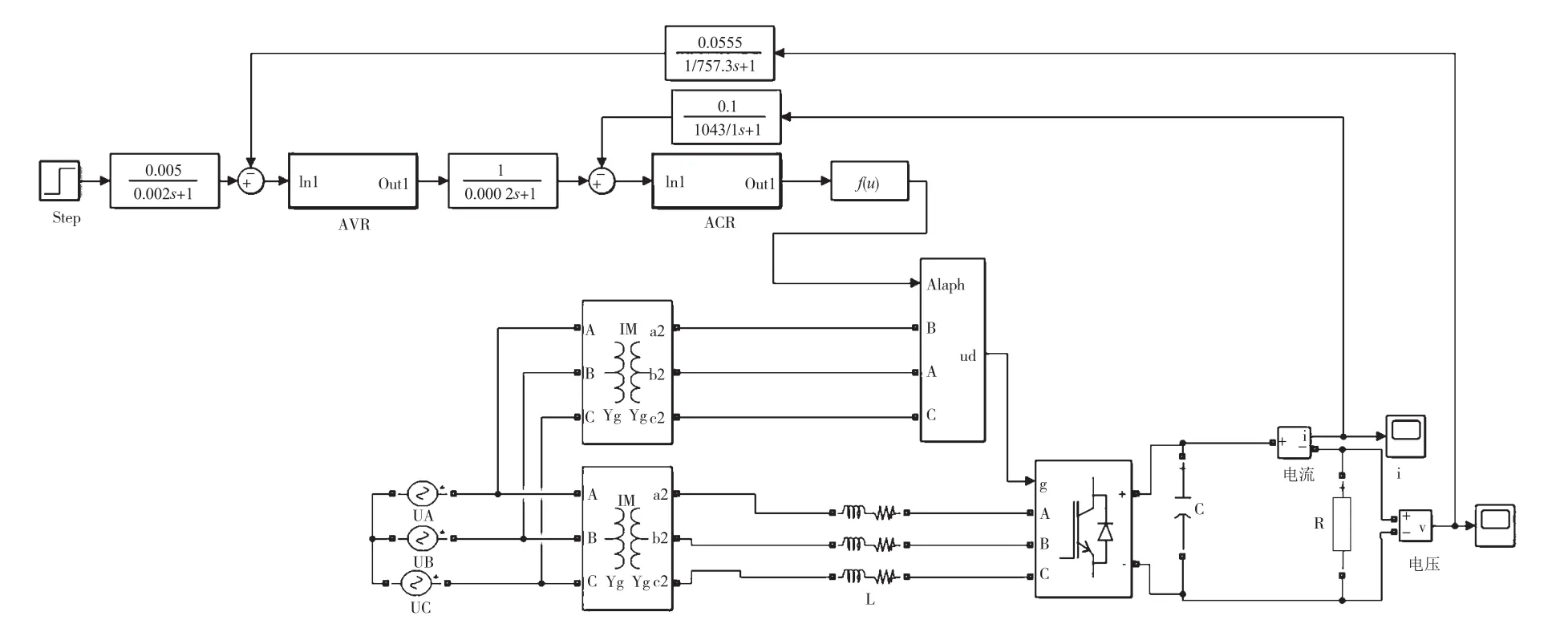
图1 电压电流反馈控制晶闸管整流系统仿真模型

对NCD Output模块按照表1进行参数设置，定义阶跃响应性能指标、调整变量及相关参数、变量允许误差。约束允许误差，通过菜单中“Edit”下“Axes Properties”命令定义优化时间和响应范围。设置优化时间（X轴）为0～100 s，阶跃响应范围（Y轴）为0～ 1.2。

表1 参数设定指标

2 电压电流反馈控制晶闸管整流系统仿真

ua、ub和uc构成系统三相交流电源，每相电压有效值为220 V。三相变压器采用Y-Δ联结组，变比为1.482，一次侧电压值为380 V，二次侧电压值为256 V。Universal Bridge为晶闸管构成的三相全控整流桥，保持默认设置不变。根据设计的电压调节器传递函数，搭建了如图2所示的电压调节器（Automatic Voltage Regulator，AVR）仿真模型。

图2 AVR子系统仿真结构

根据设计的电流调节器传递函数，搭建如图3所示的电流调节器（Automatic Current Regulator，ACR）仿真模型。

图3 ACR系统仿真结构

为验证仿真系统在电压发生波动时的控制效果，t=1.2 s时将ua、ub、uc三相交流电源的电压有效值增加为230 V，当t=1.8 s时将三相交流电源的电压有效值恢复到220 V，获得如下仿真结果。

负载两端电压Ud的波形如图4所示，电压波动及稳定时的波形如图5和图6所示，与电压反馈控制方式的晶闸管整流系统相比系统超调量很小，但调节时间更长。

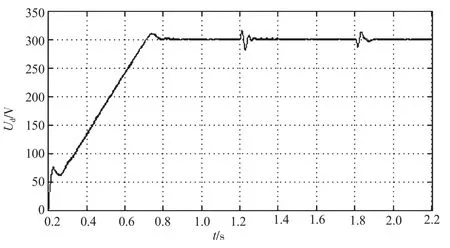
图4 负载两端的电压波形

图5 电压波动波形

图6 稳定时电压波形

晶闸管整流桥的输出电流Id如图7所示，稳定时的细节如图8所示。此时系统电流最大值为14 A，在系统允许范围内，电流反馈对晶闸管整流桥输出电流起到明显的调节作用。

图7 输出电流Id的波形

图8 稳定时Id波形细节

3 系统硬件平台验证

对系统反馈环节和触发环节进行校准后，测试实际系统的控制效果。测试时所选负载的阻值为45 Ω，受其额定电流限制，测试时设定输出直流电压为150 V。系统稳定时，触发角α=13°，获得如图9和图10所示的结果。

图9 电压波形

图10 稳定时电压波形

由图10可知，输出电压最大值与最小值之差ΔUd=6.92 V。

稳定时Id波形细节如图11所示，电压波动时Ud波形如图12所示，闭环控制系统对电源电压波动有较好的抑制效果，反馈控制可使被反馈量稳定在期望值附近。

图11 稳定时Id波形细节

图12 电压波动时Ud波形

4 结 论

本文在仿真环境下建立了NCD与优化函数结合的整流控制系统仿真模型，并进行了仿真。而后介绍了实际系统的调试过程，并对电压反馈方式的控制效果进行了测试。通过分析仿真和测试结果得出以下结论，即电压、电流双闭环控制系统对电流超调起到起到抑制作用，使晶闸管整流桥输出电流Id在系统允许范围内。