Nyquist第一准则的理解与应用

王 霞，王卓然

（云南民族大学 电气信息工程学院，云南 昆明 650504）

0 引 言

“通信原理”课程是通信工程、电子信息类专业本科生的一门重要的专业基础课，课程在学科体系中起承上启下的作用，一直备受教师和学生的高度重视[1]。然而，该课程涉及公式、定理较多，推导过程烦琐，相对枯燥的理论知识让大部分学生对课程的学习兴趣不大，课堂教学存在一定难度[2]。数字基带传输系统是“通信原理”课程的重点内容之一，也是数字通信的基础。如何消除码间串扰、如何降低噪声对信号的影响是所有数字通信系统都必须要解决的两个基本问题[3]。根据数字通信原理，基带传输系统若要实现无码间干扰传输，则基带系统总的传输特性必须满足Nyquist第一准则。部分学生对Nyquist第一准则的理解困难，运用Nyquist第一准则分析实际问题更是无从下手[4]。本文从实践出发，针对基带传输系统的码间干扰问题，从原理上阐述了基带系统无码间干扰的条件，即Nyquist第一准则。

1 数字基带传输系统模型与Nyquist第一准则

基带传输系统的传输特性的模型如图1所示。设发送滤波器、信道、接收滤波器总的传输特性为H(ω)，则有H(ω)=GT(ω)×C(ω)×GR(ω)。

图1 基带传输系统模型

要使基带传输系统实现无码间干扰传输，则系统的传输特性H(ω)应满足：

式中：C为常数；T为传输码元的时间间隔。

基带系统的总特性H(ω)凡能满足此要求的，均可以消除基带系统的码间干扰，该条件称为Nyquist第一准则。一般地，定义理想基带传输系统的传码率RB=1/T为奈奎斯特速率，其带宽B=(π/T)/2π=1/2T为奈奎斯特带宽，T为奈奎斯特间隔。如果系统以高于1/T的速率进行传输时，将存在码间干扰；如果系统以低于1/T的速率进行传输时，有可能存在码间干扰，也有可能无码间干扰。奈奎斯特速率是系统实现无码间干扰传输时能达到的最大速率，此时的系统最高频带利用率为2 Baud/Hz。推广到一般系统有，当系统的频率为ω时，该系统无码间干扰时最高的传输速率（即奈奎斯特速率）为2ω。

由传码率RB与T的关系，可得到该判据式（1）的等价描述为：

判断某传输系统是否满足无码间干扰传输，有两种方法。

方法一：把一个基带传输系统的传输特性H(ω)等间隔分割为2π/T宽度，若各段在(-π/T, π/T) 区间内能叠加成一条直线，那么它在以RB=1/T的速率传输基带信号时，就能做到无码间串扰传输。

方法二：由H(ω)确定系统的奈奎斯特等效带宽BN，然后。由RBmax=2BN求出最大码速率，再与实际码速率比较，若RBmax/RB为正整数，则无码间干扰，否则有码间干扰。

2 Nyquist第一准则的应用

下面通过一个实例来分析系统满足无码间串扰传输的条件，即Nyquist第一准则的具体应用。假设基带系统的频率特性如图2所示。若以2/T速率传输信号，判断各系统是否存在码间串扰。若以8/T速率传输信息，各系统以几进制码元传输时可以实现无码间串扰。

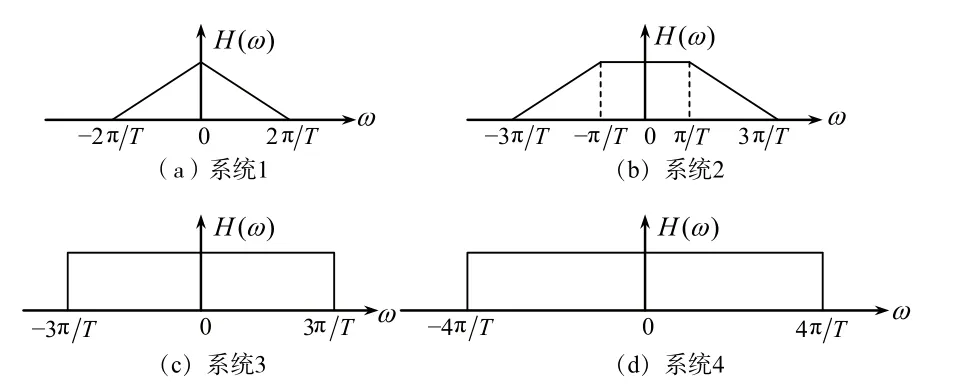
图2 4种不同基带系统的频率特性

（1）首先分析第一个问题，判断各系统是否存在码间串扰。

根据式（1）和题中给出的条件RB=2/T可知，要使系统实现无码间串扰，必须满足的条件为：

分别将图2（a）、（b）、（c）、（d）4个系统按照该平移量进行平移叠加，然后在观察区间内检验最后叠加的结果是不是一条水平直线。按照该方法可知：在RB=2/T的码速率下，（a）和（c）系统不能实现无码间串扰，（b）和（d）系统可以实现无码间串扰。

此外，分析介绍一种根据系统频率特性H(ω)分析码间干扰特性的简便方法。由H(ω)确定系统的奈奎斯特等效带宽BN，然后。由RBmax=2BN求出最大码速率，再与实际码速率比较，若RBmax/RB为正整数，则无码间干扰，否则有码间干扰。下面对这一方法进行简要分析。

首先介绍理想基带传输系统的奈奎斯特带宽。理想基带传输系统的传输特性具有理想低通特性，其传输函数为为：

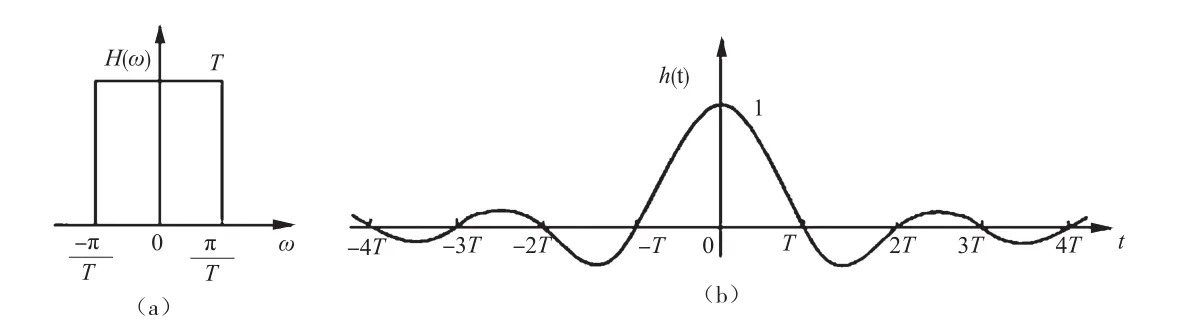
图3 理想低通系统的频域与时域波形

对于图3（a），当系统传码率为RB=1/T时，根据Nyquist第一准则的频域条件可以判断，系统无码间串扰。从时域的角度观察图3（b）可以看到，理想低通信号h(t)在t=±nT(n≠0)时有周期性零点。如果发送码元波形的时间间隔为T，接收端在t=±nT(n≠0)时抽样，就能达到无码间串扰，如图4所示。

图4 无码间串扰示意图

由图4可见，输入数据若以RB=1/T的波特速率传送时，在各个T的整数倍处的数值仅由本码元所决定。其他各码元对应的输出响应在此处均为零，即各码元之间没有相互干扰。因此，如果在T的整数倍处进行抽样判决，就可以正确地恢复出“1”码和“0”码。但若不满足RB=1/T的条件，在各个T的整数倍处，其他各码元的输出响应将不会为零，即各码元的输出响应是相互影响的，此时存在码间相互干扰。如果在此处抽样判决，由于码间干扰，容易出现误码。由此定义理想基带传输系统的传码率RB=1/T为奈奎斯特速率，其带宽B=(π/T)/2π=1/2T为奈奎斯特带宽，T为奈奎斯特间隔。如果系统用高于1/T的速率进行传输时，将存在码间干扰，如果系统用低于1/T的速率进行传输时，有可能存在码间干扰，也有可能无码间干扰。奈奎斯特速率是系统实现无码间干扰传输时能达到的最大速率，此时的系统最高频带利用率为2 B/Hz。推广到更一般的系统可以得到，当系统的频率为ω时，该系统无码间干扰时最高的传输速率（即奈圭斯特速率）为2ω。

使用该方法需要得到系统的奈奎斯特等效带宽，也就是将给定的系统等效为理想基带传输系统后的奈奎斯特带宽。根据该方法可得：

根据题中所给条件RB=2/T：

对于系统（a），RaBmax/RB=1/2≠整数，故系统（a）有码间串扰；

对于系统（b），RbBmax/RB=1=整数，故系统（b）无码间串扰；

对于系统（c），RcBmax/RB=3/2≠整数，故系统（c）有码间串扰；

对于系统（d），RdBmax/RB=2=整数，故系统（d）无码间串扰。

根据题中所给条件Rb=8/T，可以得到此时的码速率RB=Rb/log2M=(8/T)/N=8/TN，其中令N=log2M为正整数，M就是系统所采取的进制数。为了使系统满足无码间串扰，必须满足条件RBmax/RB为正整数。令RBmax/RB=n，n为正整数。

对于系统（a），RaBmax/RB=Na/8=n，从而Na=8n，M=28n，n为正整数；

对于系统（b），RbBmax/RB=Nb/4=n，从而Nb=4n，M=24n，n为正整数；

对于系统（c），RcBmax/RB=3Nb//=n，从而Nc=8n/3，M=28n/3，考虑到M和n都必须为正整数，所以此时n取3的倍数的正整数；

对于系统(d），RdBmax/RB=Nd/2=n，从而Nd=2n，M=22n，n为正整数。

3 结 论

在数字基带传输系统中，码间干扰是影响通信质量的主要决定性因素。本文在对数字基带传输系统进行分析的基础上，总结了判断数字基带传输系统是否存在码间干扰的两种分析方法，并通过一个具体例子探讨了奈奎斯特准则的理解和应用。