基于小波分析的月售电量预测方法
王梓屹,王越涵
(国网抚顺供电公司,辽宁 抚顺 113008)
1 概述
2020年,国家发展改革委、国家能源局联合修订印发《电力中长期交易基本规则》(发改能源规〔2020〕889号)。售电公司作为零售市场的主体,担任着从市场购买电能,并出售给用户的中间商角色。在电力交易过程中,售电公司面临着市场价格和用户侧负荷双重波动的风险。利用精确的月售电量预测结果制定合理的购售电策略来提高效益,是售电公司面临的关键问题。因此,提高月售电量预测精度的研究具有重要意义[1-3]。
综合国内外月售电量预测方法发现,售电公司普遍使用相对成熟可靠的时间序列法。但是模型本身存在缺点,时间序列适用于变化平稳、变化趋势明显的月售电量序列,如果直接对不平稳的月售电量时间序列进行预测,达不到预想的精度[4-13]。
本文在上述研究的基础上提出了基于小波分析的灰色和自回归移动平均(auto regressive integrated moving average,ARIMA)预测方法。
小波分析是一种变换方法,能够通过小波变换提取出被分析量时域和频域的信息用来分析,先将月售电量序列的逐月增长特性与随机波动特性分解成2种子序列,此时非平稳的待预测月售电量序列就被分为增长特性子序列和平稳波动子序列这2种子序列。经过上述分解之后再针对这2种子序列的特点分别选取最适合的预测模型进行预测。通过对这2种子序列的预测结果进行小波重构,最后得到最终的预测结果。本文预测策略结构如图1所示。

图1 本文预测策略结构
2 小波分析在月售电量预测中的应用
2.1 小波分析概述
小波分析可以从数学角度和应用角度2个角度来看。小波分析既是包括函数空间、广义函数、傅里叶分析、抽象调和分析这些的总结,又是工程应用上的突破。本文研究的月售电量序列可看成一种信号,这种信号既有时域部分又有频域部分,所以使用小波分析势在必行[9-13]。
2.2 小波分解与重构
基于Mallat得出的结论,其分解及重构思想:设Hjf为信号S在分辨率2j下的近似分量,那么Hjf就可以进一步分解为f在分辨率2j-1下的近似分量Hj-1f和位于分辨率2j-1与2j之间的细节分量Dj-1f,分解过程如图2所示。

图2 信号不同频带分解过程
由于每一次分解都经历一次降采样,而月售电量序列总长度不变,所以每次分解时候得到的近似序列和细节序列都要减小为原来的一半。
2.3 几种常见的小波
表1介绍了几种常见的小波。
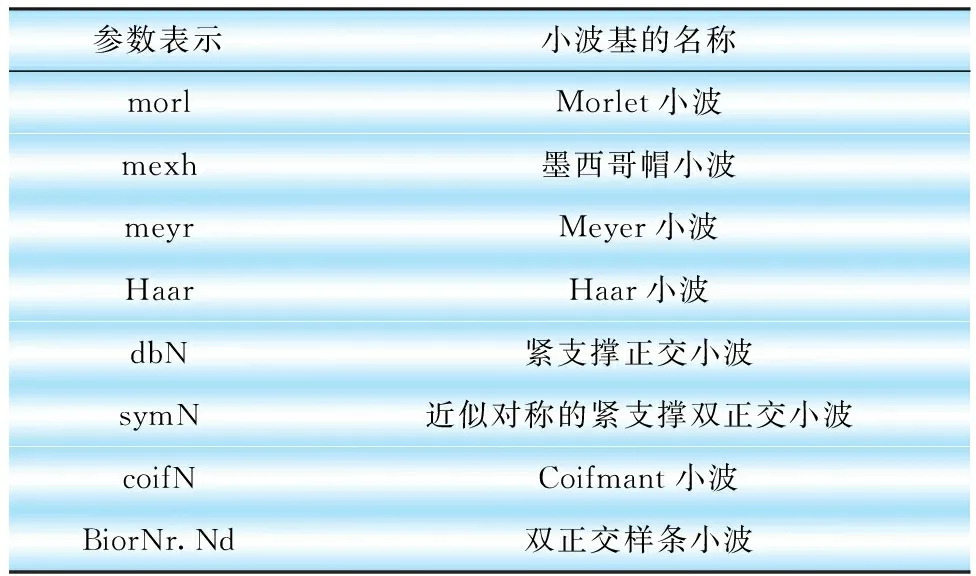
表1 MATLAB对应的小波函数
3 灰色与时间序列预测理论
3.1 灰色系统理论概述
1982年,中国学者邓聚龙创造出了一种新的预测方法——灰理论。由于灰理论特别适用于数据特别少而且还不足够明确的情况,所以适合月售电量的预测。灰色系统理论使用灰色模型(grey model,GM)进行预测,记GM(m,n),表示对n个变量建立m阶微分方程,可用于数列、灾变、拓扑、系统预测等方面[4]。
3.2 时间序列理论概述
时间序列就是指数据按照时间顺序排列的序列,是按照一定的时间间隔来排列的。月售电量就是一个典型的时间序列。1927年,G.U.Yule提出了自回归(auto regressive,AR)模型,几年后G.T.
Walker提出了移动平均(moving average,MA)模型和自回归移动平均(auto regressive moving average,ARMA)模型。1970年,Box和Jenkin共同提出了整合ARIMA模型。ARMA模型是在AR模型和MA模型的基础上增加了一个判断模型的算式,但是局限于处理平稳数据;ARMA模型加入差分算法后得到ARIMA模型,能够将非平稳序列变平稳,从而进行预测[4-16]。
4 案例仿真分析
对实际案例进行分析预测,基于某市10年共120个月度月售电量数据,如图3所示,以前108个月数据作为样本,预测出12个月的数据,并提取出后12个月数据进行对比,得出模型的误差进行分析探讨。
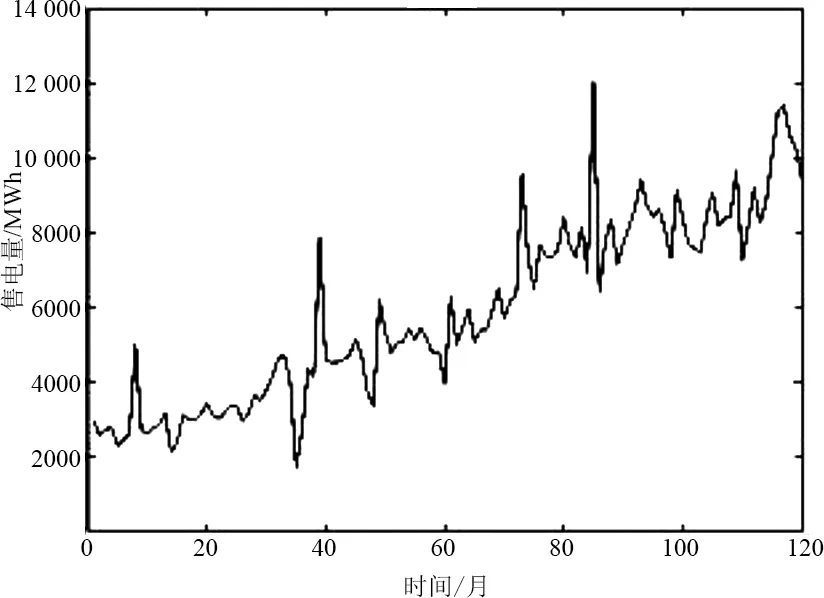
图3 原月售电量曲线
预测误差的大小是判断预测方法优劣的根本依据,这里介绍4种常用的方法。
a.相对误差
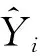
b.平均相对误差
c.均方误差
d.均方根误差
本文将通过计算预测结果的相对误差、平均相对误差和均方根误差来判断预测模型的精度[8,11-13]。
4.1 小波分解
首先要确定小波基函数和需要分解的尺度,表2为各小波基特性比较,文献[10-11]指出对于电力系统月售电量序列的增长和波动特性,采用近似对称、光滑的紧支撑双正交小波Daubechies作为小波基是合适的。

表2 小波基特性比较
表3为不同小波基分解的最大尺度,根据文献[12]使用MATLAB自带的Wmaxlev函数来确定最大分解尺度。

表3 分解的最大尺度
经过大量运算之后本文选取了db3作为小波基,并对月售电量序列进行3尺度分解。
图4为分解流程,对某市120个月售电量数据进行上述小波分解,结果如图5所示,得到6个细节分量和近似分量。由于ca2和cd2来自于ca1,而ca3和cd3来自于ca2,所以只需要预测出cd1、cd2、cd3和ca3即可。
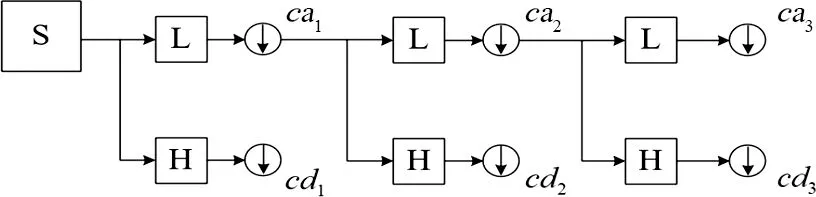
图4 小波分解流程
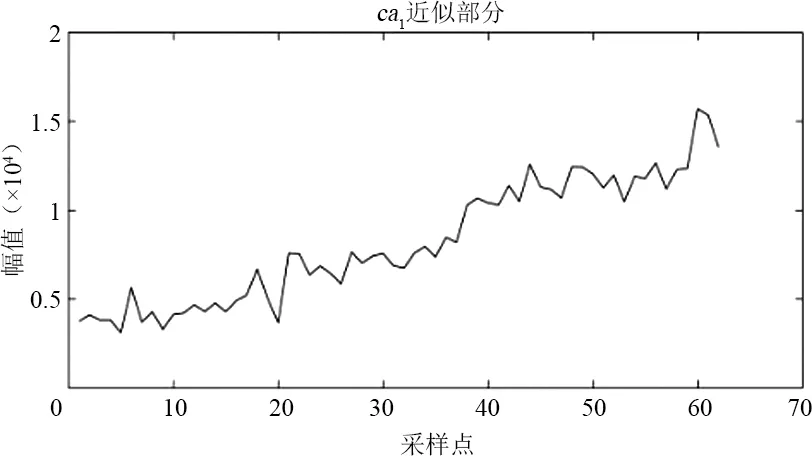
(a)
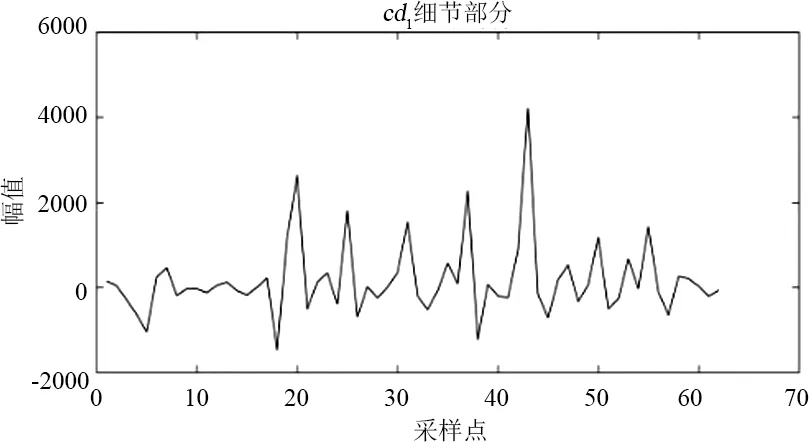
(b)
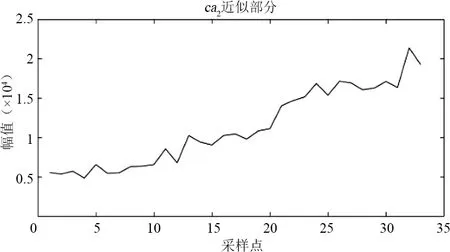
(c)
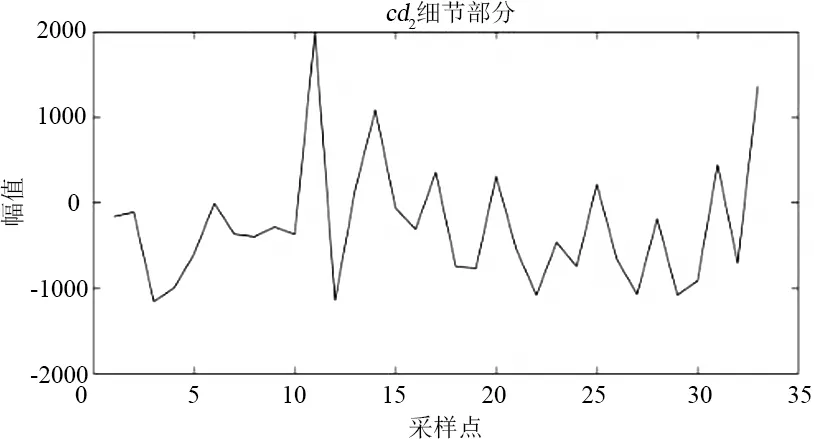
(d)
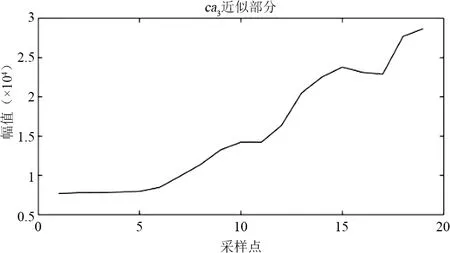
(e)
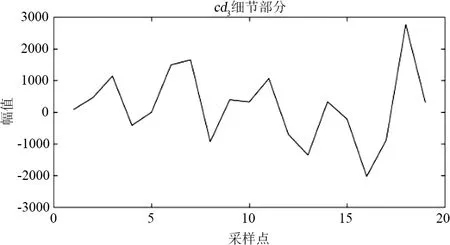
(f)图5 小波分解结果
小波逆变换也叫做小波重构,正好与分解相反,首先进行升采样,即为隔点插零。小波分解和重构的全过程如图6所示。重构后4个分量直接相加可得总预测结果见式(1)。
S=d1+d2+d3+a3
(1)
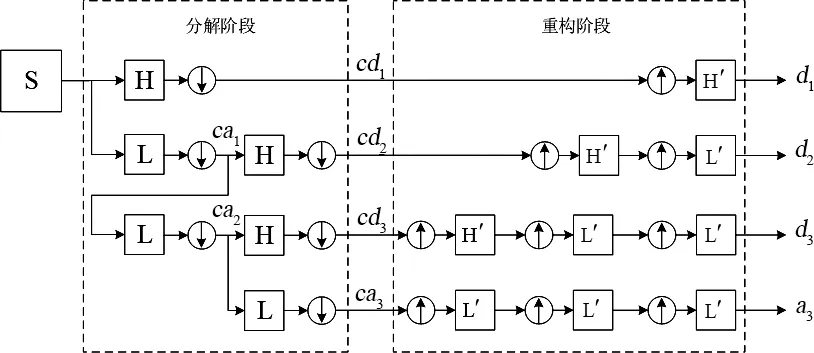
图6 小波分解重构全过程
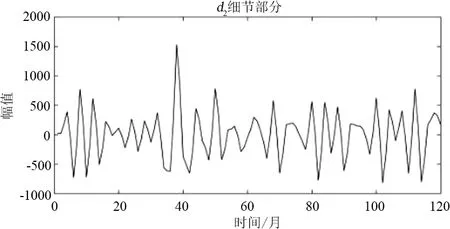
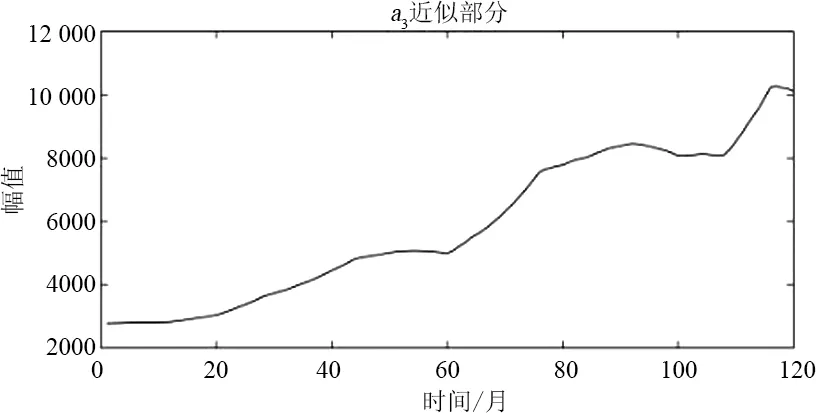
小波重构结果如图7所示,从图7可以看出,a3是近似分量也就是增长分量,代表着月售电量的增长特性,d1、d2和d3则为细节分量,也称为波动分量,代表着月售电量的随机波动特性。针对分解出的2组子序列的特点选择了2种适合的预测模型。下面对a3进行灰色模型预测,对d1、d3和d3使用ARIMA模型进行预测。
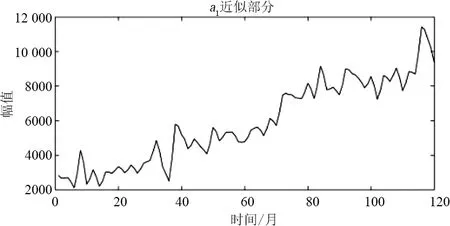
(a)

(b)

(c)
(d)
(e)
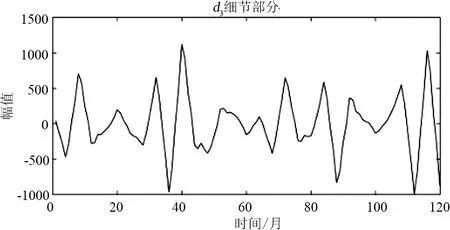
(f)图7 小波重构后恢复原始长度的各分量
4.2 灰色预测
从a3中提取出108个数据作为输入去进行预测,后12个作为结果进行预测分析,该灰色预测程序使用MATLAB来实现。预测结果如表4所示,结果比较如图8所示。
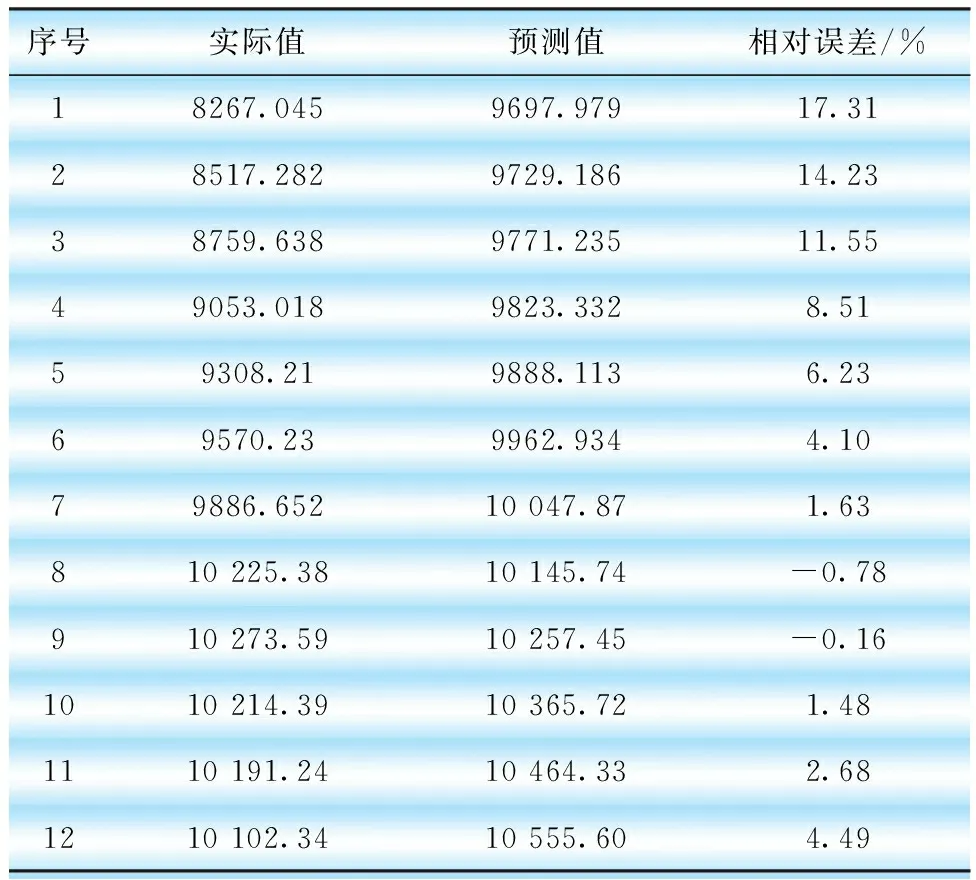
表4 近似分量a3预测结果
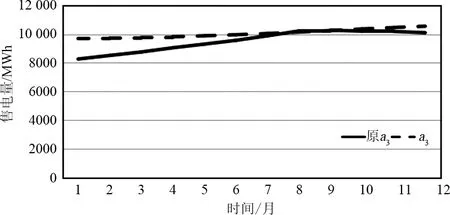
图8 近似分量a3预测结果与实际月售电量的比较
4.3 ARIMA预测
对细节分量d1、d2、d3进行ARIMA模型的预测,通过R语言软件实现预测模型的编程。针对这3个分量,使用3个不同的ARIMA(p,d,q)模型进行预测,并分别进行比较,使用tsdisplay(x)函数生成图像,结果如图9—图11所示。
从图9中可以看出有许多满足条件的模型,根据上文的介绍,通过计算AIC值,选择这个值最小的1个模型用来预测。使用auto.arima(x,trace=T)命令自动计算AIC值并进行比较,结果显示ARIMA(5,0,0)是最佳模型,AIC=1601.1。
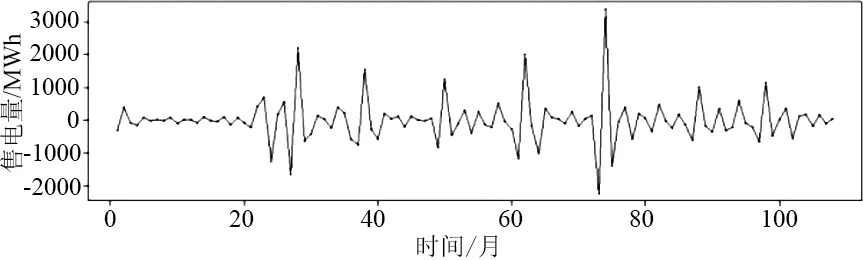
(a)

(b)
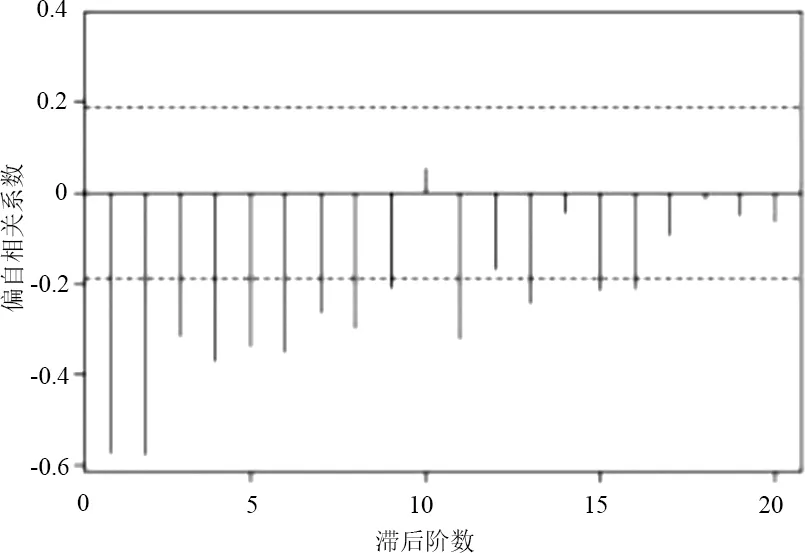
(c)图9 d1的ACF与PACF图
使用auto.arima(x,trace=T)命令自动计算AIC值并进行比较,图10结果显示ARIMA(4,0,0)是最佳模型,AIC=1445.92。

(a)

(b)
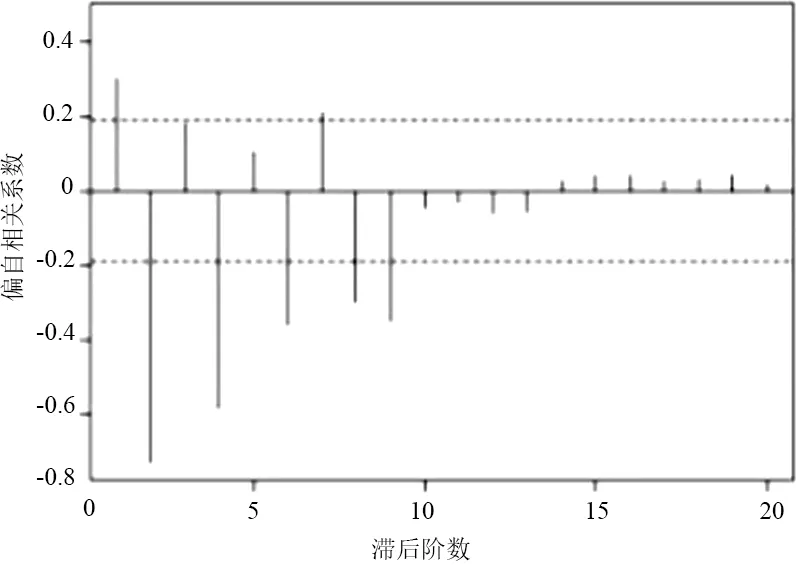
(c)图10 d2的ACF与PACF图
使用auto.arima(x,trace=T)命令自动计算AIC值并进行比较,图11结果显示ARIMA(5,0,0)是最佳模型,AIC=1370.07。
(a)
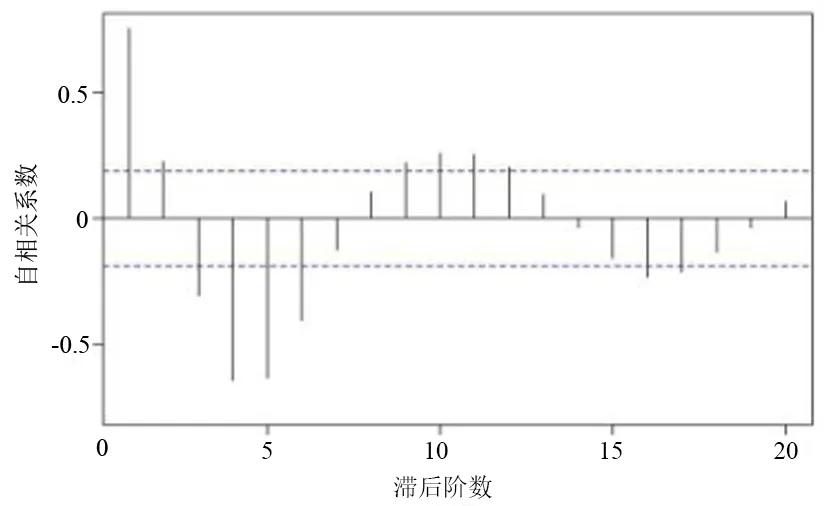
(b)

(c)图11 d3的ACF与PACF图
模型确定之后进行预测。为保证准确性,本文用1~108个月的月售电量去预测第109个月的月售电量,用2~109个月的月售电量去预测第110个月的月售电量。依此类推,每一个子序列进行12次计算得到下边的结果。预测的结果如表5—表7、图12—图14所示。
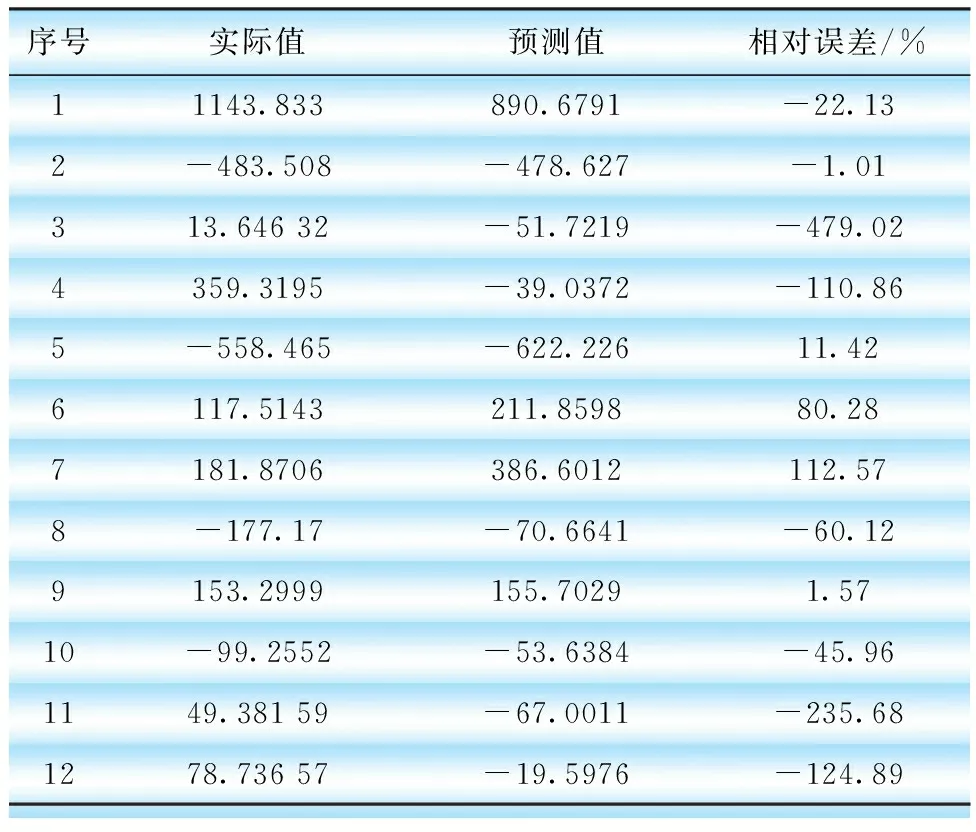
表5 细节分量d1预测结果ARIMA(5,0,0)
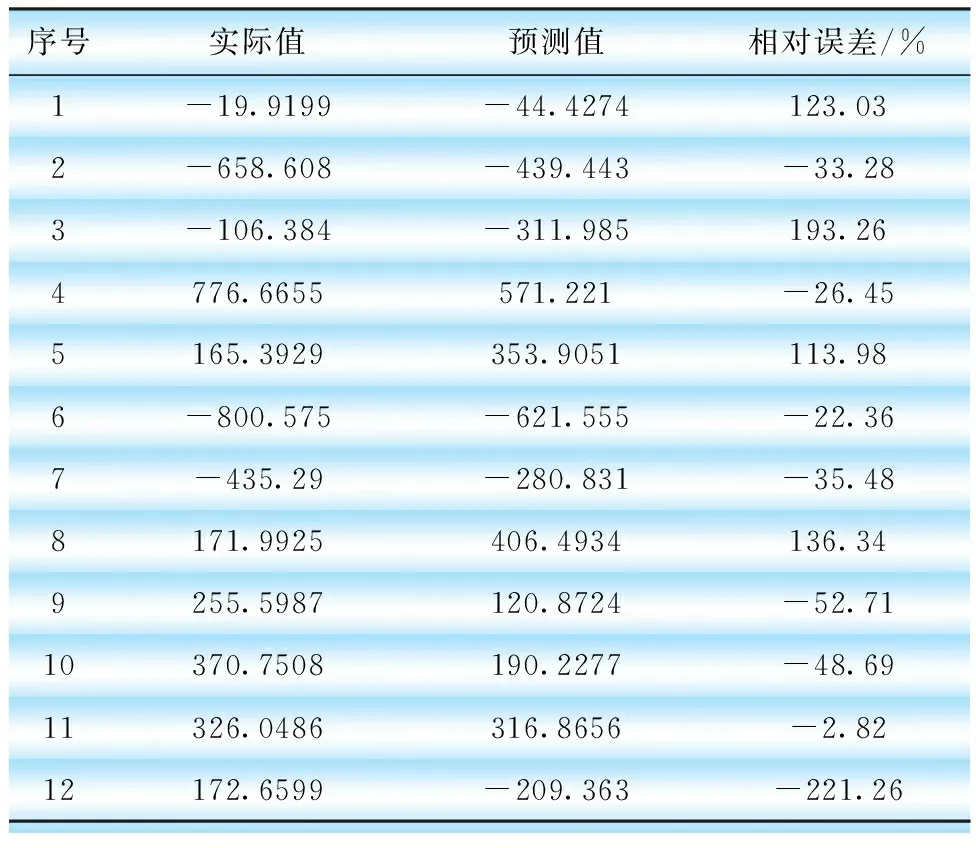
表6 细节分量d2预测结果ARIMA(4,0,0)
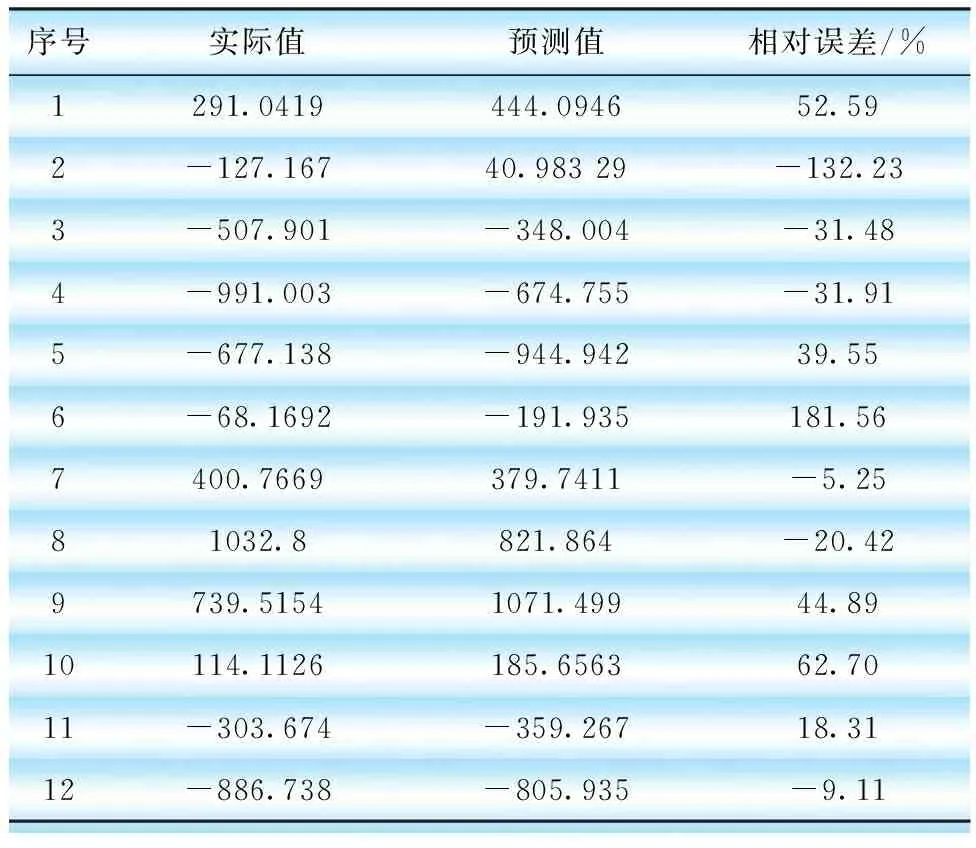
表7 细节分量d3预测结果ARIMA(5,0,0)
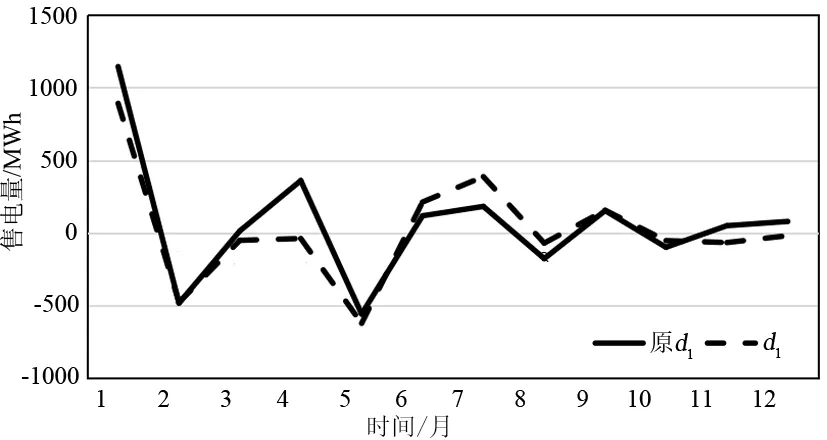
图12 细节分量d1预测结果与实际月售电量的比较

图13 细节分量d2预测结果与实际月售电量的比较
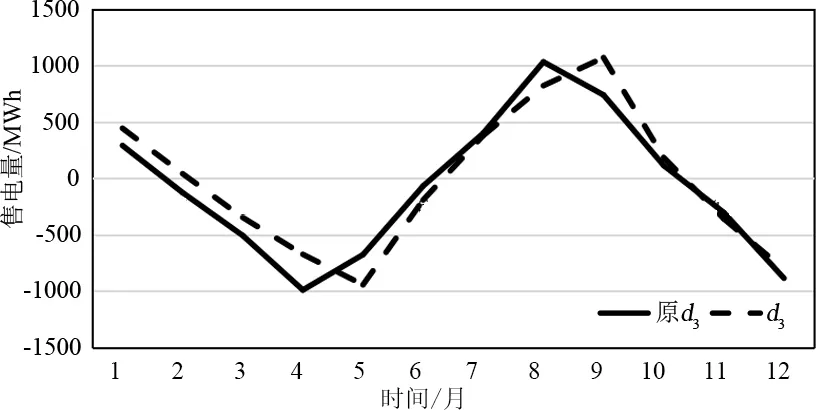
图14 细节分量d3预测结果与实际月售电量的比较
4.4 小波重构及误差分析
根据小波分解与重构,由式(1)可知,将预测出的4个结果直接进行相加运算就能得到最终预测结果,结果如图15、图16、表8—表10所示。

图15 负荷预测结果
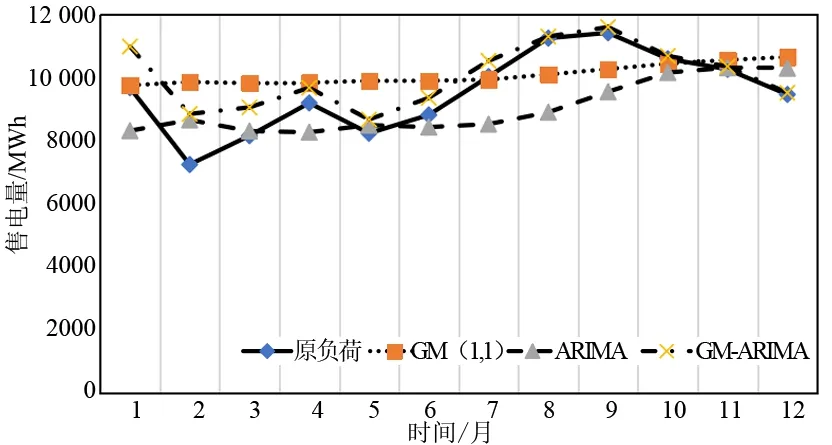
图16 各个预测模型结果比较

表8 预测结果
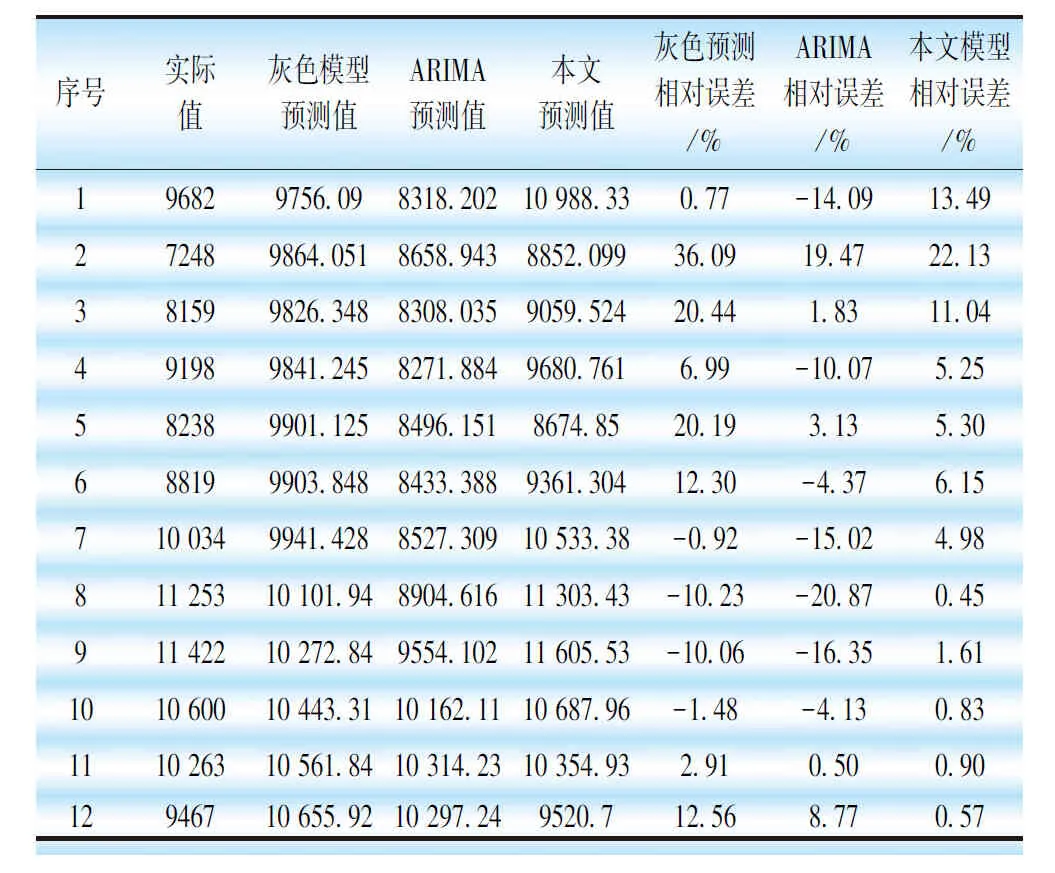
表9 本文方法与灰色或ARIMA单独预测比较
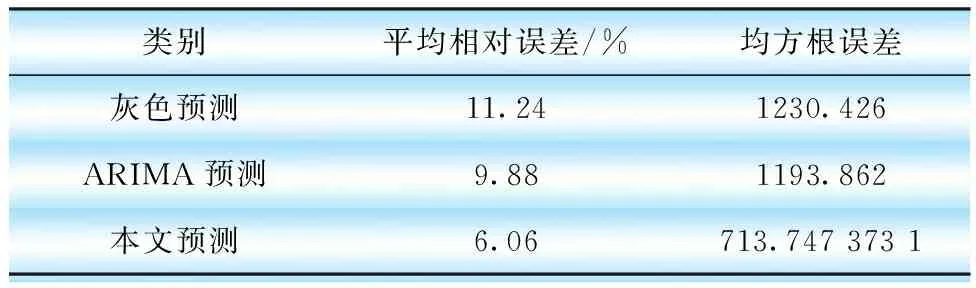
表10 本文方法与灰色或ARIMA单独预测比较
为了验证本文构建模型的精度,进行了实例仿真分析,通过前108个月售电量数据预测后12个月的月售电量,预测结果见表8,绘出预测结果曲线见图15。计算12个相对误差和平均相对误差见表9。误差分析结果显示,最大误差出现在2月,为22.13%,最小误差出现在8月,为0.45%,而平均相对误差为6.06%,低于10%,误差很小。为了进一步验证进行小波分析的有效性,使用灰色预测模型和ARIMA模型各自进行单独预测,并与本文模型进行比较,比较结果见表10和图16,结果显示灰色预测和ARIMA的最大误差分别为36.09%、-20.87%。最小误差分别为0.77%、0.50%,平均相对误差分别为11.24%、9.88%。
通过以上比较表明了本文提出的小波分析能够有效提高预测精度,并支撑售电公司制定合理的购售电策略,提高经济效益。
5 结语
本文首先介绍了月售电量预测的特点,重点介绍了国内外现有月售电量预测方法和研究现状,并分析探讨了这些方法的优缺点以及使用条件,在此基础上提出了一种基于小波分析的月售电量预测方法。小波分析并不是一种直接预测,而是一种分解重构思路,月售电量序列中同时具有逐月增长特征和随机波动特征,直接进行预测无法获得准确结果。通过小波分析将这2种特征分成具有单独的逐月增长特征子序列和随机波动特征子序列,然后再选取模型进行预测,最后将结果相加就会得到最终的预测结果。
本文成功编写出MATLAB小波分解与重构程序,能够对月售电量序列进行分解与重构;对增长特征子序列选取了灰色预测模型,通过编写MATLAB灰色预测程序,能够对增长特性的子序列进行预测;对随机波动特征子序列选取了时间序列-ARIMA预测模型,编写出R语言时间序列-ARIMA预测模型,能够对平稳波动子序列进行预测。
最后通过仿真并对其进行误差分析发现:对小波分解之后的预测结果与不进行小波分解而直接用这2种预测方法进行预测的结果比较,结果显示采用了小波分解这一过程之后预测的结果更为准确,误差更小,精度更高,表明了对月售电量序列进行小波分解之后再预测能有效提高预测精度,能够解决售电公司预测精度的问题。

