视频监控前端点位视场重合度计算方法研究
王昂千
(诸暨市公安局 浙江省诸暨市 311800)
1 概述
当视频监控摄像机的镜头光圈开至最大,并对准无限远景物调焦时,在成像靶面上呈现出的影像均位于一圆形面积内,而圆形以外则漆黑无影像。有影像的圆形面积称为该镜头的最大像场,在最大像场范围的中心部位,有能使无限远处的景物结成清晰影像的区域,这个区域称为清晰像场。摄像机成像靶面一般都位于清晰像场之内,这一限定范围称为有效像场。
当把镜头对准无限远调焦时,凡是通过镜头主轴的平面,必与有效像场的边缘相交于两点,从这两点引两条直线相交于镜头的像方主点,所形成的夹角被称为有效像角。由于有效像场通常是长方形或正方形,因此有效像角可归纳为三种,即水平像角、垂直像角和对角线像角。
像场所对应的景物范围被称为视场(Scene),凡通过镜头主轴的平面,从与视场边缘相交的两点引直线至物方主点,同样形成三种视角,即水平视角、垂直视角和对角线视角。
在视频监控系统建设中,作为前端感知设备的监控摄像机,需要根据实际监控场景需求,选择不同的摄像机、镜头、采用不同的安装角度以有效地监控某一区域,此区域即为该摄像机的视场。
两个相邻且具备同样功能需求的摄像机,有可能出现视场重合的情况,当两个摄像机的视场重合度(Scene Intersection)超过一定比例时,则表示摄像机的监控区域有重复,安装角度或监控选点可能存在问题。
两台摄像机的视场重合区域是一个三维空间区域,为了简化计算,本方法采用摄像机在水平面上投影所形成的区域,作为摄像机重合度计算指标。因此摄像机视场投影重合度(Scene Intersection Projection)可认为是两个摄像机的视场在水平面上各自投影,所形成两个平面多面体之间交集的面积,与各自摄像机投影面积的比例。
如图1中所示,摄像机CA在水平面上的投影为△ABC,摄像机CB在水平面上的投影为△DEF,△ABC与△DEF交集为多边形CGEH。多边形面积SCGEH/三角形SABC或者SDEF的值,即为CA与CB摄像机的视场投影重合度。

图1:CA、CB摄像机各自在水平面上的投影示例
2 摄像机视场投影
一台摄像机的视场,由其控制距离r、水平视场角α、垂直视场角β、安装角度θ、安装高度h所决定。其视场投影是摄像机视场在水平面上的投影所构成,如图2所示。
如图2所示,摄像机在水平面上的投影为一等腰梯形DEBC。AM为摄像机的主轴线,OM为摄像机的控制半径r,其中∠CAB为摄像机的水平视角α,∠KAN为摄像机的垂直视角β,∠OAK为摄像机的安装角度θ。
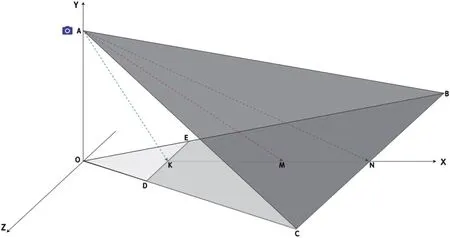
图2:摄像机在水平面上的实际投影
2.1 控制距离
不同的摄像机根据实际功能需求,具有不同的控制距离,该控制距离一般根据实际应用经验估算得到,并取决于监控摄像机所采用的成像靶面尺寸以及镜头焦距,不同的厂家有不同的设定。
2.2 摄像机视角
摄像机视场角包括水平方向上的水平视场角,以及垂直方向的视场角,同样取决于所采用的成像靶面尺寸以及镜头焦距,不同的镜头及摄像机,具有不同的视场角,如水平、垂直方向视场角。
2.3 摄像机视场投影
摄像机视场在垂直方向的投影,如图3所示。

图3:摄像机视场在垂直方向上的投影
其中AM为摄像机主轴线,摄像机安装高度为h,OM为摄像机控制半径r,摄像机安装角度为θ,摄像机垂直视场角为β。则有如下公式:


摄像机在水平方向上的投影如图4所示。
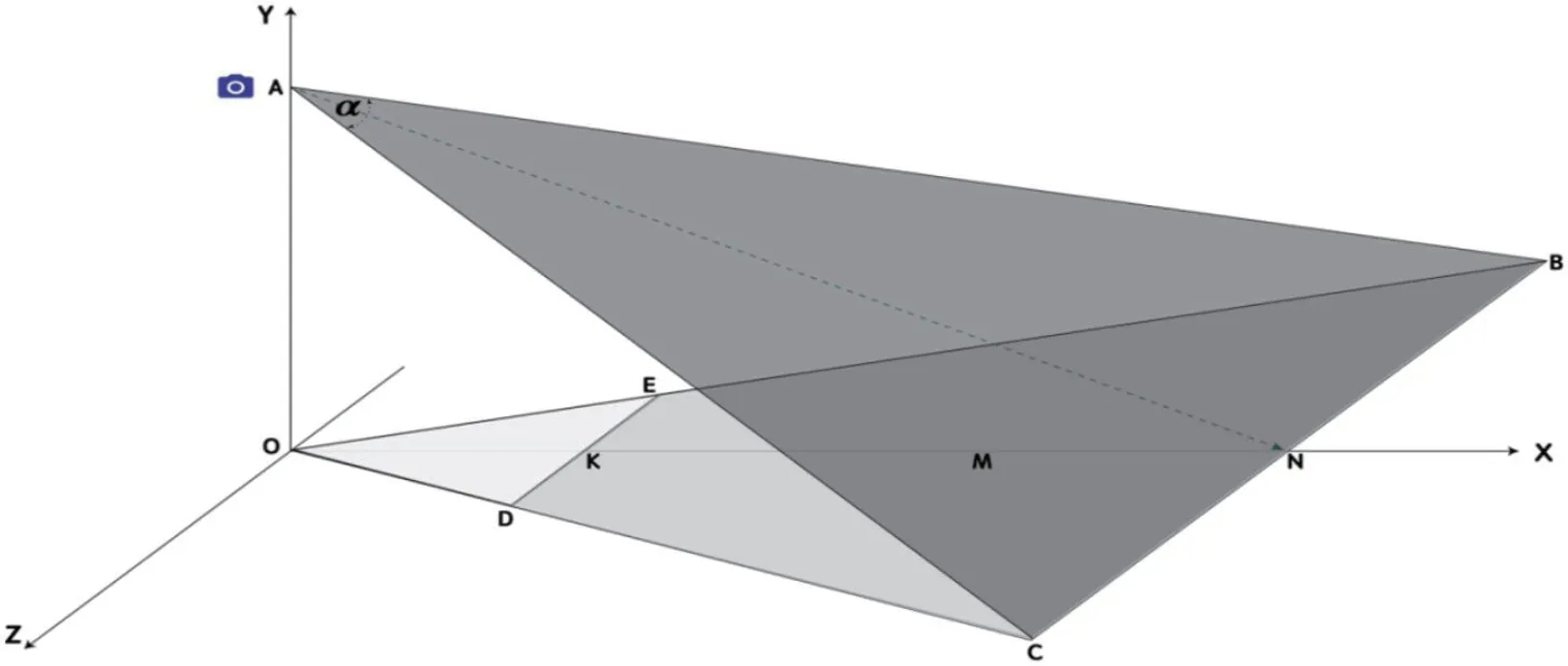
图4:摄像机视场在水平面上的投影
摄像机水平视场角为α,则根据公式(5),可得:
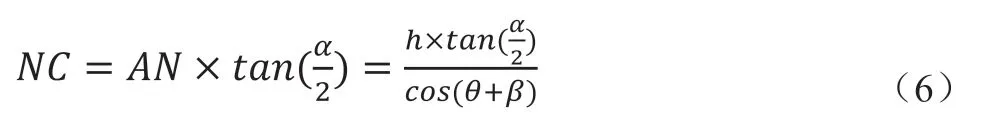
根据公式(2)、(3)以及(6),可得:

由上述公式可知,一台安装高度为h摄像机在水平面上的投影为一等腰梯形CDEB,相对于摄像机的四角坐标如图5所示。

图5:摄像机视场在水平面上投影的坐标
3 摄像机视场投影交集
计算两个摄像机CA、CB的视场投影重合度,首先以摄像机在水平面的投影点为原点,摄像机主轴在水平面的投影为X轴,建立各自的视场投影坐标系,并根据2.3节中的方法得到每个摄像机投影各自的四个顶点的坐标,分别设为A{a1,a2,a3,a4},B{b1,b2,b3,b4}。其中A、B分别为CA、CB摄像机的投影,其形状为一等腰梯形。如图6所示。

图6:摄像机CA、CB各自的投影坐标
3.1 统一坐标系
在计算CA、CB投影重合度时,需要在同一坐标系方可计算。本方法以CA摄像机坐标系为基准,通过对CB摄像机的坐标系进行平移、偏转,将CB摄像机的投影转换成以CA摄像机为基准的坐标系中。
3.1.1 平移
设R为地球半径,根据CA、CB摄像机的地理坐标(本方法采用WGS84),其中CA的经纬度为(CA.lng,CA.lat),CB的经纬度坐标为(CB.lng,CB.lat)。以CA坐标系为基准,则CB摄像机坐标系统平移量分别为:

经平移后,CB摄像机在CA摄像机坐标系统的坐标分别如下:
CB摄像机位于(δx,δy);
CB摄像机投影四个顶点坐标为{c1,c2,c3,c4}:
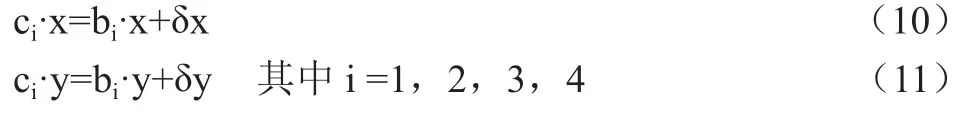
3.1.2 旋转
在实际应用中,CA、CB摄像机的轴线角度φ、φ是以大地坐标系统进行采集得到,如图7所示。

图7:CA、CB摄像机的主轴方向
CB摄像机的轴线方向与CA摄像机轴线方向往往是不同,两者之间存在一定的夹角φ,CB摄像机坐标系经平移后,须向CA方向旋转φ,才能将CB坐标统一至CA坐标系中。CB坐标旋转变换后的投影坐标为{d1,d2,d3,d4}:
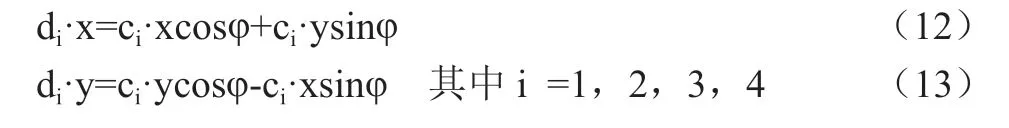
3.2 视场投影交集
经平移及旋转后,实现了CA、CB摄像机投影坐标基于CA摄像机坐标系统的统一,如图8所示。
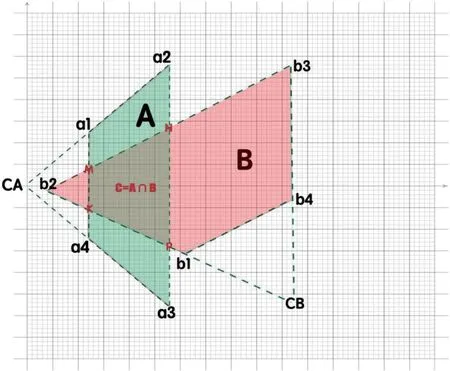
图8:CA、CB摄像机投影在CA坐标系中的交集
CA、CB摄像机在CA坐标系中,其交集为一凸多边形MNPK。摄像机CA投影为一等腰梯形A,其四个顶点坐标分别为{a1,a2,a3,a4},摄像机CB投影同样为一等腰梯形B,其四个顶点坐标分别{d1,d2,d3,d4}。
3.3 投影交集顶点坐标
显然,A、B两个投影的交集为C,要计算投影重合度,首先需要确定C的顶点坐标,而后计算C的面积。
交集C的顶点应该出自下面的两类点:
(1)A或B的顶点;
(2)A、B的边的交点。
第一类点的求法:显然如果一个梯形的某个顶点在另一个梯形内(包括在边上)则该顶点是交集的一个顶点,因此我们只需依次对两个梯形A、B的顶点进行判断,检验其是否包含在另一个梯形中,即可求出第一类点。本方法利用待判断点与另一个梯形的全部边按顺序组成的三角形的面积总和与此梯形的面积进行大小比较,来判断该点的归属,若大则在该梯形的外部,不属于第一类点;否则,是交集C的顶点。
第二类点的求法:两个梯形相交可能有两条边重合(包括部分重合)的情况,显然重合的部分必是交集的一条边,这条边的顶点是已知两个多边形的顶点,即应属于第一类点,在第一类点的求法中显然已包括了这种顶点,因此我们在求A、B两个梯形的边的交点时,可以不计算两条边重合时的交点,而只计算两条边相交〔不平行〕时的交点。在本程序的算法中为了求两条边的交点,我们采用线段的参数方程表示法,即:
x=a*t+b
x=c*t+d 其中0<=t<=1;
设线段的两个端点坐标分别是(x0,x0)和(y1,y1),则线段的参数方程可写成:
x=(x1-x0)*t+x0
y=(y1-y0)*t+y0 其中 0<=t<=1;
据此可以求两条边的交点。
3.4 投影交集面积计算
如果某个梯形的顶点在另一个梯形的边上,由上面的算法可知它将被分别计入两类点当中,因此我们最后求得的交集C的顶点可能有部分是重复的,但由多边形的面积算法可知这不会影响面积的大小,因此在确定两类点时,不需要做精细的划分。
当得到交集C的顶点坐标后,按照各顶点的X坐标大小排序,再根据Y坐标大小排序,从而得到一个有向多边形,如图8中所示,交集C的顶点为M、N、P、K,将该多边形切分成三角形,如图9所示。
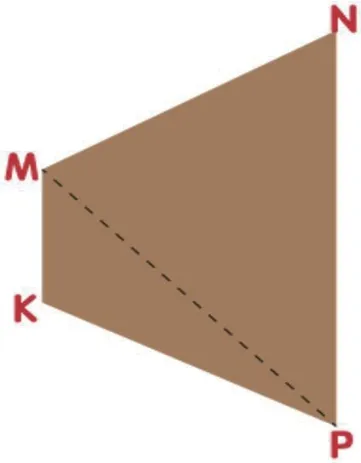
图9:摄像机投影A、B的交集C
如图9,摄像机投影的交集C可划分成两个有向三角形△MNP和△PKM,C的面积可Sc=S△+S△得到。而三角形的面积可以有海伦公式得到。
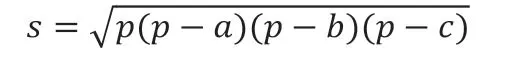
其中a、b、c分别为三角形三条边长,p =(a+b+c)/ 2。
4 摄像机视场重合度计算
计算两个摄像机CA、CB的视场投影重合度,需分别计算摄像机投影A、B的交集C的面积与A、B面积之比,得到投影重合度r、r。当r或r超过预设的阈值时,则表示这两个摄像机重合度过高。

