信道化接收机瞬时测频比相算法

刘煊赫 林坤东 魏一鸣 王郡

（1.南京理工大学电子工程与光电技术学院 江苏省南京市 210094）

（2.南京理工大学中法工程师学院 江苏省南京市 210094）

1 引言

宽带信道化数字接收机的快速测频技术应运而生，采用信道化接收机能够处理同时到达的多个信号并有较高的截获概率，采用多相滤波信道化接收机运算量小并易于实现，为了克服D倍抽取而产生的接收盲区，提高测频精度，引入了重叠一半的多相滤波信道化数字接收机，并采用了瞬时自相关接收机，以达到预期目标。其中顺时测频技术的支撑尤为重要。实现快速测频主要有两种不同的路径。第一种是对输入信号进行数字采样，将其变为数字信号，再通过处理获得输入信号的频率。除对信号进行数字处理外，应用较多的是将信号频率进行相位变化，再进行幅度变化，通过对信号幅度测量获得频率信息，既普遍使用的干涉比相法。基于CORDIC算法容易得到相位信息，便于进行接收机滤波器设计实现接收机信道化划分，模拟信号处理方法探究瞬时测频精度影响因素。

2 瞬时测频核心方法

实现瞬时测频主要有两个核心思路，其一是数字信号处理方法，通过对输入信号进行数字采样转变为数字信号，从数字信号中获取频率信息；另一种是模拟信号处理方法，通过测量信号的幅度信息，反解出相位信息进而得到信号频率。

接收机获取信号首先经过采样处理，只需进行相应的傅里叶变换、相位推算以及频率推算就可以的到信号的频率信息。同时，傅里叶变换法适用于单频信号，测频结果容易得出，常用于信号的初步频谱分析。由于傅里叶变换法测量精度由采样点数量决定，因此在提高精度方面只需对信号在峰值处插值，并不影响信号信息的完整性。相对于频率推算要求采样点数量较少，相位推算法更容易实行，不需要太高的量化运算可以的大大降低运算时间，瞬时性较高。

瞬时测频模拟方法较多，通常有鉴频法、驻波鉴相法以及多信道划分法，以下讨论主要以多信道划分法为主。鉴频法输出的幅度编码信息与输入频率相对应，可以近似将频率与输出结果做函数对应关系进而求解信号频率，这种方法虽然简单但测频精度较低。而鉴相法是利用传输线驻波特性，根据驻波的幅度信息确定信号频率。由于传输线限制，这种方法仅限于窄带信号。

多信道划分法核心思想是通过多个分频器划分事先规定的固定信道，经过比较电路输出结果判断信号通过哪一信道，从而确定其频率。在实际操作中通常要满足划分的信道足够小来提升测频精度。其关键技术在分频器，分频器单输入多输出且每个输出端口对应一定范围的频率段，能够将输入信号频率转化为0—1组合的幅度信息。

3 干涉仪比相法

3.1 干涉仪比相法原理

干涉仪比相法瞬时测频原理同之前所述模拟方法，将测频任务转变为测相位信息。要想获得相位信号就需要获得同一信号的相位差，可以通过相位延迟器实现，也可利用传输线的传输特性获得相位差，如图1。

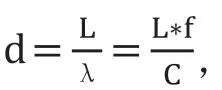
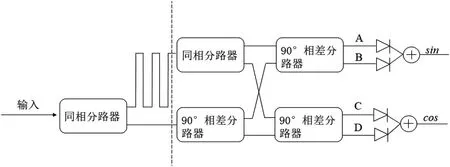
图1：干涉仪比相法原理图

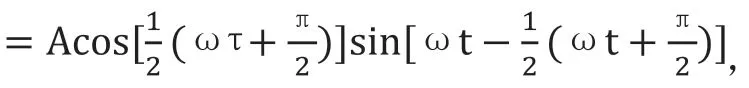
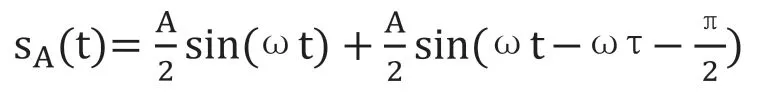
经过检波以及滤波后输出信号为s=kAsin(ωτ)、s=kAcos(ωτ)

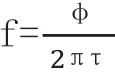
干涉仪比相测频方法的主要优点有硬件结构简单，工作原理并不复杂。但其缺点是测频精度不高，延迟线设计只满足输入信号中心频率的要求，若延迟线和中心频率未匹配，则测频精度将急剧下降。

3.2 CORDIC相位提取

目前，典型的CORDIC算法实现结构有两种，迭代结构与流水线结构。迭代结构方法是根据CORDIC算法方程直接实现；流水线结构方法将结合流水线结构特点与迭代方法实现。

迭代方法的工作流程，首先数据输入到x，y两个寄存器中，然后每个寄存器里的数据分两路输出，一路到位移器里，一路到加法器里，和从来自另一路位移器（位移器位移次数随迭代次数增加而增加）里的数据进行加减运算，然后送回原寄存器当中。然后Z寄存器中的数据则直接送回加法器中，与来自查表中的数据进行运算，随着迭代次数增加，查表的地址也增加。但必须有一个状态机来跟踪迭代过程，控制位移器深度、查找表地址和决定符号因子。这必然导致运算效率低下，运算速度慢。

根据CORDIC算法原理图，如何确定信号的相位信息是干涉仪比相算法实现的核心。相位信息提取方法有很多，常用的方法有模拟的环形电阻网络和数字的CORDIC。环形电阻网络结构简单，运算速度快，但是很难满足我们所要求的精度。CORDIC算法通过基本运算实现复杂乘法运算，节省大量硬件资源，所以使用CORDIC算法实现相位信息提取。

CORDIC算法坐标平面旋转图如图2所示。CORDIC算法通过用固定角度进行旋转逼近设定角度来实现复杂运算，属于逼近过程，以下是CORDIC算法基本原理说明：

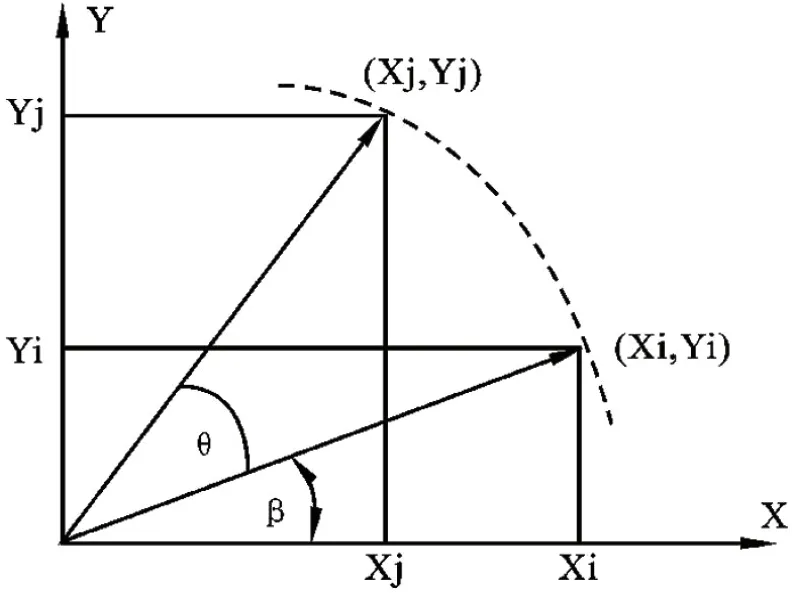
图2：CORDIC算法坐标平面旋转图

从(Xi,Yi)旋转θ到（Xj,Yj），cosθ是确定，故暂不做考虑，得到坐标变化方程：X=Xcosθ-Ysinθ=(X-Ytanθ)cosθ

Y=Ycosθ+Xsinθ=(Y+Xtanθ)cosθ

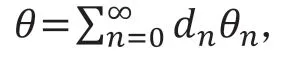
而且随迭代运算次数加深，聚焦常数K是(arctan(2))的趋近值，经过八次迭代运算后，K趋近于0.60725。

以上介绍了CORDIC算法的原理以及聚焦常数的验证，从上述的分析过程中可以看出利用复杂的反三角函数运算求相位被化简为移位运算和加法运算，使信号处理速度加快，硬件资源利用更加高效。CORDIC算法在实际应用中已经是一种成熟的方法。

4 信道化接收机

4.1 信道化接收机仿真

在收到一个信号后，首先要通过接收机进行处理，因此在测频功能仿真之前进行了信道化接收机的仿真。选取信道带宽为0～1GHz，并将其16等分，故每一个小的信道宽度为62.5MHz。编写程序时，可以将每一个小信道等效为截止频率为31.25MHz的低通滤波器，用低通滤波器作为衡量标准进行信道划分。

在MATLAB窗中输入“filterDesgner”调出滤波器设计工具界面，依次选择低通，FIR，窗，Hamming，低通滤波器阶数N设为512，截止频率Fc设为31.25MHz，采样频率Fs设为1GHz，设计一个低通滤波器。将其抽头系数保存在“.mat”文件中，为后续使用做准备。

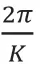
在偶排列中，第k个信道中心频率为：

在奇排列中，第k个信道中心频率为：

我们选择偶排列编程，接下来我们输入一个频率为356.5MHz的单频正弦波信号，让信号通过信道化接收机，然后将接收到信号的信道频谱图输出，观察其正确性。

由于每个小信道的中心频率为62.5MHz，可以求出第六信道的频率范围为343.75.MHz～406.25MHz。结果输入频率为356.5MHz的单频正弦波信号存在于第六信道，模拟程序的正确性得以验证。

输入信号在进入到接收机后，需要对其存在哪一个信道进行判断。因为在实际工程中我们无法得知输入信号的初始频率，所以我们可以利用信道化接收机来初步判定输入信号的频率大致存在范围，以便后续对信号处理是否准确做出比较。在此，利用信号能量远比噪声能量大的特点进行编程，设定判决门限，对每一个信道进行对比，直到找到信号存在的信道，再输出结果，然后提取出输入信号送到瞬时测频系统中进行处理，最终测频结果为354.2MHz。

4.2 分析影响信道化接收机的因素

4.2.1 低通滤波器过渡带的影响

一个低通滤波器幅频特性曲线可以大致分为三部分：通带、过渡带、阻带。在理想情况下低通滤波器的过渡带宽度应为零，在这样设计的信道化接收才会达到最佳状态，但在实际工程中低通滤波器的过渡带宽度永远不可能为零，因此在使用低通滤波器进行信道划分时，会产生过渡带叠加的情况。

当输入信号频率正好落在两个信道过渡带的叠加处时，则会造成信道判决失真，输出结果为两个信道均存在信号，甚至多个信道，那么此时的结果失去了初步判断输入信号频率范围的作用。下面进行仿真并对其结果进行观察，输入信号频率为343.75MHz，信噪比为10dB，在第5、6信道均存在信号，最后经过信道判决输出结果也为输入信号存在于第5、6信道。所以当输入信号落在过渡带交叠处时对结果会造成巨大影响。

4.2.2 输入信噪比的影响

在实际工程中，输入信号永远伴随着噪声一起被接收机接收处理，当信噪比过小时，信号能量较小而噪声能量较大，信号能量无法到达接收机判决门限，而将噪声当作信号；当信噪比过大时，在相邻信道的输入信号旁瓣能量可能达到判决门限，会输出多个结果造成失真。所以当信噪比过大或者过小很可能影响接收机最终的输出结果，下面通过仿真结果进行验证，仿真结果如表1所示。

表1：输入频率为450MHz，信噪比不同的信号的仿真结果

从表1中可以看出，判决门限的设定决定了接收机的输入信噪比范围。输入信号信噪比小于-10dB时，由于输入信号能量太小，未达到接收机门限，接收机无法进行判决；当输入信号信噪比大于20dB时，由于输入信号旁瓣能量太大，导致相邻的第六、八信道均被判为存在信号，导致结果失真。六、八信道出现信号的原因是信道化接收机中构成其他信道低通滤波器的阻带延伸到信号所在的信道，信号通过之后会产生旁瓣，因此这里会产生旁瓣干扰。所以，在实际应用时我们应根据实际情况进行门限的设定。

4.3 瞬时测频

4.3.1 瞬时测频仿真

输入信号经过信道化接收机处理后，将输入信号提取存储，随后送入到瞬时测频系统中。

对其进行时延，时延时间为0.5μs，信号经过0.5μs延迟后，信号的频率信息已经转化到相位信息，相位信息对应为0.5μs内上下两个信号相差多少个2π相位。这里我们利用MATLAB函数库中findpeaks函确定好起点和终点，计算出两个信号的相位差，再经过准确计算得出输入信号的频率。下面通过仿真结果来验证瞬时测频系统的正确性，仿真结果如表2所示。

表2：干涉仪比相法瞬时测频仿真数据

我们在输入信噪比不变的情况下，改变10次输入信号的频率并进行仿真。可以从数据中看出输出的测量值有一定的误差，但误差都在可以接受的范围内，而且通过仿真我们找到瞬时测频系统的测量范围为6MHz～1GHz，测量精度为2MHz。

测量范围和测量精度是测频系统中两个重要的指标，在上面我们通过仿真测量的方法得到了这两个指标的数值，下面我们通过对算法的分析来确定这两个指标数值的正确性。信号经过时延后，利用find(x, x, ‘first’)函数确定起点与终点，再利用findpeaks函数计算相差的相位。在测频的过程中对输入信号的采样生成的数据的总数是确定的，所以当输入信号频率较高时，每一个2π周期中采样的数据点较少，那么利用find函数很容易确定起点和终点；但当输入信号的频率较低时，每一个2π周期中采样点的数据点较多，就会存在很多幅度相近的数据点，那么利用find函数就不容易确定起点和终点，延时前和延时后的起点终点不同，就会造成测量频率失真。所以，瞬时测频系统在0～6MHz失真严重无法测频。

频率计算部分我们直接利用findpeaks函数测量延时前和延时后的信号相差多少个2π周期，然后再除以0.5μs（因为信号时延为0.5μs）得到了测量频率，所以测频精度2MHz。如果我们想进一步是测频精度扩大，那么就要精确求出在0.5μs内的相位差为多少，求出的相位差越精确，则测频精度也就越高。