一种多级特征辅助的精密测速方法

周明阳 蔡玖良

（中国电子科技集团公司第十四研究所 江苏省南京市 210039）

1 引言

单脉冲测量雷达通过提取目标回波的多普勒频率得到目标速度，得益于雷达频谱纯度与相参技术的提高，在目标探测场景理想的情况下可以获得较高的测量精度。目前的目标测速方法一般采用闭环测量法，用窄带跟踪滤波器和二阶环路实现，在此基础上，针对多普勒频率捕获与跟踪之初，对跟踪频谱可能出现的多普勒频率模糊，利用测距数据微分得到的速度与测速数据相比较，平滑处理后估计模糊谱线数，进行速度消模糊。

在实际目标跟踪过程中，回波相位常因目标起伏导致相位质量下降，多散射点噪声、目标震动、信号遮挡等不利因素都可能导致测频误差甚至出现跳谱线，上述方法不能很好的适应这类复杂场景。

本文设计了一套精密测速流程，利用滑窗傅里叶变换进行速度测量，利用惯性滤波器进行滤波跟踪，精密测速；针对在多散射点、目标起伏等复杂场景下跳谱线问题，设计了一种完备的实时滑窗模糊纠正方法，利用点迹距离、信噪比、距离差拟合斜率、拟合系数等特征作为辅助，排除干扰，准确判断并估计速度模糊度。通过该方法可得到稳定可靠的速度信息。

2 闭环测速与速度跟踪系统

雷达采用单脉冲跟踪工作方式，每个驻留只包含单个脉冲，采用线性调频信号，利用多个驻留回波数据进行频率测量与测速。

设第n 个驻留发射脉冲波形为：

其中，A为回波幅度， 为回波时延，c 为光速，λ 为波长。则脉压后的回波为：

如果考虑目标加速度，回波频谱展宽，影响速度测量，需要先对加速度进行跟踪估计，使用加速度对回波进行展宽修正，再进行速度测量。加速度跟踪方法与速度相似，首先利用分数阶傅里叶变换、Wigner-Ville 分布等时频分析方法获得本次滑窗估计的目标加速度，再使用上述一阶惯性滤波器进行跟踪滤波。也可以根据速度测量偏差使用α-β 滤波器组成二阶速度跟踪环路，同步进行速度、加速度跟踪。

3 全程跳谱监测

考虑到初始目标速度误差可能跨多普勒，导致每帧速度跟踪结果与真实速度相差整数倍个Fλ/2，可以利用闭环测速积分与雷达测距距离的差值进行跳谱检测并纠正。另外，对于相位质量较差的复杂场景，在其跟踪过程中也可能出现跳谱现象，需要进行全程监测，且监测机制本身也需要剔除多散射点干扰、目标起伏、测距误差等影响。在此设计了全程的实时跳谱监测与纠正流程，准确得到测速误差，进行速度纠正。流程的关键点有：

3.1 点迹距离与滤波器预测距离比较

预测距离由雷达目标跟踪滤波器得到，在对上一帧数据进行滤波时产生。在信噪比较低时，滤波器产生速度、加速度的误差会造成预测距离的偏差，且具有一定的时间相关性，导致预测距离的偏差产生积累，积累偏差较大时会影响对测速误差的监测；点迹距离由回波检测后凝聚得到，与滤波预测距离相比，虽随机差较大，但时间相关性弱，不存在积累偏差。所以本方法使用点迹距离进行速度模糊估计。

3.2 “测速积分距离-点迹距离”差值曲线拟合斜率与拟合系数

测速无模糊时，测速积分距离与点迹距离差值所得直线斜率为0；而当出现模糊且模糊度为M 时，差值斜率为M倍的模糊速度。利用“差值斜率为模糊速度的整数倍”作为先验信息对拟合斜率与模糊速度的关系进行限制，可以有效提高速度模糊的识别准确性。

另外，若距离差值出现波动或异常值时，会造成模糊度估计偏差。利用拟合系数约束可以有效避免此问题：当拟合系数低于某一门限时，判断此次距离差值线性度差，斜率估计值可靠性差，不使用此次估计斜率纠模糊。

3.3 信噪比过低判断

在信噪比较低甚至在目标所在距离单元无检测点时，都可能引起距离差拟合窗中出现异常点，导致斜率估计错误或得到的拟合系数过低。而对于信噪比起伏大的目标，这种情况发生频繁，影响模糊纠正。

本方法在设置距离差值窗的同时，设置了低信噪比标识窗，对于检测信号幅度低于某一门限或者未检测到目标的数据帧，在纠模糊判断时被丢弃，不参与距离差值窗的线性拟合，减少过低信噪比异常点的影响。

跳谱监测的流程设计如图1。

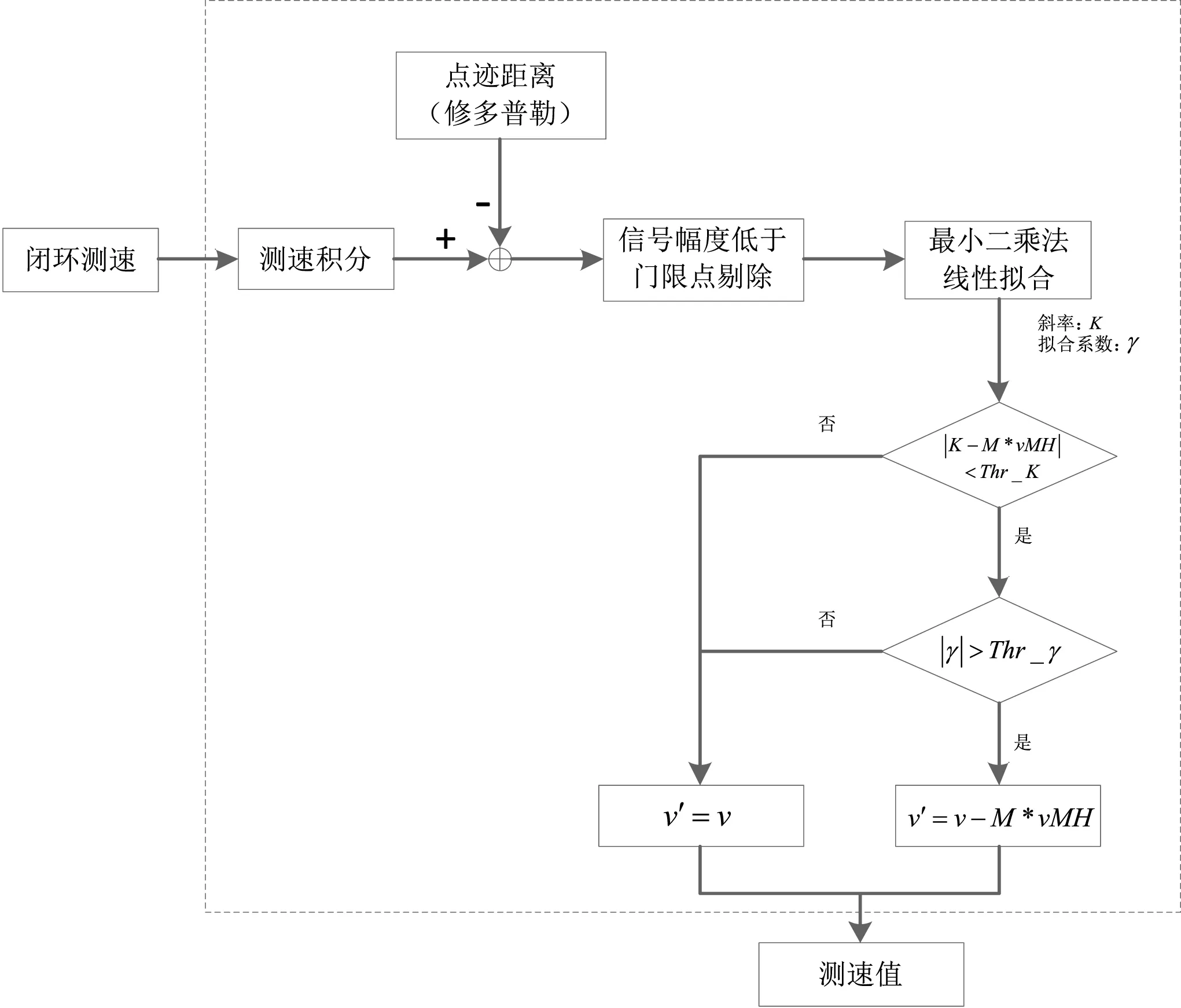
图1： 跳谱监测流程框图

具体步骤如下：

（1）对闭环测速值持续积分；

网络课堂的课程选择也可以不局限于学生本专业的专业选修课，特别是需要在课堂内容中引进国学、音乐、科技方面的课程，使学生在学习理论的同时进行深层的知识拓展，在知识拓展的过程中拥有高方向的个人视野。

（2）计算目标点迹距离，并完成多普勒距离修正；

（3）滑窗记录测速积分与点迹距离的差值以进行全程速度模糊监测；

（4）计算纠模糊窗内信号幅度，低于门限点进行剔除；

（5）窗内剩余点利用最小二乘法完成线性拟合，计算得到拟合直线斜率K 与拟合系数γ；

（6）比较斜率与速度模糊值，若斜率与速度模糊值的整数倍偏差小于门限Thr_k，则满足斜率要求，继续下一级判断，否则，判断无模糊；

（7）判断拟合系数是否大于门限Thr_γ，若大于则认为线性度满足，可以进行模糊度计算，否则，判断无模糊；

（8）根据判断结果进行纠模糊处理，v'为最终测速值。

4 仿真分析

利用本文测速方法对某雷达探测目标所记录回波数据进行仿真处理，完成功能验证。试验中选择非球形星作为探测目标，其回波起伏较大，多散射点互相干扰，可以验证本方法的处理效果。试验中卫星从远处进入雷达探测范围，过捷径后离开。

图2： 本文方法测速效果

截取有速度模糊的一段数据展示低信噪比对“测速积分距离-点迹距离”差值产生的影响以及本文方法针对性处理的效果。

如图3 所示，若对此段距离差值曲线直接进行线性拟合，拟合效果见图3(a)，图3(b)为相应时间段的目标回波幅度。图3(a)中可见在0.4s 左右出现多个异常点，此段与图3(b)中回波幅度较低处（噪底约为30dB，被噪声污染严重）相对应；从拟合斜率可以判断此处出现了速度模糊，但由于拟合直线斜率为模糊速度的1.49 倍（非整数倍），且拟合系数仅为0.08，无法准确识别模糊度。

图3： 低信噪比对距离差值拟合产生的影响

按照本文方法，设置低信噪比标识窗，依照信号幅度与门限大小关系置标识位，低信噪比异常点不参与距离差值窗的线性拟合。去掉异常数据帧后再进行拟合，所得拟合斜率为模糊速度的1.09 倍，拟合系数高达0.8，如图4 所示。

图4： 去掉低信噪比异常点后的拟合效果

由于此时计算出的拟合斜率可信度较高，可更准确地估计速度模糊度，及时纠正模糊，保证测速稳定度与精度。

5 结论

本文设计了一种精密测速方法，利用滑窗傅里叶变换进行速度估计，利用一阶惯性滤波器进行跟踪滤波，可以得到较高精度测速值；针对多散射点、目标起伏等复杂场景下可能出现的多普勒模糊问题，设计了一种完备的实时模糊纠正方法，利用点迹距离、信噪比、距离差拟合斜率、拟合系数等作为辅助特征，排除干扰，准确判断并估计速度模糊，保证了测速稳定度与精度。利用实测数据验证了方法的有效性。