浅谈高职数学教学中学生数学思维的培养

黄琪芳 霍思明

[摘           要]  随着教育改革的持续深化，现阶段的教育教学更加注重学生综合素质的发展。数学是贯穿整个教育阶段的重要科目，其产生的教育影响是重大的，加之高职作为社会发展中技术型人才培养的主要基地，其教学质量对学生以及社会的发展都有着非常积极的促进作用。因此，注重高职数学教学优化是必要的。针对这一主题进行细致的分析和论述，以供参考。

[关    键   词]  高职学生;数学思维;培养策略

[中图分类号]  G715                    [文献标志码]  A                  [文章编号]  2096-0603（2022）24-0115-03

整体而言，现阶段的高职数学教学质量相较于以往有很大的提升，学生的学习水准也有了很大的进步。但是结合社会发展对高素质人才的需要来看，学生的培养实际与理想的培养目标仍存在一定的差距，其主要体现在学生的数学思维培养不足。结合实际的教学能够发现，高职数学教学中存在不关注学生思维建设以及学生思维建设受到多种因素阻碍的现象，学生的数学素养始终得不到有效的培养和提升。本文以此为例，通过三个方面进行分析论述。

一、学生数学思维的相关论述

（一）具体内涵

所谓思维即指人的大脑对客观事物的本质以及内在规律的一种概括、间接的反映。相较之下，数学思维较为特殊，其主要是指人的大脑运用数学符号与数学语言间接、直接反映数学对象的过程，是以数学概念为基础，运用相应的判断与推理方法，认识数学对象的本质的过程[1]。

（二）主要类型

结合教学实际，通过对相应的数学思维进行归纳能够发现主要包含以下四种。

1.归纳思维

这一思维是指学生在学习中通过自身对知识的探究、观察以及理解，总结归纳出数学知识的具体内涵。注重这一思维的培养，不但能够帮助学生形成融会贯通的能力，还能在一定程度上培养学生的创新能力，使其能够在学习中认识到数学知识的具体作用和价值，借此提升学生实践运用知识的能力。

2.类比思维

这一思维是指学生在学习中借助两种不同性质事物间的相似性，通过将一种已经获得并理解的知识转移到新的事物中的推理方式，即两个对象存在一致性或者同构关系，或者在一对多的同态关系中对两个对象系统进行类比。在这一思维的培养中，学生的思维能够得到拓展和深化，由此发现数学学习中的奥妙，有利于提升数学学习实效。

3.创造思维

这一思维是指学生在学习中突破原本思维的限制和束缚，在探究中重新组合既有的知识经验和新信息，遵循一定的规律，得出新的、多维的、独特的思维结果[2]。在此过程中，不但能够强化学生对已有知识的理解和掌握，而且還能够借此拓展学生的其他学习思维，对其后期的发展进步有非常积极的促进作用。

4.逆向思维

所谓的逆向思维是指学生从事物的对立面、反方向思考，对传统经验或者已经成定论的、司空见惯的事物或者观点进行深入的论证、探究。在此过程中，学生的思维能够改变僵化、刻板、循规蹈矩的认识模式，在结合原有经验的基础上，对常识、惯例、公认的做法提出疑义和不同见解，使数学学习充满创造性和挑战性。具体在高职数学学习中，很多知识都可以借助这一思维对课本上的很多理论进行论证、探究，从而获得不一样的数学学习体验，逐渐培养求新求异思维。

二、高职数学教学中学生数学思维培养面临的困境

（一）教学理念较为滞后

通过观察实际教学能够发现，由于专业科目的设置，学生学习数学的时间较少，部分教师为提升学生的数学学习实效，多会出现细致讲解知识的现象[3]。产生这一现象的主要原因与高职数学难度较大有关，即高职数学中涉及的知识内容较多，并且具有一定的学习难度，为保障学生能够快速、有效了解、掌握，教师多会在教学中对所学知识进行细化讲解。虽然学生在教师的反复讲解或者题海战术中掌握了相应的知识和一定的方法，但长期如此对知识的理解以及运用始终停留在简单地照搬公式解题的层面，被动学习、机械学习的现象愈演愈烈，不仅无法实现教育目标，数学思维的培养更是无从谈起。

（二）教学课堂模式固化

课堂教学的有效性以及丰富性能够直接影响学生的学习实效。因此，注重教学课堂模式的优化是很有必要的。但是结合高职数学教学能够发现，教师在教学中仍旧采用教师主讲、学生听讲的模式，教学课堂模式固化，无法适应学生的实际发展需要。而且在这样的教学模式下，学生对数学学习的抵触或者其他不良学习心理会加剧，造成整个教学课堂质量低下，不利于学生的长远发展和进步[4]。另外，在固化的学习模式中，学生与教师之间的互动交流机会和时间较少，即使有也更多地倾向于基础较好且能够主动探究提问的学生，基础较差且兴趣薄弱的学生的交流非常少甚至没有。这样班级将会出现两极分化的现象，对提升教学实效会产生不良影响。也就是说，固化的课堂模式不仅不能很好地调动学生对数学知识的探究兴趣，而且数学思维得不到培养和锻炼，也会对学生后期的学习和未来进入社会开展工作产生负面影响。

（三）理论和实践联系不紧密

数学知识有很强的实用性，特别是进入高职阶段后，数学对学生专业课水平的提升起到非常积极的促进作用。而且素质教育对学生数学应用以及实践能力提出了新的要求，即数学教学不仅要让学生理解和掌握其中的知识，还要能够学会应用和实践，解决生活中的问题[5]。但是受到有限的课堂时间、旧有教学理念、学生个体差异较大的影响，教师在实际教学中过分关注理论知识的讲解传授，忽略了对学生应用实践能力的培养，学生难以切身体会学习数学的乐趣和奥妙，无法认识到数学知识在生活中的应用价值，导致数学思维的培养受阻。数学知识的应用不足也是造成学生数学思维培养实效低下的重要因素之一。

三、培养高职学生数学思维的具体路径

（一）革新课堂教学观念，凸显学生主体地位

无论是义务教育阶段，还是高中、大学阶段，学生对知识的探究欲望以及积极性始终是培养学生学习能力以及学习思维的基础。只有提升和培养学生对知识的探究欲望，才能保障其在学习中获得更多的知识体验，深化其思维培养实效。因此，在实际教学中，教师应当注重革新以往的教学观念，引导学生进行自主探究，在探究中不断归纳、类比、创新，然后反向论证知识，这样才能够保障学生从中获得更多的知识体验[6]。教师要认识到只有学生积极参与实际教学，才能从中获得更多的学习体验，教学才能够更具实效。例如，在教学“数列的极限”一课时，教师在课堂伊始可以提出相应的探究问题，如“我国古代思想家庄周和数学家刘徽提出了什么数学理念？”“什么是极限思想？”等，在问题的引导下，学生会更加积极了解和掌握本章知识，而且数学文化故事的融入能够充分调动学生的学习积极性，对课堂教学质量的提升有着非常积极的促进作用。接下来，教师再引导学生逐渐了解“数列的极限”知识，由于本章知识有一定的难度，部分学生会因此产生抵触或者惧学心理，教师需要进行针对性引导，帮助学生从简单的概念入手，通过观察、归纳、总结规律来消除其不良学习心理。如教师可以引导学生研究函数值的变化趋势并分析无穷数列，从而发现数列的极限特征。在归纳总结的过程中，学生的数学思维能够得到培养和建设，对其综合的发展进步有着非常积极的作用[7]。

（二）发掘新型教学模式，增强学生应用能力

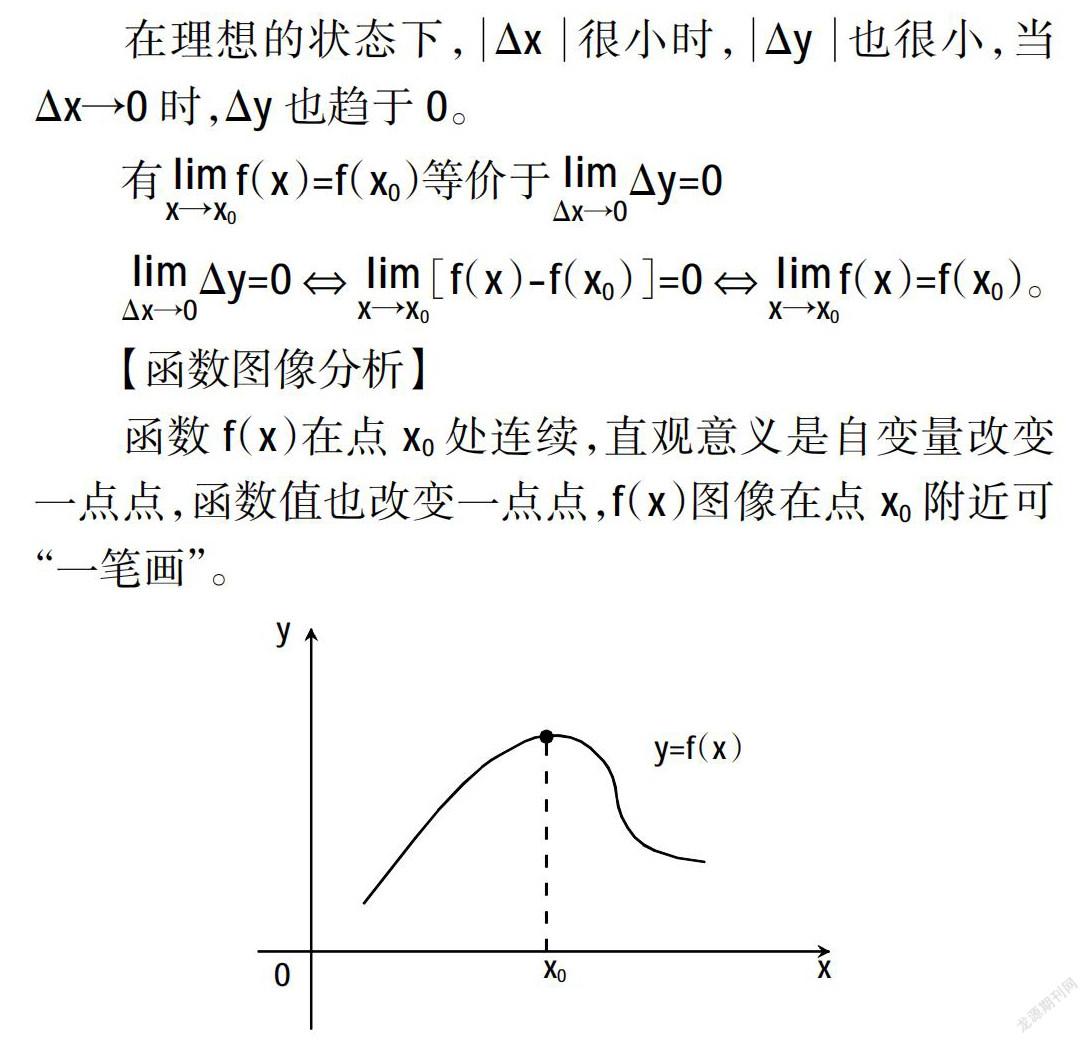
数学知识具有很强的实用性。因此，在实际教学中，教师应当注重教学模式的革新，改变以往过分关注理论教学的观念，结合学生的发展实际发掘生活中的数学知识，由此强化学生的数学应用能力。例如，在学习“函数的连续性与间断点”时，教师可以应用信息化教学设备，向学生展示相应的函数问题图像，然后为学生创设相应的学习探究环境，保障学生在积极融入情境的同时理解相应的知识，由此强化学生的数学应用能力。具体如下：

【问题】

在信息技术的演示下，学生能够快速地了解并掌握函数连续性与间断点的相关内容，教师趁热打铁，设置相应的课堂探究题引导学生再进行深入探究，以此强化学生的知识运用能力。在此过程中，学生的学习自主性能够得到充分培养和调动，并且教师还可以将相关的知识与学生的实际生活进行联系，引导学生从中更好地体会数学内容及其应用价值，这样整体教学更具实效[8]。

（三）创设问题探究情境，强化学生思维实效

教师可以在教学中创设问题探究情境，帮助学生在问题探究和感悟中获得更多不一样的学习体验，由此提升整体教学的有效性。在实际教学中，教师在设计相应的探究情境时可以选择符合学生认知水平并且具有启发性的问题，将学生的已知知识作为问题情境的切入点，既容易引导学生积极融入其中，并且还能借此强化学生的创新思维和逆向思维，对其数学综合素质的提升有非常积极的促进作用。例如学习洛必达法则时，教学前教师可以创设相应的问题探究情境，如复习和巩固函数的连续性求极限的相关知识，并以此作为本章课程探究学习的突破点，引导学生对相应的函数式进行分析解答，以此作为探究依据，指出其中求极限方法中的局限性，使學生在探究中能够明确洛必达法则学习的重要性。同时，教师在此过程中可以发掘学生认识中存在的矛盾冲突，并以此创设相应的学习情境，引导学生突破瓶颈，发挥逆向思维对相关问题不断进行分析和转化，提出新的问题然后再分析、解决，最终获得宝贵的学习体验[9]。

（四）注重分层教学，促进学生整体发展

在培养学生数学思维的过程中我们发现，受到学生年龄、兴趣、性格、习惯、态度、学习方法等的影响，学生在学习中会体现出一定的差异性，这种差异性在高职数学教学中表现得更加明显。因此，想要提升学生数学思维的培养实效，教师应当注重教学革新，深化分层教学，引导学生在原有基础上获得一定的发展，并从中获得相应的学习体验。还以“数列的极限”为例，在学生探究前，教师结合学生基础进行科学划分，基础较好的学生进行拓展学习，对知识进行深化应用;基础中等的学生则研究函数值的变化趋势，并分析无穷数列，并对其进行实践分析应用;基础较弱的学生则进行基础概念的掌握，对本章知识的应用进行简单理解和掌握。经过这样因材施教的教学实践，学生的数学思维培养将更具实效[10]。

四、结语

由此可见，受到高职数学教学多种因素的影响，学生的数学思维培养受到较大的限制，导致学生的数学学习水平得不到有效的建设和提升。针对这一现象，教师应当注重教学优化，结合高职数学教学中存在的困境加以针对性解决，突破以往教学模式以及观念，由此培养学生形成良好的数学思维。

参考文献：

[1]梁效科.浅谈高中数学教学中学生数学思维能力的培养[J].科技资讯，2020，18（6）.

[2]王立娜.高职数学教学中培养学生数学思维能力的途径研究[J].中国教育技术装备，2020（5）.

[3]徐慧.浅析高职学生数学思维、探索和实践能力的培养[J].发明与创新（职业教育），2020（10）.

[4]焦潍苹.基于微信平台高职生数学思维能力的培养策略研究[J].无线互联科技，2020，17（22）.

[5]许凌志.高职学生数学应用意识和能力培养的教学策略探讨[J].发明与创新（教育信息化），2020（1）.

[6]陈丽娜.高职数学教学中对学生创新思维能力的培养[J].数学学习与研究，2021（33）.

[7]杨蕊鑫.高职数学教学中学生应用数学能力与意识的培养方法[J].读好书，2021（21）.

[8]朱超武.高职数学教学中学生应用数学意识和能力的培养策略[J].山西青年，2020，589（17）.

[9]张国强，宋颢，王娅君.夯实基础，开拓视野，培养高职学生利用数学思想解决实际问题的能力[J].数学学习与研究，2020（3）.

[10]李琳.高职数学教学面临的问题与对策研究[J].湖北开放职业学院学报，2021，34（18）.

◎编辑 司 楠