基于速度场的露天矿卡车多路段行程时间组合预测模型
田凤亮, 王忠鑫,2, 孙效玉, 辛凤阳, 宋波, 王金金, 曾祥玉, 周浩, 赵明
(1. 中煤科工集团沈阳设计研究院有限公司,辽宁 沈阳 110015;2. 辽宁工程技术大学 矿业学院,辽宁 阜新 123000;3. 东北大学 资源与土木工程学院,辽宁 沈阳 110015)
0 引言
就露天矿电铲-卡车间断工艺生产效率而言,1个卡车作业周期内卡车行程时间的占比最高、变动幅度最大。准确的卡车行程时间预测是卡车优化调度的前提。受制于露天矿复杂多变的道路条件,实际生产中卡车优化调度系统在相当长一段时间内只实现了调度而非优化[1-3],其中一个重要原因是卡车在复合路段上的行程时间难以精准预测。
露天矿卡车行程时间受卡车性能、道路状况与环境因素的共同影响。一般来说,卡车行程时间可通过人工统计获取。但由于露天矿道路变动频繁,人工获取的时间往往很难用于生产组织工作[4]。当一条道路上的行程时间数据量足够支撑行程时间统计结果时,该道路可能已接近废弃。
在市政交通领域,国内外专家学者结合实际开展了行程时间预测研究[5],预测方法主要有历史趋势法、参数回归模型、时间序列、神经网络、支持向量机、卡尔曼滤波等[6-10]。露天矿卡车行程时间预测也可采用上述方法。从研究对象角度出发,可将露天矿卡车行程时间预测问题分为固定路段预测与动态预测两类[10]。固定路段行程时间预测的研究对象为固定起点与终点路段上的行程时间,而动态行程时间预测则研究道路上任意2点之间的行程时间。
固定路段行程时间预测的研究单元为单一路段。白润才[1]针对人工统计平均速度方法的局限性,提出了基于人工神经网络的露天矿卡车路段行程时间实时预测方法,较人工方法在预测精度和操作复杂度上都有明显改善。E. K. Chanda等[9]针对人工神经网络迭代次数多、收敛速度慢、容易陷入局部最小值而非全局最小值的问题,提出了基于自适应神经网络模糊系统的露天矿卡车行程时间预测方法,较人工神经网络在收敛速度和预测精度上有了进一步改善。Sun Xiaoyu等[10]提出了一种基于随机森林的卡车行程时间预测方法,将道路长度、卡车型号、驾驶人员等作为输入,获得了较高的预测精度。
与固定路段行程时间预测相比,动态行程时间预测更具实用性。孟小前[4]通过研究认为,进行露天矿卡车动态行程时间预测时,支持向量机的预测结果在一定程度上优于BP神经网络。K. Erarslan[11]研发了一套计算机辅助系统来预测卡车行程时间,可实时采集卡车速度,将距离除以速度来获得卡车行程时间预测结果。
上述文献研究的卡车行程时间预测方法或是在机理上进行细致刻画,或是从统计角度进行描述,预测结果往往具有很高的准确性。但露天矿道路复杂,导致上述理论方法在实际部署中存在困难。鉴此,本文提出一种基于速度场的露天矿卡车多路段行程时间组合预测模型,以历史数据构建卡车速度场,用于表征道路对卡车速度的影响,在此基础上分路段建立基于随机森林的行程时间单元预测模型,最终将单元预测模型预测结果累加,得出卡车在复合路段的行驶时间预测值。
1 多路段行程时间组合预测模型原理
露天矿卡车多路段行程时间组合预测模型由单元预测模型、累加器、速度场组成,其原理如图1所示。单元预测模型负责预测卡车在每一路段所需的具体时间。但该时间受卡车在路段上行驶的平均速度影响,而平均速度同样为未知数。这就要求在预测卡车行程时间之前,先估计卡车在该路段的平均速度。平均速度估计依赖卡车速度场,其可给出该路段任意一点上卡车可能的速度。以该速度为基础,单元预测模型可预测卡车经过该路段所需的时间。累加器负责将每个单元预测模型的预测结果相加,并作为最终预测结果输出。
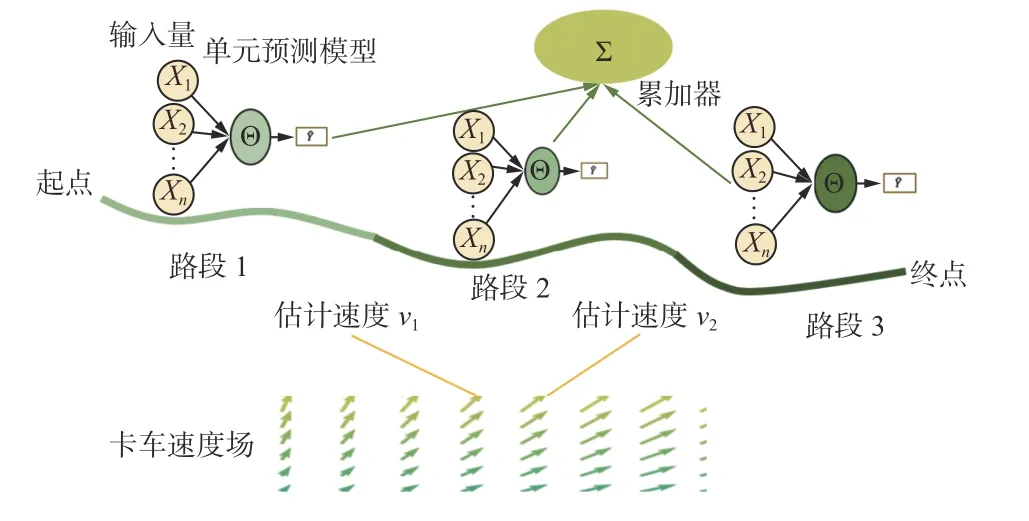
图1 露天矿卡车多路段行程时间组合预测模型原理Fig. 1 Principle of combined prediction model of multi section travel time of truck in open-pit mine
1.1 卡车速度场构建
场指物体在空间的分布情况,一般以空间位置函数表示。本文引入场的概念来表征卡车在整个矿区各条道路上的速度分布情况。卡车速度场反映了卡车速度与其在道路上具体位置的关系,卡车在道路上的位置不同,其速度也不同,如图2所示。其中x,y分别为矿区二维坐标,箭头指向为卡车行进方向,箭头长短表示卡车速度,箭头越长则速度越快。可看出当卡车行驶在右侧路段时,速度始终偏小;当卡车驶入左侧路段后,速度明显提升。这也验证了在预测卡车行程时间时,将整个行程作为研究对象是不合理的。

图2 露天矿卡车速度分布Fig. 2 Speed distribution of truck in open-pit mine
速度场可看作典型的二维场模型。二维场模型一般可通过不规则分布点法、规则分布点法、矩形区域法、不规则三角形法等表征[12]。速度数据在空间上均匀分布于各条道路,采用矩形区域法表征较合理。因此,选择矩形区域法表征卡车速度场。将整个矿山所在区域离散化为二维网格,将采集到的卡车速度信息映射到对应网格中。每个网格中的属性值为该网格中卡车速度平均值。当网格中无对应速度信息时,网格属性值为0。
露天矿卡车速度场如图3所示。颜色越亮,表示速度越大。可看出卡车在不同路段上的速度不同,在道路终点、两侧、交叉口处存在明显的减速现象。

图3 露天矿卡车速度场Fig. 3 Truck speed field in open-pit mine
1.2 单元预测模型选择
从统计角度看,卡车行程时间具有明显的规律性。但卡车行程时间是多因素耦合的结果[13-15],影响因素大致分为卡车属性、环境特征、道路因素3类。卡车属性主要包括卡车型号和载重状态。针对不同的生产需求,露天矿中卡车型号往往有多种。这些卡车的购入时间、保养状况、动力条件等不尽相同。卡车作业时分为空载和重载2种状态,重载状态下卡车行驶速度较慢。环境特征主要包括气象条件、昼夜变化等。露天矿卡车在不同季节的行程时间不同,昼夜行程时间也不同。道路因素主要指卡车行驶的路线信息,包括卡车行驶的起点、终点位置及其所经过路段的长度、提升高度等。道路因素是影响卡车行程时间最重要的因素。道路长度与提升高度会极大地影响卡车行程时间。当其他因素不变时,道路越长,提升高度越大,则卡车所需的行程时间越长。
卡车在路段上的平均速度影响卡车行程时间。定义卡车在某路段s上的速度为v(s),则理想状况下卡车行驶时间为

卡车速度不同时,其在该路段的行驶时间不同。
可见,影响卡车行程时间的主要因素有卡车型号、卡车载重状态、气象条件、卡车所经路段及其在该路段上的平均速度。这些因素有的是连续量,如道路长度、提升高度等;有的是离散量,如卡车型号、气象条件等。若采用支持向量机等算法,则需将离散信息量化,不可避免地存在一定程度的主观性。为了降低量化的主观性造成的精度损失,采用随机森林算法构建行程时间单元预测模型[16-18]。随机森林算法由多棵决策树组成。在构建决策树时,从训练数据集中有放回地随机选取部分样本,且随机选取部分特征进行训练。每棵决策树使用的样本和特征不同,训练结果也不同,可避免模型出现过拟合现象。
单元预测模型的输入包括卡车在所经过路段上的平均速度及文献[10]中的输入量,包括卡车ID、卡车类型、卡车状态、路段起点及终点位置、道路信息、气压、风速、温度、相对湿度、行驶时间等。
1.3 卡车平均速度计算
卡车在所经过路段上的平均速度是卡车行程时间预测的重要参数。将道路划分为多个单一路段后,单元预测模型并行计算每条路段上的卡车行驶时间。卡车在不同路段上的速度不同,而速度场只反映道路上各点卡车速度平均值,不是卡车在具体路段的平均速度,因此,对整条路段上所有点的卡车速度求平均值,将其近似为卡车在该路段的平均速度,即

式中:R为某路段上的所有网格区域;N为R中网格数;vr为网格r中卡车速度。
卡车不可能经过R中所有网格,因此只能近似表示卡车实际平均速度。本文中单元预测模型为随机森林算法,其为一种典型的统计学习算法,尽管并不严格等于平均速度,但在统计意义上依然是一种有效输入。以作为单元预测模型的输入,能更准确地预测卡车经过该路段所需的时间。
2 实验与结果分析
以2019年6-11月华能伊敏煤电有限责任公司伊敏露天矿卡车调度系统中220 t卡车1.8万条行程信息为基础数据,将其中1.5万条数据作为训练集,剩余0.3万条数据作为测试集,研究露天矿卡车多路段行程时间组合预测模型精度。采用随机森林拟合算法预测卡车行驶时间,以sklearn机器学习库中的RandomForestClassifier构建预测模型。采用分散训练、集中使用策略,先分别训练各路段上的单元预测模型,之后利用速度场将各单元预测模型整合。
模型输入变量中,离散量(如设备型号、日期、时间等)可直接输入模型,连续量中需要注意的是,道路信息既包括道路水平长度,也包含竖直方向的提升高度。本文通过计算道路中心线的方式获取道路信息。定义某路段上点的集合为P={x0,y0,z0,x1,y1,z1,···,xm,ym,zm},(xi,yi,zi)为 该 路 段 上 第i(i=1,2,…,m)个点的坐标,m为该路段上的点数。则该路段水平长度为

当卡车在该路段上处于上坡行驶时,提升高度为

式中zmax,zmin分别为运输过程中高程最大值与最小值。
当卡车处于下坡行驶时,提升高度为

对于大多数机器学习算法,需采用梯度下降方法求解最优解。为了保证模型有解,同时提高迭代速度,对输入的各连续变量进行归一化处理。
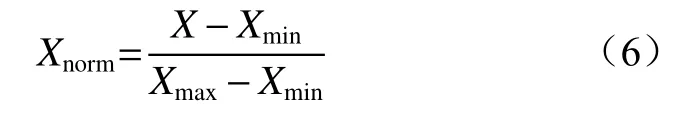
式中:Xnorm为输入量归一化值;X为输入量;Xmin,Xmax分别为输入量最小、最大值。
在模型训练过程中,采用穷举方法,通过在训练集中交叉验证方式寻找决策树数量最优值(本文为75)。该过程中参数设置:弱学习器数量为5~150,搜索步长为5,交叉验证可迭代次数为10。
采用测试集验证模型精度,预测结果与真实值之间的误差分布如图4所示。可看出预测误差主要集中在0~40 s,90%以上的预测误差小于1 min,1~2 min误差极少。通过分析误差来源,发现误差较大的行程时间其对应的路段数较多。

图4 组合预测模型的预测误差分布Fig. 4 Prediction error distribution of the combined prediction model
采用平均绝对误差百分比(Mean Absolute Percentage Error,MAPE)检验模型预测精度[19]。经计算,本文模型对卡车行程时间预测的MAPE为4.81%。
为了验证本文模型引入速度场及组合预测方法的优势,将其与文献[10]中的行程时间预测模型进行对比。基于相同的数据集,文献[10]模型的预测误差分布如图5所示。经计算,MAPE为7.02%。

图5 文献[10]中模型的预测误差分布Fig. 5 Prediction error distribution of the model in reference [10]
对比图4、图5可看出,本文模型所得结果较文献[10]方法准确,在相同的数据集下,MAPE降低2%以上。特别是针对地表维修站-坑下工作面之间几条较长的道路,本文模型的预测精度优势更明显:本文模型预测误差基本不超过120 s,而文献[10]中模型预测误差为100~215 s。
为了明确预测精度提高的原因,选取若干单一路段作为实验对象。经计算,在单一路段上,本文模型的MAPE为4.01%,文献[10]中模型的MAPE为4.33%,二者差别不大。文献[10]中预测模型也是基于随机森林算法构建的,与本文模型在特征选取及参数设置上无太大区别。不同之处是,本文模型考虑了每一条路段的特殊情况,是一种路段组合模型,且模型充分考虑了卡车在道路上行驶的平均速度。可见,将单一模型进行组合可有效提高预测精度。
本文模型输入量包括平均速度,因此在卡车处于任意位置、速度情况下,模型均能预测到达目的地的时间,即可实现卡车行驶时间动态预测。实时性是动态预测的重要指标。模型从接收数据到输出预测结果的平均运算时间如图6所示。可看出模型运算时间不超过1 s,可实时预测露天矿卡车行程时间。
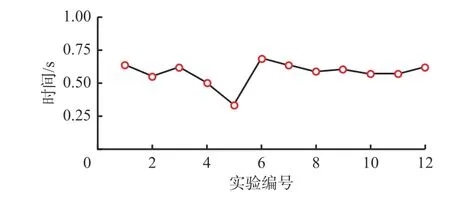
图6 组合预测模型运算时间Fig. 6 Operation time of the combined prediction model
3 结论
(1) 基于速度场的露天矿卡车多路段行程时间组合预测模型具有较高的预测精度,其MAPE较文献[10]中模型降低2%以上。
(2) 针对单一路段的行程时间预测,组合预测模型与单一模型相比无太大差别;针对复合路段行程时间预测,组合预测模型预测精度较单一模型高。露天矿实际生产中更多的是由不同行驶条件路段组成的复合道路,因此组合预测模型更适用于露天矿卡车行程时间预测。
(3) 露天矿卡车多路段行程时间组合预测模型中引入速度场,以卡车平均速度作为模型输入量之一,使得卡车行程时间动态预测成为可能。实验结果表明,该组合预测模型的运算时间不超过1 s,可实时预测卡车行程时间。

