面向5G广播的传输参数快速预测方法
胡 睿
(中央广播电视总台技术局,北京 100026)
1 研究背景
移动网络的高速发展,满足了人们对快速、大容量网络的需求,同时也带动了相关行业和产业的快速发展,5G的大规模商用将会给传统广电带来发展契机。5G网络低延时、高带宽的特点,使得超高清制作和转播成为可能。广电行业为适应市场发展,也开始逐步建设自身的云平台,为不同用户提供个性化服务,从而缓解网络新媒体带来的冲击[1]。广电相关业务还可以利用5G技术对原有传输速率进行优化来提升节目转播速率。与传统电视相比,5G通信网的诞生使电视机的功能得以创新,将电视与网络相结合,以网络电视的形式为用户提供丰富的服务功能[2]。综上所述,5G技术低时延、高可靠、低功耗、高速率、全覆盖等特性,正是广电媒体融合发展所需要的技术环境,它可以为媒体融合发展提供有力的技术支撑和技术保障,被广泛运用于广电媒体的各个部门和各项业务,使广电媒体发生根本性的变化[3]。
现阶段的视频、音频等广电媒体业务出现了飞速的发展,导致流量爆发式地增长,这会对5G通信网络造成巨大压力。而且无线电频谱资源作为无线通信的基本载体,其总量有限,若继续沿用原有技术,频谱资源匮乏问题将进一步加剧,难以满足未来不断扩大的通信容量和速率需求。毫米波大规模多输入多输出(MIMO)技术能解决5G无线通信系统面临的问题[4]。为深入挖掘大规模MIMO的性能增益,基站在进行预编码、波束设计时需要获取用户与每根基站天线之间大量的信道参数,包括到达角(DOA)、离开角(DOD)、时延和衰落系数,因此,精确的信道状态信息(CSI)是通信系统性能提升的关键[5]。在进行广播电视信号传输过程中,此时的信道可以称为广播信道。图1展示了针对该类信道的参数估计过程,接收端依据一定准则,从接收信号中将信道模型的模型参数估计出来。不同于传统的MIMO系统,大规模MIMO系统中天线数和用户数巨大,导致未知信道参量较多。因此,有效降低信道估计复杂度是实现大规模MIMO系统的重要前提。
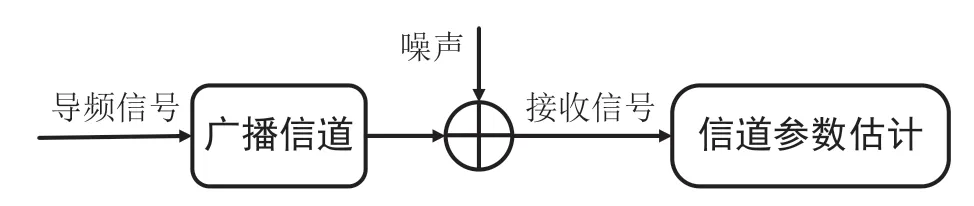
图1 广播信道估计原理框图
针对大规模MIMO系统,传统基于矩阵模型的信道估计方法,主要包括多重信号分类(MUSIC)方法和借助旋转不变性进行信号参数估计(ESPRIT)方法。由于将接收信号重构成矩阵形式损失了信号的多维信息,因此这类方法的估计性能较差,计算复杂度较高。本文针对现有广播信道估计方法进行分析,然后利用毫米波信道的稀疏散射特性和广播系统丰富的多维结构提出了一种快速信道估计方法。
2 基于5G的广电技术发展现状
2.1 5G与广播电视技术的融合
5G让移动通信网络技术速率得到了大幅的提升,它能传播更多的视频与音频资源,形成巨大的信息网络传播构架。在这样的技术背景下,通过科学合理的融合应用,能够助力广播电视行业的高速发展。多播技术与点到点或者点到面的广播技术的实践应用已经积累了较大的技术优势,而将5G技术与广播技术相互融合,成为移动通信行业技术发展的必然。在5G环境下,广电可以充分开展多样化的广播业务。当下广播电视领域采用点到点的广播方式,通过蜂窝移动通信网络进行移动视频内容的分发。在技术融合方面,5G技术对广播电视行业的发展提出了新要求,并进一步提出反向信道技术与应用信道技术,让广电更好地实现资源调拨[3]。
2.2 现有广播信道估计方法
文献[6]利用大规模MIMO信道的相关性,通过连续使用两次MUSIC方法来实现DOD和DOA的估计。为克服MUSIC方法依赖谱峰搜索导致计算复杂度过高问题,文献[7]提出了无须搜索的类ESPRIT方法实现DOA估计。针对频率选择性衰落信道,文献[8]利用该信道的稀疏性提出了基于多阶段压缩感知的信道估计方法。利用接收信号的低秩特性,周舟等人将毫米波大规模MIMO信道模型表示为多维信号模型,提出了基于多维矩阵分解的多参数联合估计方法[9]。针对具有双宽带效应的MIMO正交频分复用(OFDM)系统,文献[10]提出了基于结构化的多维矩阵分解方法来实现信道估计。为进一步节省频谱资源,文献[11]针对时变毫米波大规模MIMO信道,提出了一种基于优化的嵌套多维矩阵分解方法实现联合信道估计和符号检测。
3 所提信道估计方法实现
3.1 系统模型
利用毫米波信道的稀疏散射特性和大规模MIMO系统丰富的维度资源来构建多维接收信号模型。具体建模过程如下。
3.1.1 毫米波信道模型
考虑如图2所示的单小区毫米波大规模多用户MIMO广播系统,其中包含一个基站和多个用户。基站天线数和射频链路数分别为NBS和MBS,用户端天线数和射频链路数分别为NMS和MBS。对于第u(u=1,…,U)个用户,设基站和用户间的散射路径数为Lu,因此该用户的第lu(lu=1,…,Lu)条散射路径信息可以由时延lu、衰落系数和DOA这四个参数表征。考虑存在K个子载波,并随机选择其中K个子载波参与导频训练。

图2 单小区毫米波大规模MIMO广播系统
3.1.2 多维接收信号模型
对每个子载波而言,基站在 个有效的导频训练时间帧里发射 个不同的波束成形向量,当用户接收信号时,用户端首先将每个时间帧分成 个子帧,然后使用 个相互独立的合并向量来检测发射信号。当把 个子载波上的接收信号收集在一起后,即可将接收信号重构为三阶多维信号模型。
3.2 所提方法实现流程
所提方法运用前后平滑和酉变换技术,将上述复值多维信号模型转化为实值多维信号,以避免复值矩阵求解过程中过大的计算量,提高方法效率。该方法的实现流程如图3所示。

图3 所提方法实现流程
3.3 所提方法具体实现方法
在实现中,仅需依据图3对每个步骤进行扩充即可。
3.3.1 实值化多维信号模型
为简化复值多维信号模型的实值化过程,首先将预编码矩阵和合并矩阵设计为中心共轭对称矩阵;再将基站和用户端的导向矩阵中每列都转化为中心共轭对称向量。在完成上述两步预处理后,对复值多维信号模型的第3种模式展开执行实值化操作。
3.3.2 拟合实值信号模型
(1)随机初始化三个加载矩阵。
(2)每一步更新一个加载矩阵,对余下的加载矩阵依据前一次估计结果进行更新。
(3)重复步骤(2)直至收敛。
3.3.3 提取信道参数信息
根据多维矩阵模型分解唯一性,估计的实值加载矩阵存在共同的列模糊,即表明信道参数信息可以实现自动配对。此外,它们的尺度模糊也可以借助归一化消除。基于上述前提,利用简单相关方法从估计的加载矩阵中提取信道参数。
4 性能测试
我们利用MATLAB平台对所提方法和现有方法进行了仿真验证和比较,以证明所提方法在估计精度和计算复杂度上的性能优势。本实验考虑的单小区毫米波大规模MIMO广播系统参数配置如表1所示。

表1 系统仿真参数配置
我们比较了本文所提方法和现有方法的各个信道参数估计性能,并以均方误差(MSE)作为评价指标。图4给出了不同信道参数的MSE和CRB随SNR变化曲线,该图表明,所提方法和现有方法的参数估计曲线在中、高SNR场景下与CRB非常接近,只是衰落系数估计性能稍差。而且,所提方法的信道参数MSE曲线都位于现有方法对应曲线下方,尤其在低SNR情况下,意味着所提方法的信道参数估计精度优于现有方法。
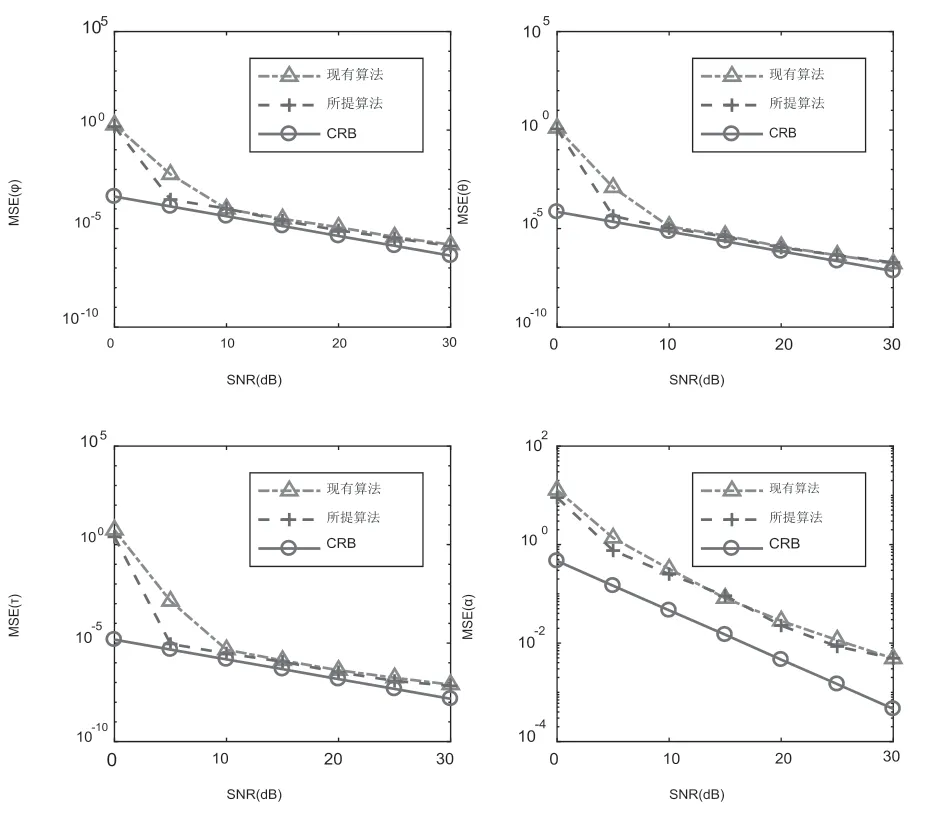
图4 不同信道参数估计性能与SNR关系
我们还比较了所提方法和现有方法的复合信道估计性能,并以归一化均方误差(NMSE)作为评价指标。图5给出了在不同时间帧 下,复合信道矩阵的NMSE随SNR变化曲线。该图表明,所提方法能够提供比现有方法更高的估计精度,特别在较少时间帧T场景中。而且随着时间帧T的增加,两种方法的复合信道估计性能都相应提高。

图5 不同时间帧 下的复合信道估计性能与SNR关系
最后,我们比较了所提方法和现有方法的平均迭代次数,以反映总体计算复杂度。表2给出了两种方法的平均迭代次数随SNR变化情况。结果表明,随着SNR的增加,所提方法的平均迭代次数始终小于现有方法。尽管实值多维信号模型的样本量增加了一倍,但由于实值矩阵求解过程会大大降低计算负担,因此所提方法的计算复杂度仍低于现有方法。

表2 海上应急通信示范验证测试记录表

表2 所提方法和现有方法的平均迭代次数比较
5 结束语
对于单小区毫米波大规模MIMO广播系统中的多信道参数联合估计问题,现有信道估计方法都具有较高复杂度。为此,本文利用毫米波信道的稀疏散射特性和大规模MIMO广播系统丰富的多维资源,提出了一种快速信道估计方法拟合实值多维信号模型。测试结果表明,本文所提方法在保证估计精度不变甚至略高于现有方法的情况下,可以进一步降低计算复杂度,优化系统性能。■

