基于BB-VIKOR法的新型智慧城市建设质量评价研究

王铁旦，李诗瑶，彭定洪

(昆明理工大学 a.管理与经济学院；b.质量发展研究院，云南 昆明 650500)

一、文献综述与方法运用

(一)文献综述

国际商业机器公司(International Business Machines Corporation，IBM)于2008年提出智慧城市[1]的概念后，引起了美国、新加坡、日本等众多国家的积极响应[2-4]。我国在2013年首次进行智慧城市试点活动并于2016年提出新型智慧城市的概念，不同于国外的智慧城市理念重在对“物”的管理，我国的新型智慧城市建设核心是以“人”为本[5]。因此，如何从“人本”角度对新型智慧城市建设质量进行评价成为当前亟待解决的问题。截止2021年，中国有超过700个城市开展智慧城市建设，数量上是全球第一，然而“量”的增加并不等于“质”的提升。科学合理的评价可以有效地反映出智慧城市建设质量与运行效果，本文通过对前期建设经验进行总结和梳理，尝试为后续管理和发展提供有益借鉴。

新型智慧城市建设质量的精准评价需要科学合理的方法和模型。目前，我国对智慧城市评价的相关研究主要有两类：一是基于客观数据的分析。刘笑音等[6]、胡军燕等[7]分别采用主成分和面板数据对智慧城市发展潜力和智慧度进行分析；随后，客观数据结合各类模型相继被运用到智慧城市评价领域。陈莉等[8]采用熵权与云模型相结合的方法来评价我国的绿色智慧城市发展水平。邹凯等[9]构建了灰色关联分析-反向传播神经网络(Grey Relational Analysis-Back Propagation Neural Network，GRA-BPNN)智慧城市发展潜力评价模型。随着城市发展趋势由“物本”转向“人本”，其关注的焦点从最初的“物”的发展落到“人”的感受上[10]，即智慧城市建设是以提升人民群众的幸福感和满意度为核心，因此，仅依据统计数据来衡量具有局限性。二是基于专家打分的主观数据分析。项勇等[11]提出构建智慧城市评价体系的网络关系图，再用逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)衡量城市的智慧程度。何琴[12]以层次分析法( Analytic Hierarchy Process，AHP)为基础构建了智慧城市建设水平评价模型。王枫等[13]利用概率语言评价从市民获得感角度出发，对新型智慧城市建设的三个方面进行了评价。

城市发展质量测评经历了由单一指标测评向复杂指标体系发展且在评价过程中越来越突出主观评价的作用[14]。智慧城市建设方面的专家，作为“人”感受的评价者具有较高的权威性和代表性。由于个体差异性，专家在评价过程中难以达成共识，而基于聚合算子的信息聚合技术如等权的处理方法进行数学平均或少数服从多数等容易导致具有建设性的少数意见被忽视[15]。Peng J J等人也指出在评价决策领域处理评价信息时简单的删除重复值是不合理的，忽视重复值也可能造成部分决策者偏好信息的丢失[16-17]。本文选取Yager R R[18]提出的模糊包(Fuzzy bags)对专家意见进行整体表征，不仅可以解决专家意见不一致难以达成共识的问题，也可以有效对原始重复信息进行保留。

(二)方法运用

新型智慧城市建设质量评价包含了多方面内容，如城市经济、生活、环境等，其评价过程属于典型的多属性评价问题。对新型智慧城市建设质量进行评价的目的是了解城市在建设中所处的阶段和水平，而非择优，且城市在各方面建设过程中的表现参差不齐，所以选择妥协评价方法更贴合实际情况。多准则妥协解排序法(VlseKriterijumska Optimizacija IKompromisno Resenje，VIKOR)不仅能解决智慧城市评价指标间的冲突问题，还可以通过最大化群体效用和最小化个体遗憾对有限决策方案进行折衷排序，寻求总体满意度和个体满意度之间的平衡，有效解决决策群体由于决策背景、决策偏好等差异造成的评价结果与集体利益相悖的问题[19]；同时，VIKOR法中虽提及负理想解，但它仅用于规范化距离分量而未作为评价参考，与实际运用中对建设质量最差的城市关注度远不及发展质量最好的城市相符[20]。

综上，本文综合现有研究成果提出了一套符合我国新型智慧城市建设质量评价的指标体系，并同步构建了基于模糊包的VIKOR方法(BB-VIKOR方法)用于我国新型智慧城市建设质量评价。在评价过程中采用模糊包的形式对专家评价信息进行整体表征，并通过构造模糊包线性偏好函数解决了两个长短不一致的模糊包的大小比较问题，而改进的多属性模糊包间的距离公式则能更好地将VIKOR方法运用在模糊包领域。

二、新型智慧城市建设质量评价指标构建

IBM作为智慧城市概念的提出者，从城市服务、市民、商业、交通、通信、供水、能源7个方面制定了一套用于评价智慧城市建设质量的指标体系。此外，在国际上认可度较高的还有智慧社区论坛(Intelligent Community Forum, ICF)每年进行的“年度智慧社区”评选。该评选1999年开始从宽带连接、知识劳动力、创新型、消除数字鸿沟、市场营销和宣传及2015年新加入的可持续性这几项永久评选主题指标进行评选。由于发展时间较长，它的评选标准及流程相对来说都比较完善。欧盟智慧城市研究自2007年开始以来，主要从智慧经济、智慧移动、智慧环境、智慧公民、智慧生活、智慧治理6个方面分别对欧洲中等规模城市进行评价分析[21-22]。国内方面，我国2011年7月发布的《智慧城市指标体系1.0》是首个评价智慧城市建设质量的指标体系，主要从智慧城市基础设施、智慧城市公共管理服务、智慧城市信息服务经济发展、智慧城市人文科学素养、智慧城市市民主观感知5个维度进行衡量。2016年，国家提出了新型智慧城市的概念，并设立了《新型智慧城市评价指标体系3.0》，主要从惠民服务、精准治理、生态宜居、智能设施、信息资源、网络安全、改革创新和市民体验8个方面进行考核。发改委、网信办2018年联合发布的《新型智慧城市评价指标》则包含了惠民服务、精准治理、生态宜居、智能设施、信息资源、创新发展、市民体验7个方面[23]33-38。

有学者对比了几套评价指标体系，指出欧盟的指标体系相对来说最为完善[25-26],但欧盟和我国新型智慧城市发展的侧重点不一致，且该套指标体系确立较早，已不能包含现代城市发展的一些其它要求。新型智慧城市和传统智慧城市最大的区别就是“人本主义”的突出体现，目的是使城市居民获得更高的幸福感。从2017年以来的研究成果(见表1)可看出关于民生的衡量指标越来越多，尽管指标名称不完全一致，但其内涵都是对民生、市民感受等方面的评价。另外，随着互联网技术的高速发展，过去只单纯考虑网络覆盖情况已不足以衡量城市的网络智慧质量。“互联网+”成为城市发展的主流，互联网技术的应用水平更能体现其智慧程度，如移动互联网、云计算、大数据、物联网等与现代制造业、政务服务、社会治理等方面的结合。基于此，本文以欧盟指标体系为基础并结合国内相关研究，在充分考虑新型智慧城市的建设目标和特点后提出如表2所示的指标体系，即从智慧经济、智慧环境、智慧设施、智慧公民、智慧生活、智慧治理、智慧互联、智慧民生8个方面较为全面、系统地评价了新型智慧城市建设质量。

表1 智慧城市评价指标研究

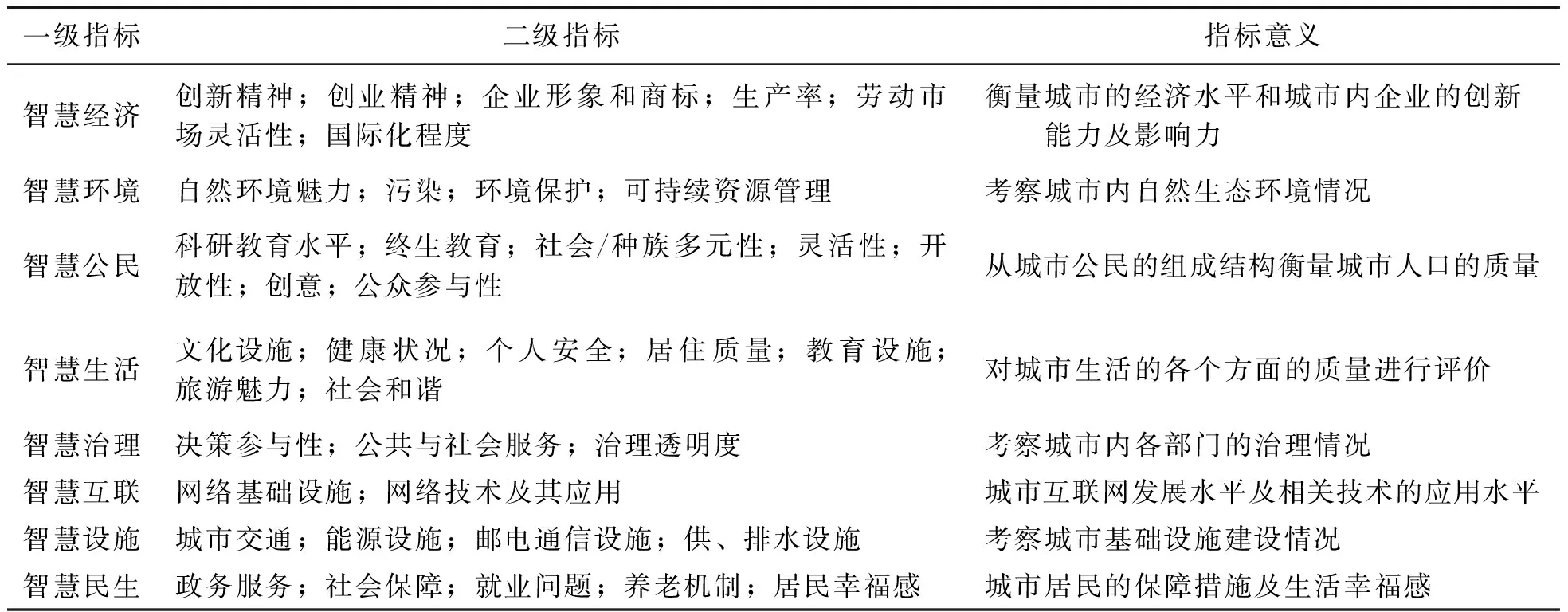
表2 新型智慧城市评价指标体系

三、 新型智慧城市建设质量评价方法的构建

新型智慧城市建设是一个长期且复杂的过程，其质量评价涉及城市经济、环境、治理等方面的建设情况，属于多属性评价的范畴。在评价过程中，不同的指标间、专家的评价结果中都可能出现冲突，VIKOR方法作为典型的妥协评价方法用于城市建设质量评价中可以较好地解决该问题。专家作为“人”的代表，在新型智慧城市建设质量评价时往往难以给出精准的评价值，该过程充满了模糊性和不确定性。为降低主观偏见对评价结果的影响往往邀请多个专家对智慧城市建设质量进行评价。由于多准则决策中，共识过程繁琐且难以达成，有效地考虑多专家的意见来表征群体意见至关重要。模糊包较之其它模糊集形式，不仅兼容了不可调和的观点，其计数值也简洁有效地对群决策中重复意见进行了保留。假设两位专家对某一智慧城市经济方面进行评价，一位专家在0.5和0.6之间犹豫，另一位专家给出0.6的评价，则该方面的评价结果用模糊包A表示为A=[CountA(u/x)/(u/x)]=[1/0.5,2/0.6]。其中，u表示专家给出的隶属度打分值，u∈[0,1]，CountA(u/x)表示打分值u出现的次数。

(一) 模糊包偏好函数及距离测度

将专家群体的评价信息用模糊包的形式表征后，采用VIKOR方法对新型智慧城市建设质量进行排序。表征专家群体评价信息的模糊包的大小比较是选择正、负理想解的关键，如何有效确定多个模糊包的优劣是该方法应用的关键。偏好关系，作为一种有效的决策信息表达方式，可以通过决策者针对评估对象进行两两比较得到相应的决策信息[35]。假设有m个方案(j=1,2,…,m)，n个属性(i=1,2,…,n)，Ci(x)，Ci(y)分别为方案的评价值，则优等分数[36]143-162：

Si(x)=Card({y∈X/Ci(x)>Ci(y)}) (1)

式中：Ci(x)>Ci(y)表示在属性i中方案x“击败”方案y。

当对两个长短不一的模糊包进行比较时，需要将其添零补齐或采取对元素按降序排列后补齐[37]。但是，该类方法存在一定缺陷，根据决策者的主观偏好添加的数值不同排序结果也会不同。本文基于穷举的思想，对模糊包内元素进行逐一比较，根据线性准则提出了如式(2)所示的模糊包线性偏好函数，用于比较两个模糊包M、N的优劣大小关系。M的长度为lM，N的长度为lN，则优势偏差函数为：

(2)

式中：i={1,2,…,lM}，j={1,2,…,lN}，Sn={1,2,…,lM·lN}，umax=max{u1,u2,…,ui+j}，umin= min{u1,u2,…,ui+j}。

计数值Count表示每个犹豫偏差可能出现的次数，由于在比较时穷举了每一种可能，在专家权重一致的情况下，其作用等同于概率作用。用一个偏差值的计数除以该部分偏差的总计数值，就是此偏差值可能出现的概率。因此，通过偏差值和计数值的整合可以得到如式(3)所示的优势偏好函数。

(3)

在确定正、负理想解后，需要计算出各城市评价值与理想解的距离，从而确定城市建设质量的优劣情况。为充分利用决策信息，本文构造各方案的多属性模糊包，主要由三部分组成：初始评价模糊包(Bi)，指标权重(Πi)和属性(Ci)，避免了后续将权重与决策信息融合的问题。

MCFBj=[Bi/Πi/Ci]

=[(Count(ui)/ui)/Πi/Ci](i=1,2…n)

(4)

由于添加了指标权重，其形式与规范模糊包形式存在差异，模糊包距离公式也不再适用。因此，本文对原有距离公式进行改进，提出了新的距离公式，如式(5)所示。设MCFB1,MCFB2为任意两个多属性模糊包，则其距离计算公式为：

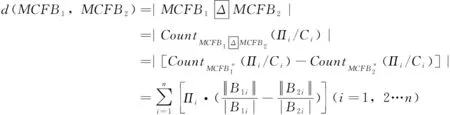
(5)

(二) BB-VIKOR方法的具体步骤

步骤1:获得初始决策矩阵。多名专家对不同的新型智慧城市建设质量进行评价(本文假设专家权重相等)，得到模糊包矩阵D=(Bij)m×n。该模糊包矩阵含两部分内容，即除了专家评价的隶属度值(uij)，还有每个隶属度值出现的次数Count(uij)，而原始信息得以充分保留。

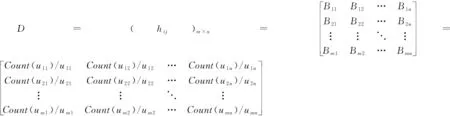
(6)

步骤2:确定不同城市在同一指标下建设质量的优劣程度。根据式(2)可以得到同一指标中城市Ai与其它城市相比建设质量的优势偏差程度，式(3)则可以计算出城市的最终优势偏好值。S越接近1，表示城市Ai在该方面的建设质量优于其它城市的程度越高。

步骤3:根据同一指标下的城市建设最终优势偏好值选出正、负理想点A+,A-。

A+={S1+,S2+,…,Sn+}={max(S11,S21,…,Sm1),max(S12,S22,…,Sm2),…,max(S1n,S2n,…,Smn)}

(7)

A-={S1-,S2-,…,Sn-}={min(S11,S21,…,Sm1),min(S12,S22,…,Sm2),…,min(S1n,S2n,…,Smn)}

(8)

步骤4:根据式(4)构造多属性模糊包。多属性模糊包在本处作用是对同一城市的信息进行集结，包含多个指标下的模糊包信息。由步骤3选择的正、负理想解所对应的模糊包可以确定正、负多属性模糊包。

(9)

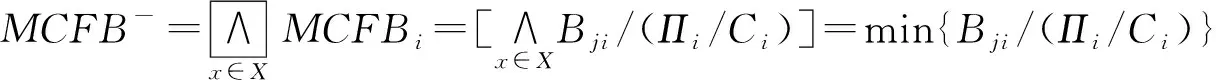
(10)

步骤5:计算各多属性模糊包与正、负理想多属性模糊包的距离，能有效衡量各城市实际表现与理想点之间的偏离程度。

(11)

(12)

步骤6:根据利益比率值Qi的大小进行排序，判断新型智慧城市建设的质量情况。Qi值越小，表示城市建设质量越好。

Sj=[d(MCFBj,MCFB+)/d(MCFB+,MCFB-)]

(13)

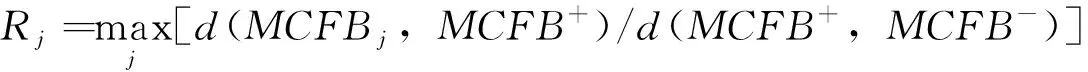
(14)

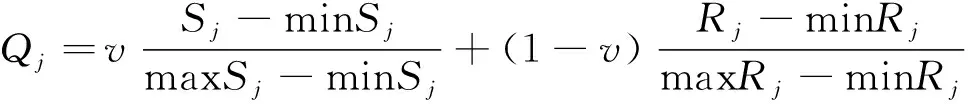
(15)

式中：v表示决策系数，且v∈[0,1]，取值根据决策者的偏好而定。为方便计算，本文取v=0.5。

四、实例验证

随着我国开放程度的进一步加大，边境城市的重要性日益凸显，云南省作为我国与东南亚连接的“窗口”，其城市智慧化建设发展具有重大意义。为对云南省新型智慧城市建设质量进行评价，本文选取东部城市曲靖、省会城市昆明、中部城市玉溪、南部城市红河州及普洱、西部城市大理以及北部城市昭通市在内的7个城市(A=A1,A2,…,A7)为例，由3位专家(因各个专家知识背景不同，在评价中均具有其自身的优势，本文视各个专家为同等重要)从智慧经济、智慧环境、智慧设施、智慧公民、智慧生活、智慧治理、智慧民生、智慧互联(C=C1,C2,…,C8)8个方面来进行智慧城市建设质量评价。指标权重值Π=(Π1,Π2,…,Π8)=(0.2,0.1,0.1,0.1,0.1,0.1,0.2,0.1)(权重通过AHP层次分析法获得)。每位专家尽可能独立地对城市建设质量进行评价，评分值在[0,1]范围内，分数越高表示对智慧城市建设质量越满意。

第一步，将所有专家的评价信息进行集结，得到如下所示初始模糊包矩阵R=(rji)7×8，实现了对原始信息的充分保留。

第二步，在已知各属性下的专家评价之后，获得各属性下不同方案的偏差程度以计算偏好值。以指标C1为例(下同)，得到表3所示的模糊包偏差表。

表3 C1指标下的模糊包偏差表

随后，利用公式(3)对偏差矩阵进行处理，得到表4所示的模糊包偏好函数值。

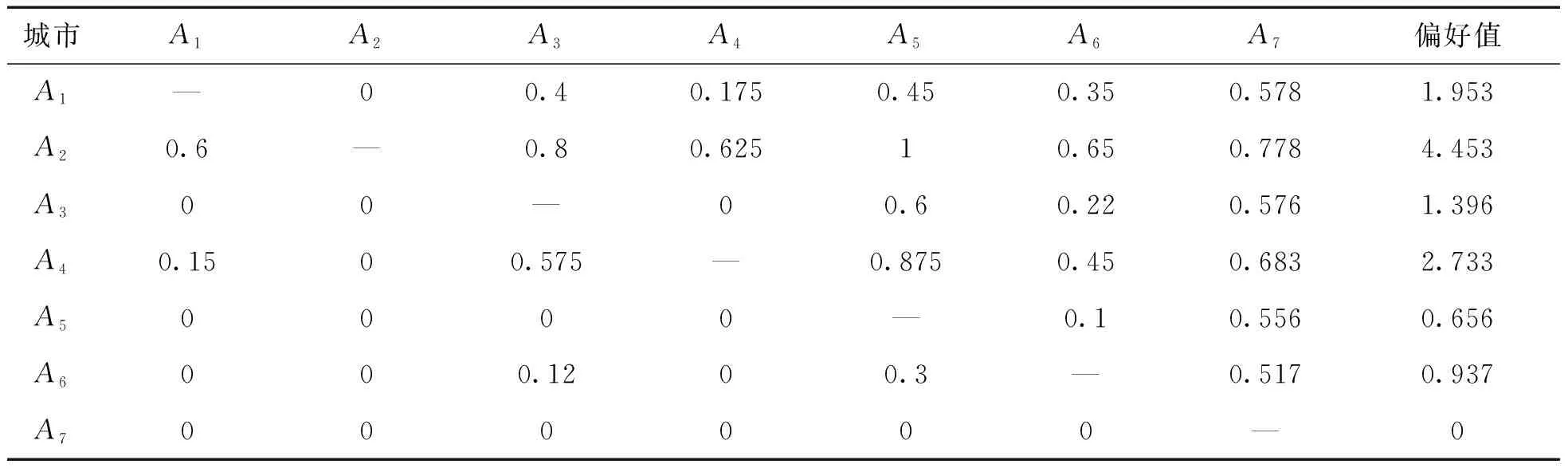
表4 C1指标下的各方案的偏好值

第三步，偏好值反映了同一指标下方案的优越性程度，对方案的优劣比较具有重要作用，根据偏好值的大小选取正、负理想点，如下所示：

S1+=max(S11,S21,…,Sm1)=max(1.953,4.453,1.396,2.733,0.656,0.972,0)=4.453

S1-=min(S11,S21,…,Sm1)=min(1.953,4.453,1.396,2.733,0.656,0.972,0)=0

第四步，构造各方案的多属性模糊包，对现有信息进行融合，不需要再考虑如何选择算子将权重整合的问题。以城市A1(曲靖)为例，构造多属性模糊包MCFB1，其余算法相同；同时，由于上一步确定了正、负理想点，据此可以确定出正、负多属性模糊包(MCFBs)：

第五步，计算多属性模糊包与正、负理想多属性模糊包间的距离。以城市A1(曲靖)为例，其余算法相同。

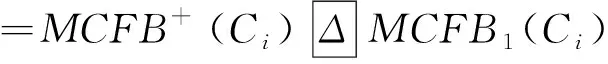
=[0.12/0.2/C1;0.042/0.1/C2;0/0.1/C3;0/0.1/C4;

0.025/0.1/C5;0/0.1/C6;0/0.2/C7;0/0.1/C8]

=0.12×0.2+0.042×0.1+0×0.1+0×0.1+0.025×0.1+0×0.1+0×0.2+0×0.1=0.031

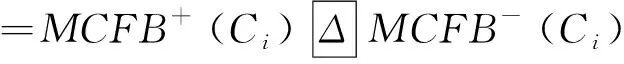
=0.467×0.2+0.355×0.1+0.267×0.1+0.308×0.1+0.367×0.1+0.375×0.1+0.475×0.2+0.533×0.1

=0.409

第六步，计算最大群体效益值Si和最小个体遗憾值Ri，由此可得到利益比率值Qi，并根据计算结果对新型智慧城市建设质量进行排序，最终计算结果如表5所示。

表5 Si,Ri,Qi结果

S1=d(MCFB1(Cj),MCFB+(Cj))/d(MCFB+(Cj),MCFB-(Cj))

=0.031×c0.409=0.076

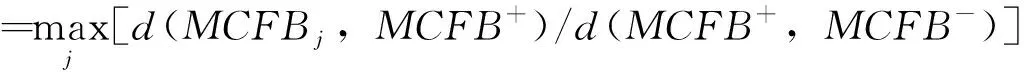
=max(0.257,0.118,0,0,0.068,0,0,0)

=0.257

通过分析可得出新型智慧城市建设质量排名为A2>A1>A3>A6>A4>A5>A7，即由高到低依次是昆明、曲靖、玉溪、大理、红河州、普洱、昭通。

为验证该方法的有效性，将其结果与采用Rebai A提出的BB-TOPSIS方法[36]143-162的结果进行比较，结果如表6所示。

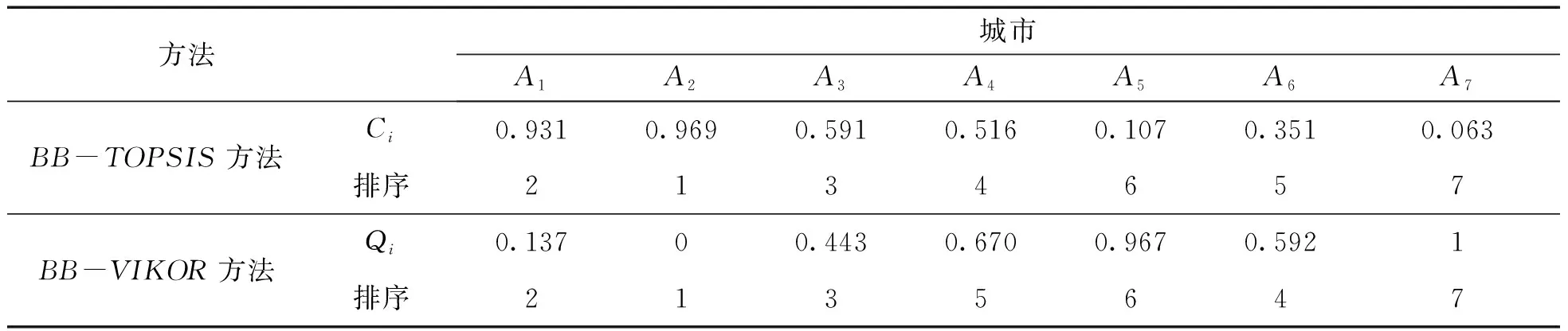
表6 两种不同方法评价结果

两种方法所得的智慧城市建设质量排名一致性较高，差别在于第4名和第5名排序不同。造成这种差异的主要原因是采用BB-VIKOR方法中排名第5的红河州在智慧环境和智慧互联方面表现较差，从而导致个体遗憾值偏大，最终排名靠后。实际情况中，高质量智慧城市需要城市在各方面都表现优秀，任意一方面出现短板都会影响城市的建设和发展，所以红河州排名应在大理之后，与本文方法所得结论一致。

从评价结果看，昆明作为云南省的省会城市，在城市建设各方面都表现较好。曲靖市在许多方面得分值较高，但由于经济和环境相对昆明来说差距较大，导致曲靖最终利益比率值高于昆明。普洱市在智慧环境和智慧民生方面的建设存在不足，导致其个体遗憾值Ri较大，影响了排名。昭通作为云南省北部发展较快的城市，虽然在智慧环境等方面有优势，但在智慧经济、智慧互联等方面还有较大的提升空间。总体来看，云南省新型智慧城市建设仍然呈现出地域差异，省会城市及靠近省会的城市集群建设成效更好；同时，距离昆明较远的大理及红河州的快速发展也为其它城市的建设提供了参考。综上，各城市应该结合自身特点，吸收借鉴其它城市建设经验以实现城市高质量发展。

五、结论

本文从“人本”角度出发，基于主观数据对我国新型智慧城市建设质量进行评价。首先，对国内外政府部门发布的文件和近几年相关学者的研究进行梳理，以欧盟指标体系为基础，结合研究热点构建了智慧经济、智慧环境、智慧设施、智慧公民、智慧生活、智慧治理、智慧民生、智慧互联8个维度的评价指标体系。随后，提出BB-VIKOR方法用以评价新型智慧城市建设质量。采取模糊包的形式对专家意见进行整体表征，不仅考虑了决策过程中的重复信息，也对少数群体性意见进行了保留，使决策更加科学合理。另外，通过构造模糊包线性偏好函数解决了长短不一致的两个模糊包的大小比较问题，避免了添值和排序的影响，更有效地反映出其优势程度；同时，改进的多属性模糊包的距离公式有效衡量了各城市实际表现与理想点之间的偏离程度，解决了BB-VIKOR方法在应用中的距离计算问题。最后，以我国云南省部分城市为例，验证了方法的可用性，所得结论与实际情况相符。