电驱动机械臂的自抗扰鲁棒哈密顿跟踪控制

曾庆山，周亚帅，陶长春，刘艳红

(郑州大学 电气工程学院，河南 郑州 450001)

0 引言

高精度的关节位置跟踪是机器人领域的基本需求。为了降低位置跟踪控制器的设计难度，执行器的动态模型往往被忽略。然而忽略掉执行器的动态，闭环系统的性能可能会降低，甚至不稳定[1]。永磁同步电机(permanent magnet synchronous motors，PMSM)具有转矩体积比大、精度高、调速范围宽等优点[2-4]，是机器人系统的常用执行装置。

电驱动机械臂的跟踪控制包括位置跟踪[5-6]以及电流跟踪[7]。徐旭等[8]设计了位置协调控制器和反步法电流控制器，但没有考虑系统不确定性的影响。Xue等[9]设计了改进的模糊反步法位置控制器，但是没有考虑电机动态的参数变化及其扰动。Khorashadizadeh等[10]设计了自适应模糊控制器对总的不确定性进行估计和补偿。Keighobadi等[11]和Saleki等[12]针对永磁直流电机驱动机械臂系统的轨迹跟踪，利用机械臂是电机的负载这个事实，把机械臂动态转换到电气动态，分别设计了自适应鲁棒反步法控制器和无模型自抗扰控制器(active disturbance rejection control，ADRC)。

Ortega等[13]提出的互联和阻尼配置(interconnections and damping assignment，IDA)由于具有物理意义明确、易于设计的优点，被广泛用于哈密顿系统控制设计，此外利用了哈密顿系统的结构和能量特性，便于进行闭环系统稳定性分析和H∞控制器设计[3]。但是该方法依赖于系统模型，所设计的鲁棒控制器具有一定的保守性。Han[14]提出的ADRC对模型的依赖程度低，可同时提高系统的抗扰性能和跟踪控制精度，得以广泛应用。Han等[7]和金宁治等[15]将ADRC与IDA相结合，取得了很好的控制效果。但由于控制增益的不确定性也归入到总扰动中会导致总扰动的估计出现误差，从而使ADRC控制性能降低[16]，对此一些学者在ADRC中引入滑模控制[17]和改进扩张状态观测器结构[18](extended state observer，ESO)处理剩余的扰动观测误差。

1 机器人系统动态模型

考虑n个PMSM驱动n个关节的机器人系统，假定机械系统是刚性的，每一个连杆由一个PMSM通过齿轮驱动。带有不确定性的第i个关节和电机的机械方程可描述为[11,13,19]

(1)

(2)

式中：Qi、θi分别为第i个关节和电机转子的位置，rad；Mij、Cij、Gi、Fi、τLi、τMi、τexti分别为惯性矩阵元素、哥式力和离心力矩阵元素、重力矩矩阵元素、关节摩擦力矩矩阵元素、负载转矩矩阵元素、电磁转矩矩阵元素、外部扰动向量的元素；Ji、Bi分别为电机的惯性矩阵的元素和阻尼矩阵的元素；ki为齿轮减速比系数。

假定传动装置是刚性的，没有间隙，转子位置θi和关节位置Qi存在线性关系Qi=kiθi，将式(2)代入到式(1)得

(3)

(4)

第i个PMSM的电磁转矩和电气动态为[2-4,7]

(6)

式(6)的状态向量、输入向量、输出向量和扰动向量定义为

(7)

式(6)的哈密顿函数选择为

(8)

则式(6)的端口受控耗散哈密顿结构为

(9)

式中：J(xi)为互联矩阵；R为阻尼矩阵；g、g1分别为控制输入和扰动输入矩阵，分别为

2 控制系统设计

2.1 级联ESO位置控制器设计

(10)

fmi+τdisi)。

(11)

式(10)状态向量和输入向量定义为

(12)

式(10)的扩张状态空间模型为

(13)

第1个ESO设计为

(14)

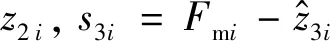
(15)

式中：α1i、α2i、α3i为观测器增益。

根据极点配置，两个ESO的观测器增益可选择为

(16)

(17)

2.2 鲁棒IDA控制器设计

当不考虑扰动时，期望的哈密顿函数选择为

(18)

(19)

式中：

期望的状态误差闭环哈密顿结构设计为

(20)

令式(19)和式(20)相等，计算可得u1i为

(21)

考虑扰动，式(21)代入到式(9)可得

(22)

式(22)的H∞控制问题[3]可描述为：设计u2i，使得哈密顿-雅克比不等式恒成立，即

(23)

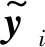
(24)

(25)

因此鲁棒IDA控制器为

(26)

2.3 改进的鲁棒IDA控制器设计

(27)

式中：εi>0为变增益所选择的设定值。

3 稳定性分析

位置跟踪误差定义为esi=Qi-Qides，将式(17)代入到式(10)，整理可得

(28)

(29)

(30)

4 仿真验证

图1 电驱动机械臂系统的控制结构图Figure 1 Control structure diagram of electrically driven manipulator system

图2 级联ESO与传统ESO的位置跟踪误差对比Figure 2 Position tracking error comparison between cascaded ESO and traditional ESO

其次，对改进的鲁棒IDA控制与IDA控制进行比较，关节位置跟踪和电流跟踪对比如图3和图4所示。可以看出，即使采用了级联ESO，IDA控制的位置跟踪精度仍相对较低，说明即使机械子系统有很强的鲁棒性，电气子系统的不确定性仍能影响到位置跟踪性能；而改进的鲁棒IDA控制有效抑制了电气子系统的不确定性，从而保证了位置、电流的高稳态跟踪精度。改进的鲁棒控制器与哈密顿控制器相比，关节位置跟踪精度提升了0.005 rad，电流跟踪精度也显著提升。

图3 改进的鲁棒IDA与IDA的位置跟踪误差对比Figure 3 Position tracking error comparison between improved robust IDA and IDA

图4 改进的鲁棒IDA与IDA的电流跟踪误差对比Figure 4 Current tracking error comparison between improved robust IDA and IDA

再次，将改进的鲁棒IDA控制与鲁棒IDA控制进行控制电压对比，如图5所示。可以看出,直接在IDA上引入H∞，初始控制电压特别大；若改进H∞引入的时机，可以极大地改善初始控制电压大的问题。

图5 改进的鲁棒IDA与鲁棒IDA的电压对比Figure 5 Voltage comparison between improved robust IDA and robust IDA

5 结论