黄河流域重要断面设计年径流量计算研究

杜 懿，孟 越，陈昱桢，王大刚

（中山大学 地理科学与规划学院，广东 广州 510275）

水文频率分析的目的是为水利工程的规划、设计和建设等提供科学依据，其首要工作就是对研究序列进行“三性”（可靠性、代表性和一致性）审查。 在过去相当长一段时间内，人类活动的范围和强度有限，对自然环境的影响不大，一般经整编后的水文资料序列均能满足一致性要求。 但是，近年来，随着全球气候变化以及人类活动对自然界的大规模改造，水文时间序列的一致性要求不再得到普遍的满足［1］。 为此，水文工作者进行了大量的相关研究，涌现出众多针对非一致性水文频率分析的新方法和新理论，可以简单概括为间接法和直接法两大类。

间接法主要基于“还原或还现”思想，即将原始的非一致性水文序列经过一系列变换，使得序列重新满足一致性要求后再进行频率分析，有基于趋势分析和基于跳跃分析等非一致性分析方法［2-4］；直接法则主要有分解合成法［5］、混合分布法［6］、时变矩法［7］、条件概率分布法［8］、广义加法模型［9］等。 以上方法在我国各地区、各流域有着广泛的应用，如成静清等［10］将基于混合分布的非一致性频率分析方法应用于陕北及关中地区的实测年径流量序列处理中，研究表明理论频率和经验分布拟合较好；胡义明等［11］提出了基于跳跃分析的非一致性水文频率计算方法，并对金沙江流域某水文站资料进行了研究；谢平等［12］提出了一种基于小波分析的非一致性洪水频率计算方法，并在西江梧州站做了实例验证；刘丙军等［13］运用时变矩方法研究了西北江三角洲地区的非一致性洪水频率分析问题；李伶杰等［14］对条件概率模型在非一致性水文序列频率计算中的应用进行了研究，该研究为变化环境下的水文频率分析提供了新方法；张冬冬等［15］以GAMLSS模型为基础，分析了大渡河流域降水频率的非一致性特征，结果表明GAMLSS 模型可以很好地反映水文序列的非一致性特征。

1 研究对象和方法

以黄河流域上、中、下游的三大控制站（兰州站、花园口站、利津站）的年径流量时间序列为研究对象，在序列特性分析的基础上，采用不同方法进行各站的设计年径流量计算。 三大站从上到下分别为兰州水文站、花园口水文站和利津水文站，其中兰州水文站和花园口水文站具有1919—2018年共100 a 长度的年径流量资料，利津水文站有1952—2018年共67 a 长度的年径流量资料。

利用谢平等［16］提出的水文时间序列变异诊断系统对3 个站的年径流量时间序列进行变异诊断（见图1）。 如果研究序列存在变异特征，说明序列不满足一致性要求，则需采用非一致性频率计算方法来进行设计年径流量计算；如果序列不存在显著变异，说明序列保持着较好的一致性，则采用传统水文频率分析方法进行设计年径流量计算。

图1年径流量时间序列的变异诊断

2 研究过程

2.1 水文时间序列一致性诊断

（1）初步诊断。 综合利用过程线法和累计值法分别对兰州站、花园口站和利津站的年径流量序列进行一致性分析，这两种方法均属于直观的定性分析，因原理简单而被广泛应用于水文时间序列一致性的初步诊断中。 具体诊断结果如图2 所示。

图2 三大控制站年径流量序列一致性的初步诊断

由图2可见，1919—2018年兰州站和花园口站的年径流量序列变化趋势不明显，而利津站1952—2018年的年径流量序列呈现出较为明显的下降趋势；三大站的时序累计值结果显示，兰州站的年径流量序列与45°斜率直线的拟合效果最好，而花园口站和利津站的拟合误差则相对较大。 综合分析，可以初步确定花园口站和利津站年径流量序列的一致性可能遭到了破坏。

为了进一步准确地描述3 个水文站年径流量序列的一致性变化情况，需要进行详细诊断。

（2）详细诊断。 一般地，可以认为造成水文时间序列发生变异的主要原因是序列出现了趋势、跳跃和周期等成分。 由于目前我国绝大多数水文站的时间序列长度较短，较早建设的站也只有几十年的观测资料，因此周期成分一般不显著，可不予考虑。 下面仅对趋势性成分和跳跃性成分进行识别和检验。

分别采用相关系数法、线性趋势回归检验法、Spearman 秩次相关检验法以及Kendall 秩次相关检验法等［17］对兰州、花园口和利津3 个站的年径流量序列的趋势性成分进行识别和检验，显著性水平均取0.05，检验结果见表1。

表1 各站年径流序列的趋势性成分识别与检验结果

由表1 中的检验结果可以看出，兰州站和花园口站近100 a 来的年径流量序列变化的趋势性不显著；而利津站1952—2018年的年径流量序列则呈现出较为显著的趋势性成分，且表现为下降趋势。 以上结论与初步诊断结论一致，再次证明利津站的年径流量序列已不再具备一致性，存在趋势性变异，传统的一致性水文频率分析方法失效。

下面对兰州站、花园口站和利津站的历史年径流量序列进行跳跃性成分的识别与检验。 虽然常用的水文时间序列突变检验方法众多，但各方法的侧重点不同，最终的检测结果常有差异［18］。 本文主要采用检验结果较为一致的有序聚类分析、Lee-Heghinian 法以及Mann-Kendall 非参数检验法（M-K 法）对兰州站、花园口站和利津站的年径流量序列进行跳跃性变异诊断，结果如图3～图8 所示。

图3 基于有序聚类分析和Lee-Heghinian 法的兰州站年径流量序列跳跃性诊断结果

当显著性水平α取0.05时，兰州站年径流量序列有序聚类分析和Lee-Heghinian 法的统计量｜ T ｜=3.85＞tα／2=1.64，说明兰州站1919—2018年年径流量时间序列存在较为显著的突变点，最大可能变异位置为1932年；观察图4可以看出，M-K 法检测到了多个突变点，其中就包括了1932年。 综合以上两种方法的突变检验结果，确定1932年为兰州站年径流量序列的最大可能突变点。

图4 基于M-K 法的兰州站年径流量序列跳跃性诊断结果

当显著性水平取0.05 时，花园口站年径流量序列有序聚类分析和Lee-Heghinian 法的统计量为4.21，说明花园口站1919—2018年年径流量时间序列存在较为显著的突变点，最大可能变异位置为1990年；观察图6可以看出，M-K 法检测到的突变点也为1990年。综合以上两种方法的突变检验结果，确定1990年为花园口站年径流量序列的最大可能突变点。

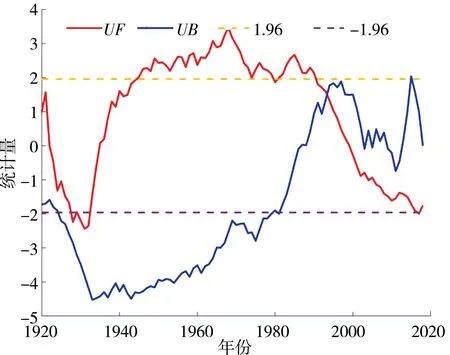
图6 基于M-K 法的花园口站年径流量序列跳跃性诊断结果

当显著性水平α取0.05时，利津站年径流量序列有序聚类分析和Lee-Heghinian 法的统计量｜ T ｜=5.04＞tα／2=1.64，说明利津站1952—2018年年径流量时间序列存在较为显著的突变点，最大可能变异位置为1985年和1990年；观察图8，可以看出M-K 法检测到的突变点为1985年。 综合以上两种方法的突变检验结果，确定1985年为利津站年径流量序列的最大可能突变点。

图7 基于有序聚类分析和Lee-Heghinian 法的利津站年径流量序列跳跃性诊断结果

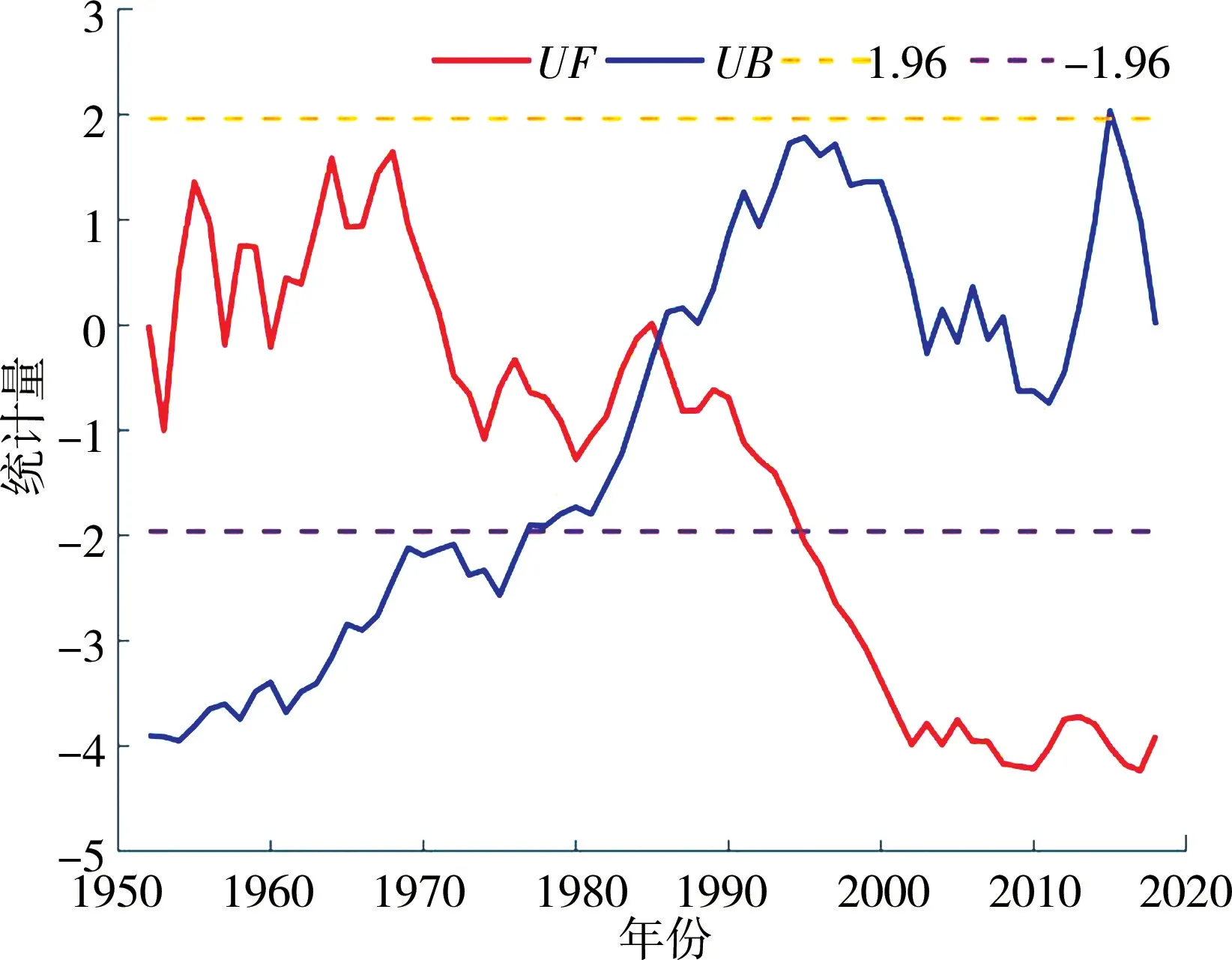
图8 基于M-K 法的利津站年径流量序列跳跃性诊断结果

综上，可以确定3 个水文站的历史年径流量序列均发生了变异，各序列不再满足一致性要求。 其中：兰州站和花园口站的年径流量时间序列主要发生了跳跃性变异，而利津站的年径流量时间序列既发生了趋势性变异又发生了跳跃性变异。 针对各序列的不同变异特性，分别采用相应的非一致性水文频率分析方法进行设计年径流量计算。

2.2 水文频率分析计算

2.2.1 兰州站年径流量序列频率分析

针对兰州站年径流量序列的跳跃性变异特征，采用基于跳跃诊断的二次修正法进行非一致性水文频率计算。 对于年径流量序列xi，假设变异点为τ，首先根据变异点位置将原始序列划分成前后两个子序列，即（x1，x2，…，xτ） 和（xτ＋1，xτ＋2，…，xn） 。可以得到将变异点之前的序列还原到变异点之后状态的表达式为

式中：Xt、St分别为修正前、后的变异点之前的子序列；Ex1、Ex2分别为原始序列变异点前、后两个子序列的均值。

对还现处理后的新序列进行一致性检验，若仍不满足一致性要求，则进行下一步处理。

如图9，修正后的序列变异强度虽然有所弱化，但仍然存在一定程度的跳跃特征，以1989年最为显著，故需要进一步处理以完全消除序列的跳跃特征。

图9 一次修正后的基于有序聚类分析和Lee-Heghinian 法的兰州站年径流量序列跳跃性诊断结果

对一次修正后的序列继续进行变异诊断，根据新的变异点位置将序列重新划分成两个子系列，均值仍然记为Ex1和Ex2，设Ex为平稳状态的振动中心，则有：

根据文献［3］，权重γ的计算公式以及二次修正后的序列可表示如下：

从图10可以看出，经过连续两次修正，兰州站的年径流量序列已经不再表现出突变特征（UF、UB曲线无交点），说明二次修正后的年径流量序列满足一致性要求。

图10 二次修正后的基于M-K 法的兰州站年径流量序列跳跃性诊断结果

对二次修正后的年径流量时间序列进行水文频率分析，以P-Ⅲ型曲线为分布线型，采用优化适线法计算均值、变差系数和偏态系数等参数，兰州站设计年径流量计算结果见表2。

表2 兰州站设计年径流量计算结果

2.2.2 花园口站年径流量序列频率分析

由图5、图6 的分析结果可知，花园口站年径流量序列的最大可能变异位置为1990年，则原序列被划分成1919—1990年和1991—2018年两个子序列。 两段序列的长度均能满足水文频率分析的要求，故宜采用混合分布法计算花园口站的设计年径流量。

图5 基于有序聚类分析和Lee-Heghinian 法的花园口站年径流量序列跳跃性诊断结果

混合分布法的主要思想是将非同分布的样本序列视作若干个子分布混合而成，实际应用中为简化计算，多将原始序列分解成两个子序列，并将各子序列占原始序列长度的比例作为权重系数进行连接。可用以下公式进行描述：

式中：F（x） 为混合分布函数；F1（x） 和F2（x） 分别表示变异点前、后序列的分布函数；β为变异点前的子序列占原始序列长度的比例。

以P-Ⅲ型曲线为分布线型，采用优化适线法计算P-Ⅲ型分布中的参数，分别对1919—1990年、1991—2018年两个年径流量子序列进行水文频率分析，再将各子序列的设计值进行叠加，即可得到原序列的设计值。 花园口站设计年径流量计算结果见表3。

表3 花园口站设计年径流量计算结果

2.2.3 利津站年径流量序列频率分析

由前述分析可知，利津站历史年径流量序列既存在着趋势性变异又存在着跳跃性变异。 为了更好地刻画出该序列的趋势性特征，本文采用分解合成法计算利津站的设计年径流量。

先对原始年径流量序列进行db3 小波分解，分解深度取6 级（d1～d6）。 如图11 所示，s为原始序列，原始序列被分解成了7 个部分，其中a6为序列的趋势项（单位为亿m3）。可以看出，趋势项序列呈现出较为明显的下降趋势，说明利津站1952—2018年年径流量有逐年减少的趋势，这一现象与前述分析结论也是一致的。

图11 利津站年径流量序列的db3 小波分解结果

一般把趋势项看作是原始序列的确定性成分，而把趋势项以外的其余部分视作随机性成分，并假定随机性成分仍保持着一致性。 对确定性成分进行函数趋势拟合，根据得到的拟合方程计算未来年份的设计值（见图12）；对随机性成分的设计值采用传统的一致性水文频率分析方法进行计算（见表4）。

图12 确定性成分的线性拟合结果

表4 利津站年径流量随机性成分序列设计值

将确定性成分的分析结果和随机性成分的计算结果进行叠加合成，即可得到利津站各频率的设计年径流量。 为了体现出年径流量序列隐含的趋势特征，表5 给出了过去情景下（2010年）、现状情景下（2020年）和未来情景下（2030年）的年径流量设计值。

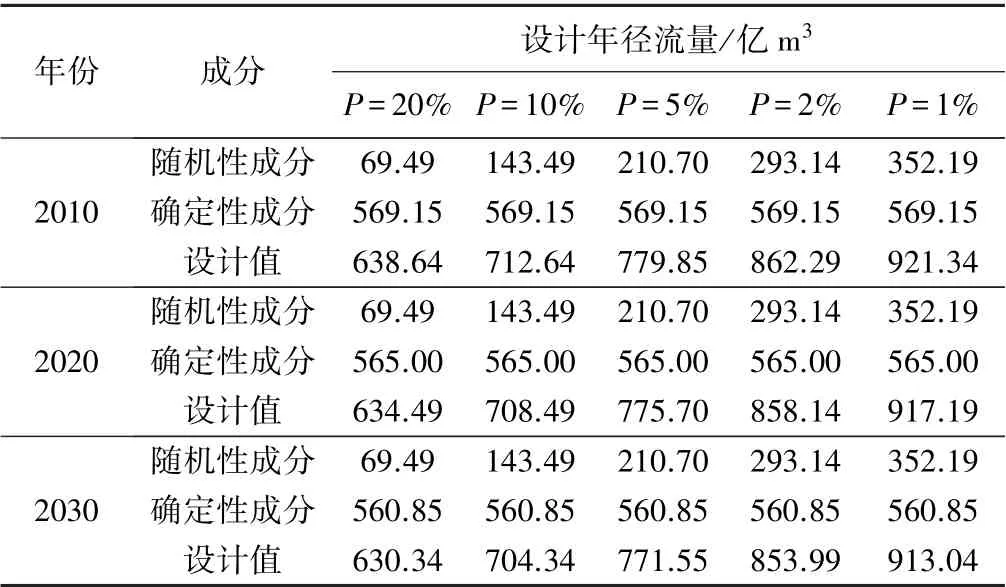
表5 利津站在不同情景水平年下的年径流量设计值

3 结论

（1）经初步诊断和详细诊断，3 个水文站的年径流量序列均不满足一致性要求，无法直接进行水文频率分析。 其中：兰州站和花园口站均存在显著的跳跃性变异，变异位置分别为1932年和1990年；利津站既存在趋势性变异又存在跳跃性变异，整体上年径流量序列呈现下降趋势，最大可能突变位置为1985年。

（2）根据3 个水文站年径流量序列的变异特点，分别采用不同的非一致性频率计算方法，包括基于跳跃诊断的二次修正法、混合分布法和分解合成法，计算得到各水文站不同重现期的设计年径流量。

（3）经计算，兰州站和花园口站的百年一遇设计年径流量分别为498.51 亿m3和852.14 亿m3，利津站在3种不同情景下的百年一遇设计年径流量分别为921.34 亿、917.19 亿、913.04 亿m3。