摇杆操控型农机转向控制策略

张 宇， 李志伟， 赵建贵， 蒿晟昆

（山西农业大学农业工程学院，山西 晋中 030801）

0 引言

大型电动农机在田间作业存在能源与动力问题，致使其实际应用中未能大面积普及，而小型电动农机具有结构简单、清洁节能、作业周期长、使用便捷和噪声小等优点，目前已在部分地区展开使用[1-6]。小型电动农机在结构方面，体积小、质量小、结构简单、简化底盘结构及分布合理；在动力方面，采用分布式驱动模式驱动永磁直流减速电机；在能源方面，利用电能作为供电能源，具有清洁节能的优点[7-11]。针对温室与茶园等复杂地形下，采用永磁直流减速电机作为小型电动农机的驱动装置，该型农机配套不同农具应用于田间和设施温室实施，完成耕作、旋耕和播种等基础作业，通过配备智能化装备可实现自动导航、果蔬采收和运输等工作，是当代智能农机的研究热点[12-15]。

赵艳娥等[16]建立了电动汽车的差速控制模型，在车辆转弯行驶情况下，考虑轴荷转移、车轮偏转角和向心力等影响因素，利用Matlab/Simulink 软件对其进行仿真。靳彪等[17]针对四轮电机驱动电动汽车，对其各个工作部件进行了分析，依据样车的基本参数，利用Matlab/Simulink 软件建立了有7 自由度四轮电机驱动电动汽车的仿真模型，同时建立仿真模型，根据加速踏板变化，建立了加速意图模型，并利用非线性回归方法中的三角形三次插补法建立了轮毂电机模型。徐寅等[18]针对电动汽车的传动系统结构与电动汽车的差速控制系统进行了探讨，详细介绍了差速控制原理，以车轮转速与转矩作为控制变量，进行了研究分析。

本研究根据小型电动农机对实际工作环境的需求，利用永磁直流减速电机设计了摇杆操控型电动农机。针对摇杆电压、车轮转速和导向轮转向偏角间的关系进行分析，根据摇杆电压计算车轮转速与导向轮转向偏角，建立“电压−转速”与“电压−转向”模型，借鉴电子差速控制原理，从而完善小型电动农机差动理论可行性及特性的论证过程，为后续控制器的优化奠定了基础。

1 结构设计

摇杆操控型电动农机主要由永磁直流减速电机、电动推杆、控制器和铅酸锂电池组成，如图1 所示。永磁直流减速电机的功率为650 W，分别安装于后驱动轮；电动推杆安装于导向轮内侧，通过电动推杆的伸缩控制转向偏角；控制器由主控芯片STM32F103F103Z8T6、电机驱动芯片IR2103S 和摇杆电路构成，以电子差速原理控制农机的行进速度与转向；采用48 V 铅酸锂电池作为动能对整个装备的各个工作部件提供动力[19]。小型电动农机各个模块进行相互配合，实现农机的各项功能。

图1 摇杆操控型电动农机装备结构Fig. 1 Structure of rocker-operated electric agricultural machinery equipment

2 工作原理

2.1 电子差速原理

两轮差速控制策略应用于小型电动农机上，前轮作为导向轮，控制行驶方向，后轮作为驱动轮，提供行驶动力。小型电动农机在其转向时，由摇杆摆动输出的电压可获得两驱动轮的转速，由于两驱动轮速度不同，可以实现电子差速，从而实现转向目的[20-21]。

小型电动农机直线行驶时，由于永磁直流减速电机直接与车轮相连，永磁直流减速电机的转子旋转角速度等于车轮角速度，由于小型电动农机的车轮滚动半径相等，则可以得到式（1）

式中Ww,r，Ww,l−小型电动农机左右驱动轮的旋转角速度，rad/s

当小型电动农机直线行驶时，两个驱动轮不需要差速，此时两个驱动轮的转速相等。

当小型电动农机转向时，摇杆的转角δ≠0°，当小型电动农机的车轮转速不均匀时，导致小型电动农机转向时出现故障，车轮可能会与地面发生平移滑动现象，加快车轮的磨损，减少使用寿命。假设小型电动农机在转向时，所有的车轮均作滚动运动，不产生平移滑动，内侧车轮转向偏角要大于外侧车轮转向偏角，在小型电动农机低速转向行驶过程中，结合Ackermann &Jeantand 模型进行设计，建立摇杆操控型电动农机转向模型，如图2 所示。

图2 摇杆操控型电动农机转向模型Fig. 2 Steering model of rocker-operated electric agricultural machinery

小型电动农机转向时，由摇杆的转角作为输入，控制器将输入信号进行计算，将解析出的驱动轮转速信号发送给电机控制器，通过车轮的不同转速，实现差速控制。

前轴与后轴的转弯半径和导向轮转向偏角的函数关系为

根据小型电动农机的运动方式，可以分为以下3 种情况。

（1）当Vr−Vl= 0，即小型电动农机左右驱动轮的转速大小相等，行驶方向与线速度方向相同，小型电动农机的质心CG处的线速度V=Vr=Vl，车身转弯半径可以表示为R′→∞，此时小型电动农机做直线运动。

（2）当Vr+Vl= 0，即小型电动农机左右驱动轮的转速大小相同，但是方向相反，小型电动农机的车体质心CG的线速度V= 0 ，转弯半径可以表示为R′=0，此时小型电动农机绕其质心CG转动，即小型电动农机可以实现原地转向。

（3）当Vr±Vl≠ 0 时，即小型电动农机左右驱动轮的转速大小不相等，且有多种情况，小型电动农机的车体质心CG线速度为V= (Vr+Vl)/2，转弯半径可以表示为Rr，此时小型电动农机围绕一固定点做半径为Rr的转向运动。

根据小型电动农机实际应用过程中3 种运动规律，通过摇杆电压控制电动农机左右驱动轮的转速，可进行任意角度转向。应用电子差速控制算法对摇杆输入信号进行处理，保证摇杆输入信号的准确性，进而保证小型电动农机运行的稳定性。

2.2 摇杆操控工作原理

摇杆工作原理是通过将一块通有电流的导体放置于磁场区域，导体两端会产生电压UH，其被称为霍尔电压，如图3 所示。当导体放置在空间某一位置时，霍尔电压UH，导体厚度b与磁感应强度B间关系为

图3 霍尔效应原理Fig. 3 Hall effect schematic

式中RH−霍尔系数，只与所选导体的固有特性有关

UH−霍尔电压，V

φ−导体所在区域下的磁场与垂直方向所形成的夹角，（°）

B´−磁感应强度，表示导体所在磁场区域下垂直于导体平面的磁场强度，T

IH−通过导体的电流，A

B−所选取导体厚度，mm

根据摇杆的工作原理，在磁场一定的情况下，摇杆的端点距中心位移l与所在磁场强度B间关系为

通过霍尔传感器可以测得导体垂直方向的磁场强度，就可以计算出遥控杆端点距中心点的位移。

对l进行积分

由式（11）可知，摇杆端点的位移l与霍尔电压UH成正比。

根据摇杆端点G的运动轨迹，可以得到近似的半个球面，利用空间直角坐标系来绘制运动轨迹，如图4所示。已知遥控杆的杆长为c，因此运动轨迹是以c为球半径的半球面，其中任一点G将其投影在xoy平面上，所得到的投影点为点G´，点G´的坐标可以表达为（csinφsinθ ，csinφcosθ ）， φ为z轴与摇杆间的夹角，（°），夹角的取值范围是 0°≤φ ≤30°； θ为在xoy平面上点G´与y轴正方向间夹角，（°），夹角的取值范围是0°≤θ ≤360°。将所有点投影在xoy平面上，投影点G´在xoy平面将会形成的投影区域，如式（12）所示。

图4 摇控杆作用原理Fig. 4 Action principle of remote control lever

根据摇杆的左右摆动，与差速控制策略相匹配，对其进行了稳定性分析，实现了对操控信号的采集，控制芯片对数据进行处理，获得行驶速度与车身转向偏角。

3 摇杆“电压−转速”模型

3.1 摇杆电压分量

假设车轮转速的取值范围在0～V0，根据霍尔传感器所产生的电压值建立一个关系，由这个关系可以求得一个确定比例。当摇杆没有任何变化时，保持于中心位置，此时霍尔传感器产生的电压值为UH0；当摇杆在OG´方向运动，此时处于极限位置，霍尔传感器产生的电压值为UHmax，根据正交分解原理，可将所得电压分解为两组电压值Ux、Uy，V，表示为

3.2 “电压−转速”模型

根据式（13）和式（14）可知，摇杆的变化可以将其分解为Ux、Uy两个信号分量，Ux表示为小型电动农机转向控制信号，Uy表示为小型电动农机前进或后退的速度控制信号。小型电动农机的运动方向与速度大小可由Ux、Uy两个信号分量合成。

假设左右电机转速分别为Nr、Nl，r/min，建立Nr、Nl与Ux、Uy的模型。

左轮转速与摇杆电压间的关系

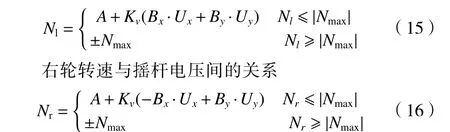
式中KV−小型电动农机调挡系数

Bx−左右转向控制系数

By−前后方向控制系数

Nmax−最大速度上限值

A−修正常数

通过拟合可得“电压−左轮转速”模型为

采用非线性曲面拟合的摇杆电压−左轮转速曲面如图5 所示。

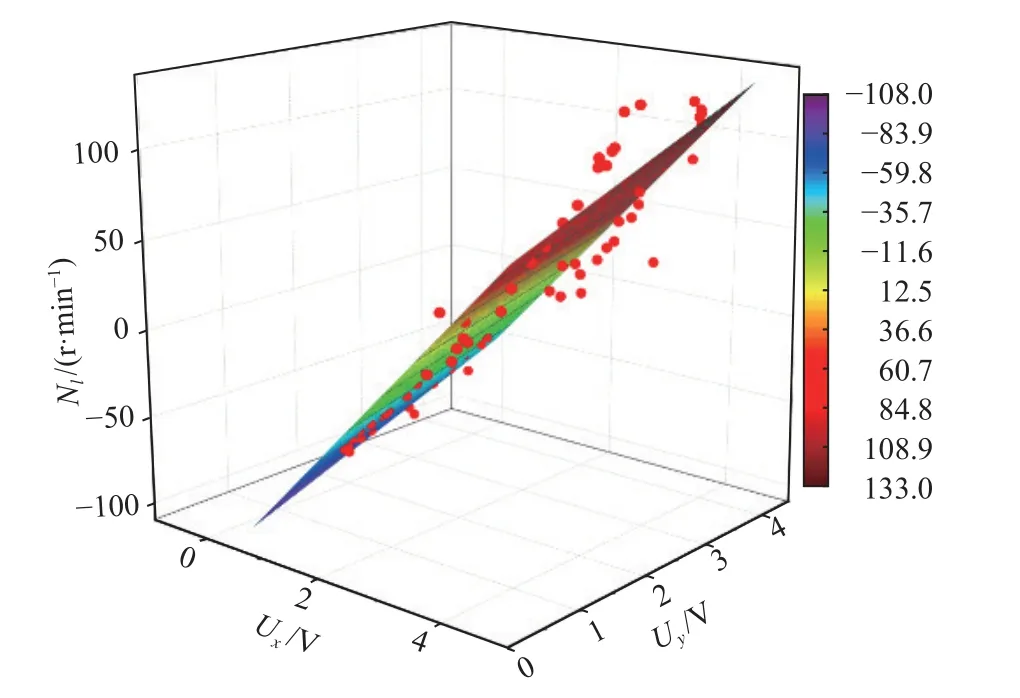
图5 “电压−左轮转速”拟合Fig. 5 Fitting of "voltage-left wheel speed"

通过拟合可得“电压−右轮转速”模型为

采用非线性曲面拟合的摇杆电压−右轮转速曲面图如图6 所示。

图6 “电压−右轮转速”拟合Fig. 6 Fitting of "voltage-right wheel speed"

Bx、By表示方向控制系数，通过调试得到最佳值，获得最好的操作性能。KV表示调挡系数，小型电动农机具有5 个挡位，通过挡位的调节，可以获得更大的速度上限。

左右轮转速与摇杆电压在一定范围内基本成线性关系，任一点的电压，经过正交分布分解为Ux和Uy，可求得车轮左右轮线速度Nr和Nl，Nr代表小型电动农机右轮的转速，Nl代表小型电动农机左轮的转速。

采用非线性拟合方式，Adj R-square 校正决定系数决定拟合效果，“电压−左轮转速”与“电压−右轮转速”拟合结果分别达到了0.954 6 与0.974 4，同时COD（R2）分别可以达到0.955 8 与0.975 0，拟合效果稳定，该方法拟合出的车轮转速处于试验所得的不同电压下的转速范围之内，根据摇杆摆动的位置与所处挡位大小，通过摇杆电压与左右两轮转速之间的数学模型，可得到两驱动轮的转速。

4 摇杆“电压−转向”模型

4.1 摇杆电压与车身偏角

目前传统的插值方法在使用过程中，在进行插值函数时，会产生较高的次数，运算也将变得更加的复杂。同时，在进行插值函数过程中，可能由于一些错误数据，会导致试验结果出现较大误差。而采用曲线曲面拟合法可以有效地解决插值方法的缺陷。采用非线性曲面拟合方法，根据试验所采集的数据，建立δ与Ux和Uy之间的模型。

假设实际试验点数据（δi，Uxi，Uyi）（i=1，2，...，n），可得曲面拟合函数为

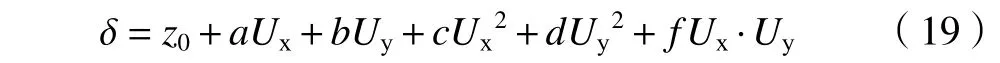
式中Ux−自变量，小型电动农机转向控制信号

Uy−自变量，小型电动农机前进或后退的速度控制信号

δ−拟合函数，小型电动农机的车身转向偏角

z0、a、b、c、d、f−拟合函数中的待定系数，曲面拟合函数由待定系数唯一确定

通过拟合可得模型为

采用非线性曲面拟合的摇杆电压−车身转向偏角曲面如图7 所示。

图7 “电压−转向”拟合Fig. 7 Fitting of "voltage-steer"

由图7 可知，当Ux= 2.5、Uy= 2.5 时，车身转向偏角为0°，且农机处于静止状态。

当2.2＜Uy＜2.8、2.2＜Ux＜2.8 时，车身转向偏角为0°，且摇杆电压处于死区，农机没有动作，电压死区可以保证摇杆在发生轻微变化时，农机保持静止状态。

当Uy＜2.2、Ux＜2.2 时，随着Uy、Ux方向上的减小，δ将逐渐增大，农机导向轮向左转向，行驶方向为反向，同时随着Uy的减小，农机反向行驶将逐渐加快。

当Uy＞2.8、Ux＜2.2 时，随着Uy方向上的增大，Ux方向上的减小，δ将逐渐减小，农机导向轮向左转向，行驶方向为正向，同时随着Uy的增大，农机正向行驶将逐渐加快。

当Uy＜2.2、Ux＞2.8 时，随着Uy方向上的减小，Ux方向上的增大，δ将逐渐减小，农机导向轮向右转向，行驶方向为反向，同时随着Uy的减小，农机反向行驶将逐渐加快。

当Uy＞2.8、Ux＞2.8 时，随着Uy、Ux方向上的增大，δ将逐渐增大，农机导向轮向右转向，行驶方向为正向，同时随着Uy的增大，农机正向行驶将逐渐加快。

采用非线性拟合方式，Adj R-square 校正决定系数决定拟合效果，拟合结果达到了0.869 0，同时COD（R2）可以达到0.877 3，拟合效果稳定，该方法拟合出的车身转向偏角处于试验所得不同电压下的转向偏角范围内，能够较好地反映出摇杆“电压−转向”偏角性。

4.2 车身偏角与导向轮偏角

车身转向偏角与导向轮内外车轮转向偏角之间的关系成正比，如图8 和图9 所示。

图8 车身转向偏角−导向轮内车轮转向偏角关系Fig. 8 Relationship between steering angle of body and steering angle of wheel inside guide wheel

图9 车身转向偏角−导向轮外车轮转向偏角关系Fig. 9 Relationship between steering angle of body and steering angle of outer wheel of guide wheel

车身转向偏角与内车轮转向偏角的关系

车身转向偏角与外车轮转向偏角的关系

式中 δin−内车轮转向偏角，（°）

δout−外车轮转向偏角，（°）

δ−整车转向偏角，（°）

4.3 转向控制方式

通过采集摇杆电压作为输入值，将其传递给控制器，控制器进行数据分析，通过非线性拟合方式求得车身转向偏角，根据车身转向偏角与导向轮内外车轮转向偏角之间的关系，建立数学模型，控制器进行算法分析，解析电动推杆的行程量，通过改变电动推杆的伸缩量，带动导向轮进行偏转，从而控制摇杆操控型农机按照驾驶者的意图进行转向。

5 结束语

对摇杆操控型农机的转速与转向展开深入研究，应用电子差速控制原理，通过摇杆电压作为输入量，以驱动轮转速作为输出量，建立“电压−转速”模型，控制车轮转速大小。通过摇杆电压作为输入量，以车身转向偏角为控制目标，建立“电压−转向”模型，拟合出车身转向偏角，根据车身与导向轮转向偏角间的关系，计算出导向轮转向偏角。拟合结果表明，电子差速控制策略可以使车辆在转向行驶过程中，车辆的转向角在最佳范围内，保证车辆行驶的稳定性。

此类农机可以解决大型农机在复杂环境下，由于体积过大，导致无法实现机械作业的问题。小型电动农机凭借环保、操作便捷等优点得到广泛的应用，同时对于农业的发展有着重要意义，对于农业机械的发展也起到了促进作用。