胶园植保硫磺粉颗粒离散元模型参数标定
李承明,张 斌,2,夏雨阳,王 勇,肖 骁,付 威*
(1.海南大学 机电工程学院,海南 海口 570228;2.海南大学 信息与通信工程学院,海南 海口 570228)
【研究意义】天然橡胶是我国重要的战略物资和工业原料,广泛应用在国民经济建设中[1]。我国天然橡胶树的种植面积超过113 万hm2,其中海南省种植面积超53 万hm2。白粉病是我国橡胶树所面临最严重的病害之一,因此防治白粉病是天然橡胶生产管理过程中的重要环节之一[2]。目前白粉病主要通过人工背负式喷粉机进行硫磺粉喷施作业,防治效果直接影响到天然橡胶的品质和产量。硫磺粉作为胶园植保机械化喷施作业过程中的重要组成部分,其接触特性对喷粉机的喷施效果有重要影响[3]。因此,研究硫磺粉颗粒的离散元参数对胶园植保喷粉机械的优化设计有重要意义。【前人研究进展】国内外学者应用离散元法(Discrete Element Method,DEM)对不同的农业物料颗粒进行了大量参数标定方面的研究[4-6]。王韦韦等[7]以实际堆积角为目标值,对玉米秸秆粉料进行了致密成型离散元仿真模型参数标定研究;李永祥等[8]通过颗粒缩放将小麦粉颗粒放大至1.2 mm后,再对小麦粉的接触参数进行标定,仿真结果与实际值无显著性差异,为小颗粒的参数标定提供了参考。石辰风等[9]将四种中药浸膏粉颗粒进行放大后,根据仿真模拟休止角,确定了相应的接触参数;邢洁洁等[10]为了获取适用于海南热区砖红壤与农业机械工作部件之间的离散元参数,对香蕉地试验田的砖红壤样品进行了模型参数标定,并加以破土阻力试验验证;王黎明等[11]通过物理堆积试验与仿真相结合,对猪粪接触参数做了标定工作;袁全春等[12]通过仿真试验建立模型,结合圆筒提升法进行目标参数寻优,标定了有机肥离散元模型参数;武涛等[13]基于土壤堆积角物理试验,采用Hertz-Mindlin with JKR 接触模型进行仿真试验,获得了较高可信度的黏性土壤离散元接触模型参数。综上可知,应用离散元法获得散体物料相关参数的方式得到广泛地认可,具有良好的可行性。【本研究切入点】针对胶园植保硫磺粉颗粒接触参数的研究未见有相关报道。主要由于硫磺粉的颗粒粒径为微米级,且颗粒间易发生粘结,接触特性复杂,使用常规的手段不易准确获得其相关接触参数,需要通过虚拟标定来确定。【拟解决的关键问题】以胶园植保硫磺粉为研究对象,采用Hertz-Mindlin with JKR 接触模型,依次进行Plackett-Burman试验、最陡爬坡试验和Box-Behnken试验,求解最优参数组合,对比仿真休止角与实际硫磺粉休止角完成离散元模型参数标定,以期为研究硫磺粉颗粒与喷粉装置之间的相互作用机理提供有效基础参数。
1 材料与方法
1.1 试验材料与仪器
试验材料选用广西防城港五星环保科技股份有限公司生产的硫磺粉,含水率为9%,细度为325 目(粒径45 μm);试验仪器为粉体综合特性测试仪(型号:BT-1000型,丹东百特仪器有限公司)。
1.2 休止角测量
休止角被广泛用于表征颗粒物料的流动性,也称为堆积角、安息角。通过BT-1000型粉体综合特性测试仪进行漏斗法测量硫磺粉休止角,测试仪器如图1所示[14]。将接料盘和休止角试验台放置在测试仪固定位置,从入料口添加硫磺粉后,在振动筛的作用下通过筛网、出料口洒落到试样台上,形成锥体。待锥体稳定后,关闭电源,将量角器慢慢靠近硫磺粉锥体,调整好角度和位置后,开始测定休止角的大小,如图2所示。为保证测量的准确性,需要分别在3个不同的位置对休止角进行测定,取其平均值,试验重复3次,最后得到硫磺粉的实际休止角平均值为48.56°。

图1 BT-1000型粉体综合特性测试仪Fig.1 BT-1000 powder comprehensive characteristic tester

图2 测量休止角Fig.2 Measuring the repose angle
2 仿真模型
2.1 接触模型选取
硫磺粉颗粒间存在的范德华力和静电力等黏附力,导致了硫磺粉的黏附和团聚[15-16],因此选择EDEM 2018 软件中的Hertz-Mindlin with JKR 接触模型进行仿真,该模型适用于模拟颗粒间因作用力而发生粘结和团聚的情况[17-18],本文通过引入JKR表面能用于表征硫磺粉颗粒间的接触。
2.2 仿真参数设置
由于硫磺粉颗粒粒径微小,本征参数难以准确获取,综合参考粉体颗粒离散元仿真相关文献[19-22],设定硫磺粉颗粒的本征参数为:真实密度2 000 kg/m3、泊松比0.3、硫磺粉剪切模量5×107Pa。同时,结合EDEM 2018软件中内置的GEMM数据库,确定了硫磺粉颗粒与不锈钢之间仿真参数的参考范围,如表1所示。

表1 离散元参数范围表Tab.1 Parameter range table of discrete element method
2.3 仿真模型建立
在Creo软件中建立测量仪器的简化模型,另存为IGS格式,导入EDEM 2018软件中,仿真模型如图3所示。由于试验所用硫磺粉细度为325 目,颗粒形状接近球形,因此仿真采用球形颗粒模型。参考采用颗粒缩放法的国内外文献[8-9,23-25],选择放大颗粒直径设置为0.9 mm,如图4所示,颗粒生成方式为Dynamic,生成速率设为5 000 个/s,生成数量设为不限,仿真时间设置为5 s,时间步长设置为Rayleigh时间步长的20%,每0.05 s 保存1 次。待接料盘上的粉体颗粒锥体形状基本不变后,将生成速率设置为0 个/s继续仿真,待漏斗中颗粒落完并保持稳定后,采用软件后处理中自带的量角器工具,测量休止角。

图3 测量仪器简化模型Fig.3 Simplified model of measuring instrument

图4 仿真颗粒模型Fig.4 Simulation particle model
3 仿真试验与结果分析
3.1 Plackett-Burman试验
通过Plackett-Burman 试验以硫磺粉休止角为响应值,将7 个离散元参数分别用字母A到G进行表示,根据表1中的参数范围来设置各参数的高低水平,以参考范围的最低值为依据设定低水平的值,以参考范围的最高值为依据设定高水平的值,从而进行响应值与参数之间的显著性筛选。设定参数的高低水平后进行筛选试验,如表2所示。
使用Design Expert 8.0.6软件进行Plackett-Burman试验,按照表2中设定的参数依次输入,得到12组试验组合,依次利用EDEM 2018 软件进行仿真试验,测量休止角大小并填写表3,其中H、J、K、L为空白列。进一步地,继续使用Design Expert 8.0.6软件进行显著性分析,获得对休止角影响显著的参数排序,如表4所示。由表4可知,C(硫磺粉-硫磺粉滚动摩擦系数)的P<0.01,对硫磺粉颗粒休止角的影响极显著;F(硫磺粉-不锈钢滚动摩擦系数)和G(JKR 表面能)的P<0.05,对硫磺粉颗粒休止角的影响显著,其余的4个参数P>0.05,对硫磺粉颗粒休止角的影响较小。考虑到后续的试验影响,只选取对休止角影响性最大的3个参数。对于显著性较小的参数,结合国内相关文献取值如下:硫磺粉-硫磺粉恢复系数为0.2,硫磺粉-硫磺粉静摩擦系数为0.6,硫磺粉-不锈钢恢复系数为0.2,硫磺粉-不锈钢静摩擦系数为0.5。

表2 Plackett-burman试验参数Tab.2 Parameters of Plackett-Burman test

表3 Plackett-Burman试验设计及结果Tab.3 Design and results Plackett-Burman experiment

表4 Plackett-Burman试验参数显著性分析Tab.4 Significance analysis of Plackett-Burman test parameters
3.2 最陡爬坡试验
从上述的Placket-Burman试验可得,对硫磺粉休止角影响最大的3个显著性参数依次为:硫磺粉-硫磺粉滚动摩擦系数、JKR表面能和硫磺粉-不锈钢滚动摩擦系数。根据以上3个参数的高低水平值,选取适当的爬坡步长值,设计最陡爬坡试验,定位最优的参数区间。如表5 所示,共进行6 次试验,分别以0.05、0.1 和0.01 的爬坡步长确定显著性参数的取值后,进行休止角仿真试验。分析可知,第3 组试验的休止角相对误差最小,且整个最陡爬坡试验的相对误差呈现出先减少后增大的趋势。因此,最优的参数区间在第3组试验附近,可分别选取第2组和第4组的参数值为低、高水平进行下一步的Box-Behnken试验设计。
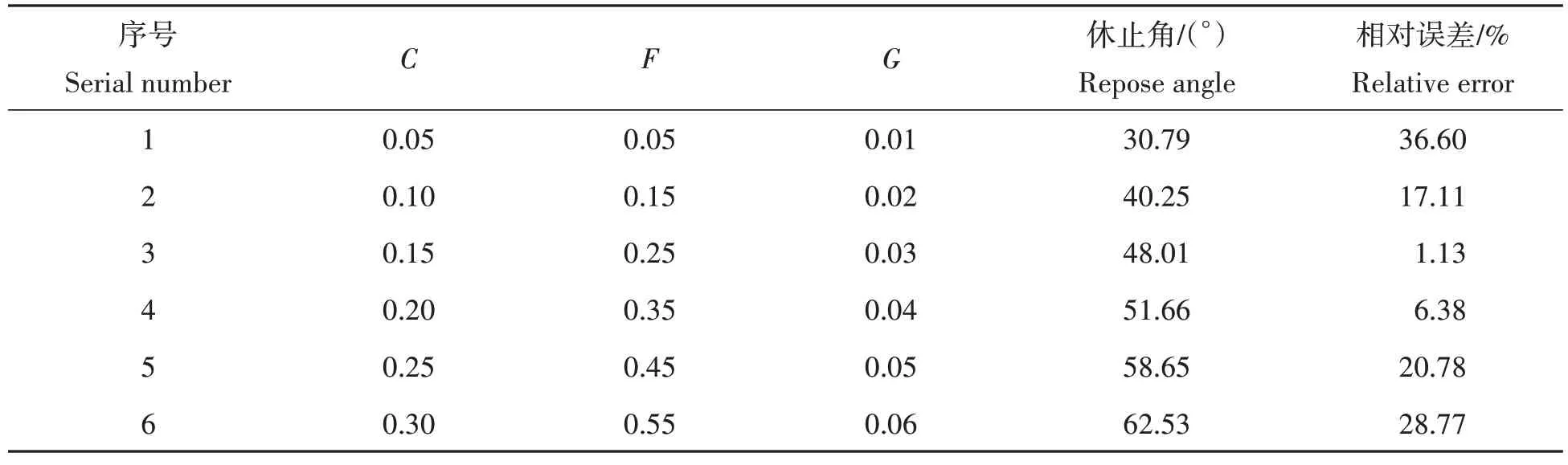
表5 最陡爬坡试验设计及结果Tab.5 Design and results of the steepest climbing test
3.3 Box-Behnken试验
获得休止角显著影响参数后,应用Box-Behnken 试验进行响应面分析并寻求最优解,以C(硫磺粉-硫磺粉滚动摩擦系数)、F(硫磺粉-不锈钢滚动摩擦系数)、G(JKR 表面能)为试验参数,休止角为指标进行试验,试验方案及结果如表6所示。
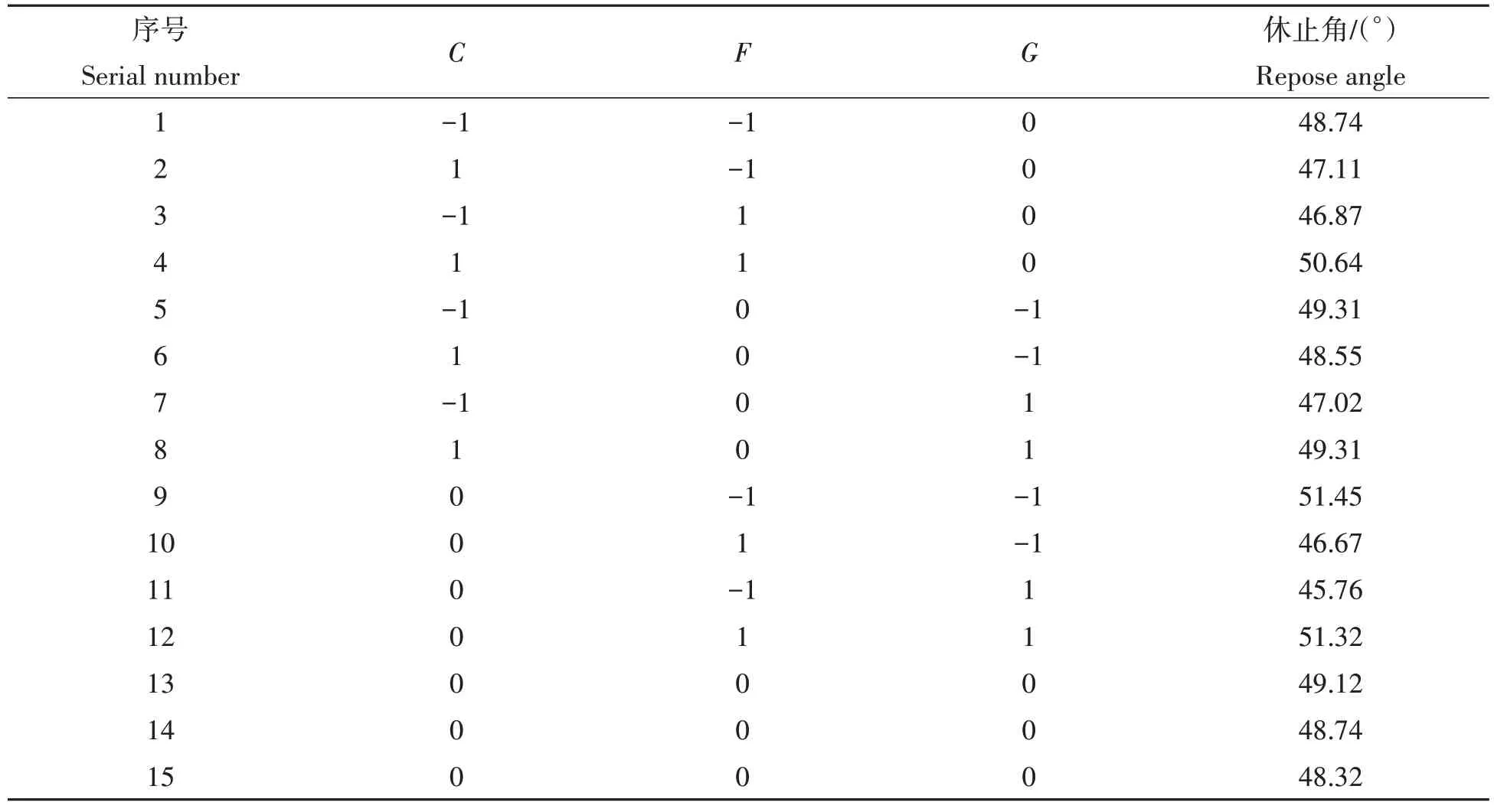
表6 Box-Behnken试验设计及结果Tab.6 Design and results of Box-Behnken test
表7为BoxBehnken试验模型方差分析,从表中可得,该拟合模型P=0.000 3(P<0.01),拟合度较好;其中C(硫磺粉-硫磺粉滚动摩擦系数)、CF(硫磺粉-硫磺粉滚动摩擦系数与硫磺粉-不锈钢滚动摩擦系数交互项)、CG(硫磺粉-硫磺粉滚动摩擦系数与JKR 表面能交互项)、FG(硫磺粉-不锈钢滚动摩擦系数与JKR表面能交互项)的P值均小于0.01;F(硫磺粉-不锈钢滚动摩擦系数)和G(JKR表面能)的P值均小于0.05,说明上述的参数都对休止角的大小有不同程度的影响,证明所得回归模型的有效性。此外,表中的失拟项P=0.791 9>0.05、决定系数R2=0.987 8、校正决定系数R2adj=0.965 9、变异系数CV 为0.65%、试验精确度Ap=22.657,说明所得模型具有良好的拟合性和精确度,与实际试验之间的误差较小,能够准确地反映出实际情况,表明了BoxBehnken试验具有较高可靠性。
表7 中的结果为基础,去除对休止角影响不显著项:C2、F2、G2后,优化二次回归模型,得到的方差分析结果如表8 所示:失拟项P=0.693 6;变异系数CV=0.72%;决定系数R2=0.975 8;校正决定系数R2adj=0.957 6;试验精密度Ap=24.275。不难看出,模型在拟合性、可靠性和精确性方面都表现良好,较优化前相比有一定程度的改善,在Design-Expert 8.0.6软件中建立显著性参数与休止角的优化后回归方程为:

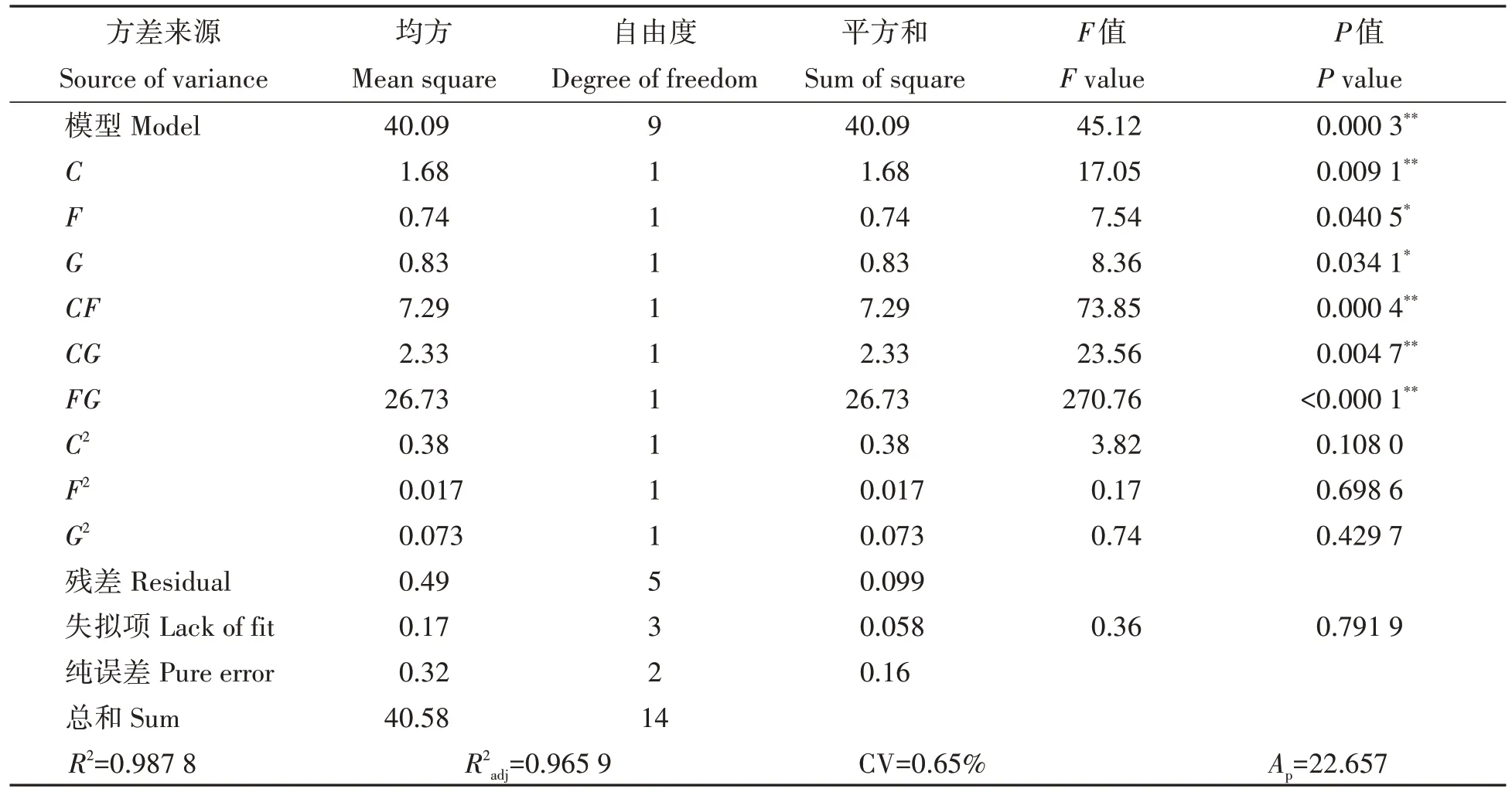
表7 Box-Behnken试验二次回归模型方差分析Tab.7 Anova of quadratic polynomial model of Box-Behnken test
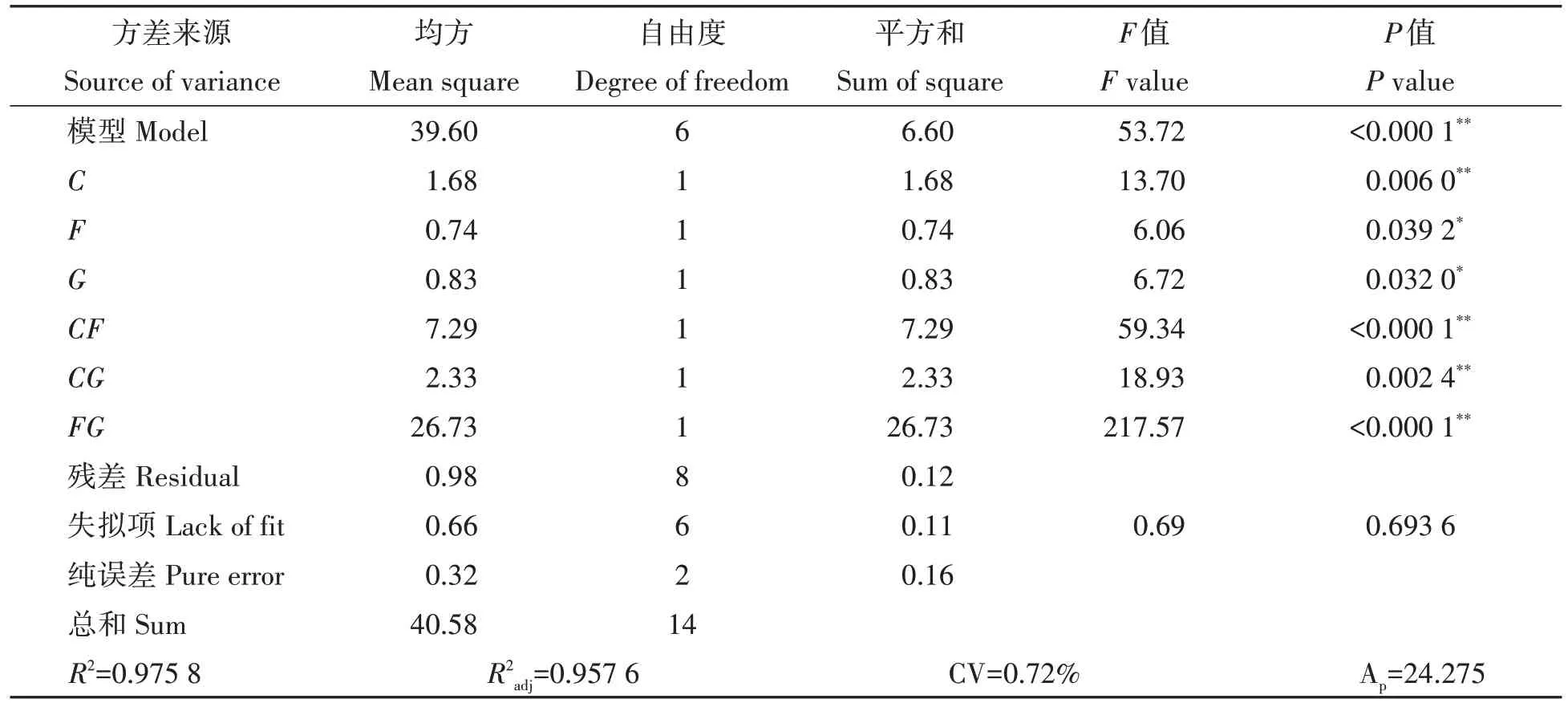
表8 Box-Behnken试验优化回归模型方差分析Tab.8 ANOVA of modified model of Box-Behnken test
4 参数优化与试验验证
利用Design Expert 8.0.6软件中的优化模块,以物理试验休止角平均值48.56°为目标值,对回归模型进行寻优,得到一组与物理试验数据相近的参数:硫磺粉-硫磺粉滚动摩擦系数0.17、硫磺粉-不锈钢滚动摩擦系数0.34、JKR 表面能0.03 J/m2,其余非显著性参数的取值结合相关文献(硫磺粉-硫磺粉恢复系数0.2,硫磺粉-硫磺粉静摩擦系数0.6,硫磺粉-不锈钢恢复系数0.2,硫磺粉-不锈钢静摩擦系数0.5)。为检验最优参数组合的准确性,将上述各参数值输入EDEM 2018 软件中进行仿真,得到结果如图5 所示。重复3次仿真试验,所得硫磺粉休止角分别为47.93°、47.77°、48.15°,平均值为47.95°,最优参数组合下休止角仿真结果与实际物理休止角结果的相对误差为1.26%,如图6 所示,仿真结果与真实试验在角度方面无明显差异。
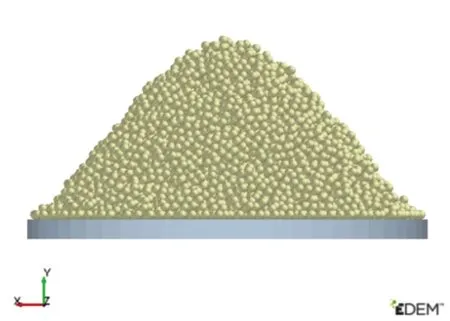
图5 仿真试验Fig.5 Simulation test

图6 物理试验Fig.6 Physical test
5 结论
通过BT-1000 型粉体综合特性测试仪进行硫磺粉休止角测定,得到硫磺粉的实际休止角平均值为48.56°。基于离散元软件EDEM 中Hertz-Mindlin with JKR 接触模型对放大颗粒的接触参数进行标定,由Plackett-Burman 试验可知,对硫磺粉休止角影响显著的参数为硫磺粉-硫磺粉滚动摩擦系数、硫磺粉-不锈钢滚动摩擦系数和JKR 表面能。根据Box-Behnken 试验结果,建立并优化3个显著性参数与休止角间的二次回归模型,根据模型方差分析的结果可知,除了3 个显著性参数(硫磺粉-硫磺粉滚动摩擦系数、硫磺粉-不锈钢滚动摩擦系数和JKR 表面能)的一次项外,各显著性参数的交互项对硫磺粉放大颗粒休止角影响也极其显著。
本文以硫磺粉实际休止角为目标值,进行寻优,求得显著性参数的最佳组合为:硫磺粉-硫磺粉滚动摩擦系数0.17、硫磺粉-不锈钢滚动摩擦系数0.34、JKR 表面能0.03 J/m2。进行对比试验,测得仿真试验的休止角为47.95°,与实际物理休止角的相对误差为1.26%,表明标定的硫磺粉离散元仿真参数有效。

