m-半格中的滤子及其相关拓扑性质

苏子祺, 赵 彬

(陕西师范大学 数学与统计学院, 西安 710119)

m-半格是一个重要的代数结构, 其将并半格的结构和半群的乘法运算相结合, 从而剩余格、 Frame,Quantale和格序半群等都是特殊的m-半格. Rosenthal[1]指出每个凝聚式Quantale都同构于某个含最大元的m-半格的理想之集构成的Quantale; 文献[2]在m-半格上定义了(素)模糊理想, 讨论了(素)模糊理想和(素)理想之间的关系, 并研究了模糊理想之集的性质； 文献[3]给出了m-半格矩阵M-P广义逆的定义, 得到了m-半格矩阵存在M-P广义逆的一些等价刻画; 文献[4-7]在多种格序结构中研究了滤子的拓扑性质； 文献[8]通过在Quantale中引入滤子的概念, 讨论了Quantale中滤子的拓扑性质, 得到了一系列重要结论. 而m-半格是Quantale的一般化, 基于此, 本文在更广泛的m-半格结构上给出滤子的概念, 研究滤子的若干性质, 构造滤子拓扑并讨论滤子空间的一系列性质.首先, 证明每个滤子空间是连通的且满足第一可数性公理, 并分别给出滤子空间是T0空间和满足第二可数性公理的等价刻画; 其次, 通过在m-半格上引入素滤子的概念, 讨论素滤子与素理想之间的关系, 证明m-半格上的分离引理; 最后, 证明在双侧m-半格上, 其对偶素谱空间是T0的, 并给出其为T1空间的等价刻画.

1 预备知识

定义1[9]设(S,∨)是并半格, (S,·)是半群.若S满足下列条件:

1)S有最大元1;

2) ∀a,b,c∈S,a·(b∨c)=(a·b)∨(a·c), (b∨c)·a=(b·a)∨(c·a).

则称(S,∨,·)是m-半格, 简称S是m-半格.

这里定义的m-半格比文献[1]定义的m-半格更一般化.

定义2[9]设S是m-半格,a∈S.

1) 若a·1≤a, 则称a是S的右侧元;

2) 若1·a≤a, 则称a是S的左侧元;

3) 若a既是右侧元又是左侧元, 则称a是S的双侧元;

4) 若a·a=a, 则称a是S的幂等元.

定义3[9]设S是m-半格.

1) 若S中的每个元都是双侧元, 则称S是双侧m-半格;

2) 若S中的每个元都是幂等元, 则称S是幂等m-半格.

定义4[10]设S1,S2是m-半格,f:S1→S2是映射.若f满足下列条件:

1) ∀a,b∈S1,f(a·b)=f(a)·f(b);

2) ∀a,b∈S1,f(a∨b)=f(a)∨f(b).

则称f是从S1到S2的m-半格同态.

若f是满的, 则称f是m-半格满同态; 若f保最大元, 即f(1S1)=1S2, 则称f是m-半格强同态.

定义5[11]设(X,T )是拓扑空间,A⊆X.如果点x∈X的每个邻域U都有A中异于x的点, 即U∩(A-{x})≠Ø, 则称点x是集合A的凝聚点.集合A所有凝聚点构成的集合称为A的导集, 记作d(A).

定义6[11]设(X,T )是拓扑空间,A⊆X.如果A的每个凝聚点都属于A, 即d(A)⊆A, 则称A是拓扑空间X中的闭集.

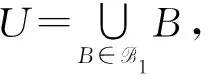
命题1[11]设X是集合, B是X的子集族.如果B满足下列条件:

2) 设B1,B2∈B, 对任意x∈B1∩B2, 存在B∈B, 使得x∈B⊆B1∩B2.

本文中用到而未提及的拓扑与格的概念和性质参见文献[11-12].

2 m-半格中的滤子拓扑

定义8设S是m-半格, Ø≠F⊆S.如果F满足下列条件:

1)F=↑F, 即∀a,b∈S,a≤b,a∈F⟹b∈F;

2)F关于乘法运算·封闭, 即a∈F,b∈F⟹a·b∈F.

则称F是S中的滤子.m-半格S中全体滤子构成的集合记为Fil(S).

例1设S=(0,1].

1) 若·为实数上的乘法运算, 则(S,∨,·)是m-半格.易知{1}是滤子.

2) 若·=∧, 则(S,∨,·)是m-半格.因此, 对任意a∈(0,1], ↑a是滤子.

例2设S=[0,1],c∈[0,1], 定义S上的乘法运算·为

易验证(S,∨,·)是m-半格.取c=0.5, 则可以证明当x>0.25 时, ↑x是滤子.

例3设S={a,b,1},S上的偏序关系≤为

定义S上的乘法运算·为

易验证(S,∨,·)是m-半格, 且↑b是滤子.

命题2设(S,∨,·)是m-半格, 则Fil(S)关于包含序是完备格.

注1设S是m-半格, Ø≠A⊆S, 则∩{F∈Fil(S)|A⊆F}是包含A的最小滤子, 称其为由A生成的滤子, 记为〈A〉F.特别地, 如果A={a}, 则〈{a}〉F简记为〈a〉F.

命题3设S是m-半格, Ø≠A⊆S,a,b∈S,F∈Fil(S), 则:

1) 〈a〉F=∪{↑an|n∈+}; 特别地, 如果a是幂等元, 则 〈a〉F=↑a;

2) 〈A〉F=∪{↑(a1·a2·…·an)|存在n∈+, 使得ai∈A, 1≤i≤n};

若S是双侧的, 则:

4) 〈a〉F∩〈b〉F=〈a∨b〉F;

5) 〈a〉F∨〈b〉F=〈a·b〉F.

证明: 1) 显然∪{↑an|n∈+}是上集.如果x,y∈∪{↑an|n∈+}, 则存在正整数m,n, 使得x≥am,y≥an, 所以x·y≥am·an=am+n, 即x·y∈∪{↑an|n∈+}.因此∪{↑an|n∈+}是含有元素a的滤子.下面说明其为含有元素a的最小滤子.设F是含有元素a的滤子, 由于F对乘法运算·封闭, 所以对任意的正整数n, 有an∈F.又由于F是上集, 所以↑an⊆F, 故

〈a〉F=∪{↑an|n∈+}.

2) 证明方法同1).

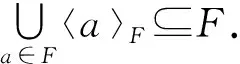
4) 因为〈a〉F,〈b〉F为上集, 所以a∨b∈〈a〉F,a∨b∈〈b〉F, 从而a∨b∈〈a〉F∩〈b〉F, 故〈a∨b〉F⊆〈a〉F∩〈b〉F.另一方面, 对任意的x∈〈a〉F∩〈b〉F, 存在正整数m,n, 使得x≥am,y≥bn.取k=max{m,n}, 由于S是双侧的且乘法·对有限并分配, 所以x≥ak∨bk≥(a∨b)2k, 从而x∈〈a∨b〉F, 于是〈a〉F∩〈b〉F⊆〈a∨b〉F.因此〈a〉F∩〈b〉F=〈a∨b〉F.

5) 因为S双侧, 所以a·b≤a·1≤a,a·b≤1·b≤b, 即a∈〈a·b〉F,b∈〈a·b〉F.故〈a〉F⊆〈a·b〉F, 〈b〉F⊆〈a·b〉F.因此〈a〉F∨〈b〉F⊆〈a·b〉F.另一方面, 由于a∈〈a〉F∨〈b〉F,b∈〈a〉F∨〈b〉F, 所以a·b∈〈a〉F∨〈b〉F, 从而〈a·b〉F⊆〈a〉F∨〈b〉F.因此〈a〉F∨〈b〉F=〈a·b〉F.

注2设S是m-半格, 由命题2可知, Fil(S)是S上某一拓扑的基, 称该拓扑为滤子拓扑, 记为TF.称拓扑空间(S,TF)为滤子空间.

命题4设S是双侧m-半格, 则集族{〈a〉F|a∈S}是滤子空间(S,TF)的一个基.

命题5设S1,S2是m-半格,f:S1→S2是从S1到S2的m-半格强同态, 则S2中的最大元是幂等元当且仅当f-1(1S2)={a∈S1|f(a)=1S2}是S1中的滤子.

证明: 必要性.由于f(1S1)=1S2, 所以1S1∈f-1(1S2), 即f-1(1S2)≠Ø.因为f是保序映射, 所以f-1(1S2)是上集.如果a,b∈f-1(1S2), 则f(a)=f(b)=1S2, 所以

f(a·b)=f(a)·f(b)=1S2·1S2=1S2,

从而a·b∈f-1(1S2).因此f-1(1S2)是S1中的滤子.

充分性.由于f是m-半格强同态, 所以1S1∈f-1(1S2).由于f-1(1S2)是S1中的滤子, 所以1S1·1S1∈f-1(1S2), 从而f(1S1)·f(1S1)=1S2, 即1S2·1S2=1S2.因此S2中的最大元是幂等元.

命题6设S1,S2是m-半格,f:S1→S2是从S1到S2的m-半格强同态,F是S2中的滤子, 则f-1(F)={x∈S1|f(x)∈F}是S1中的滤子.

证明: 因为f(1S1)=1S2且1S2∈F, 所以1S1∈f-1(F), 即f-1(F)≠Ø.设a∈f-1(F),b∈S1且a≤b, 则f(b)≥f(a)∈F.因为F是上集, 所以f(b)∈F, 即b∈f-1(F), 从而f-1(F)是上集.如果a,b∈f-1(F), 则f(a),f(b)∈F, 从而f(a·b)=f(a)·f(b)∈F.于是a·b∈f-1(F), 因此f-1(F)是S1中的滤子.

定理1设S1,S2是m-半格,f:S1→S2是m-半格强同态, 则f关于滤子拓扑是连续映射.

证明: 由命题6知,S2中滤子的原象是S1中的滤子, 所以f关于滤子拓扑是连续映射.

注3设S是m-半格,a∈S, 则{F∈Fil(S)|a∈F}是a在(S,TF)中的一个邻域基, 记为Ua.显然, 〈a〉F是Ua中的最小元.

设A⊆S, 用c(A)和i(A)分别表示A在滤子空间(S,TF)中的闭包与内部.

命题7设S是m-半格,A⊆S, 则:

1)d(A)={x∈S|〈x〉F∩(A{x})≠Ø};

若S是双侧的, 则:

2)c(A)=∩{S〈a〉F|〈a〉F∩A=Ø};

3)i(A)=∪{〈a〉F|〈a〉F⊆A}.

证明: 1) 根据导集的定义,x∈d(A)当且仅当对x的任一邻域U, 均有U∩(A{x})≠Ø.而〈x〉F是Ux中的最小元, 所以对任意的U∈Ux,U∩(A{x})≠Ø当且仅当〈x〉F∩(A{x})≠Ø.因此1)成立.

2)

3)

i(A)= ∪{F|F⊆A,F∈TF}= ∪{F|F⊆A,F∈Fil(S)}= ∪{〈a〉F|a∈S,〈a〉F⊆A}.

推论1设S是m-半格, 1是幂等元,A⊆S, 则1∉d(A).若A∈Fil(S)且1≠x∈A, 则x∈d(A).

命题8设S是m-半格,A⊆S, 则A是闭集当且仅当∀x∉A, 有〈x〉F∩A=Ø.

证明: 必要性.设A是闭集, 则d(A)⊆A.于是∀x∉A, 有x∉d(A), 所以由命题7中1)可知, 〈x〉F∩A=〈x〉F∩(A{x})=Ø.

充分性.设x∈d(A), 由命题7中1)可知, 〈x〉F∩(A{x})≠Ø.于是〈x〉F∩A≠Ø.假设x∉A, 则〈x〉F∩A=Ø, 这与〈x〉F∩A≠Ø矛盾, 所以x∈A.从而d(A)⊆A, 因此A是闭集.

注4设S是m-半格, 则∀a,b∈S,a·b是{a,b}的下确界当且仅当S是双侧幂等的.

定理2设S是双侧m-半格, 则(S,TF)是T0空间当且仅当∀a,b∈S,a·b是{a,b}的下确界.

证明: 必要性.设(S,TF)是T0空间, 要证∀a,b∈S,a·b是{a,b}的下确界, 只需证明S是幂等的.假设存在x∈S不是幂等元, 即x≠x2.由命题3中1)可知,x2∈〈x〉F.因为S是双侧的, 所以x2=x·x≤x, 从而〈x〉F⊆〈x2〉F, 即x∈〈x2〉F.∀U∈Ux, 因为x2∈〈x〉F⊆U∈Ux, 所以U∈Ux2.∀V∈Ux2, 因为x∈〈x2〉F⊆V∈Ux2, 所以V∈Ux.于是Ux=Ux2, 这与(S,TF)是T0空间矛盾.因此x是幂等元, 即S是幂等的.

充分性.设x,y∈S,x≠y.假设Ux=Uy, 由已知条件可知S是幂等的, 则〈x〉F=↑x, 〈y〉F=↑y.因此x≤y且y≤x, 从而x=y, 这与x≠y矛盾.于是Ux≠Uy, 从而(S,TF)是T0空间.

命题9设S是m-半格, |S|≥2, 则滤子空间(S,TF)不是T1空间.

证明: 因为|S|≥2, 所以S{1}≠Ø且S{1}不是开集, 故{1}不是闭集.因此(S,TF)不是T1空间.

定理3设S是m-半格, 则滤子空间(S,TF)是连通空间.若S有最小元, 则(S,TF)是紧的.

证明: 假设存在既开又闭的非空真子集A⊆S.因为A是闭集, 故由命题8可知, ∀x∉A, 有〈x〉F∩A=Ø.由于A是开集, 所以1∈A.于是1∈〈x〉F∩A, 这与〈x〉F∩A=Ø矛盾.因此, (S,TF)中不存在既开又闭的非空真子集, 从而(S,TF)是连通空间.

定理4设S是双侧m-半格, 则:

1) (S,TF)满足第一可数性公理;

2) (S,TF)满足第二可数性公理当且仅当集族{〈a〉F|a∈S}是可数的.

证明: 1) ∀a∈S, 由于〈a〉F是Ua中的最小元, 所以{〈a〉F}⊆Ua是a的一个可数邻域基.因此(S,TF)满足第一可数性公理.

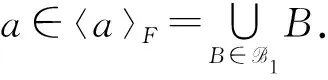
充分性.设集族{〈a〉F|a∈S}是可数的, 由于{〈a〉F|a∈S}是(S,TF)的一个基, 所以(S,TF)满足第二可数性公理.

3 m-半格上的对偶素谱

定义9设S是m-半格,F∈Fil(S),F≠S.若∀a,b∈S,a∨b∈F⟹a∈F或b∈F, 则称F是S中的素滤子.S中全体素滤子构成的集合记为DspecS.

例4可以验证例1～例3中的滤子均为素滤子.

定义10设S是m-半格,I是S的非空真子集.若I满足下列条件:

1)I=↓I, 即∀a,b∈S,a≤b,b∈I⟹a∈I;

2)a∈I,b∈I⟹a∨b∈I;

3) ∀a,b∈S,a·b∈I⟹a∈I或b∈I.

则称I是S中的素理想.

命题10设S是m-半格, Ø≠F⊆S, 则F是S中的素滤子当且仅当SF是S中的素理想.

证明: 必要性.设F是S的素滤子, 且a∈SF,b≤a, 则a∉F.因为F是上集, 所以b∉F.于是SF为下集.如果a,b∈SF, 则a,b∉F.若a∨b∈F, 则a∈F或b∈F, 与a,b∉F矛盾.故a∨b∉F, 从而SF是S的理想.设a·b∈SF, 假设a∈F且b∈F, 则由F是滤子可知a·b∈F, 与a·b∉F矛盾.故a∉F或b∉F, 即a∈SF或b∈SF.因此SF是S的素理想.

充分性.设SF是S的素理想, 且a∈F,a≤b, 则a∉SF.因为SF是下集, 所以b∉SF.于是F为上集.设a,b∈F, 则a∉SF,b∉SF.假设a·b∈SF, 则a∈SF或b∈SF, 与a,b∉SF矛盾.于是a·b∉SF.因此F是S中的滤子.设a,b∈S,a∨b∈F, 若a∈SF且b∈SF, 则由SF是理想得a∨b∈SF, 与a∨b∉SF矛盾.故a∉SF或b∉SF, 即a∈F或b∈F.因此F是S中的素滤子.

命题11设S1,S2是m-半格,f:S1→S2是m-半格满同态.若F是S2中的素滤子, 则f-1(F)={x∈S1|f(x)∈F}是S1中的素滤子.

证明: 由命题6可知,f-1(F)是S1的滤子.设a,b∈S1且a∨b∈f-1(F), 则f(a∨b)∈F, 所以f(a)∨f(b)∈F.由于F是S2中的素滤子, 所以f(a)∈F或f(b)∈F, 从而a∈f-1(F)或b∈f-1(F).因为f是满同态, 所以f-1(F)≠S1.因此f-1(F)是S1中的素滤子.

推论2设S1,S2是m-半格,f:S1→S2是m-半格满同态.如果1S2是S2中的幂等元, 且{1S2}是S2中的素滤子, 则f-1(1S2)是S1中的素滤子.

定理5(m-半格上的分离引理) 设S是双侧m-半格,F∈Fil(S),F≠S.如果I是S中的理想且I∩F=Ø, 则存在S中的素滤子P, 使得I∩P=Ø且F⊆P.

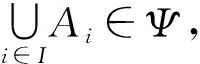
下证P是素滤子.∀x,y∈S且x∨y∈P, 假设x∉P且y∉P, 则〈P∪{x}〉F,〈P∪{y}〉F均真包含P.又因为P是极大元, 于是

I∩〈P∪{x}〉F≠Ø,I∩〈P∪{y}〉F≠Ø.

从而存在z1,z2∈S, 使得z1∈I∩〈P∪{x}〉F,z2∈I∩〈P∪{y}〉F.由命题3中2)可知, 不失一般性, 存在p1,p2,p3,p4∈P, 使得z1≥p1·x·p2,z2≥p3·y·p4.于是

z1∨z2≥(p1·x·p2)∨(p3·y·p4).

由于S是双侧m-半格, 所以

因为p1·p3∈P,x∨y∈P,p2·p4∈P, 所以(p1·p3)·(x∨y)·(p2·p4)∈P.由于P是滤子, 所以z1∨z2∈P.但z1∨z2∈I, 故z1∨z2∈I∩P, 与I∩P=Ø矛盾.因此x∈P或y∈P, 从而P是素滤子.

推论3设S是双侧m-半格, 则:

1) 若F∈Fil(S)且a∈SF, 则存在素滤子P, 使得a∉P且F⊆P;

2) 若1·1=1且1≠a∈S, 则存在素滤子P, 使得a∉P;

3)F∈Fil(S),F≠S, 则F=∩{P∈Fil(S)|F⊆P且P是素的}.

证明: 1) 设F∈Fil(S), 且a∈SF, 则↓a是S中的理想, 且↓a∩F=Ø.于是由定理5可知, 存在素滤子P, 使得↓a∩P=Ø且F⊆P, 即a∉P且F⊆P.

2) 若1·1=1, 则{1}是滤子.由a≠1可知,a∉{1}, 从而存在素滤子P, 使得↓a∩P=Ø且{1}⊆P, 即a∉P.

3)F⊆∩{P∈Fil(S)|F⊆P且P是素的}显然成立.∀x∈∩{P∈Fil(S)|F⊆P且P是素的}, 假设x∉F, 则x∈SF.于是由1)可知, 存在素滤子T, 使得x∉T且F⊆T.因为T是素滤子且F⊆T, 所以x∈T, 与x∉T矛盾.从而x∈F, 进而F⊇∩{P∈Fil(S)|F⊆P且P是素的}.故F=∩{P∈Fil(S)|F⊆P且P是素的}.

设S是m-半格,a∈S, 记

Ua={P∈DspecS|a∉P}, B={Ua|a∈S}.

若A⊆S, 记UA={P∈DspecS|AP}.

命题12设S是m-半格,a,b∈S,F,F1,F2∈Fil(S), {Fλ}λ∈Λ⊆Fil(S), 则:

1)U〈a〉F=Ua;

2)UF1∩UF2=UF1∩F2;

4)Ua∩Ub=Ua∨b;

若S是双侧的, 则:

5)Ua∪Ub=Ua·b.

证明: 1) ∀P∈DspecS, 〈a〉FP当且仅当a∉P, 因此U〈a〉F=Ua.

2) 首先, 设P∈UF1∩UF2, 则P∈UF1且P∈UF2.故F1P且F2P.于是存在x∈F1,y∈F2, 使得x∉P,y∉P, 从而x∨y∈F1∩F2.由于x∨y∉P, 所以F1∩F2P.从而P∈UF1∩F2, 于是UF1∩UF2⊆UF1∩F2.

其次, 设P∈UF1∩F2, 则F1∩F2P, 即F1P且F2P.从而P∈UF1且P∈UF2, 进而P∈UF1∩UF2, 故UF1∩UF2⊇UF1∩F2.于是UF1∩UF2=UF1∩F2.

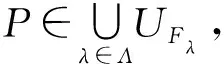
4)P∈Ua∩Ub当且仅当P∈Ua,P∈Ub当且仅当P∈DspecS且a∉P,b∉P当且仅当P∈DspecS且a∨b∉P当且仅当P∈Ua∨b.

5) 由S是双侧的可知,P∈Ua∪Ub当且仅当P∈DspecS且a∉P或b∉P当且仅当P∈DspecS且a·b∉P当且仅当P∈Ua·b.

引理1设S是双侧m-半格,F∈Fil(S),a∈S, 则a∈F当且仅当Ua⊆UF.

证明: 必要性.∀P∈Ua, 有a∉P.由于a∈F, 所以FP.从而P∈UF, 进而Ua⊆UF.

充分性.设Ua⊆UF.假设a∉F, 则由推论3中1)可知, 存在素滤子P, 使得a∉P且F⊆P, 即P∈Ua且P∉UF, 与Ua⊆UF矛盾.因此a∈F.

设S是m-半格, 由推论4和命题12可知, B是DspecS上某一拓扑的一个基.记由基B生成的拓扑为TD, (DspecS,TD)称为S上的对偶素谱空间.

定理6设S是双侧m-半格,F∈Fil(S), 则UF是对偶素谱空间(DspecS,TD)中的开集.反之, ∀V∈TD, 存在S中唯一的滤子F, 使得V=UF.

故UF是(DspecS,TD)中的开集.

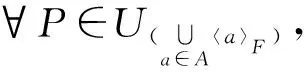
假设存在两个滤子F1,F2, 使得V=UF1=UF2, 则由引理1可知,

a∈F1⟺Ua⊆UF1=UF2⟺a∈F2,

从而F1=F2.因此存在唯一的滤子F使得V=UF.

定理7设S是双侧m-半格,P∈DspecS, 则DspecSUP是{P}在(DspecS,TD)中的闭包.

证明: 因为P∉UP, 所以P∈DspecSUP.由于DspecSUP是闭集, 所以DspecSUP是包含{P}的闭集.设Ψ是(DspecS,TD)中的闭集, 且P∈Ψ.下证DspecSUP⊆Ψ.∀A∈DspecSUP, 有A∉UP, 从而P⊆A.假设A∉Ψ, 则A∈DspecSΨ.由于DspecSΨ是开集, 所以由定理6可知, 存在滤子F, 使得DspecSΨ=UF, 于是FA.故FP, 从而P∈DspecSΨ, 与P∈Ψ矛盾.因此A∈Ψ, 于是DspecSUP是{P}在(DspecS,TD)中的闭包.

定理8设S是双侧m-半格, 则S上的对偶素谱空间(DspecS,TD)是T0空间.

证明: ∀P,Q∈DspecS且P≠Q, 由引理1可知,UP≠UQ.由定理7可知, {P}和{Q}在(DspecS,TD)中的闭包不同, 故(DspecS,TD)是T0空间.

定理9设S是双侧m-半格, 则S上的对偶素谱空间(DspecS,TD)是T1空间当且仅当∀P,Q∈DspecS,P≠Q⟹PQ≠Ø.

证明: 必要性.设(DspecS,TD)是T1空间, 则{P}=DspecSUP, 从而UP=DspecS{P}.因此Q∈UP, 故PQ≠Ø.

充分性.∀P∈DspecS, 显然{P}⊆DspecSUP.∀Q∈DspecSUP, 有Q∉UP, 即P⊆Q.假设P≠Q, 则由已知可知QP≠Ø, 与P⊆Q矛盾.因此Q=P, 于是{P}=DspecSUP是闭集, 从而(DspecS,TD)是T1空间.

定理10设S是m-半格, 若{〈a〉F|a∈S}是一个可数集, 则S上的对偶素谱空间(DspecS,TD)满足第二可数性公理.

证明: 如果{〈a〉F|a∈S}是一个可数集, 则{U〈a〉F|a∈S}是一个可数集.因为U〈a〉F=Ua, 所以{Ua|a∈S}是一个可数集.由于{Ua|a∈S}是对偶素谱空间(DspecS,TD)的基, 所以对偶素谱空间(DspecS,TD)满足第二可数性公理.

定理11设S1,S2是m-半格,f:S1→S2是m-半格满同态, 则f-1: (DspecS2,TD)→(DspecS1,TD)是连续映射.

证明: 由命题11可知,f-1是良定的.下证映射f-1是连续的.∀a∈S1,P∈DspecS2, 有

P∈(f-1)-1(Ua)⟺f-1(P)∈Ua⟺a∉f-1(P)⟺f(a)∉P⟺P∈Uf(a).

故(f-1)-1(Ua)=Uf(a), 因此f-1: (DspecS2,TD)→(DspecS1,TD)是连续映射.

用S表示以双侧m-半格为对象, 以m-半格满同态为态射构成的范畴.用Top0表示以T0拓扑空间为对象, 以连续映射为态射构成的范畴.若S是双侧m-半格, 则DspecS(S)=(DspecS,TD)∈Ob(Top0).若f是m-半格满同态, 则DspecS(f)=f-1是连续映射.

定理12Dspec: Sop→Top0是函子.

从而Dspec(ids)=idDspecS, 故函子Dspec保单位.下证函子Dspec保复合.∀f∈hom(S1,S2),g∈hom(S2,S3), 有

DspecS(g∘opf)=(f∘g)-1=g-1∘f-1=DspecS(g)∘DspecS(f).

故函子Dspec保复合.因此Dspec: Sop→Top0是函子.

综上所述, 本文通过在m-半格中引入滤子的概念, 讨论了m-半格中滤子的若干性质, 进而研究了滤子空间的性质.并在m-半格上定义素滤子的概念, 讨论了素滤子与素理想之间的关系, 得到了m-半格上的分离引理, 给出了m-半格上对偶素谱空间的性质.